Este sitio web se desarrolló para compartir los contenidos creados para dictar semi-presencialmente la materia Álgebra y Geometría Analítica en UTN-FRBA.
El trabajo de producir de ese contenido llevó un poco más de dos años. Después continuamos realizando videos, mejorando explicaciones, agregando ejemplos, parciales resueltos, etc.
Al ponerlos accesibles en la web, los van a poder aprovechar muchos más estudiantes.
El contenido tiene GIFs, videos, applets interactivos con GeoGebra, etc…
Cómo navegar el contenido
Desde el menú superior pueden navegar por los temas separados en unidades:
Las ecuaciones son objetos reutilizables
Las ecuaciones de este material no son imágenes, sino objetos-ecuación creados utilizando MathJax: tipografía matemática de alta calidad, modular, accesible y reutilizable.
Por ejemplo la siguiente matriz está creada usando MathJax:
\[A = \left( {\begin{array}{*{20}{c}}\color{red}{1}&0&2\\1&1&1\\0&3&4\end{array}} \right)\]
Cómo reutilizar las ecuaciones en Word
Al hacer clic derecho sobre una ecuación se abre un menú con opciones. Eligiendo Show Math As > Math ML Code:
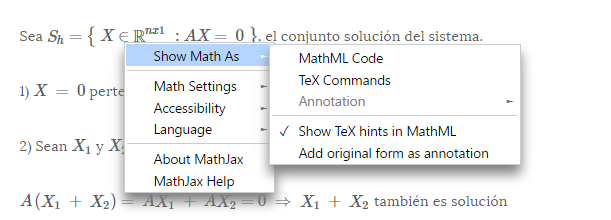
Se obtiene el código en Math ML de la ecuación.
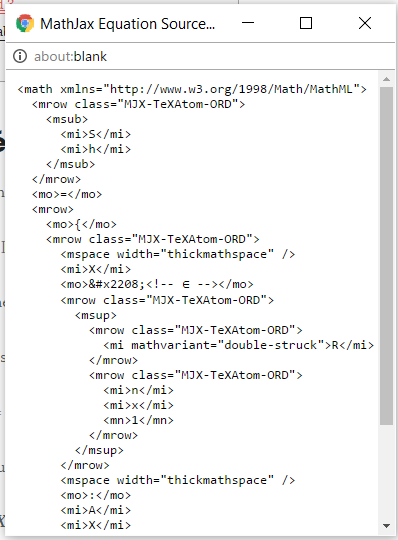
Copiando este código y pegándolo en Word con la opción de pegado Conservar Solo Texto:
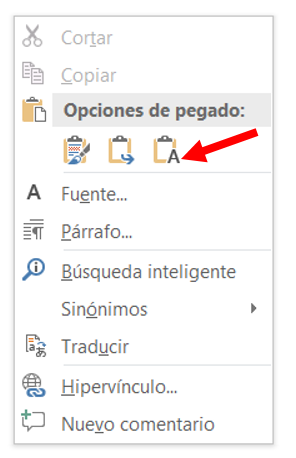
Se obtiene la ecuación no cómo imagen sino cómo objeto editable:
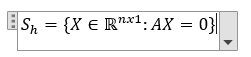
Esta página está en continuo proceso de revisión y actualización para mejorar la experiencia.
Realizado en UTN FRBA


