Circunferencia

Todos conocen las circunferencias, saben que pueden trazarse con un compás.

Les resultará natural la siguiente definición:

\[Centro:C\left( {\alpha ,\beta } \right)\]

\[\mathcal{C} = \left\{ {P\left( {x,y} \right){\rm{|}}d\left( {P,C} \right) = r\;;\;r > 0} \right\}\]

Ahora vamos a deducir partiendo de esta definición, cuál es la expresión de una circunferencia.

Consideremos el siguiente esquema:

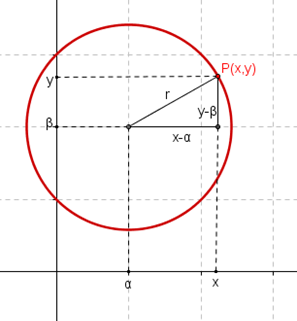
Por teorema de Pitágoras sabemos que los puntos \(P\left( {x,y} \right)\) deben cumplir esta ecuación:

Que se llama ecuación ordinaria de la circunferencia con centro \(C\left( {\alpha ,\beta } \right)\) y radio \(r\).

Si \(r = 0\) , ¿qué objeto geométrico representa la ecuación?

Ecuación canónica de la circunferencia

Hay un caso particular de circunferencia, que tiene su centro en el origen. La ecuación que la define se llama ecuación canónica de la circunferencia:

\[{x^2} + {y^2} = {r^2}\]

Si la circunferencia no está centrada en el \(\left( {0,0} \right)\), es posible armar un nuevo sistema de modo tal que el centro de la circunferencia coincida con el nuevo origen de coordenadas. Por ejemplo consideremos:

\[{\left( {x – \alpha } \right)^2} + {\left( {y – \beta } \right)^2} = {r^2}\]

Si hacemos un cambio de variables:

\[\left\{ {\begin{array}{*{20}{c}}{x’ = x – \alpha }\\{y’ = y – \beta }\end{array}} \right.\]

En las nuevas variables la ecuación queda expresada en forma canónica:

\[{x’^2} + {y’^2} = {r^2}\]

Para obtener la ecuación canónica, hicimos una traslación de ejes, de modo que el centro del nuevo sistema coincidiera con el centro de la circunferencia:

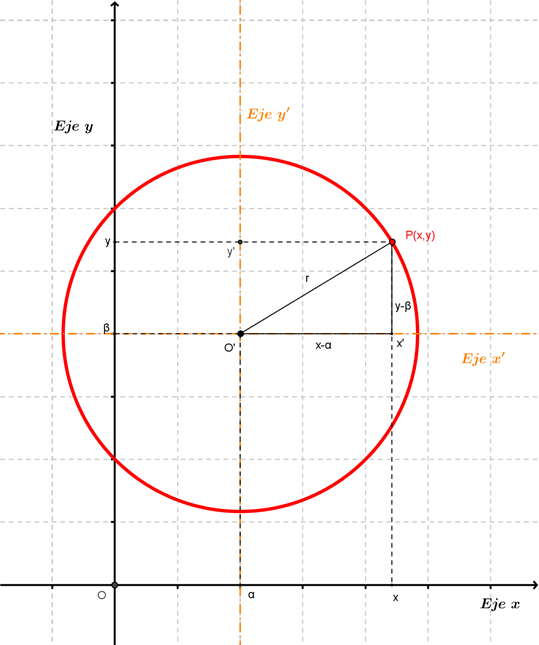
Ejemplo

Encuentre la ecuación de una circunferencia si los extremos de uno de sus diámetros son \(P\left( {4, – 3} \right)\) y \(Q\left( { – 2,7} \right)\).

Conociendo los extremos de un diámetro, ¿cómo obtendrían el centro? ¿Y el radio?

Resolución

Como el segmento \(PQ\) es un diámetro, el centro es el punto medio de este segmento. Y el radio es la mitad de la distancia entre \(P\;y\;Q\):

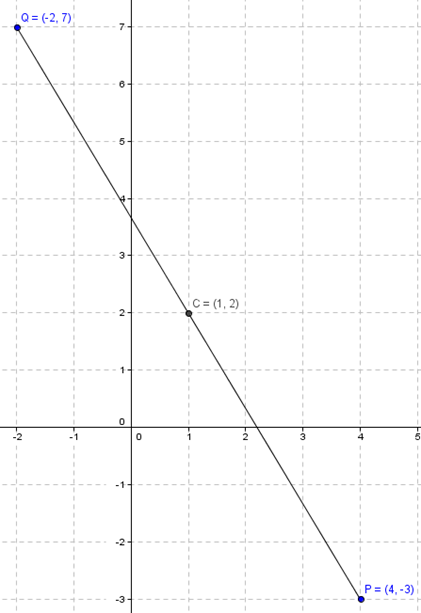
\[C = \left( {\frac{{4 + \left( { – 2} \right)}}{2},\frac{{ – 3 + 7}}{2}} \right) = \left( {1,2} \right)\]

\[\overrightarrow {PQ} = \left( { – 6,10} \right)\; \Rightarrow \;\overrightarrow {PQ} = 2\sqrt {34} \]

\[radio = \sqrt {34} \]

Entonces ya tenemos las coordenadas del centro, y tenemos el radio. Basta con reemplazar en la ecuación ordinaria para obtener la ecuación de esta circunferencia:

\[{\left( {x – 1} \right)^2} + {\left( {y – 2} \right)^2} = 34\]

La gráfica es:

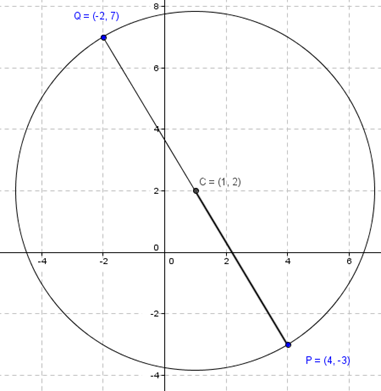
Desde ecuación ordinaria hacia ecuación general

A partir de la ecuación ordinaria de la circunferencia, desarrollemos los cuadrados de binomio:

\[{\left( {x – \alpha } \right)^2} + {\left( {y – \beta } \right)^2} = {r^2}\; \Rightarrow {x^2} – 2\alpha x + {\alpha ^2} + {y^2} – 2\beta y + {\beta ^2} = {r^2}\]

Y ahora reagrupemos los términos:

\[{x^2} + {y^2} – 2\alpha x – 2\beta y + \left( {{\alpha ^2} + {\beta ^2} – {r^2}} \right) = 0\]

Y renombremos las constantes:

Se obtiene la ecuación:

llamada ecuación general de la circunferencia.

Desde ecuación general a ecuación ordinaria

Hemos obtenido a partir de la ecuación ordinaria, la ecuación general de una circunferencia.

Pero dada una ecuación que tiene este aspecto:

\[{x^2} + {y^2} + Dx + Ey + F = 0\]

Si se la pasa a la forma de ecuación ordinaria: ¿siempre se obtendrá una circunferencia?

Para responder esto vamos a recordar cómo se completa cuadrados con un ejemplo.

Ejemplo

Vamos a completar cuadrados en la siguiente expresión:
\[{x^2} + {y^2} – 4x + 2y – 1 = 0\;\;\;\;\;\;\left[ 1 \right]\]

La pregunta es: ¿qué lugar geométrico representa esta ecuación? ¿Estamos seguros de que es una circunferencia? Tendremos que llevarla a la forma ordinaria.

La idea es transformar:

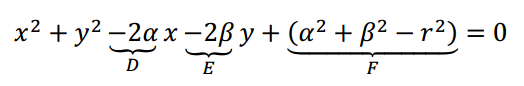
Y además:

Empecemos con \({x^2} – 4x\)

¿Qué le falta a esta expresión para ser un trinomio cuadrado perfecto? Falta el término independiente. Sabemos que el término independiente deberá ser la mitad de 4, elevado al cuadrado.

Entonces podemos sumar y restar \({2^2}\):

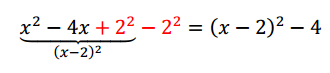
Ahora con la expresión para la variable \(y\):

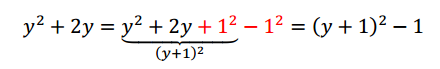
Reemplazamos en la \(\left[ 1 \right]\):

\[{\left( {x – 2} \right)^2} – 4 + {\left( {y + 1} \right)^2} – 1 – 1 = 0\]

Y ahora reordenamos para obtener la ecuación de la circunferencia:

\[{\left( {x – 2} \right)^2} + {\left( {y + 1} \right)^2} = 6\]

¿Cuáles son el centro y el radio?

\[C = \left( {2, – 1} \right)\]

\[r = \sqrt 6 \]

Ejercicio para el lector 1

Completando cuadrados, hallen el lugar geométrico correspondiente a cada una de las ecuaciones:
a)   \({x^2} + {y^2} + 3x + 4 = 0\)

b)   \({x^2} + {y^2} + 6x + 9 = 0\)

Resumen

De la resolución de los puntos anteriores se desprende la conclusión que presentamos a continuación:

Videos relacionados