Composición de transformaciones lineales
Sean \(F\) y \(G\) dos transformaciones lineales tales que: \[F:U \to V{\rm{\;\;\;}};{\rm{\;\;\;\;\;}}G:V \to W\]
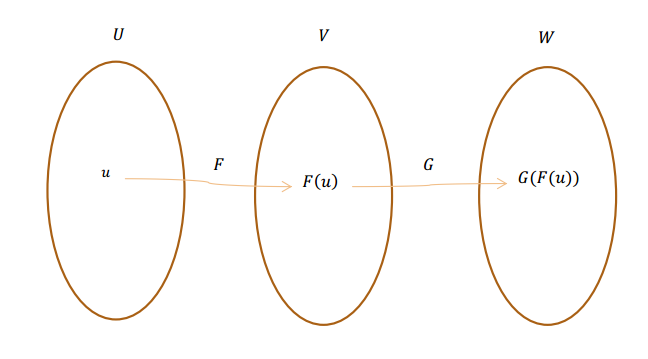
\[\exists GoF:U \to W{\rm{\;}}|{\rm{\;}}GoF\left( u \right) = G\left( {F\left( u \right)} \right){\rm{\;\;}}\forall u \in U\] Propiedad: la composición de transformaciones lineales, es una transformación lineal.
Ejemplo
\[F:{\mathbb{R}^2} \to {\mathbb{R}^3}{\rm{\;}}|{\rm{\;}}F\left( {\left( {x,y} \right)} \right) = \left( {x – y,x + y,2x} \right){\rm{\;\;}}TL\] \[G:{\mathbb{R}^3} \to {\mathbb{R}^2}{\rm{\;}}|{\rm{\;}}G\left( {\left( {x,y,z} \right)} \right) = \left( {x – z,{\rm{\;}}y + z} \right)f{\rm{\;\;}}TL\] Hallar la fórmula de \(GoF\) y \(FoG\), indicando en cada caso dominio y codominio. \[GoF:{\mathbb{R}^2} \to {\mathbb{R}^2},{\rm{\;\;\;}}GoF\left( {\left( {x,y} \right)} \right) = G\left( {\left( {x – y,x + y,2x} \right)} \right)\] \[ = \left( {x – y – \left( {2x} \right){\rm{\;}},{\rm{\;\;\;}}x + y + 2x} \right) = \left( { – x – y,{\rm{\;}}3x + y} \right)\] \[FoG:{\mathbb{R}^3} \to {\mathbb{R}^3}{\rm{\;\;}},{\rm{\;}}FoG\left( {\left( {x,y,z} \right)} \right) = F\left( {\left( {x – z,y + z} \right)} \right)\] \[ = \left( {x – z – \left( {y + z} \right),{\rm{\;}}x – z + \left( {y + z} \right),2x – 2z} \right) = \left( {x – y – 2z,x + y,2x – 2z} \right)\] ¿Con qué operación de matrices se relaciona la composición de transformaciones lineales?
Busquemos las matrices estándar: \[M\left( F \right) \in {\mathbb{R}^{3 \times 2}},{\rm{\;\;}}M\left( F \right) = \left( {\begin{array}{*{20}{c}}1&{ – 1}\\1&1\\2&0\end{array}} \right)\] \[M\left( G \right) \in {\mathbb{R}^{2 \times 3}},{\rm{\;\;\;\;\;}}M\left( G \right) = \left( {\begin{array}{*{20}{c}}1&0&{ – 1}\\0&1&1\end{array}} \right)\] Recuerden que cuando no colocamos subíndices, significa que es la matriz estándar, referida a las bases canónicas.
Calculemos los productos: \[M\left( F \right).M\left( G \right) = \left( {\begin{array}{*{20}{c}}1&{ – 1}\\1&1\\2&0\end{array}} \right)\left( {\begin{array}{*{20}{c}}1&0&{ – 1}\\0&1&1\end{array}} \right) = \left( {\begin{array}{*{20}{c}}1&{ – 1}&{ – 2}\\1&1&0\\2&0&{ – 2}\end{array}} \right)\] Y \[M\left( G \right).M\left( F \right) = \left( {\begin{array}{*{20}{c}}1&0&{ – 1}\\0&1&1\end{array}} \right)\left( {\begin{array}{*{20}{c}}1&{ – 1}\\1&1\\2&0\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{ – 1}&{ – 1}\\3&1\end{array}} \right)\] Ahora hallemos la matriz de \(GoF\) y la matriz de \(FoG\;\)a partir de las respectivas fórmulas: \[M\left( {FoG} \right) = \left( {\begin{array}{*{20}{c}}1&{ – 1}&{ – 2}\\1&1&0\\2&0&{ – 2}\end{array}} \right)\] \[M\left( {GoF} \right) = \left( {\begin{array}{*{20}{c}}{ – 1}&{ – 1}\\3&1\end{array}} \right)\] Entonces hemos comprobado, con un caso particular, que: \[M\left( {GoF} \right) = M\left( G \right).M\left( F \right)\] \[M\left( {FoG} \right) = M\left( F \right).M\left( G \right)\] Es decir que la composición de transformaciones lineales se expresa matricialmente a través de un producto de matrices.
Matriz asociada a la composición de transformaciones lineales
Sean \(F\) y \(G\) dos transformaciones lineales tales que: \[F:U \to V{\rm{\;\;\;}};{\rm{\;\;\;\;\;}}G:V \to W\] Y sean \({B_1},{B_2},{B_3}\) bases de \(U,V\) y \(W\) respectivamente, entonces se puede demostrar que:
Inversa de una transformación lineal
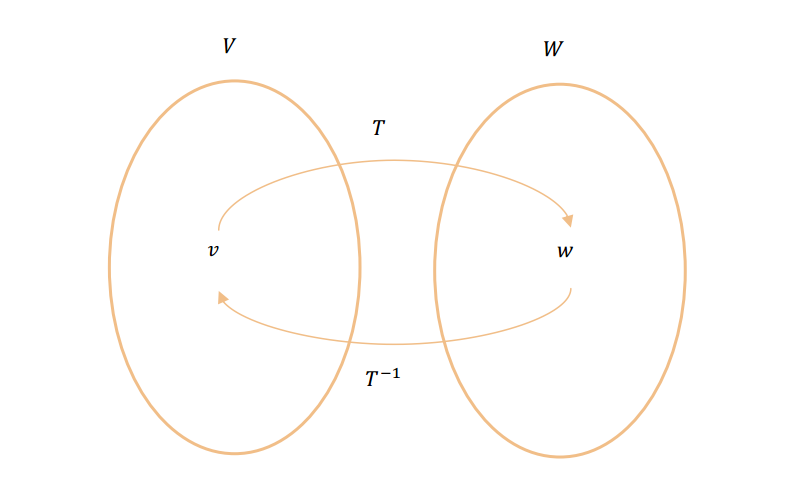
\({T^{ – 1}}\) también es una transformación lineal biyectiva: \[{T^{ – 1}}oT = I{d_V}\] \[To{T^{ – 1}} = I{d_w}\] Observación: Para que exista una transformación lineal biyectiva entre dos espacios vectoriales, éstos deben tener la misma dimensión. ¿Por qué?
Ejemplo
Sea la transformación lineal \(T:{\mathbb{R}^2} \to {\mathbb{P}_1}\), \(T\left( {\left( {a,b} \right)} \right) = a – b + 2ax\)
¿Cuál es el núcleo de \(T\)?
\[a – b + 2ax = 0x + 0 \Rightarrow {\rm{\;}}\left\{ {\begin{array}{*{20}{c}}{a – b = 0}\\{2a = 0}\end{array}{\rm{\;}}} \right. \Rightarrow a = 0 = b\] \[Nu\left( T \right) = \left\{ {\left( {0,0} \right)} \right\}\] ¿Cuál es la imagen de \(T\)? \[T\left( {\left( {1,0} \right)} \right) = 2x + 1\] \[T\left( {\left( {0,1} \right)} \right) = – 1 + 0x\] Estos dos polinomios ¿son LI o LD? Son LI, y por lo tanto la dimensión de la imagen es 2. La imagen ‘vive’ en \({\mathbb{P}_1}\), entonces: \[Im\left( T \right) = {\mathbb{P}_1}\] Comprobamos que \(T\) es un isomorfismo, entonces existe la transformación lineal inversa \[{T^{ – 1}}:{\mathbb{P}_1} \to {\mathbb{R}^2}\] \[T\left( {\left( {1,0} \right)} \right) = 2x + 1\] \[T\left( {\left( {0,1} \right)} \right) = – 1 + 0x\] Entonces: \[{T^{ – 1}}\left( {2x + 1} \right) = \left( {1,0} \right)\] \[{T^{ – 1}}\left( { – 1 + 0x} \right) = \left( {0,1} \right)\] ¿Está bien definida \({T^{ – 1}}\)? Sí, porque \(\left\{ {2x + 1, – 1} \right\}\) es una base de \({P_1}\) (por teorema fundamental de las transformaciones lineales).
Matriz de la transformación inversa
Sea \(T:V \to W\) isomorfismo, \(\dim \left( V \right) = \dim \left( W \right) = n\), y \(M{\left( T \right)_{BB’}} \in {\mathbb{R}^{n \times n}}\) la matriz asociada a T respecto de las bases B y B’.
Recordemos que el rango de la matriz asociada es igual a la dimensión de la imagen.
Como T es isomorfismo, \(Im\;\left( T \right)\; = \;W\) y por lo tanto: (\(rg\left( {M{{\left( T \right)}_{BB’}}} \right) = n\).
Entonces\(\;\;\;M{\left( T \right)_{BB’}}\) es inversible y su inversa es la matriz de \({T^{ – 1}}\) respecto de las bases \(B’\) y \(B\):
En el siguiente esquema se puede observar cómo operan las matrices \(M{\left( T \right)_{BB’}}\) y \(M{\left( {{T^{ – 1}}} \right)_{B’B}}\):
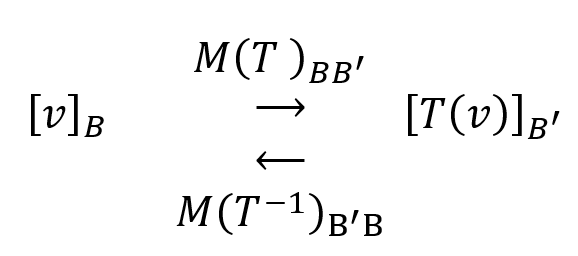
Caso particular: \(V = W = {\mathbb{R}^n}\),
\[A = M{\left( T \right)_{EE}}\;\; \Rightarrow \;\;{A^{ – 1}} = M{\left( {{T^{ – 1}}} \right)_{EE}}\]
Ejemplo
Sea \(T:\;\;{\mathbb{R}^3} \to {\mathbb{R}^3}\) una TL, tal que \(\;T\left( {x,y,z} \right)\; = \;\left( {x + y,\;x – z,\;z} \right)\), hallar la fórmula de \({T^{ – 1}}\).
Resolución
Construyamos la matriz asociada a la TL en las bases canónicas: \[M\left( T \right) = A = \left( {\begin{array}{*{20}{c}}1&1&0\\1&0&{ – 1}\\0&0&1\end{array}} \right)\]
Sabemos que \({A^{ – 1}}\) será la matriz asociada a la TL inversa: \[M\left( {{T^{ – 1}}} \right) = \;{A^{ – 1}} = \left( {\begin{array}{*{20}{c}}0&1&1\\1&{ – 1}&{ – 1}\\0&0&1\end{array}} \right)\]
Y a partir de la matriz estándar de la TL inversa podemos hallar la fórmula de la TL inversa:
\[{T^{ – 1}}:{\mathbb{R}^3} \to {\mathbb{R}^3}\;\;,\;\;\;{T^{ – 1}}\left( {\left( {x,y,z} \right)} \right) = \left( {y + z,x – y – z,z} \right)\]
Ejercicio para el lector 5
Dadas las transformaciones lineales: \(F\) de \({\mathbb{R}^3} \to {\mathbb{R}^2}\) , \(F\left( {x,y,z} \right)\; = \left( {x – y\;,\;y + z} \right)\) y \(G\) de \({\mathbb{R}^2} \to {\mathbb{R}^3}\) , \(G\left( {a,b} \right)\; = \;\left( {a + b\;,\;0,\;2a + kb} \right)\)
a) Determinar todos los valores de \(k\) para los cuales \(F \circ G\) es biyectiva (isomorfismo).
b) Para \(k = 1\), obtener \({\left( {F \circ G} \right)^{ – 1}}\left( {1,0} \right)\).

