Operaciones en forma trigonométrica y exponencial

Módulo y argumento de un número complejo

Sea  \(z\; = \;a\; + \;bi\;\;\;\;\left( {z \ne 0} \right)\)

Habíamos visto que un número complejo puede representarse como un punto del plano. Ese punto tiene asociado un vector que queda unívocamente determinado por su módulo \(\left| z \right|\)  y su argumento \(\theta \) , tal como muestra la figura:

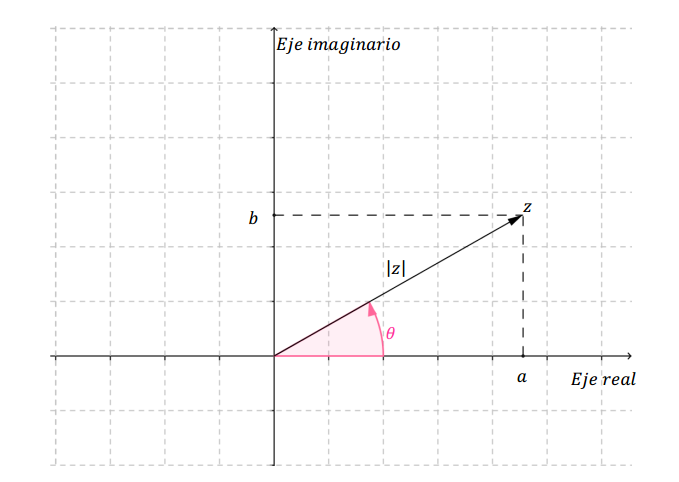
El módulo se calcula como el módulo de un vector en \({\mathbb{R}^2}\):

\[\left| z \right| = \sqrt {{a^2} + {b^2}} \]

Se define  \(\theta  = {\rm{arg}}\left( z \right)\) como el ángulo entre el semieje positivo de abscisas y el vector. El argumento  puede determinarse, teniendo en cuenta los signos de  \(a\)  y  \(b\) con:

\[\;\;\;tg\left( \theta  \right) = \frac{b}{a}{\rm{\;\;}},{\rm{\;\;\;a}} \ne 0{\rm{\;\;}}\]

Ejemplo 1

Sea  \(z =  – 3 + \sqrt 3 i\), hallemos su módulo y su argumento:

\[\left| z \right| = \sqrt {{{\left( { – 3} \right)}^2} + {{\left( {\sqrt 3 } \right)}^2}}  = \sqrt {12} \]

Para hallar el argumento es útil hacer una gráfica aproximada de \(z\):

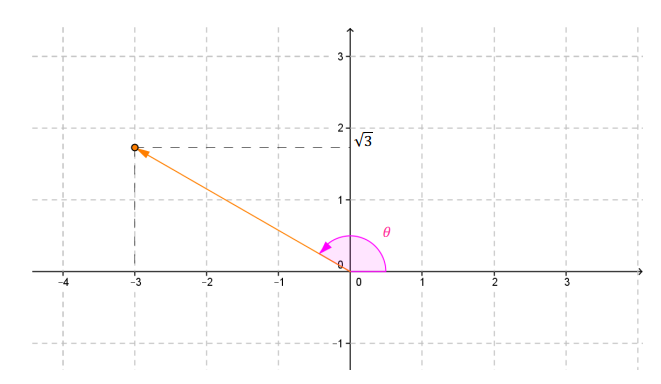
A partir de esta gráfica observamos que \(z\) pertenece al segundo cuadrante.

Para hallar \(\theta \) resolvemos la siguiente ecuación trigonométrica:

\[tg\left( \theta  \right) =  – \frac{{\sqrt 3 }}{3}\]

Como se ha estudiado en el seminario de ingreso, existen infinitos ángulos tales que su tangente es \( – \sqrt 3 /3\). Los cuadrantes en los cuales la tangente es negativa son el segundo y el cuarto.

Usando calculadora o la tabla de senos, cosenos y tangentes de ángulos notables es posible hallar una primera solución:

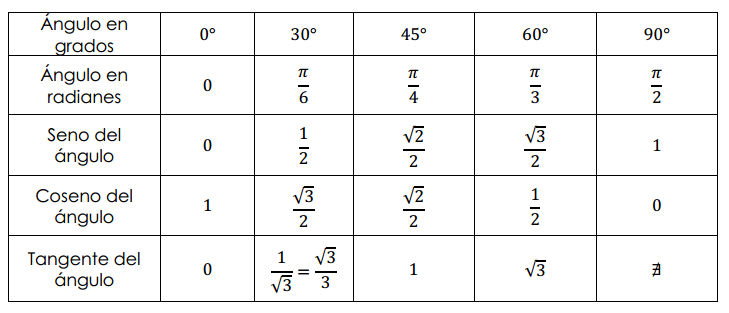
De la tabla vemos que  \(tg\left( {\frac{\pi }{6}} \right) = \frac{{\sqrt 3 }}{{\;3}}\) , luego   \(tg\left( { – \frac{\pi }{6}} \right) =  – \;\frac{{\sqrt 3 }}{{\;3}}\)

Con calculadora usando la función arcotangente se obtiene:

\[ – 0,523598776 \cong  – \frac{\pi }{6} = \theta \]

Hemos hallado una solución en el cuarto cuadrante; para obtener la solución en el segundo cuadrante, sumamos \(\pi \) como muestra la siguiente gráfica:

\[ – \frac{\pi }{6} + \pi  = \frac{5}{6}\pi \]

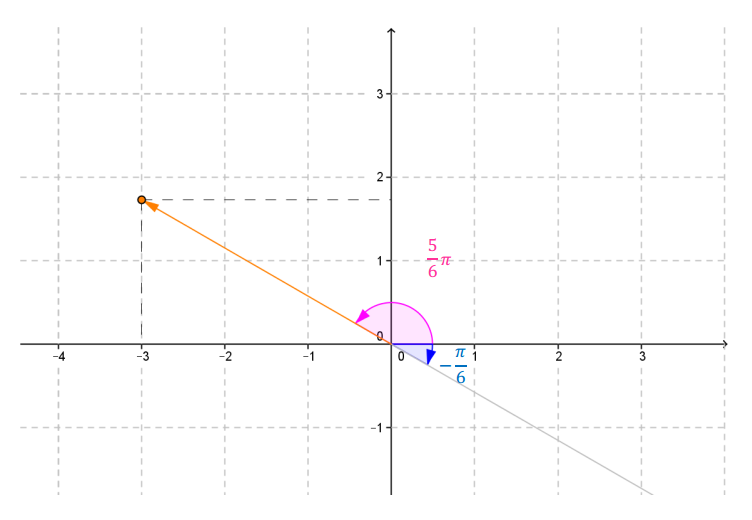
El conjunto de las infinitas soluciones de la ecuación\(tg\left( \theta  \right) =  – \frac{{\sqrt 3 }}{3}\)es:

\[\theta  =  – \frac{\pi }{6} + 2k\pi \;\; \vee \;\;\theta  = \frac{5}{6}\pi  + 2k\pi \;\;\;,\;\;\;k \in \mathbb{Z}\]

Pero, de acuerdo con los signos de \(a\) y \(b\), sabemos que las soluciones del cuarto cuadrante no describen a \(z\).

Entonces resulta:

\[\arg \left( z \right) = \frac{5}{6}\pi  + 2k\pi \;\;\;,\;\;\;k \in \mathbb{Z}\]

De estos infinitos argumentos se llama argumento principal de \(z\), y se anota \(Arg\left( z \right)\), al único comprendido en el intervalo \(\left[ {0,2\pi } \right)\).

Luego el argumento principal de \(z\) es:

\[Arg\left( z \right) = \frac{5}{6}\pi \]

Ejemplo 2

Sea \(z =  – 0,5i\). En este caso \(a = 0\), entonces \(\theta \) no puede determinarse con la fórmula\(tg\left( \theta  \right) = b/a\). Si hacemos un gráfico:

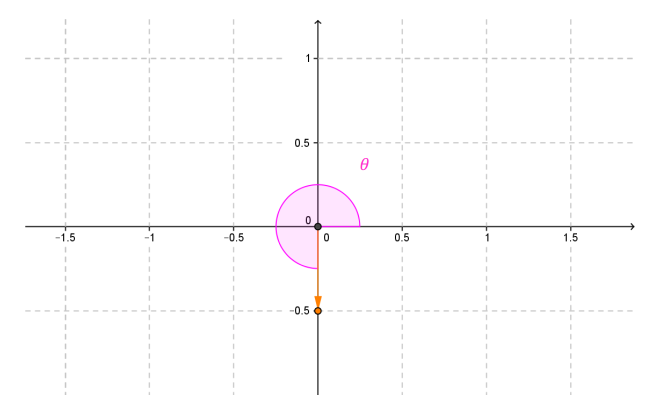
Vemos que el argumento principal de \(z\) es \(3\pi /2\).

 

Generalizando:

Si \(a = 0\), \(z\) es imaginario puro  y su argumento dependerá del signo de  b:

\[a = 0\;\; \wedge \;\;b > 0\;\; \Rightarrow \;\;\;Arg\left( z \right) = \frac{\pi }{2}\]

\[a = 0\;\; \wedge \;\;b < 0\;\; \Rightarrow \;\;\;Arg\left( z \right) = \frac{{3\pi }}{2}\]

Observación: Si  \(z = 0\) ,  \(\left| z \right| = 0\)  pero el argumento no está definido.

Forma trigonométrica o polar de un número complejo

Consideremos la siguiente figura:

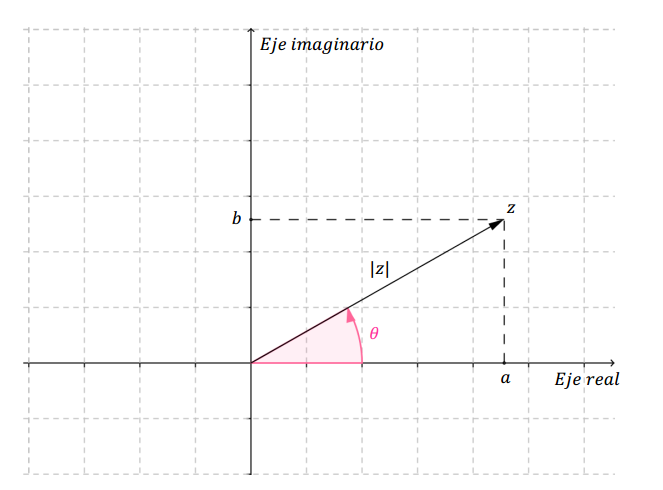
Se deduce que:

\[a = \left| z \right|{\rm{cos}}\left( \theta  \right)\;\;\;\;\;,\;\;\;\;\;b = \left| z \right|\;sen\left( \theta  \right)\]

Entonces resulta:

\[z = a + bi\; = \;\;\left| z \right|\cos \left( \theta  \right) + i\;\left| z \right|\;sen\left( \theta  \right)\]

Por lo tanto:

En algunos textos se usa una abreviatura para la forma trigonométrica:

\[\cos \left( \theta  \right) + i{\rm{sen}}\left( \theta  \right)\;\;\; = \;cis\left( \theta  \right)\]

\[z = \left| z \right|\;cis\left( \theta  \right)\]

Ejemplo

Expresar los siguientes números complejos en forma trigonométrica:

\[{z_1} =  – 3 + \sqrt 3 i\]

\[{z_2} =  – 2\]

\[{z_3} =  – 2 – 2i\]

\[{z_4} =  – 1,5i\]

Resolución

Debemos buscar el módulo y argumento de cada uno de los números complejos.

Para \({z_1}\) ya habíamos averiguado módulo y argumento, luego su forma trigonométrica es:

\[{z_1} = \sqrt {12} .\left( {\cos \frac{5}{6}\pi  + i.sen\frac{5}{6}\pi } \right)\]

Para \({z_2}\) calculemos el módulo:

\[\left| {{z_2}} \right| = \sqrt {{{\left( { – 2} \right)}^2}}  = 2\]

Para hallar el argumento, es muy útil pensar en la gráfica de \({z_2} =  – 2\):

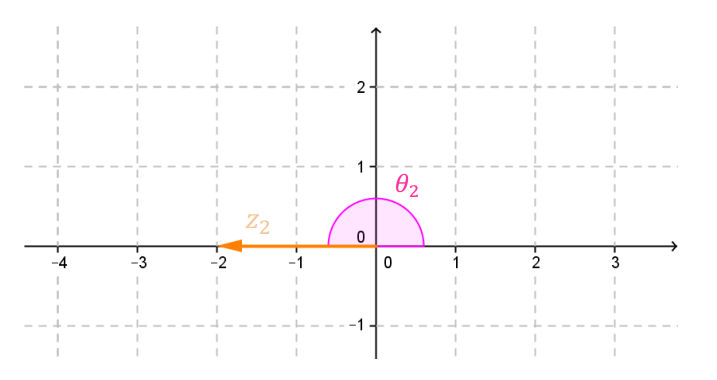
\({z_2}\) está sobre el semieje negativo real, luego el argumento principal es:

\[Arg\left( {{z_2}} \right) = \pi \]

Entonces:

\[{z_2} = 2.\left( {\cos \pi  + i.{\rm{sen}}\pi } \right)\]

Observación:  Para  \({z_2} =  – 2\) , resulta  \(tg\left( {{\theta _2}} \right) = 0\) . La función arcotangente  devuelve  \({\theta _2} = 0\)  pero este argumento no corresponde porque  \({z_2}\)  está sobre el semieje real negativo. Por eso, para hallar el argumento hay que tener presente la ubicación del complejo en el plano.

Para \({z_3} =  – 2 – 2i\), hallamos el módulo:

\[\left| {{z_3}} \right| = \sqrt {{{\left( { – 2} \right)}^2} + {{\left( { – 2} \right)}^2}}  = \sqrt 8 \]

Sabemos por los signos de \(a\) y \(b\)  que está en el tercer cuadrante y que:

\[tg\left( {{\theta _3}} \right) = 1\]

Luego el argumento principal es:

\[Arg\left( {{z_3}} \right) = \frac{5}{4}\pi \]

Entonces:

\[{z_3} = \sqrt 8 .\left( {\cos \frac{5}{4}\pi  + i.sen\frac{5}{4}\pi } \right)\]

Forma exponencial de un número complejo

Existe otra manera de expresar los números complejos conociendo su módulo y su argumento, llamada forma exponencial. Esta expresión se basa en la siguiente fórmula:

Sea  \(\theta  = \arg \left( z \right)\) expresado en radianes. La expresión trigonométrica de \(z\) es:

\[z = \left| z \right|\;(\cos \theta  + i\;sen\theta )\]

Aplicando la fórmula de Euler, resulta:

Ejemplos

\[{z_1}\; = \;3i\; = \;3\left( {\cos \frac{\pi }{2} + i\;sen\frac{\pi }{2}} \right) = 3\;{e^{i\;\frac{\pi }{2}}}\]

\[{z_2} = 1 – i = \sqrt 2 \left( {cos\frac{{7\pi }}{4} + i\;sen\frac{{7\pi }}{4}} \right) = \sqrt {2\;} {e^{i\;\frac{{7\pi }}{4}}}\]

Operaciones en forma exponencial

Puede demostrarse que la exponencial compleja verifica las propiedades básicas de la potenciación, lo cual permite resolver en forma sencilla las operaciones con números complejos.

Si  \({z_1} = \left| {{z_1}} \right|{e^{i\;{\theta _1}}}\)   y   \({z_2} = \left| {{z_2}} \right|{e^{i\;{\theta _2}}}\)  , resulta:

\[{z_{1\;}}{z_2} = \;\left| {{z_1}} \right|{e^{i\;{\theta _1}}}\left| {{z_2}} \right|\;{e^{i\;{\theta _2}}}\]

Por lo tanto:

O sea: para multiplicar números complejos, se multiplican sus módulos y se suman sus argumentos.

Análogamente, para dividir números complejos, se dividen sus módulos y se restan sus argumentos:

Para calcular potencias:

\({z^n} = {\left( {\left| z \right|{e^{i\;\theta }}} \right)^n}\;,\;\;\;\;n \in N\)

Por lo tanto:

Ejemplos

Sean:

\({z_1}\; = \;3i\; = \;3\left( {\cos \frac{\pi }{2} + i\;sen\frac{\pi }{2}} \right) = 3\;{e^{i\;\frac{\pi }{2}}}\)

\({z_2} = 1 – i = \sqrt 2 \left( {cos\frac{{7\pi }}{4} + i\;sen\frac{{7\pi }}{4}} \right) = \sqrt {2\;} {e^{i\;\frac{{7\pi }}{4}}}\)

Resolver las siguientes operaciones en forma exponencial:

a) \({z_1}.{z_2}\)

b) \({z_1}/{z_2}\)

c) \({z_1}^{10}\)

Resolución

Ítem a

\[{z_1}.{z_2} = 3.\sqrt 2 .{e^{\left( {\frac{\pi }{2} + \frac{7}{4}\pi } \right)i}} = 3\sqrt {2\;} {e^{\frac{9}{4}\pi i}}\]

En general suele utilizarse el argumento principal, que está comprendido en \(\left[ {0\;,\;2\pi } \right)\). Teniendo en cuenta que   \(\frac{9}{4}\pi  = 2\pi  + \frac{\pi }{4}\)  , resulta  \(Arg\left( {{z_1}{z_2}} \right) = \frac{\pi }{4}\).

Entonces:

\[{z_1}.{z_2} = 3\sqrt {2\;} {e^{\frac{\pi }{4}i}}\]

Ítem b

\[\frac{{{z_1}}}{{{z_2}}} = \;\frac{3}{{\sqrt 2 }}\;e{\;^{\left( {\frac{\pi }{2}\; – \;\frac{7}{4}\pi } \right)i}} = \frac{3}{{\sqrt 2 }}\;{e^{ – \;\frac{5}{4}\pi i}}\]

\[Arg\left( {\frac{{{z_1}}}{{{z_2}}}} \right) =  – \frac{5}{4}\pi  + 2\pi  = \frac{3}{4}\pi \]

\[\frac{{{z_1}}}{{{z_2}}} = \frac{3}{{\sqrt 2 }}\;e{\;^{\frac{3}{4}\pi i}}\]

Ítem c

\[{z_1}^{10} = {3^{10}}{e^{i\;\frac{\pi }{2}.10}} = {3^{10}}{e^{i\;5\pi }}\]

Buscamos el argumento principal:   \(5\pi  – 2\left( {2\pi } \right) = \pi \)

Queda entonces:

\[{z_1}^{10} = {3^{10}}{e^{i\;\pi }}\]

Identidad de Euler

Como caso particular de la fórmula de Euler, se deduce una de las fórmulas más bellas de la Matemática, conocida como Identidad de Euler:

\[\;\;{e^{i\pi }} + 1 = 0\]

Es notable por relacionar 5 de los números más importantes de la Matemática:

• El 0  y el 1 , neutros respecto de la suma y de la multiplicación.
• El número \(\pi \) que relaciona la longitud de la circunferencia con su diámetro y está presente en varias de las ecuaciones fundamentales de la Física.
• El número de Euler \(e\), que aparece en numerosos procesos naturales y en diferentes problemas físicos y matemáticos.
• La unidad imaginaria \(i\) , base para la construcción del conjunto \(\mathbb{C}\) .

Dejamos a cargo del lector la comprobación de esta identidad.

Operaciones en forma trigonométrica

Traduciendo a la forma trigonométrica los resultados obtenidos, resulta:

\[{z_1}{z_2} = \;\left| {{z_1}} \right|\left| {{z_2}} \right|\left[ {\cos \left( {{\theta _1} + {\theta _2}} \right) + i\;sen\left( {{\theta _1} + {\theta _2}} \right)} \right]\]

\[\frac{{{z_1}}}{{{z_2}}} = \frac{{\left| {{z_1}} \right|}}{{\left| {{z_2}} \right|}}\left[ {\cos \left( {{\theta _1} – {\theta _2}} \right) + i\;sen\left( {{\theta _1} – {\theta _2}} \right)} \right]\]

\[{z^n} = {\left| z \right|^n}\left[ {\cos \left( {n\theta } \right) + i\;sen\left( {n\theta } \right)} \right]\;\;\;,\;\;\;n \in \mathbb{N}\]

NOTA PARA EL LECTOR INTERESADO:

Las fórmulas del producto y del cociente pueden demostrarse a partir de relaciones entre las funciones trigonométricas. Por ejemplo, el producto puede deducirse a partir de las siguientes identidades:

\[\cos \left( {\alpha  + \beta } \right) = \cos \left( \alpha  \right).\cos \left( \beta  \right) – sen\left( \alpha  \right).sen\left( \beta  \right)\;\;\;\;\left[ 1 \right]\]

\[sen\left( {\alpha  + \beta } \right) = sen\left( \alpha  \right).\cos \left( \beta  \right) + \cos \left( \alpha  \right).sen\left( \beta  \right)\;\;\;\;\left[ 2 \right]\]

Sean   \({z_1} = \left| {{z_1}} \right|.\left( {\cos \left( \alpha  \right) + i.sen\left( {\;\alpha } \right)} \right)\) y que \({z_2} = \left| {{z_2}} \right|.\left( {\cos \left( \beta  \right) + i.sen\left( \beta  \right)} \right)\). Queremos calcular el producto:

\[{z_1}.{z_2} = \left| {{z_1}} \right|\left| {{z_2}} \right|.\left( {\cos \left( \alpha  \right) + i.sen\left( {\;\alpha } \right)} \right)\left( {\cos \left( \beta  \right) + i.sen\left( \beta  \right)} \right)\]

\[= \left| {{z_1}} \right|\left| {{z_2}} \right|.\left[ {\cos \left( \alpha  \right).\cos \left( \beta  \right) – sen\left( \alpha  \right).sen\left( \beta  \right) + i.\left( {\cos \left( \alpha  \right).sen\left( \beta  \right) + sen\left( \alpha  \right).\cos \left( \beta  \right)} \right)} \right]\]

Por  [1] y [2]:

\[{z_1}.{z_2} = \left| {{z_1}} \right|\left| {{z_2}} \right|.\left( {\cos \left( {\alpha  + \beta } \right) + i.sen\left( {\;\alpha  + \beta } \right)} \right)\]

Observamos que coincide con lo que habíamos deducido en forma exponencial.

Ejemplo

Sean:

\({z_1} =  – 3 + \sqrt 3 i\)

\({z_2} =  – 2\)

\({z_3} =  – 2 – 2i\)

Calcular usando la forma trigonométrica:

\[\frac{{{z_1}.z_2^3}}{{{z_3}}}\]

Resolución

Calculamos módulo y argumento de cada uno:

\(\left| {{z_1}} \right| = \sqrt {{{\left( { – 3} \right)}^2} + {{\sqrt 3 }^2}}  = \sqrt {12} \)   ;   \(Arg\left( {{z_1}} \right) = \frac{5}{6}\pi  \Rightarrow {z_1} = \sqrt {12} cis\left( {\frac{5}{6}\pi } \right)\)

\(\left| {{z_2}} \right| = \sqrt {{{\left( { – 2} \right)}^2} + {0^2}}  = 2\)   ;   \(Arg\left( {{z_2}} \right) = \pi  \Rightarrow {z_2} = 2cis\left( \pi  \right)\)

\(\left| {{z_3}} \right| = \sqrt {{{\left( { – 2} \right)}^2} + {{\left( { – 2} \right)}^2}}  = \sqrt 8 \)   ;   \(Arg\left( {{z_3}} \right) = \frac{5}{4}\pi  \Rightarrow {z_2} = 2cis\left( \pi  \right)\)

Entonces:

\[\frac{{{z_1}.z_2^3}}{{{z_3}}} = \frac{{\sqrt {12} {{.2}^3}}}{{2\sqrt 2 }}.cis\left( {\frac{5}{6}\pi  + 3\left( \pi  \right) – \frac{5}{4}\pi } \right) = \frac{{8\sqrt 3 }}{{\sqrt 2 }}.cis\left( {\frac{{61}}{{12}}\pi } \right)\]

Si buscamos el argumento principal restando \(4\pi \) de \(\frac{{61}}{{12}}\pi \) obtenemos:

\[ = \frac{{8\sqrt 3 }}{{\sqrt 2 }}.cis\left( {\frac{{13}}{{12}}\pi } \right)\]

Ejercicio para el lector 1

Completar la siguiente tabla: