En las unidades anteriores vimos que el álgebra de vectores y el álgebra de matrices presentan similitudes. Pudimos observar que las propiedades de la suma (de vectores o de matrices) y del producto por un escalar son idénticas en ambos conjuntos.
En esta unidad, generalizaremos el concepto de vector a partir de estas propiedades en común que hemos señalado para vectores geométricos y matrices.
Definición de espacio vectorial
Llamamos \(u\; + \;v\) a la suma de vectores en \(V\), y \(\alpha v\) al producto de un número real \(\alpha \) por un vector \(v\; \in \;V\).
1. \(u + v\;\; \in \;V\)
2. \(u + v = v + u\)
3. \(\left( {u + v} \right) + w = u + \left( {v + w} \right)\)
4. Existe un vector nulo \({0_V} \in V\) tal que \(v + {0_V} = v\)
5. Para cada \(v\) en \(V\), existe un opuesto \(\left( { – v} \right) \in V\) tal que \(v + \left( { – v} \right) = {0_V}\)
6. \(\alpha v\; \in \;V\)
7. \(\alpha \left( {u + v} \right) = \alpha u + \alpha v\)
8. \(\left( {\alpha + \beta } \right)v = \alpha v + \beta v\)
9. \(\alpha \left( {\beta v} \right) = \left( {\alpha \beta } \right)v\)
10. \(1v = v\)
Observación: En la definición anterior, cuando decimos «escalares» nos estamos refiriendo a números reales. En este caso, se dice que \(V\) es un espacio vectorial real.
También es posible que los escalares pertenezcan a otro conjunto numérico, por ejemplo los números complejos con los cuales trabajaremos en la última unidad.
Ejemplo 1
De acuerdo con las propiedades que vimos en la primera unidad, podemos afirmar que \({\mathbb{R}^3}\) es un espacio vectorial.
Los espacios \({\mathbb{R}^n}\) , con \(n \ge 1\) , son los ejemplos principales de espacios vectoriales. La intuición geométrica desarrollada para \({R^3}\) nos ayudará a entender y visualizar muchos conceptos de esta unidad.
Los vectores de \({\mathbb{R}^{\;n}}\) son n-uplas de números reales, o sea:
\[{\mathbb{R}^n} = \left\{ {\left( {{x_1},\;{x_2},\; \ldots ,\;{x_n}} \right)\;,\;\;\;con\;\;{x_i} \in \mathbb{R}} \right\}\]
En \({\mathbb{R}^n}\) , la suma de vectores y el producto por un escalar se definen así:
Sean \(\;\;u = \left( {{u_1},{u_2}, \ldots ,{u_n}} \right)\;\;\;\;y\;\;\;\;v = \left( {{v_1},{v_2}, \ldots {v_n}} \right)\; \in {\mathbb{R}^n}\;\)
\[u + v = \left( {{u_1} + {v_1},\;{u_2} + {v_2},\; \ldots ,\;{u_n} + {v_n}} \right) \in {\mathbb{R}^n}\]
\[\alpha v = \left( {\alpha {v_1},\;\alpha {v_2},\; \ldots ,\;\alpha {v_n}} \right) \in {\mathbb{R}^n}\]
Puede comprobarse que las operaciones definidas verifican los axiomas de espacio vectorial.
Ejemplo 2
De acuerdo con las propiedades enunciadas en la segunda unidad, para cada \(m\) y \(n\) \({\mathbb{R}^{mxn}}\) es un espacio vectorial.
Tenemos por ejemplo \({\mathbb{R}^{2×3}}\), espacio vectorial cuyos vectores son las matrices de \(2 \times 3\).
Ejemplo 3
Llamemos \({P_2}\) al conjunto de polinomios de grado menor o igual que 2, incluyendo el polinomio nulo.
Recordemos la suma de polinomios y la multiplicación por un escalar:
Dados \(p\left( x \right) = \;{a_o} + {a_1}x + {a_2}{x^2} \in {P_2}\) y \(q\left( x \right) = {b_o} + {b_1}x + {b_2}{x^2} \in {P_2}\)
Definimos las operaciones:
\[\left( {p + q} \right)\left( x \right) = \;p\left( x \right) + q\left( x \right) = \left( {{a_o} + {b_o}} \right) + \left( {{a_1} + {b_1}} \right)x + \left( {{a_2} + {b_2}} \right){x^2}\; \in {P_2}\]
\[\left( {\alpha p} \right)\left( x \right) = \alpha p\left( x \right) = \left( {\alpha {a_o}} \right) + \left( {\alpha {a_1}} \right)x + \left( {\alpha {a_2}} \right){x^2}\; \in {P_2}\]
Puede demostrarse que estas operaciones verifican todos los axiomas de espacio vectorial.
En particular, el vector nulo en este espacio es el polinomio nulo, es decir el polinomio cuyos coeficientes son todos iguales a cero.
Generalizando, para cualquier \(n \ge 0\) , el conjunto \({P_n}\) de todos los polinomios de grado menor o igual que \(n\) (incluyendo el polinomio nulo) es un espacio vectorial.
Observación:
¿Por qué no definimos \({P_n}\) como el conjunto de polinomios de grado exactamente igual a \(n\)? Si lo definiéramos así, no sería un espacio vectorial como se muestra en el siguiente ejemplo:
\(p\left( x \right) = {x^2}\;\) y \(q\left( x \right) = – {x^2} + 1\) son polinomios de grado 2, pero la suma es un polinomio de grado cero. Entonces no se verificaría el primer axioma de espacio vectorial (la suma de vectores de un espacio vectorial \(V\) debe estar en \(V\)).
Propiedades de los espacios vectoriales
A partir de los axiomas de espacios vectoriales, pueden demostrarse estas propiedades que resultan «naturales»:
Propiedad 1
\[0\;u = {0_V}\]
Propiedad 2
\[\alpha \;{0_V} = {0_V}\]
Propiedad 3
\[\left( { – \alpha } \right)u = – \left( {\alpha u} \right)\]
En particular, para \(\alpha = 1\) :\(\left( { – 1} \right)u = – u\)
Propiedad 4
\[\alpha \;u = {0_V}\; \Rightarrow \;\;\alpha = 0\; \vee \;\;u = {0_V}\]
Veamos cómo puede demostrarse esta última propiedad:
Si \(\alpha = 0\) , se cumple la proposición.
Si \(\alpha \ne 0\) , podemos multiplicar por \(\frac{1}{\alpha }\) :
\[\alpha \;u = {0_V}\; \Rightarrow \frac{1}{\alpha }\alpha \;u = \frac{1}{\alpha }\;{0_V} \Rightarrow u = {0_V}\;\]
¡Demostrado!
Subespacios vectoriales
Definición
Sea \(V\) un espacio vectorial y \(W\) un subconjunto no vacío de \(V\).
\(W\) es un subespacio de \(V\) si \(W\) es en sí mismo un espacio vectorial con las mismas operaciones (suma de vectores y producto por un escalar) definidas en \(V\).
Ejemplo
\(W = \left\{ {\;\left( {{x_1},{x_2}} \right)\; \in {R^2}\;:{x_2} = 3{x_1}\;} \right\}\) ¿es un subespacio de \({\mathbb{R}^2}\)?
Primero analicemos el conjunto \(W\). Son todos vectores de \({\mathbb{R}^2}\) tales que la segunda componente es el triple de la primera:
\[\left( {{x_1},3{x_1}} \right) = {x_1}\left( {1,3} \right)\]
\(W\) es la recta que pasa por el origen y tiene vector director (1,3), o sea la recta de ecuación y = 3x.
Para decidir si \(W\) es un subespacio de \({\mathbb{R}^2}\) habría que verificar que se cumplen los axiomas del 1 al 10. El lector puede comprobar que todos se cumplen en este caso.
Pero en general no es necesario verificar los axiomas porque existe un criterio sencillo para determinar si un subconjunto \(W\) de un espacio vectorial \(V\) es un subespacio, es el que sigue.
Condiciones necesarias y suficientes para caracterizar subespacios
\(W\) es subespacio de \(V\) si y sólo si se cumplen las siguientes condiciones:
a. \({0_V}\) está en \(W\).
b. Si \(u\) y \(v\) están en \(W\), entonces \(u + v\) está en \(W\).
c. Si \(u\) está en \(W\) y \(k\) es un escalar, \(ku\) está en \(W\).
Observaciones
1. La condición (a) asegura que W no es vacío. La mejor manera de comprobar si W es un subespacio es buscar primero si contiene al vector nulo. Si \({0_V}\) está en W, entonces deben verificarse las propiedades (b) y (c). Si \(\;{0_V}\) no está en W, W no puede ser un subespacio y no hace falta verificar las otras propiedades.
2. Las propiedades a, b y c corresponden a los axiomas 4, 1 y 6 de espacios vectoriales.
3. Los axiomas 2, 3, 7, 8, 9 y 10 de espacio vectorial se cumplen para \(W\) porque éste es un subconjunto de \(V\). Puede decirse que \(W\) «hereda» esas propiedades de \(V\).
4. Faltaría comprobar que cada vector de \(W\) tiene su opuesto en \(W\) (axioma 5 de espacios vectoriales):
Teniendo en cuenta la condición (c) de subespacios,
c. Si \(u\) está en \(W\) y \(k\) es un escalar, \(ku\) está en \(W\).
Si tomamos \(k = – 1\), resulta:
Para cada \(u \in W\;,\;\;\left( { – 1} \right)u = – u\; \in W\).
Y por lo tanto cada vector de \(W\) tiene su opuesto en \(W\).
De las observaciones anteriores se deduce que las condiciones (a), (b) y (c) son suficientes para demostrar que \(W\) es un espacio vectorial, y por lo tanto subespacio de \(V\).
Subespacios triviales
Si \(V\) es un espacio vectorial, entonces \(V\) es un subespacio de sí mismo.
\({0_V} + {0_V} = {0_V}\) y \(k{0_V} = {0_V}\;\;\;para\;cualquier\;k\;real\)
Los subespacios \(\left\{ {{0_V}} \right\}\) y \(V\) se denominan subespacios triviales de \(V\).
Ejercitación sobre subespacios
Ejemplo 1
Consideremos el conjunto \(W = \left\{ {\left( {x,y} \right) \in {\mathbb{R}^2}\;\;|\;\;\;xy = 0} \right\}\), ¿Es un subespacio de \({\mathbb{R}^2}\)?
Se cumple (a) pues \(\left( {0,0} \right) \in W\)
No se cumple (b) porque la suma de dos vectores de \(W\) puede no estar en \(W\), por ejemplo:
\[\left( {1,0} \right) + \left( {0,1} \right) = \left( {1,1} \right) \notin W\]
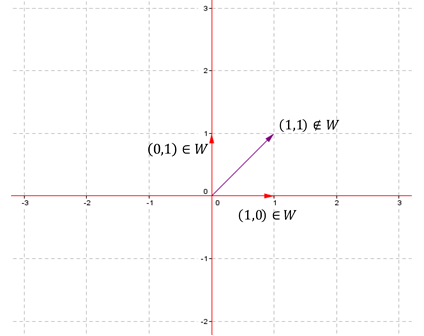
Entonces \(W\) no es un subespacio de \({\mathbb{R}^2}\).
Ejemplo 2
Consideremos el conjunto \(W = \left\{ {\left( {x,y} \right) \in {\mathbb{R}^2}\;\;|\;\;\;x = 0} \right\}\). Es decir, la recta de ecuación \(x = 0\). ¿Es un subespacio de \({\mathbb{R}^2}\)?
Se cumple (a) pues \(\left( {0,0} \right) \in W\)
Se cumple (b) pues la suma de dos vectores de \(W\), está en \(W\):
\[\left( {0,{y_1}} \right) + \left( {0,{y_2}} \right) = \left( {0,{y_1} + {y_2}} \right)\]
Se cumple (c) pues el producto de un vector de \(W\) por un número real está en \(W\):
\[k\left( {0,y} \right) = \left( {0,ky} \right)\]
Luego \(W\) es subespacio de \({\mathbb{R}^2}\).
Ejemplo 3
Consideremos el conjunto \(W = \left\{ {\left( {x,y} \right) \in {\mathbb{R}^2}\;\;|\;\;{x^2} – {y^2} = 0} \right\}\). ¿Es un subespacio de \({\mathbb{R}^2}\)?
\[{x^2} – {y^2} = 0 \Leftrightarrow y = x \vee x = – y\]
Se cumple (a) pues \(\left( {0,0} \right) \in W\)
No se cumple (b) porque la suma de dos vectores de \(W\) puede no estar en \(W\), por ejemplo:
\[\left( {1,1} \right) + \left( {1, – 1} \right) = \left( {2,0} \right) \notin W\]
Entonces \(W\) no es un subespacio de \({\mathbb{R}^2}\).
Ejemplo 4
Consideremos el conjunto \(W = \left\{ {\left( {x,y,z} \right) \in {\mathbb{R}^3}\;\;|\;\;x + y + 2z = 0} \right\}\). Es decir un plano que pasa por el origen. ¿Es un subespacio de \({\mathbb{R}^3}\)?
De la ecuación del plano se deduce que: \(x = – y – 2z\)
Por lo tanto los vectores que pertenecen a \(W\) responden a la forma \(\left( { – y – 2z,y,z} \right)\) con \(y,z \in \mathbb{R}\).
Se cumple (a) pues \(\left( {0,0,0} \right) \in W\)
Se cumple (b) pues la suma de dos vectores del plano, sigue estando en ese plano:
\[\left( { – y – 2z,\;y,z} \right) + \left( {-y’ – 2z’,y’,z’} \right) = \left( {\; – \left( {y + y’} \right) – 2\left( {z + z’} \right)\;,\;y + y’,z + z’\;} \right)\]
Se cumple \(\left( c \right)\) pues \(k\left( { – y – 2z,y,z} \right) = \left( { – ky – 2kz,ky,kz} \right) \in W\)
Entonces \(W\) es subespacio de \({\mathbb{R}^3}\).
Ejemplo 5
Consideremos el conjunto \(W = \left\{ {p \in {P_2}\;\;|\;p\left( 0 \right) = 0\;} \right\}\). Es decir, los polinomios de grado menor o igual que 2 (incluyendo el polinomio nulo) tales que evaluados en \(0\) dan por resultado \(0\). ¿Es un subespacio de \({P_2}\)?
Se cumple (a) pues el polinomio nulo pertenece a \(W\).
Recordemos la definición de suma de funciones y de producto de un real por una función:
\(\left( {f\; + \;g} \right)\;\left( x \right)\; = \;f\left( x \right)\; + \;g\left( x \right)\), para todo \(x\) perteneciente al dominio de \(f\) y de \(g\)
\(\left( {kf} \right)\left( x \right) = \;k\;f\left( x \right)\) para todo \(x\) perteneciente al dominio de \(f\).
Los polinomios son funciones, por lo tanto si consideramos \(p\;,\;q \in W\), resulta:
\[\left( {p + q} \right)\left( 0 \right) = p\left( 0 \right) + q\left( 0 \right) = 0 + 0 = 0\; \Rightarrow \;\;p + q \in W\]
\[\left( {kp} \right)\left( 0 \right) = k.p\left( 0 \right) = k\;0 = 0 \Rightarrow kp \in W\;\]
Demostramos que \(W\) es un subespacio de \({P_2}\).
Ejemplo 6
Consideremos el conjunto \(W = \left\{ {A \in {\mathbb{R}^{2 \times 2}}\;\;|\;A = {A^t}\;} \right\}\). Es decir, el conjunto de matrices simétricas de \(2 \times 2\).
Se cumple (a) porque la matriz nula pertenece a \(W\).
Se cumple (b) pues si \(A,B \in W\) entonces \({\left( {A + B} \right)^t} = {A^t} + {B^t} = A + B\), luego \(\left( {A + B} \right) \in W\)
Se cumple (c) pues si \(A \in W\) entonces \({\left( {kA} \right)^t} = k{A^t} = kA\), luego \(\left( {kA} \right) \in W\)
Demostramos que el conjunto de matrices simétricas de \(2\times 2\) es un subespacio de \(\mathbb{R}^{2 \times 2}\).
Observación: En la comprobación de las condiciones (a), (b) y (c) no fue necesario hacer referencia al tamaño de las matrices. Esto significa que es válido para matrices simétricas de \(n \times n\).
Ejemplo 7
Consideremos el conjunto \(W = \left\{ {A \in {\mathbb{R}^{2 \times 2}}\;\;|\det \left( A \right) = 0\;} \right\}\). ¿Es un subespacio de \({\mathbb{R}^{2 \times 2}}\)?
Se cumple (a) porque la matriz nula pertenece a \(W\).
En general \(\det \left( {A + B} \right) \ne \det \left( A \right) + \det \left( B \right)\), entonces podría ocurrir que \(A,B \in W\) pero que \(A + B\) no esté en \(W\). Por ejemplo
\[A = \left( {\begin{array}{*{20}{c}}1&{ – 3}\\{ – 1}&3\end{array}} \right)\;\;,\;\;\;B = \left( {\begin{array}{*{20}{c}}0&0\\{ – 2}&5\end{array}} \right)\;\;,\;\;\;A + B = \left( {\begin{array}{*{20}{c}}1&{ – 3}\\{ – 3}&8\end{array}} \right)\]
Entonces no se cumple (b).
\(W\) no es un subespacio de \({\mathbb{R}^{2 \times 2}}\).
Resumen de los subespacios de \({\mathbb{R}^2}\) y \({\mathbb{R}^3}\)
Después de estos ejemplos podemos resumir cuales son los diferentes tipos de subespacios de \({\mathbb{R}^2}\) y \({\mathbb{R}^3}\):
No hay ninguna otra clase de subespacios en \({\mathbb{R}^2}\) y \({\mathbb{R}^3}\).
Videos relacionados
