El siguiente es el enunciado y resolución completa del segundo parcial de álgebra y geometría analítica tomado el día 04-11-2017, en el curso semi-presencial.
Enunciado del segundo parcial de álgebra [04-11-2017]

Ejercicio 1 – Transformaciones lineales
Sea \(T:{\mathbb{R}^3} \to {P_2}\) transformación lineal | \(A = M{\left( T \right)_{EB}} = \left( {\begin{array}{*{20}{c}}1&0&h\\0&0&0\\h&0&4\end{array}} \right)\), con \(E\) base canónica de \({\mathbb{R}^3}\) y \(B = \left\{ {1,1 + x,{x^2}} \right\}\) base de \({P_2}\).
a) Hallar los valores de \(h\) para que \(\dim \left( {Nu\left( T \right)} \right) = 2\).
b) Si \(h = 2\), determinar si \(p\left( x \right) = – 3 – 6{x^2} \in Im\left( T \right)\)
Resolución del ejercicio 1
Ítem a
Recordemos que la dimensión del núcleo, de la imagen y del dominio de la transformación se relacionan con el teorema de las dimensiones:
\[\dim \left( {{\mathbb{R}^3}} \right) = \dim \left( {Nu} \right) + \dim \left( {Im} \right)\]
\[3 = \dim \left( {Nu} \right) + \dim \left( {Im} \right)\]
Entonces que la dimensión del núcleo sea igual a 2, es equivalente a que la dimensión de la imagen sea igual a 1.
Pero la dimensión de la imagen es igual al rango de la matriz asociada:
\[\dim \left( {Im} \right) = rg\left( {M{{\left( T \right)}_{EB}}} \right)\]
Calculemos entonces el rango de la matriz. (Para recordar cómo buscar el rango leé acá).
Para escalonar la matriz primero intercambiamos fila 2 y fila 3:
\[\left( {\begin{array}{*{20}{c}}1&0&h\\0&0&0\\h&0&4\end{array}} \right)\mathop \to \limits_{{F_3} \leftrightarrow {F_2}} \left( {\begin{array}{*{20}{c}}1&0&h\\h&0&4\\0&0&0\end{array}} \right)\]
Ahora suponiendo que \(h \ne 0\) restamos a la fila 2 por \(h\) veces la fila 1 (así generamos un cero en \({a_{21}}\)):
\[\mathop \to \limits_{{F_2} – h.{F_1}} \left( {\begin{array}{*{20}{c}}1&0&h\\0&0&{4 – {h^2}}\\0&0&0\end{array}} \right)\]
(En el caso de que \(h = 0\), la matriz es \(\left( {\begin{array}{*{20}{c}}1&0&0\\0&0&0\\0&0&4\end{array}} \right)\), y tiene rango 2)
Entonces:
- Si \(4 – {h^2} = 0\) el rango de la matriz es 1.
- Si \(4 – {h^2} \ne 0\) el rango de la matriz es 2.
Para que \(4 – {h^2} = 0\) debe ser \(h = 2\) o \(h = – 2\).
Finalmente para que \(\dim \left( {Nu} \right) = 2\) debe ser \(h = 2\) o \(h = – 2\).
Ítem b
Si \(h = 2\) la matriz es:
\[M{\left( T \right)_{EB}} = \left( {\begin{array}{*{20}{c}}1&0&2\\0&0&0\\2&0&4\end{array}} \right)\]
Hay muchas formas correctas (y diferentes) de resolver este ítem.
Nosotros, para determinar si \(p\left( x \right) = – 3 – 6{x^2} \in Im\left( T \right)\), vamos a optar por hallar la imagen de la transformación lineal.
Podemos obtener la imagen transformando a los vectores de una base del dominio:
\[B = \left\{ {\color{red}{1},\color{green}{1 + x},\color{blue}{{x^2}}} \right\}\]
\[{\left[ {T\left( {1,0,0} \right)} \right]_B} = \left( {\begin{array}{*{20}{c}}1&0&2\\0&0&0\\2&0&4\end{array}} \right)\left( {\begin{array}{*{20}{c}}1\\{\begin{array}{*{20}{c}}0\\0\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}1\\{\begin{array}{*{20}{c}}0\\2\end{array}}\end{array}} \right)\]
\[ \Rightarrow T\left( {1,0,0} \right) = 1.\left( \color{red}{1} \right) + 0.\left( {\color{green}{1 + x}} \right) + 2.\left( {\color{blue}{{x^2}}} \right) = 1 + 2{x^2}\]
\[{\left[ {T\left( {0,1,0} \right)} \right]_B} = \left( {\begin{array}{*{20}{c}}1&0&2\\0&0&0\\2&0&4\end{array}} \right)\left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}1\\0\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}0\\0\end{array}}\end{array}} \right)\]
\[ \Rightarrow T\left( {1,0,0} \right) = 0.\left( \color{red}{1} \right) + 0.\left( {\color{green}{1 + x}} \right) + 0.\left( {\color{blue}{{x^2}}} \right) = 0{x^2} + 0x + 0\]
\[{\left[ {T\left( {0,0,1} \right)} \right]_B} = \left( {\begin{array}{*{20}{c}}1&0&2\\0&0&0\\2&0&4\end{array}} \right)\left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}0\\1\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}2\\{\begin{array}{*{20}{c}}0\\4\end{array}}\end{array}} \right)\]
\[ \Rightarrow T\left( {1,0,0} \right) = 2.\left( \color{red}{1} \right) + 0.\left( {\color{green}{1 + x}} \right) + 4.\left( {\color{blue}{{x^2}}} \right) = 2 + 4{x^2}\]
Cómo los transformados de una base del dominio generan la imagen:
\[Im\left( T \right) = gen\left\{ {1 + 2{x^2},2 + 4{x^2}} \right\}\]
Pero \(2 + 4{x^2} = 2\left( {1 + 2{x^2}} \right)\), entonces:
\[{B_{Im}} = \left\{ {1 + 2{x^2}} \right\}\]
Ahora que tenemos una base de la imagen podemos decidir si \( – 3 – 6{x^2} \in Im\left( T \right)\).
Sí pertenece pues:
\[ – 3 – 6{x^2} = \left( {1 + 2{x^2}} \right).\left( { – 3} \right)\]
Ejercicio 2 – Diagonalización
Si \(M = \left( {\begin{array}{*{20}{c}}3&1&2\\0&a&0\\1&{ – 1}&2\end{array}} \right)\), hallar los valores de \(a\) para los cuales la matriz \(M\) es diagonalizable.
Resolución
Busquemos los autovalores de M resolviendo la ecuación \(\det \left( {M – \lambda .I} \right) = 0\):
\[\left| {\begin{array}{*{20}{c}}{3 – \lambda }&1&2\\0&{a – \lambda }&0\\1&{ – 1}&{2 – \lambda }\end{array}} \right| = 0\]
Conviene calcular el determinante por la fila 2, porque tenemos dos ceros:
\[ \Rightarrow \left( {a – \lambda } \right)\left[ {\left( {3 – \lambda } \right)\left( {2 – \lambda } \right) – 2} \right] = 0\]
\[ \Rightarrow \left( {a – \lambda } \right)\left[ {6 – 5\lambda + {\lambda ^2} – 2} \right] = 0\]
\[ \Rightarrow \left( {a – \lambda } \right)\left[ {4 – 5\lambda + {\lambda ^2}} \right] = 0\]
\[ \Rightarrow \left( {a – \lambda } \right)\left( {\lambda – 4} \right)\left( {\lambda – 1} \right) = 0\]
Entonces los autovalores de \(M\) son:
\[\lambda = a \vee \lambda = 4 \vee \lambda = 1\]
Sabemos que para que \(M\) sea diagonalizable debe tener exactamente tres autovectores LI.
Y también sabemos que autovalores diferentes están asociados a autovectores LI.
Así que: si \(a \ne 4 \wedge a \ne 1\), \(M\) es diagonalizable.
Pero: ¿qué pasa si \(a = 1\) o si \(a = 4\)? Tenemos que analizarlo. Si ocurriera que el autovalor doble tiene asociado un autoespacio de dimensión 2, también sería diagonalizable en ese caso. Pero lo tenemos que analizar.
Caso \(a = 1\).
Autoespacio asociado a \(\lambda = 1\) (autovalor doble)
\[\left( {\begin{array}{*{20}{c}}2&1&2\\0&0&0\\1&{ – 1}&1\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\{\begin{array}{*{20}{c}}y\\z\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}0\\0\end{array}}\end{array}} \right) \Rightarrow \left\{ {\begin{array}{*{20}{c}}{2x + y + 2z = 0}\\{x – y + z = 0}\end{array}} \right.\]
\[ \Rightarrow \dim \left( {{S_{\lambda = 1}}} \right) = 1\]
No coincide la multiplicidad algebraica de \(\lambda = 1\;\)(doble) con la multiplicidad geométrica.
Entonces la matriz \(M\) no es diagonalizable en este caso.
Caso \(a = 4\).
Autoespacio asociado a \(\lambda = 4\) (autovalor doble)
\[\left( {\begin{array}{*{20}{c}}{ – 1}&1&2\\0&0&0\\1&{ – 1}&{ – 2}\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\{\begin{array}{*{20}{c}}y\\z\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}0\\0\end{array}}\end{array}} \right) \Rightarrow \left\{ {\begin{array}{*{20}{c}}{ – x + y + 2z = 0}\\{x – y – 2z = 0}\end{array}} \right.\]
\[ \Rightarrow \dim \left( {{S_{\lambda = 4}}} \right) = 2\]
Coincide la multiplicidad algebraica de \(\lambda = 4\;\)(doble) con la multiplicidad geométrica.
Entonces la matriz \(M\) es diagonalizable en este caso.
Podemos concluir que:
\[M\;es\;diagonalizable\;si\;a \in \mathbb{R} – \left\{ 1 \right\}\]
Ejercicio 3 – Cónicas
a) Obtener la ecuación cartesiana y graficar (en el intervalo indicado) la curva dada por:
\(\left\{ {\begin{array}{*{20}{c}}{x = – 2{{\left( {t – 1} \right)}^2}}\\{y = 1 + t}\end{array}\;\;\;\;\;t \in \left[ { – 1,1} \right]} \right.\)
Indicar el sentido de recorrido sobre la curva.
b) Parametrizar la curva \({x^2} + 4{\left( {y – 1} \right)^2} = 4\) con \(y \le 1\). Graficar indicando el sentido de recorrido.
Resolución del ejercicio 3
Ítem a
La ecuación paramétrica es:
\[\left\{ {\begin{array}{*{20}{c}}{x = – 2{{\left( {t – 1} \right)}^2}}\\{y = 1 + t}\end{array}\;\;\;\;\;t \in \left[ { – 1,1} \right]} \right.\]
Para obtener la ecuación cartesiana, despejemos \(t\) en función de \(y\) reemplacemos en la primera expresión:
\[t = y – 1\]
\[ \Rightarrow x = – 2{\left( {y – 1 – 1} \right)^2}\]
\[ \bbox[yellow,5px]
{
\Rightarrow x = – 2{\left( {y – 2} \right)^2}
}
\]
Esta es la ecuación cartesiana de una parábola con vértice en \(\left( {0,2} \right)\), y eje focal de ecuación \(y = 2\). Las “ramas” de la parábola apuntan hacia la izquierda porque el coeficiente es negativo.
La gráfica de \(x = – 2{\left( {y – 2} \right)^2}\) es:
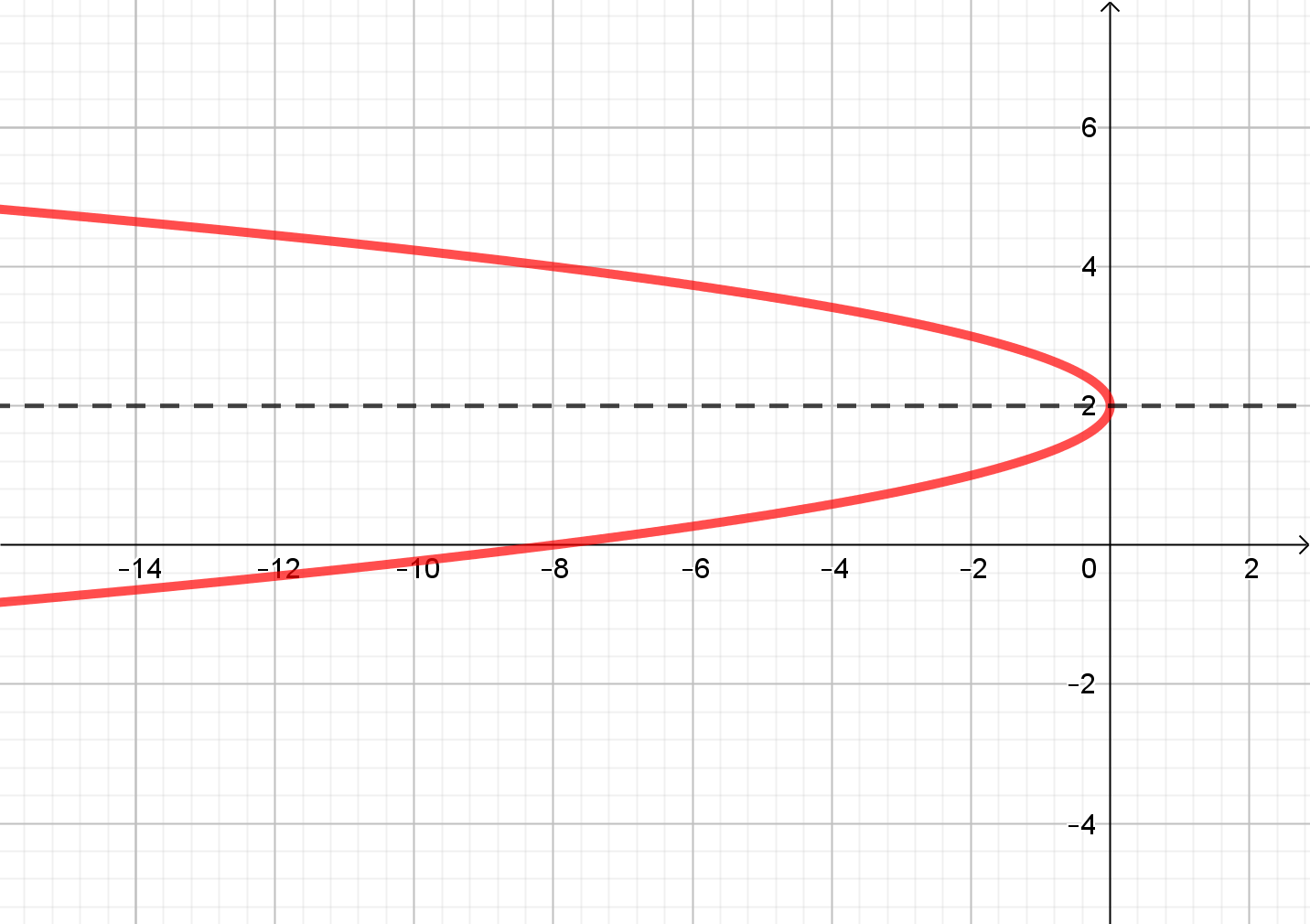
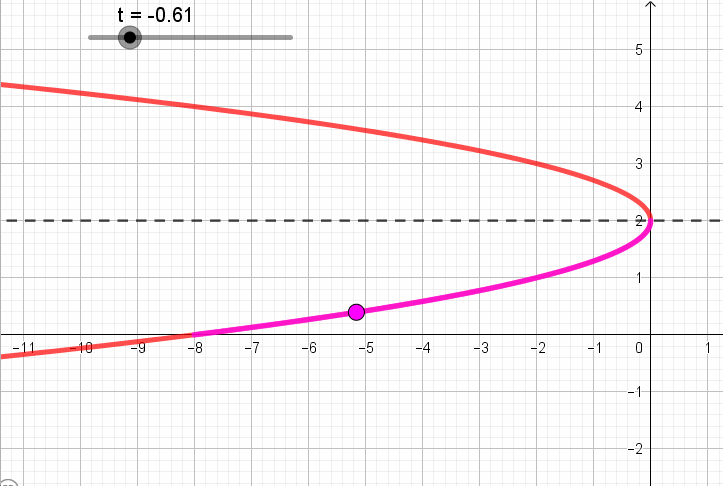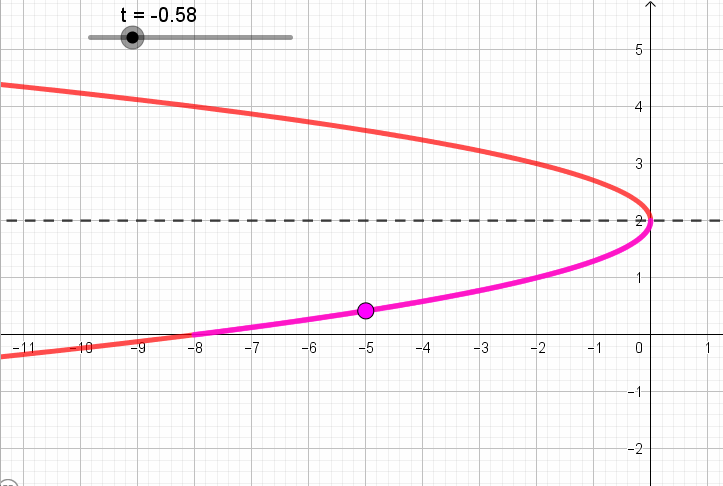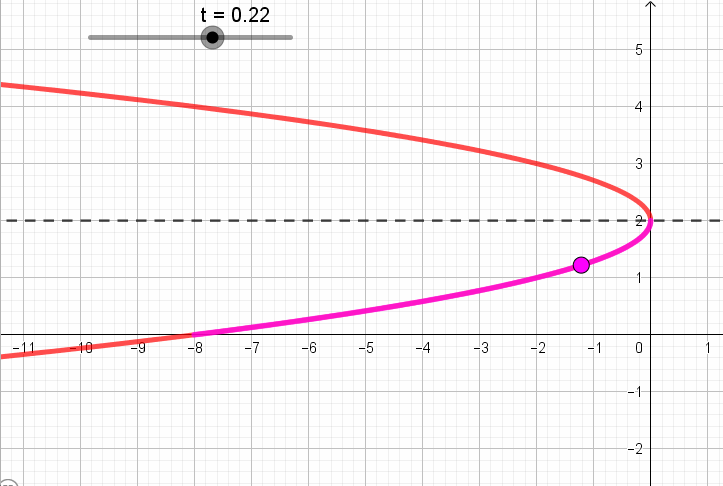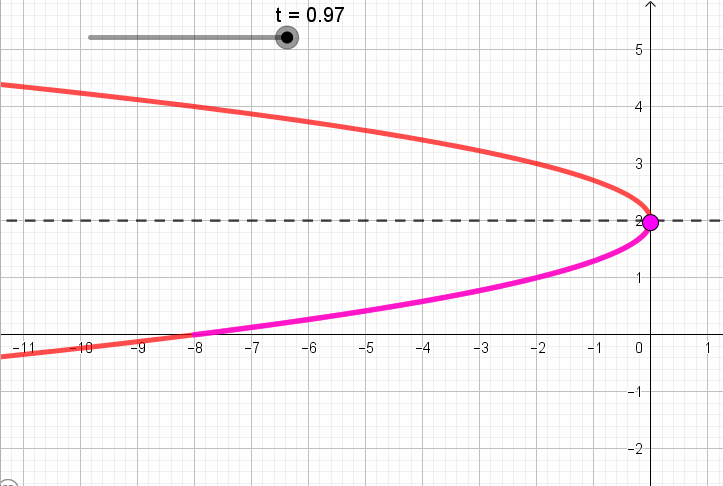
Pero, en la parametrización se establece que \(t \in \left[ { – 1,1} \right]\). Así que la curva definida no es “toda” la parábola, sino sólo un arco.
Para reconocer que parte de la parábola está definida por la expresión y también el sentido de recorrido, tomemos algunos valores de \(t \in \left[ { – 1,1} \right]\) y veamos que puntos se obtienen para esos valores:
Si \(\;\color{red}{t = -1}\), obtenemos
\[\left\{ {\begin{array}{*{20}{c}}{x = – 2{{\left( { \color{red}{-1} – 1} \right)}^2} = – 8}\\{y = 1 – 1 = 0}\end{array}} \right.\]
Si\(\;\color{red}{t=0}\), obtenemos
\[\left\{ {\begin{array}{*{20}{c}}{x = – 2{{\left( {\color{red}{0} – 1} \right)}^2} = – 2}\\{y = 1 + \color{red}{0} = 1}\end{array}} \right.\]
Si\(\;\color{red}{t=1}\), obtenemos
\[\left\{ {\begin{array}{*{20}{c}}{x = – 2{{\left( { \color{red}{1} – 1} \right)}^2} = 0}\\{y = 1 + \color{red}{1} = 2}\end{array}} \right.\]
Resumiendo, obtuvimos que:
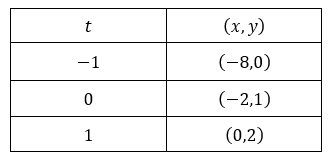
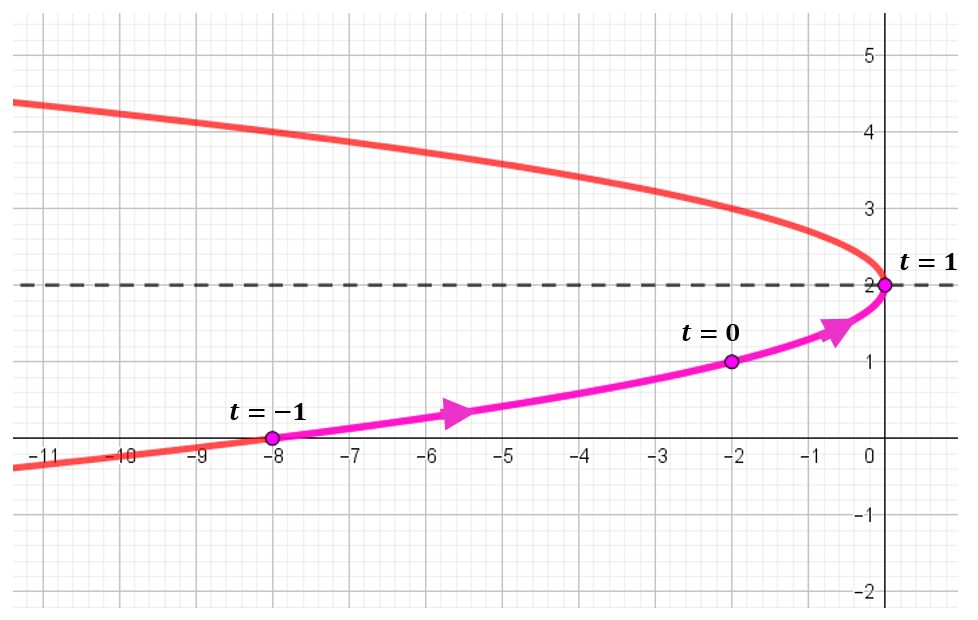
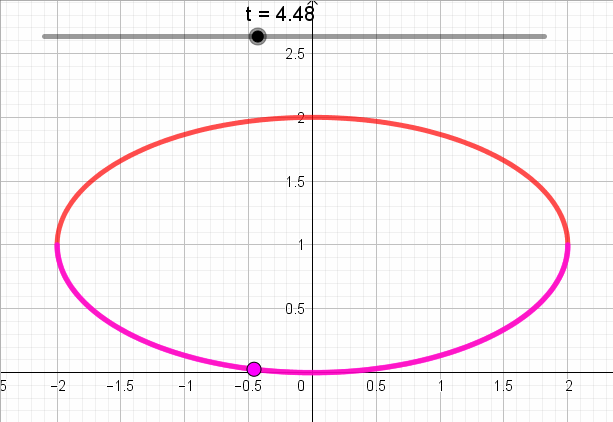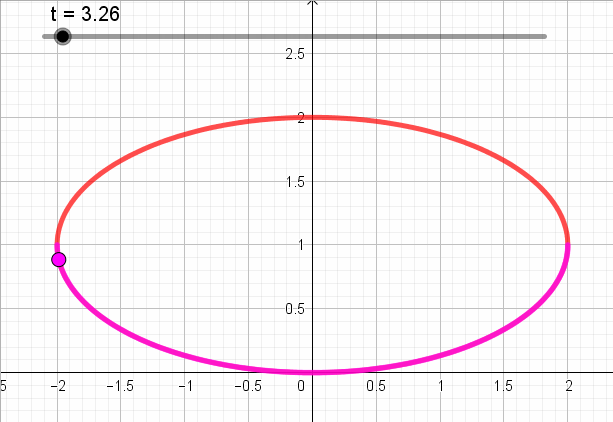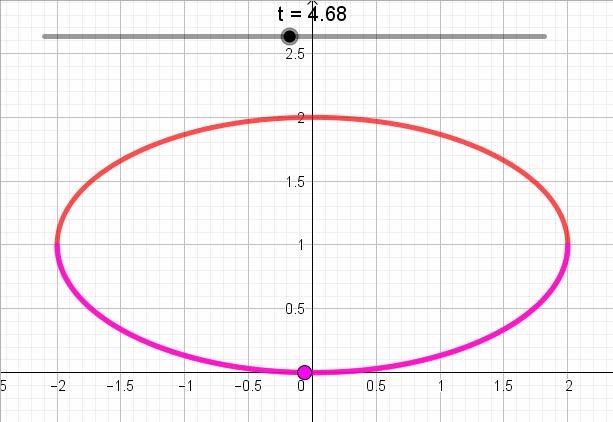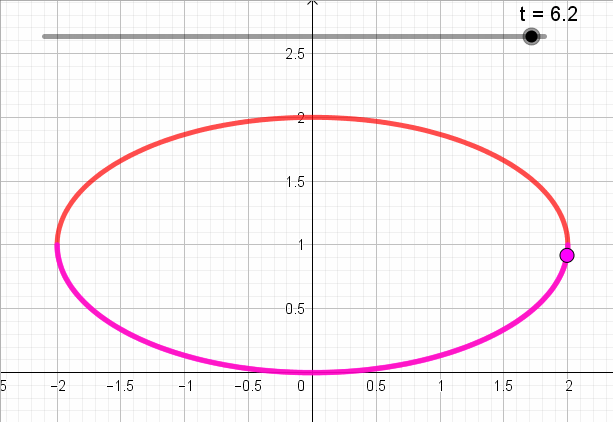
A continuación se ve una animación que muestra para cada valor de t, el punto que corresponde según la parametrización:
Ítem b
Parametrizar la curva \({x^2} + 4{\left( {y – 1} \right)^2} = 4\) con \(y \le 1\). Graficar indicando el sentido de recorrido.
\[{x^2} + 4{\left( {y – 1} \right)^2} = 4\]
Si dividimos a ambos miembros por 4:
\[\frac{{{x^2}}}{4} + {\left( {y – 1} \right)^2} = 1\]
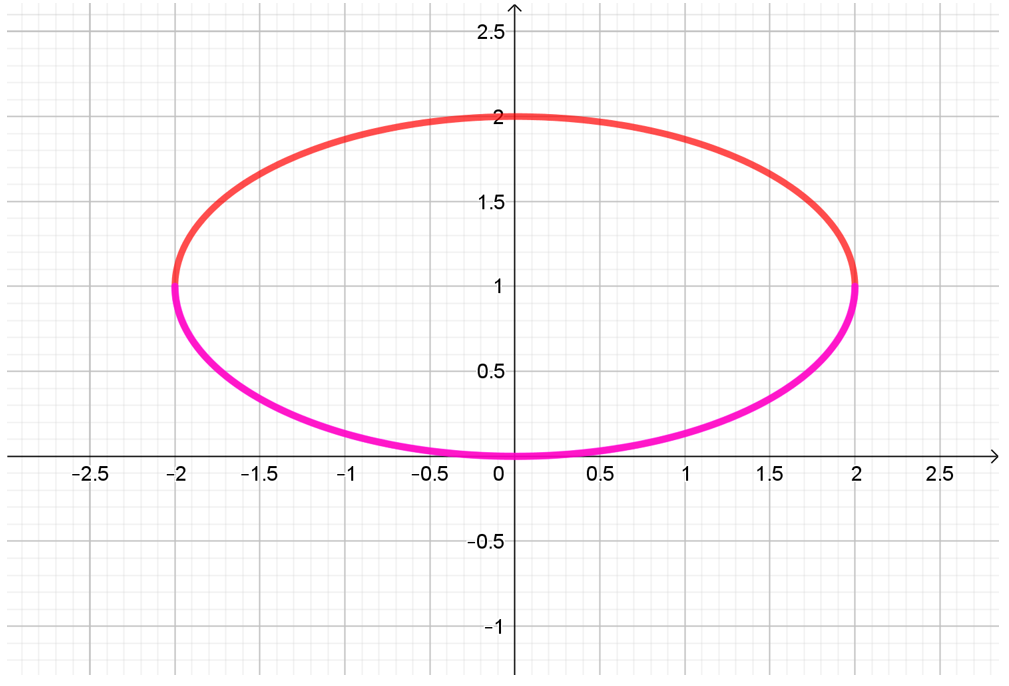
Se trata de la ecuación de una elipse centrada en \(\left( {0,1} \right)\) con semiejes 2 y 1, y eje focal de ecuación \(y = 1\).
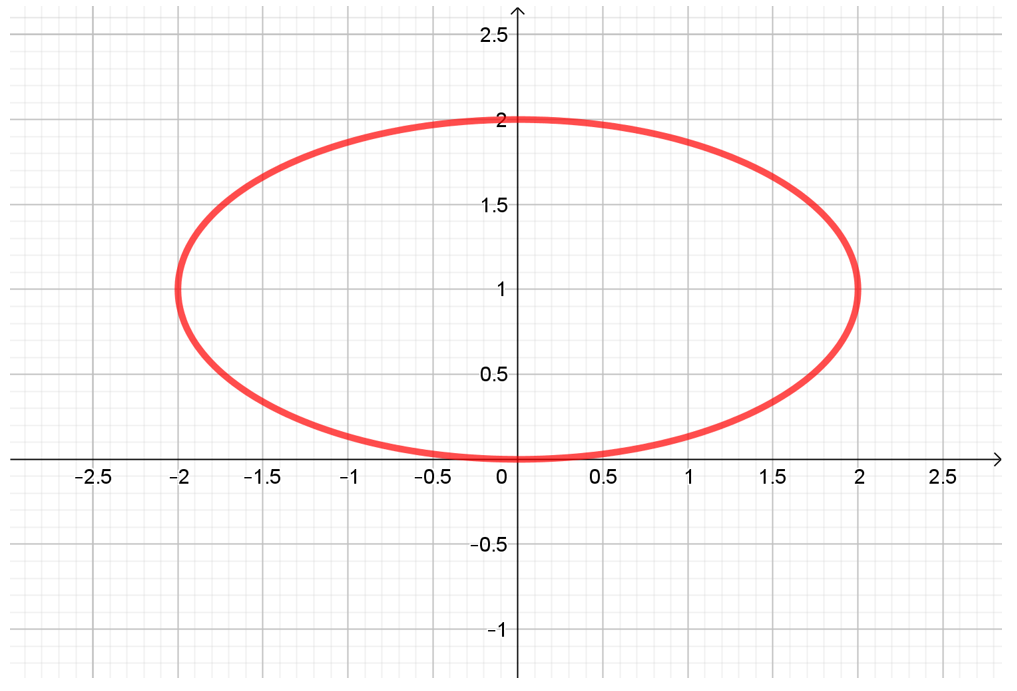
Pero si debe cumplirse que \(y \le 1\):
Para parametrizar a una elipse usamos la identidad pitagórica \({\cos ^2}\left( \alpha \right) + {\rm{se}}{{\rm{n}}^2}\left( \alpha \right) = 1\).
Podemos expresar la ecuación de la elipse cómo suma de dos cuadrados fácilmente:
\[{\left( {\frac{x}{2}} \right)^2} + {\left( {y – 1} \right)^2} = 1\]
Ahora sustituimos:
\[\left\{ {\begin{array}{*{20}{c}}{\frac{x}{2} = \cos \left( t \right)}\\{y – 1 = {\rm{sen}}\left( t \right)}\end{array}} \right.\]
Y podemos despejar \(x\) e \(y\):
\[\left\{ {\begin{array}{*{20}{c}}{x = 2.\cos \left( t \right)}\\{y = {\rm{sen}}\left( t \right) + 1}\end{array}} \right.\]
Para definir toda la elipse \(t \in \left[ {0,2\pi } \right]\).
Pero el enunciado pide que \(y \le 1\):
\[{\rm{sen}}\left( t \right) + 1 \le 1\]
\[ \Rightarrow {\rm{sen}} \left( t \right) \le 0\]
Sabemos (o deberíamos recordar) que el seno es negativo en los cuadrantes 3 y 4. Entonces: \(t \in \left[ {\pi ,2\pi } \right]\):
\[\left\{ {\begin{array}{*{20}{c}}{x = 2.\cos \left( t \right)}\\{y = {\rm{sen}}\left( t \right) + 1}\end{array}} \right.\;\;\;\;\;t \in \left[ {\pi ,2\pi } \right]\]
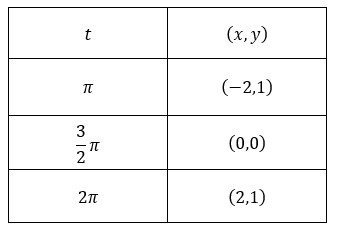
Para reconocer el sentido de recorrido, tomemos algunos valores de \(t \in \left[ {\pi ,2\pi } \right]\) y veamos que puntos se obtienen para esos valores:
Si \(\color{red}{t = \pi} \), obtenemos
\[\left\{ {\begin{array}{*{20}{c}}{x = 2.\cos \left( \color{red}{\pi} \right) = – 2}\\{y = {\rm{sen}}\left( \color{red}{\pi} \right) + 1 = 1}\end{array}} \right.\]
Si \(\color{red}{t = \frac{3}{2}\pi} \), obtenemos
\[\left\{ {\begin{array}{*{20}{c}}{x = 2.\cos \left( {\color{red}{\frac{3}{2}\pi} } \right) = 0}\\{y = {\rm{sen}}\left( {\color{red}{\frac{3}{2}\pi} } \right) + 1 = 0}\end{array}} \right.\]
Si \(\color{red}{t = 2\pi} \), obtenemos
\[\left\{ {\begin{array}{*{20}{c}}{x = 2.\cos \left( {\color{red}{2\pi} } \right) = 2}\\{y = {\rm{sen}}\left( {\color{red}{2\pi}} \right) + 1 = 1}\end{array}} \right.\]
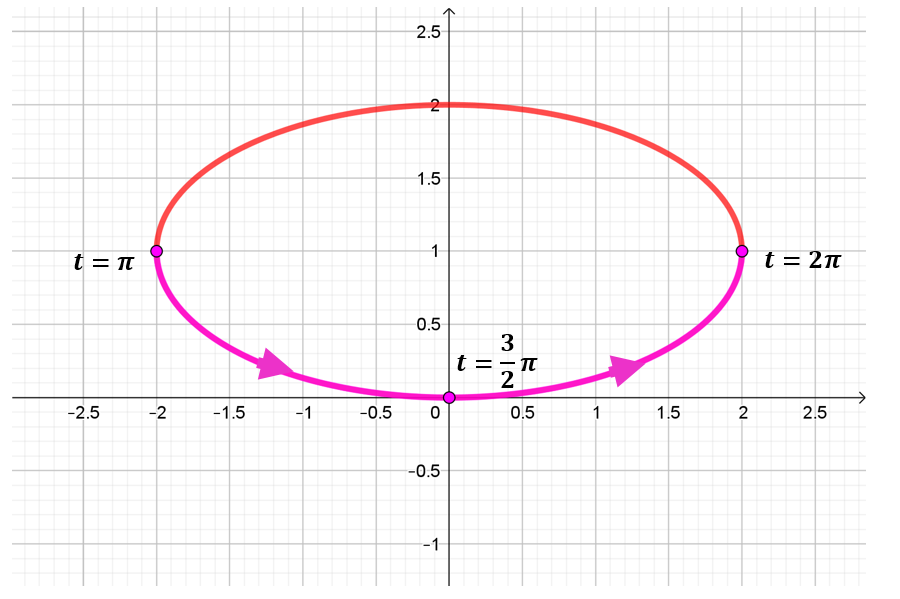
Resumiendo, obtuvimos que:
Entonces el sentido de recorrido es antihorario:
En la siguiente animación se puede ver para cada valor de t, el punto correspondiente del plano según la parametrización:
Ejercicio 4 – Superficies cuádricas
Sea la ecuación \({x^2} – {y^2} + 4{z^2} + 2y = A\)
a) Hallar los valores de \(A\) para los cuales corresponda a una superficie cónica.
b) Para \(A = 0\) identificar y graficar la superficie. Hallar la curva intersección de la superficie y el plano \(y = 4\), identifíquela e indique en el gráfico dicha curva.
Resolución del ejercicio 4
Ítem a
Recordemos que la ecuación de una superficie cónica es:
\(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} \color{red}{-} \frac{{{z^2}}}{{{c^2}}} = 0\;\) [Con eje sobre el eje z]
\(\frac{{{x^2}}}{{{a^2}}} \color{blue}{-} \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{c^2}}} = 0\;\) [Con eje sobre el eje y]
\( \color{green}{-} \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{c^2}}} = 0\;\) [Con eje sobre el eje x]
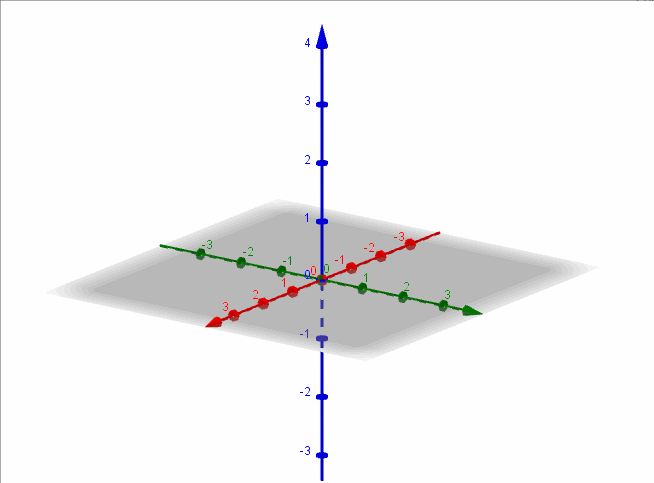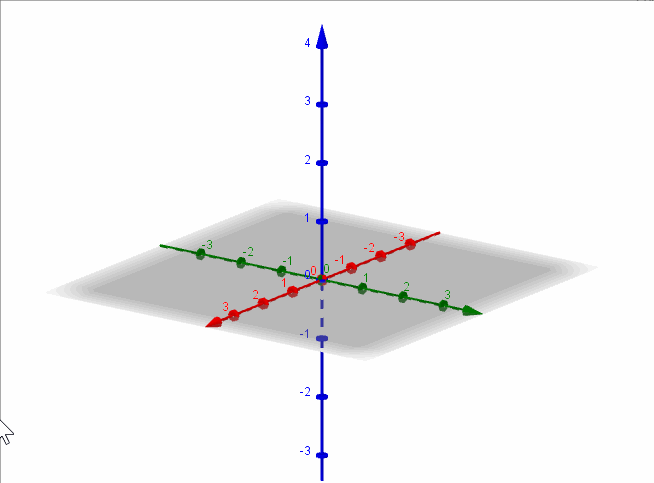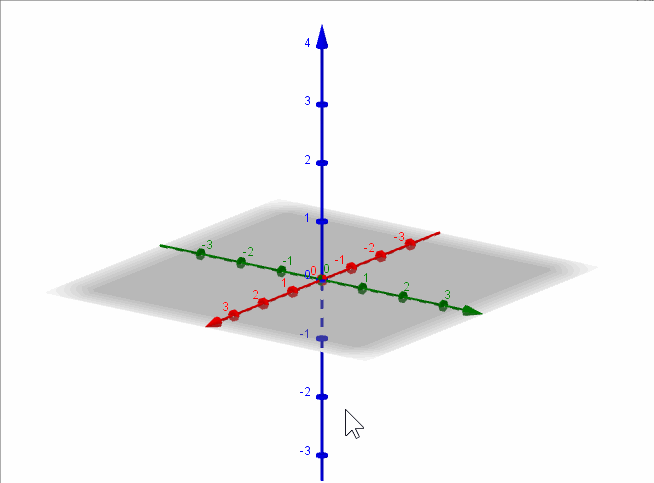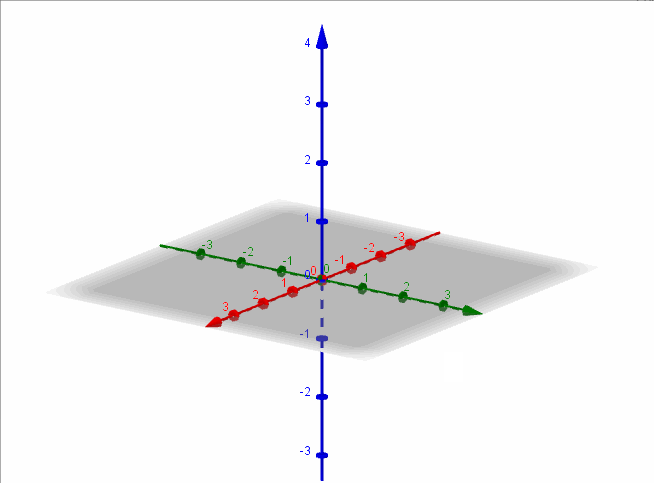
Entonces completamos cuadrados en \(y\):
\[{x^2} – {y^2} + 4{z^2} + 2y = A\]
\[ \Rightarrow {x^2} – \left( {{y^2} – 2y} \right) + 4{z^2} = A\]
Sumamos y restamos la mitad del coeficiente lineal de \(y\):
\[ \Rightarrow {x^2} – \left( {{y^2} – 2y + 1 – 1} \right) + 4{z^2} = A\]
Quedó \({y^2} – 2y + 1\) que es un trinomio cuadrado perfecto. Lo sustituimos por \({\left( {y – 1} \right)^2}\):
\[ \Rightarrow {x^2} – \left( {{{\left( {y – 1} \right)}^2} – 1} \right) + 4{z^2} = A\]
\[ \Rightarrow {x^2} – {\left( {y – 1} \right)^2} + 1 + 4{z^2} = A\]
\[ \Rightarrow {x^2} – {\left( {y – 1} \right)^2} + 4{z^2} = A – 1\]
Entonces para que sea una superficie cónica debe ser:
\[A = 1\]
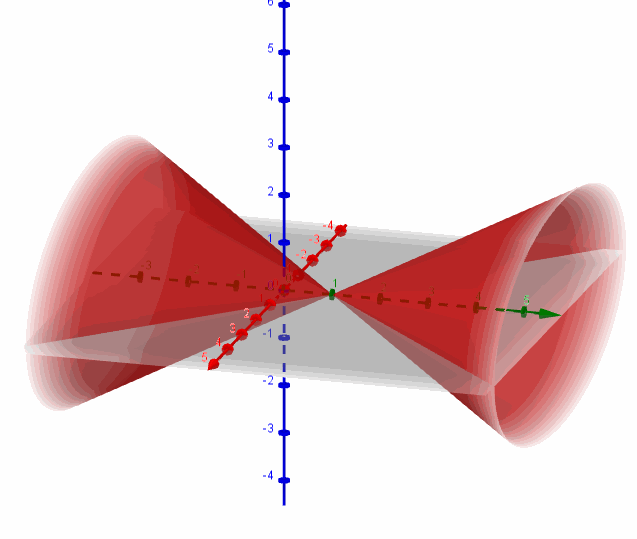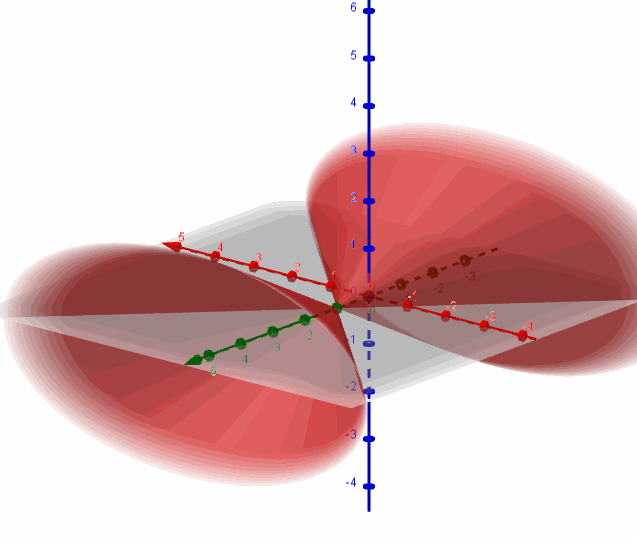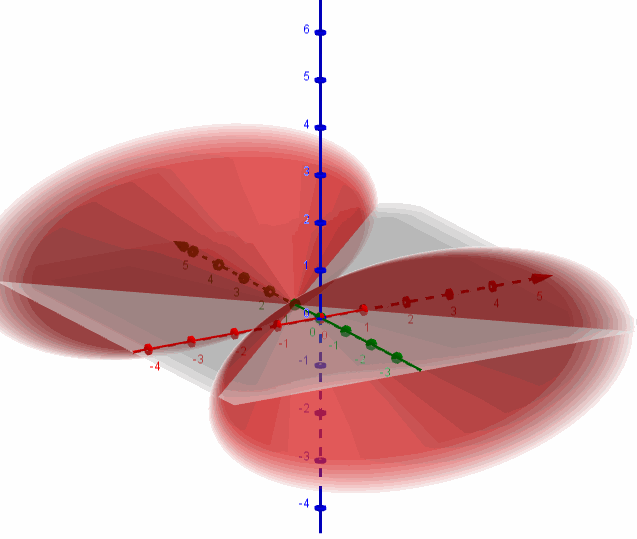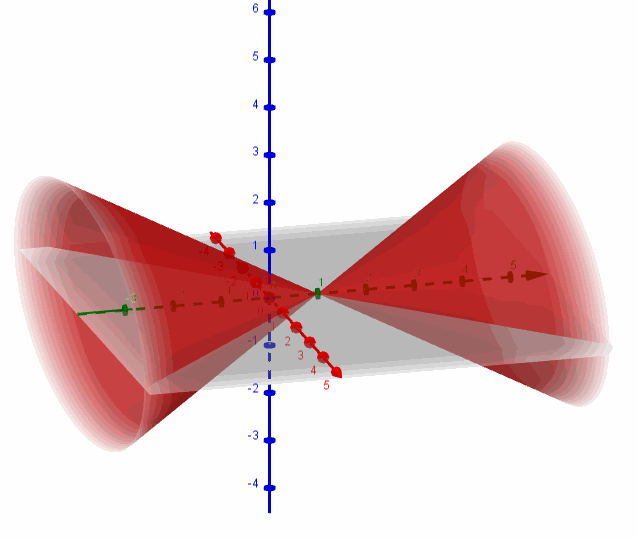
Ítem b
Usemos la expresión ya obtenida en el ítem a:
\[{x^2} – {\left( {y – 1} \right)^2} + 4{z^2} = A – 1\]
Para \(A = 0\):
\[{x^2} – {\left( {y – 1} \right)^2} + 4{z^2} = – 1\]
Multiplicamos por \( – 1\) a cada miembro:
\[ – {x^2} + {\left( {y – 1} \right)^2} – 4{z^2} = 1\]
Se trata de un hiperboloide de dos hojas con centro en \(\left( {0,1,0} \right)\) y eje igual al eje \(y\):
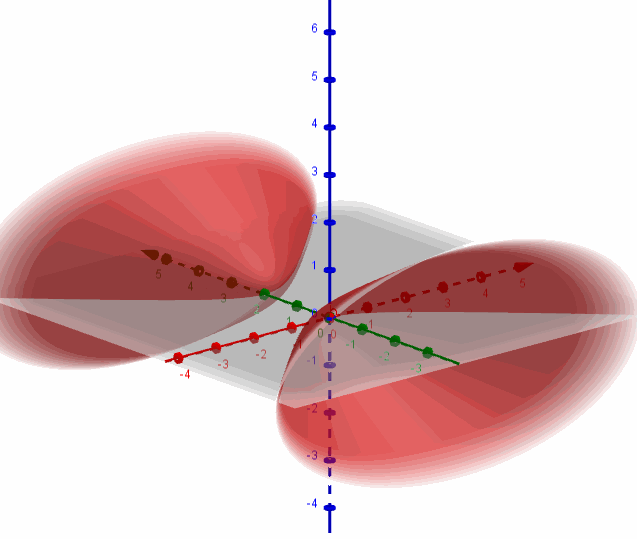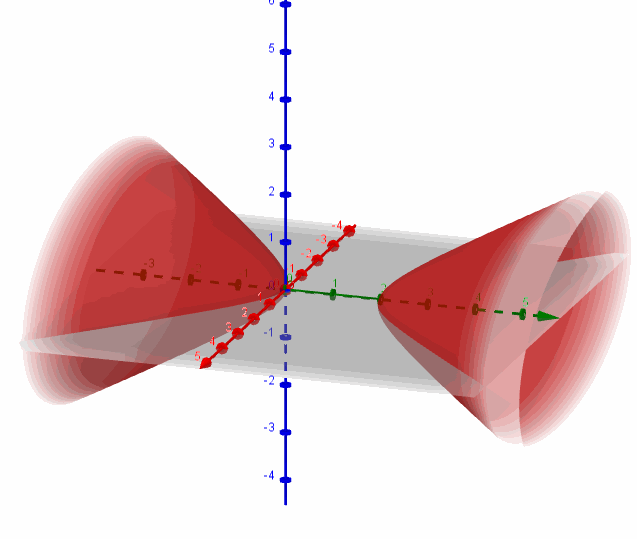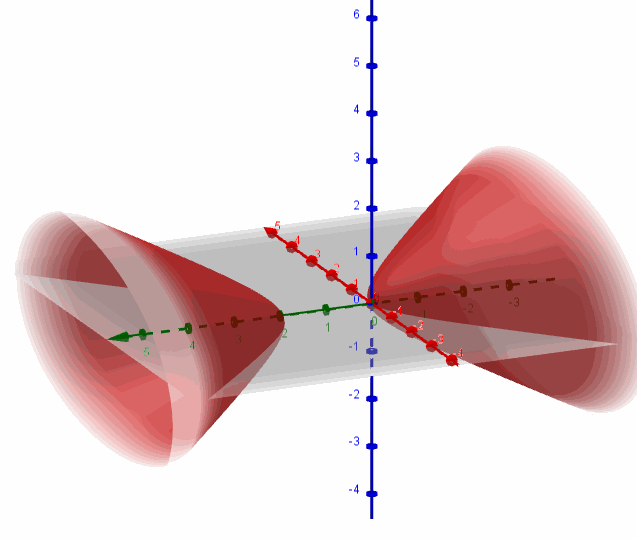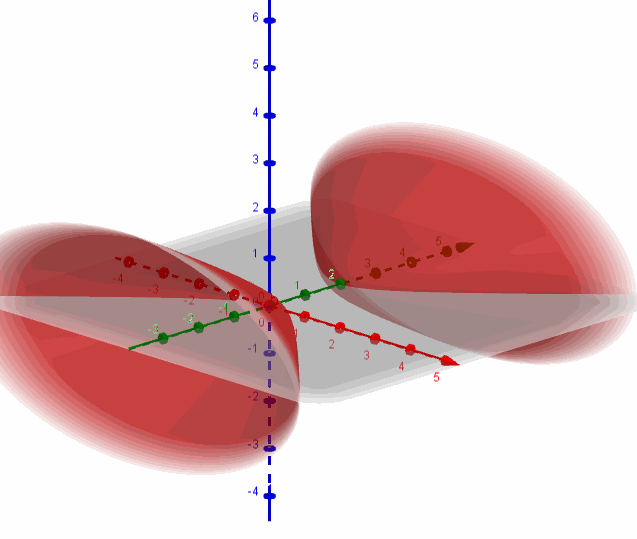
Hallemos la intersección de la superficie con el plano \(y = 4\):
\[\left\{ {\begin{array}{*{20}{c}}{ – {x^2} + {{\left( {4 – 1} \right)}^2} – 4{z^2} = 1}\\{y = 4}\end{array}} \right.\;\]
\[ \Rightarrow \;\;\left\{ {\begin{array}{*{20}{c}}{ – {x^2} – 4{z^2} = – 8}\\{y = 4}\end{array}} \right.\]
\[ \Rightarrow \;\;\left\{ {\begin{array}{*{20}{c}}{ – {x^2} – 4{z^2} = – 8}\\{y = 4}\end{array}} \right.\]
\[ \Rightarrow \;\;\left\{ {\begin{array}{*{20}{c}}{\frac{{{x^2}}}{8} + \frac{{{z^2}}}{2} = 1}\\{y = 4}\end{array}} \right.\]
Se trata de una elipse centrada en \(\left( {0,4,0} \right)\):

Ejercicio 5 – Números complejos
Determinar el conjunto de puntos del plano complejo que satisfacen:
\(\left| {z – \left( {4 + 3i} \right)} \right| \le 3\) y \(Re\left( z \right) \le 4\) \(z \in \mathbb{C}\)
Representar gráficamente.
Resolución del ejercicio 5
Representemos a \(z = x + i.y\).
Entonces reemplacemos:
\[\left| {x + y.i – 4 – 3i} \right| \le 3\]
\[ \Rightarrow \left| {\left( {x – 4} \right) + \left( {y – 3} \right).i} \right| \le 3\]
Calculamos el módulo del complejo:
\[ \Rightarrow \sqrt {{{\left( {x – 4} \right)}^2} + {{\left( {y – 3} \right)}^2}} \le 3\]
Elevamos al cuadrado:
\[ \Rightarrow {\left( {x – 4} \right)^2} + {\left( {y – 3} \right)^2} \le {3^2}\]
Se trata de la ecuación del círculo (circunferencia y el interior) con centro en \(\left( {4,3} \right)\) y radio 3:
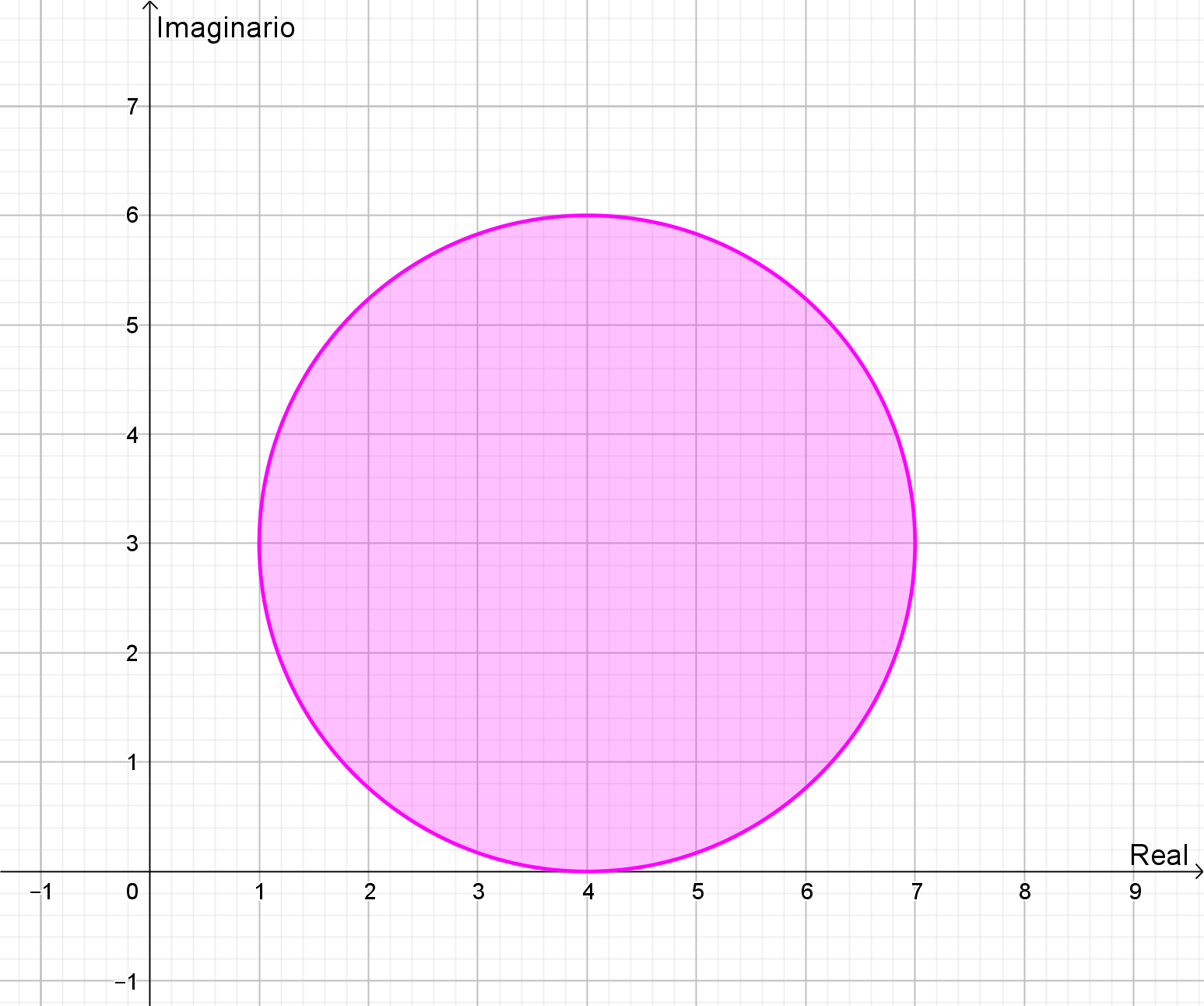
Si agregamos la condición \(Re\left( z \right) \le 4\):
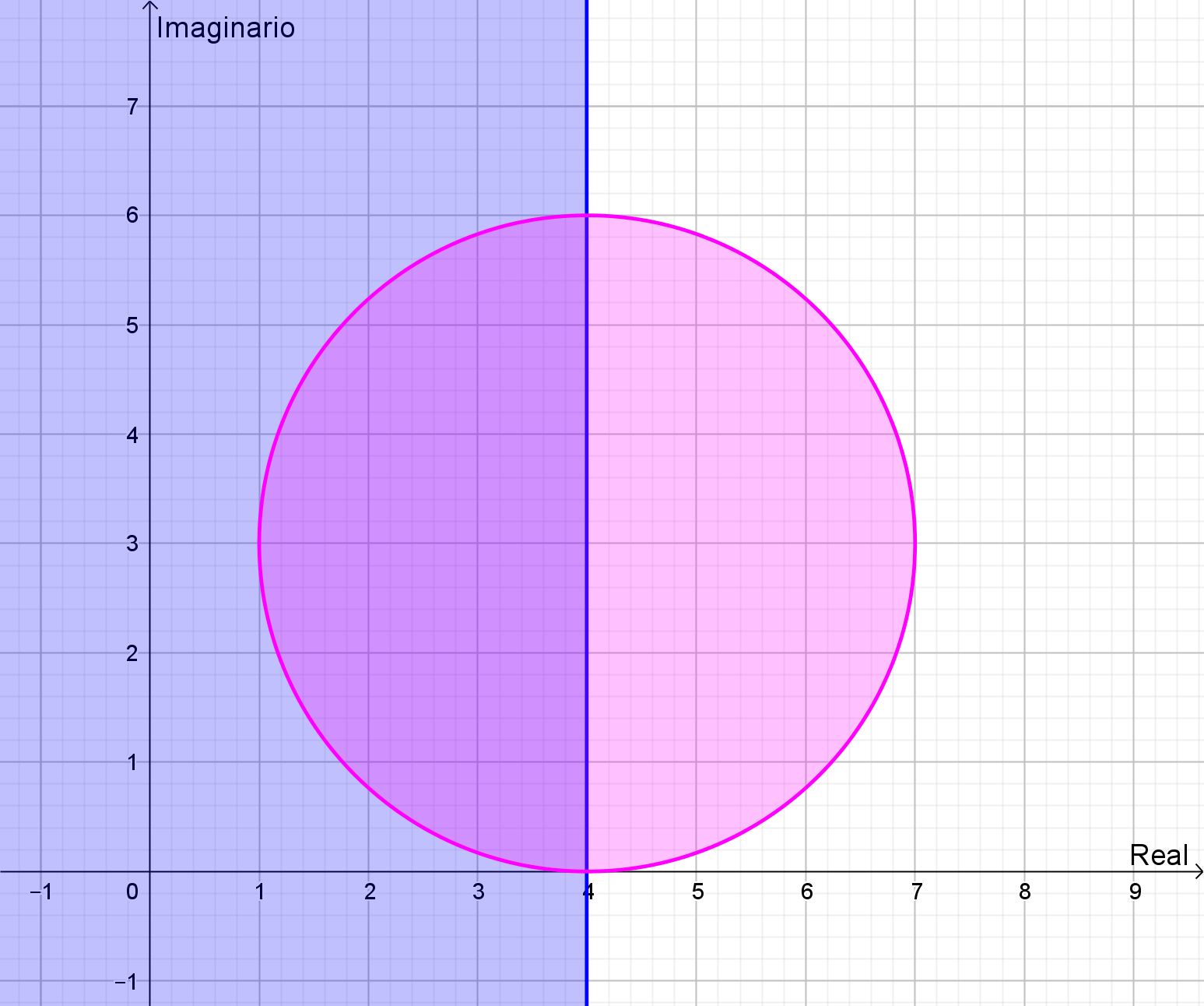
El conjunto de puntos del plano complejo que pertenece a la región doblemente sombreada (semi-circulo) es el que cumple con la expresión:
\(\left| {z – \left( {4 + 3i} \right)} \right| \le 3\) y \(Re\left( z \right) \le 4\) \(z \in \mathbb{C}\)

