Elipse

Definición y ecuación canónica de la elipse

\[\mathcal{E} = \left\{ {P\left( {x,y} \right)\;|\;d\left( {P,{F_1}} \right) + d\left( {P,{F_2}} \right) = cte} \right\}\]

A esa constante la llamamos \(2a\).

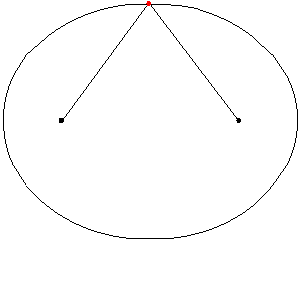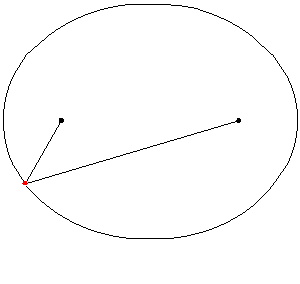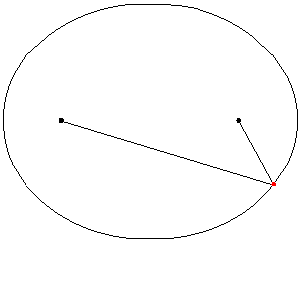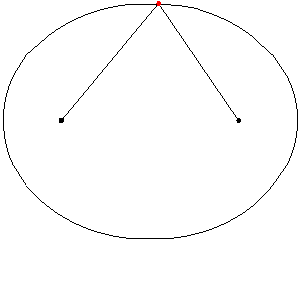
Consideremos que los focos son los puntos de coordenadas \({F_1}\left( { – c,0} \right)\) y \({F_2}\left( {c,0} \right)\) con \(c > 0\), y el punto medio entre los focos, se denomina centro \(C\left( {0,0} \right)\). En el siguiente esquema se pueden visualizar estos elementos:

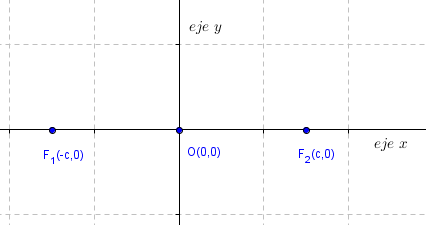
Si la distancia entre los focos es \(d\left( {{F_1},{F_2}} \right) = 2c\) , la condición para que sea una elipse es:

\[a > c > 0\]

Si elevamos al cuadrado:

\[{a^2} > {c^2}\]

A la diferencia se la llama \({b^2}\):

\[{a^2} – {c^2} = {b^2}\;\]

\[ \Rightarrow {a^2} = {b^2} + {c^2}\]

Haciendo una deducción se llega a:

Es la ecuación canónica de la elipse con centro \(\left( {0,0} \right)\) y eje focal \(y = 0\)(eje \(x\)).

Busquemos las intersecciones con los ejes:

Si \(y = 0\;:\;\;\) \(\;{x^2} = {a^2} \Rightarrow x = \pm a\;\; \Rightarrow {V_{1,2}} = \left( { \pm a,0} \right)\)

Si \(x = 0\;:\) \(\;\;\;{y^2} = {b^2} \Rightarrow y = \pm b\;\; \Rightarrow {V_{3,4}} = \left( {0, \pm b} \right)\)

Estos cuatro puntos se denominan vértices de la elipse.

• • \(a\) se denomina semieje mayor
  • \(b\) es el semieje menor
  • \(c\) es la semidistancia focal: (distancia del centro a un foco)
  • 2c es la distancia entre los focos
  • Eje focal: es la recta que pasa por los focos, en este caso el eje x

La gráfica representando todos estos elementos es la siguiente:

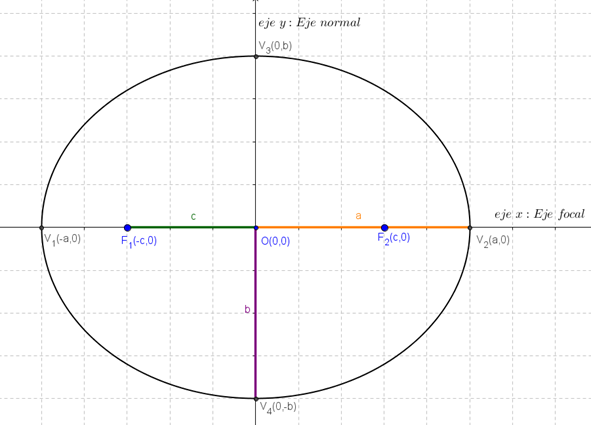
Observen que el centro es centro de simetría de la elipse.

Si en la ecuación canónica anterior permutamos x por y ( x\( \leftrightarrow \)y) queda:

Es la ecuación canónica de la elipse con centro\(\left( {0,0} \right)\) y eje focal \(x = 0\) (eje \(y\)).

En este caso las coordenadas de los vértices y focos son:

• • • Vértices: \({V_1}\left( {0,a} \right)\), \({V_2}\left( {0, – a} \right)\), \({V_3}\left( { – b,0} \right)\), \({V_4}\left( {b,0} \right)\)
    • Focos: \({F_1}\left( {0, – c} \right)\), \({F_2}\left( {0,c} \right)\)

Su gráfica es:

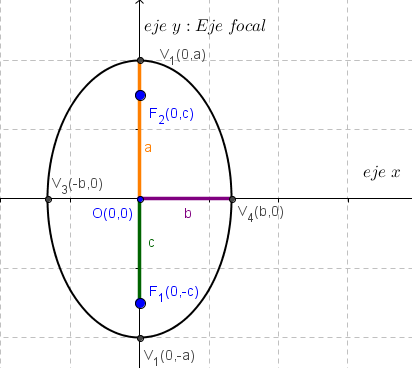
Excentricidad de una elipse

La excentricidad de una elipse se calcula como el cociente:

\[e = \frac{c}{a}\]

Donde \(a\) es el semieje mayor y \(c\) es la distancia del centro a uno de los focos.

Cómo \(0 < c < a\):

\[ \Rightarrow \;0 < \frac{c}{a} < 1\]

Por lo tanto la excentricidad de una elipse varía entre cero y uno.

En el siguiente archivo de GeoGebra pueden moverse los focos y un punto de la elipse para definirla. Además el programa calcula automáticamente la excentricidad.

Exploren cómo va cambiando la forma de la elipse en relación con la excentricidad.

Ejemplo 1

Hallar vértices, focos, eje focal, graficar y calcular excentricidad de la siguiente elipse:

\[\frac{{{x^2}}}{4} + \frac{{{y^2}}}{{10}} = 1\]

Resolución

Calculemos los valores de \(a\) y \(b\):

\[{a^2} = 10 \Rightarrow a = \sqrt {10} \]

\[{b^2} = 4 \Rightarrow b = 2\]

Entonces podemos dar las coordenadas de los vértices:

\[{V_1}\left( {0,\sqrt {10} } \right)\;\;;\;\;{V_2}\left( {0, – \sqrt {10} } \right)\;\;\;;\;\;\;{V_3}\left( {2,0} \right)\;\;\;;\;\;\;\;{V_4}\left( { – 2,0} \right)\;\;\]

Eje focal: es el eje \(y\), porque el denominador de \({y^2}\) es mayor que el denominador de \({x^2}\).

Para hallar las coordenadas de los focos necesitamos calcular \(c\):

\[{c^2} = {a^2} – {b^2} = 10 – 4 = 6\]

\[{F_1}\left( {0, – \sqrt 6 } \right)\;\;y\;\;{F_2}\left( {0,\sqrt 6 } \right)\]

Excentricidad de la elipse:

\[e = \frac{c}{a} = \frac{{\sqrt 6 }}{{\sqrt {10} }} = \sqrt {\frac{3}{5}} \]

La gráfica es:

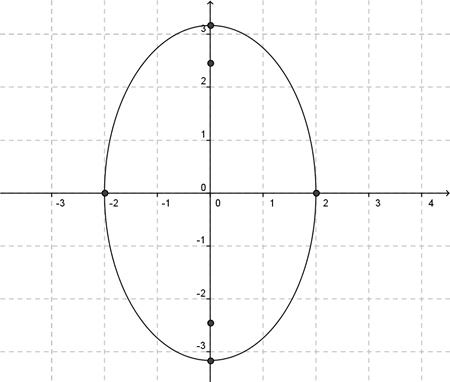
Ejemplo 2

Hallar la ecuación de una elipse con focos \({F_1}\left( {1, – 1} \right)\) y \({F_2}\left( {1,3} \right)\) y excentricidad \(\;e = 0,4\;.\)

Resolución

Empecemos graficando los focos y el centro:

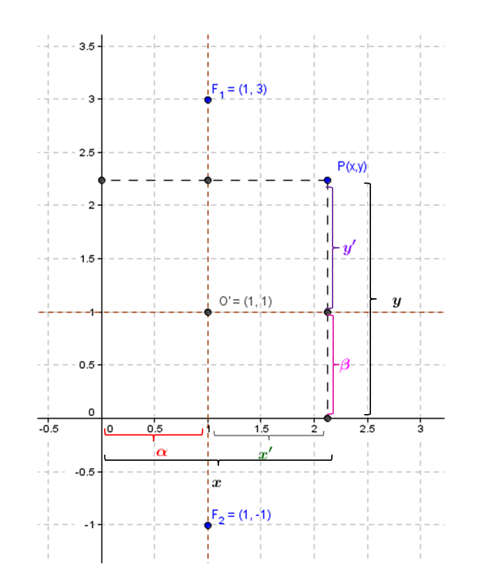
La elipse está corrida; no está centrada en \(\left( {0,0} \right)\). ¿Dónde está el centro de la elipse? En el punto medio de los dos focos \(C\left( {1,1} \right)\).

Pero podemos construir un sistema de ejes \(x’y’\) cuyo origen coincida con el centro de la elipse:

Ecuación del eje x’: \({\rm{\;}}y = 1\)

Ecuación del eje y’:\({\rm{\;\;}}x = 1\)

Hacemos una traslación de ejes:

\[\left\{ {\begin{array}{*{20}{c}}{x’ = x – \alpha }\\{y’ = y – \beta }\end{array}} \right.\;\;\]

Teniendo en cuenta las coordenadas del centro:

\[\;\;\left\{ {\begin{array}{*{20}{c}}{x’ = x – 1}\\{y’ = y – 1}\end{array}} \right.\;\]

Entonces en el nuevo sistema de ejes la ecuación quedaría:

\[\frac{{{{y’}^2}}}{{{a^2}}} + \frac{{{{x’}^2}}}{{{b^2}}} = 1\]

Recordemos que \(c\) es la distancia de un foco al centro, así que:

\[c = 2\]

Y conocemos además que la excentricidad es 0,4

\[e = \frac{c}{a}\]

Entonces despejamos de esta expresión \(a\):

\[a = \frac{c}{e} = \frac{2}{{0,4}} = 5\; \Rightarrow {a^2} = 25\]

Calculamos \(b\):

\[{b^2} = 25 – 4 = 21 \Rightarrow b = \sqrt {21} \]

Y ahora volvemos al sistema original

\[\frac{{{{\left( {y – 1} \right)}^2}}}{{25}} + \frac{{{{\left( {x – 1} \right)}^2}}}{{21}} = 1\]

En la siguiente tabla resumimos las coordenadas del centro, focos y vértices en ambos sistemas de referencia:

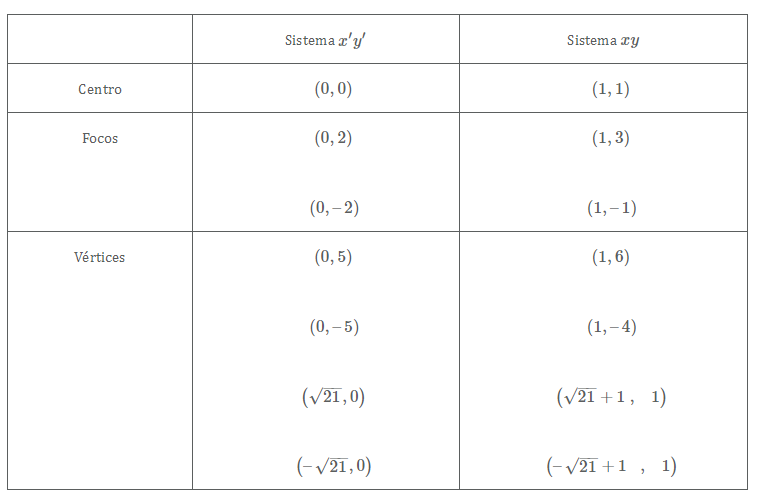
La gráfica queda:

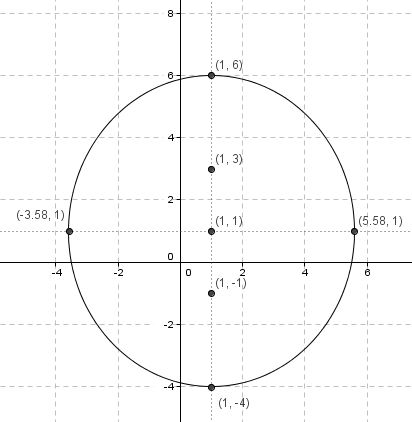
Ecuación ordinaria de una elipse con \(C\left( {\alpha ,\beta } \right)\)

Si el eje focal es horizontal la ecuación ordinaria es:

\[\frac{{{{\left( {x – \alpha } \right)}^2}}}{{{a^2}}} + \frac{{{{\left( {y – \beta } \right)}^2}}}{{{b^2}}} = 1\]

Si el eje focal es vertical la ecuación ordinaria es:

\[\frac{{{{\left( {y – \beta } \right)}^2}}}{{{a^2}}} + \frac{{{{\left( {x – \alpha } \right)}^2}}}{{{b^2}}} = 1\]

Noten que como \(a > b\), la única diferencia entre las dos ecuaciones consiste en que \({a^2}\) está en el denominador de \(x\) o de \(y\).

Ejemplo 3

Hallar la ecuación ordinaria de la curva definida por:

\[{x^2} + 2{y^2} + 2x – 8y + 7 = 0\]

Graficar.

Resolución

Como el coeficiente de \({x^2}\) y de \({y^2}\) no son el mismo, no puede tratarse de una circunferencia. Tampoco de una parábola porque ninguno de los dos coeficientes es igual a cero. Tampoco de una hipérbola porque tienen el mismo signo. Así que inicialmente esperamos que sea una elipse.

Completemos cuadrados:

\[{x^2} + 2x + 2.\left( {{y^2} – 4y} \right) + 7 = 0\]

\[{\left( {x + 1} \right)^2} – {1^2} + 2.\left[ {{{\left( {y – 2} \right)}^2} – 4} \right] + 7 = 0\]

\[{\left( {x + 1} \right)^2} + 2.{\left( {y – 2} \right)^2} – 1 – 8 + 7 = 0\]

\[{\left( {x + 1} \right)^2} + 2.{\left( {y – 2} \right)^2} = 2\]

\[\frac{{{{\left( {x + 1} \right)}^2}}}{2} + {\left( {y – 2} \right)^2} = 1\]

Llegamos a la ecuación ordinaria de una elipse con centro en \(\left( { – 1,2} \right)\) y eje focal horizontal (porque el semieje mayor es \(a = \sqrt 2 \) que está en el denominador de \(x\), y el semieje menor es \(b = 1\), está en el denominador de \(y\)). Calculemos \(c\):

\[{c^2} = {a^2} – {b^2} = 2 – 1 = 1\]

Si quisiéramos obtener la ecuación canónica deberíamos establecer las ecuaciones de traslación:

\[\left\{ {\begin{array}{*{20}{c}}{x’ = x + 1}\\{y’ = y – 2}\end{array}\; \Rightarrow \;\;\left\{ {\begin{array}{*{20}{c}}{x = x’ – 1}\\{y = y’ + 2}\end{array}} \right.} \right.\]

\[\frac{{{{x’}^2}}}{2} + {y’^2} = 1\]

Resumamos la información obtenida en los dos sistemas de ejes: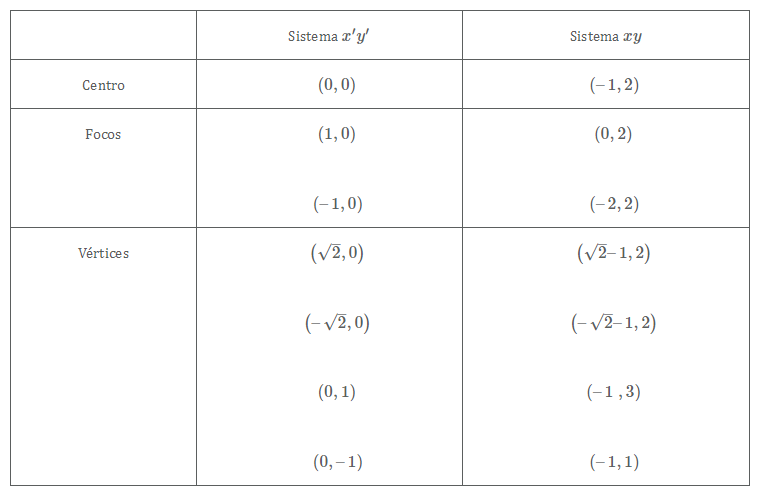

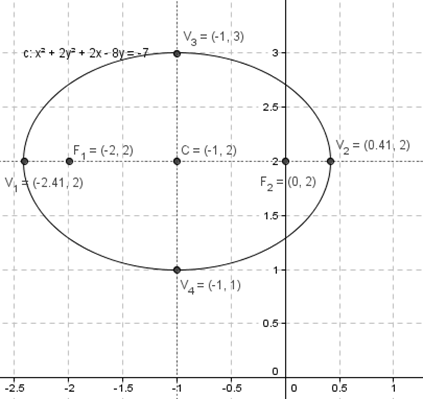
Finalmente podemos hacer la gráfica de la elipse con todos sus elementos:

Videos relacionados