A continuación veremos una serie de ejemplos que muestran cómo se puede graficar una región del plano complejo que cumple con ciertas condiciones.
Ejemplo 1
Hallar la región del plano complejo determinada por:
\[\left\{ {z \in \mathbb{C}\;:\;\;\;\left| {z + 2} \right| \le 1} \right\}\]
Resolución
Si \(z = x + yi\) , resulta:
\[\left| {x + yi + 2} \right| \le 1\]
\[\left| {\left( {x + 2} \right) + yi\;} \right| \le 1\]
\[\sqrt {{{\left( {x + 2} \right)}^2} + {y^2}} \le 1\]
Observación importante: La unidad imaginaria no interviene en el cálculo del módulo:
\[\left| {a + bi} \right| = \sqrt {{a^2} + {b^2}} \]
Elevando al cuadrado ambos miembros:
\[{\left( {x + 2} \right)^2} + {y^2} \le 1\]
Podemos sustituir el símbolo de \( \le \) por el de \( = \) para obtener la frontera o borde de la región:
\[{\left( {x + 2} \right)^2} + {y^2} = 1\]
Ésta es la ecuación de una circunferencia con centro en \(\left( { – 2,0} \right)\) y radio 1.
Veamos una gráfica de la región:
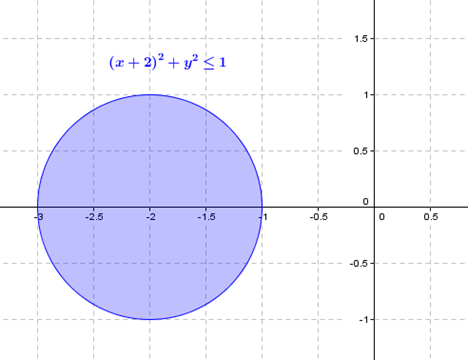
Son todos los puntos que están a distancia menor o igual que 1 del punto (-2,0)
Ejemplo 2
Hallar la región del plano complejo determinada por:
\[\left\{ {z \in \mathbb{C}\;\;:\;\;\;\left| z \right| \le 2\;\;,\;\;\frac{\pi }{2} \le \arg \left( z \right) \le \frac{3}{4}\pi } \right\}\]
Resolución
Esta región está definida utilizando la expresión trigonométrica de un número complejo. \(\left| z \right| \le 2\) quiere decir que el módulo debe ser menor o igual a 2, y la otra condición establece que el argumento está entre \(\pi /2\) y \(3/4\pi \).
Luego:
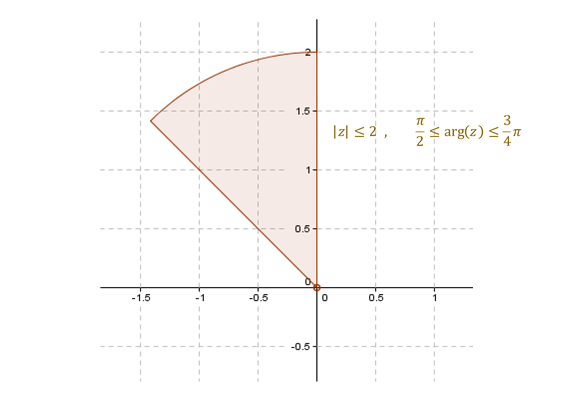
Observación: \(z = \left( {0,0} \right)\) no está incluido, porque no tiene argumento.
Ejemplo 3
Hallar la región del plano complejo determinada por:
\(\left\{ {z \in \mathbb{C}\;\;:\;\;\;\left| {z + i} \right| \le 2\;\;,\;\;\frac{\pi }{2} \le \arg \left( z \right) \le \frac{3}{4}\pi } \right\}\)
Resolución
Esta región está definida utilizando la expresión trigonométrica de un número complejo. \(\left| {z + i} \right| \le 2\)representa al círculo con centro en \( – i\) de radio 2. La otra condición establece que el argumento está comprendido entre \(\pi /2\) y \(3/4\pi \).
Luego la intersección entre ambas regiones es:
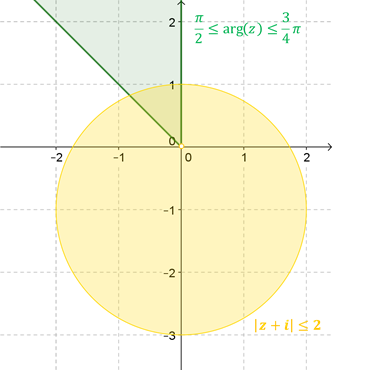
Noten que \(z = 0\) no está incluido porque no tiene argumento.
Observación: un error muy común es indicar el ángulo dado por \(\frac{\pi }{2} \le \arg \left( z \right) \le \frac{3}{4}\pi \) con vértice en el centro de la circunferencia:
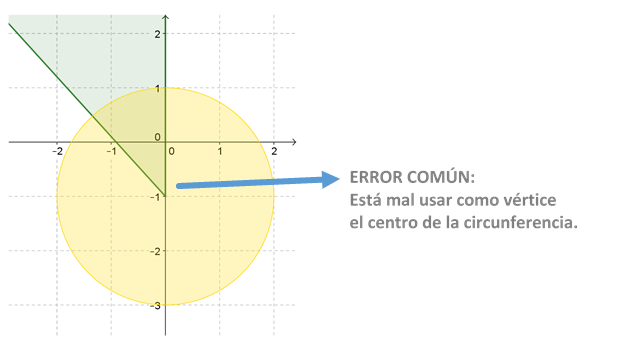
Ejemplo 4
\[\left\{ {z \in \mathbb{C}\;:\;\;\;\left| {z + i} \right| = \left| {z – 1} \right|\;\;,\;\;Re\left( z \right) > 1} \right\}\]
Resolución
Razonamiento analítico
\[\left| {x + iy + i} \right| = \left| {x + iy – 1} \right|\]
\[\left| {\;x + i\left( {y + 1} \right)} \right| = \left| {\;\left( {x – 1} \right) + iy\;} \right|\]
Calculamos el módulo de cada complejo:
\[\sqrt {{x^2} + {{\left( {y + 1} \right)}^2}} = \sqrt {{{\left( {x – 1} \right)}^2} + {y^2}} \;\;\;\;\;,\;\;\;\;\;x > 1\]
\[{x^2} + {\left( {y + 1} \right)^2} = {\left( {x – 1} \right)^2} + {y^2}\;\;\;\;,\;\;\;\;\;x > 1\]
\[{x^2} + {y^2} + 2y + 1 = {x^2} – 2x + 1 + {y^2}\;\;\;\;\;,\;\;\;\;\;x > 1\]
\[2y + 1 = – 2x + 1\;\;\;\;\;\;,\;\;\;\;\;x > 1\]
\[y = – x\;\;\;,\;\;x > 1\]
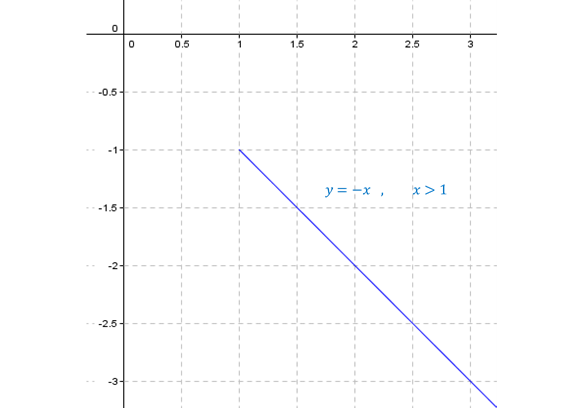
Interpretación geométrica
Si \(a,b \in \mathbb{R}\) entonces \(\left| {a – b} \right|\) representa la distancia entre \(a\) y \(b\).
Análogamente se puede definir la distancia en \(\mathbb{C}\). Sean \({z_1},{z_2} \in \mathbb{C}\) entonces \(\left| {{z_1} – {z_2}} \right|\) es la distancia entre \({z_1}\) y \({z_2}\).
Luego \(\left| {z + i} \right| = \left| {z – \left( { – i} \right)} \right|\)representa la distancia entre \(z\) y \( – i\).
Y \(\left| {z – 1} \right|\) representa la distancia entre \(z\) y \(1\).
La ecuación\(\left| {z + i} \right| = \left| {z – 1} \right|\)caracteriza al conjunto de números complejos que están a igual distancia de\(\left( { – i} \right)\) que de \(1\).
Traducido a \({\mathbb{R}^2}\), se trata del conjunto de puntos del plano que equidistan de \(A\left( {0,\; – 1} \right)\) y \(B\left( {1,0} \right)\), o sea, es la mediatriz del segmento \(AB\). Considerando la restricción \(Re\left( z \right) > 1\), se obtiene la gráfica anterior.
Ejemplo 5
Hallar la región del plano complejo determinada por:
\[Im\left( {z – i} \right) = Re\left( {z + 1} \right)\]
Resolución
Escribiremos al número complejo \(z\) como \(x + yi\):
\[Im\left( {x + iy – i} \right) = Re\left( {x + iy + 1} \right)\]
\[y – 1 = x + 1\]
\[y = x + 2\]
Veamos una gráfica de la región (que es sencillamente la recta \(y = x + 2)\):
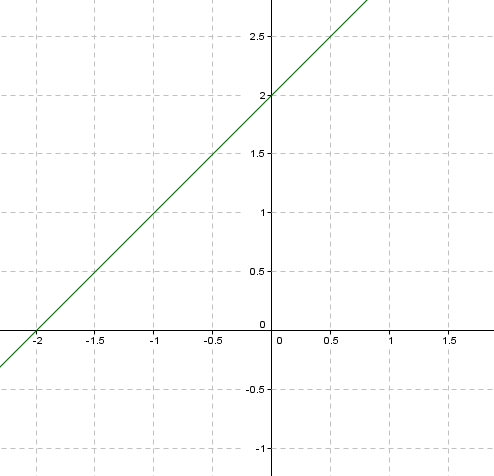
Ejemplo 6
Hallar la región del plano complejo determinada por:
\[\left\{ {\begin{array}{*{20}{c}}{\left| {z – i} \right| + \left| {z + i} \right| = 4}\\{0 \le Arg\left( z \right) \le \pi }\end{array}} \right.\]
Resolución
\[\left| {x + yi – i} \right| + \left| {x + yi + i} \right| = 4\]
\[\sqrt {{x^2} + {{\left( {y – 1} \right)}^2}} + \sqrt {{x^2} + {{\left( {y + 1} \right)}^2}} = 4\]
\[\sqrt {{x^2} + {{\left( {y – 1} \right)}^2}} = 4 – \sqrt {{x^2} + {{\left( {y + 1} \right)}^2}} \]
Elevamos al cuadrado a ambos miembros:
\[{x^2} + {\left( {y – 1} \right)^2} = {4^2} + {x^2} + {\left( {y + 1} \right)^2} – 8\sqrt {{x^2} + {{\left( {y + 1} \right)}^2}} \]
\[{y^2} – 2y + 1 = {4^2} + {y^2} + 2y + 1 – 8\sqrt {{x^2} + {{\left( {y + 1} \right)}^2}} \]
\[ – 4y – 16 = – 8\sqrt {{x^2} + {{\left( {y + 1} \right)}^2}} \]
\[\frac{{y + 4}}{2} = \sqrt {{x^2} + {{\left( {y + 1} \right)}^2}} \]
Volvemos a elevar al cuadrado a ambos miembros:
\[{\frac{{\left( {y + 4} \right)}}{4}^2} = {x^2} + {\left( {y + 1} \right)^2}\]
\[{\left( {y + 4} \right)^2} = 4{x^2} + 4{\left( {y + 1} \right)^2}\]
\[{y^2} + 8y + 16 = 4{x^2} + 4{y^2} + 8y + 4\]
\[0 = 4{x^2} + 3{y^2} – 12\]
\[12 = 4{x^2} + 3{y^2}\}
\[\frac{{{x^2}}}{3} + \frac{{{y^2}}}{4} = 1\]
Se trata de la ecuación de una elipse con eje focal vertical y centrada en \(\left( {0,0} \right)\):
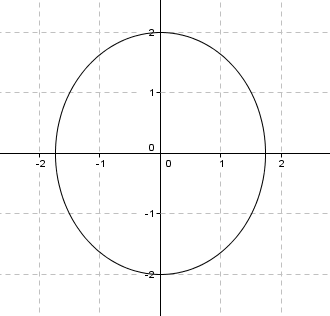
Pero también debe ser:
\[0 \le Arg\left( z \right) \le \pi \]
Luego no es toda la elipse sino aquel arco que cumple con que el argumento está comprendido entre 0 y \(\pi \):
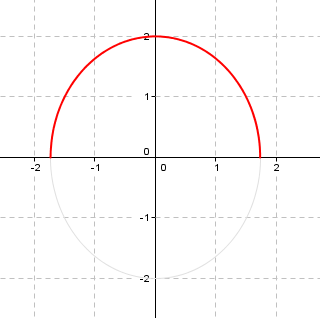
Interpretación geométrica
\[\left\{ {\begin{array}{*{20}{c}}{\left| {z – i} \right| + \left| {z + i} \right| = 4}\\{0 \le Arg\left( z \right) \le \pi }\end{array}} \right.\]
\(\left| {z – i} \right|\): representa la distancia de\(\;\;z\) a \(i\)
\(\left| {z + i} \right|\): representa la distancia de \(\;z\) a -\(i\)
Es decir que la suma de esas distancias debe ser constante, e igual a 4.
Traducido a \({\mathbb{R}^2}\), es el conjunto de puntos del plano tales que la suma de sus distancias a dos puntos fijos: \(\left( {0,1} \right)\) y \(\left( {0,\; – 1} \right)\) es igual a 4. De acuerdo con lo que hemos visto en la unidad de cónicas, se trata de la elipse de focos \(\left( {0,1} \right)\) y \(\left( {0,\; – 1} \right)\) y semieje mayor \(a\; = \;2\).
Para hallar el semieje menor aplicamos la relación: \({a^2} = {b^2} + {c^2}\) , a partir de la cual se obtiene \(b = \sqrt 3 \) .
Ejercicio para el lector 5
Hallar analíticamente y graficar la región del plano complejo definida por:
\[\{ z \in C:\;\;\left| {z – 2i} \right| < 2\;\;,\;\;Im\left( {{z^2}} \right) \le 0\;\;,\;\;\;\frac{\pi }{4} \le \arg \left( z \right) \le \frac{{3\pi }}{4}\;\;\} \]
Videos relacionados con regiones del plano complejo

