Radicación de números complejos

Criterio de igualdad de números complejos

Sean \({z_1}\; = \;a\; + \;bi\;\) y \({z_2}\; = \;c\; + \;di\)

¿Cuándo son iguales?

\[{z_1} = {z_2}\;\;\; \Leftrightarrow \;\;\;\;a = c\; \wedge \;\;b = d\]

Si los números complejos están dados en forma trigonométrica, ¿qué condiciones deben cumplirse para que sean iguales?

Consideremos este ejemplo:

\[{z_1} = 8\;(\cos (\pi ) + i\;sen\left( \pi \right))\;\;\;\;,\;\;\;\;{z_2} = 8\;(\cos (3\pi ) + i\;sen\left( {3\pi } \right))\]

Observamos que tienen el mismo módulo pero diferentes argumentos. Sin embargo, silos traducimos a forma binómica resulta: \({z_1} = {z_2} = – 8\)

Teniendo en cuenta que un número complejo tiene infinitos argumentos:

\[\arg \left( z \right) = Arg\left( z \right) + 2k\pi \;\;\;,\;\;\;\;k \in \mathbb{Z}\]

puede establecerse el siguiente criterio de igualdad de números complejos:

Sean

\[{z_1} = \left| {{z_1}} \right|.\left( {\cos \alpha + i.sen\;\alpha } \right)\]

\[{z_2} = \left| {{z_2}} \right|.\left( {\cos \beta + i.sen\;\beta } \right)\]

\[{z_1} = {z_2}\;\;\; \Leftrightarrow \;\;\;\left\{ {\begin{array}{*{20}{c}}{\left| {{z_1}} \right| = \left| {{z_2}} \right|}\\{\;\alpha – \beta = 2k\pi \;\;,\;\;\;k \in Z}\end{array}} \right.\]

Ejemplo: \(3\;cis\left( {\frac{\pi }{4}} \right) = 3\;cis\left( { – \frac{{7\pi }}{4}} \right) = 3\;cis\;\left( {\frac{{17\pi }}{4}\;} \right)\)

El mismo criterio se aplica para la forma exponencial.

Ejemplo introductorio

Consideremos la siguiente ecuación:

\[{x^4} + 1 = 0\]

Esta ecuación no tiene solución en \(\mathbb{R}\). Sin embargo, hay un notable teorema que nos permite asegurar que sí tiene solución en \(\mathbb{C}\). Es el teorema fundamental del Álgebra, que afirma:

Es decir que la ecuación dada tiene exactamente 4 soluciones en \(\mathbb{C}\).

Despejemos \(x\) en la ecuación \(\;\;{x^4} + 1 = 0\)

\[{x^4} = – 1\]

\[x = \sqrt[4]{{ – 1}}\]

Veremos a continuación cómo obtener las raíces de un número complejo.

Radicación

Dado \(z = \left| z \right|{e^{i\alpha }}\), queremos calcular \(\sqrt[n]{z}\) que llamaremos\(w\).

\(\sqrt[n]{z} = w\;\; \Leftrightarrow \;{w^n} = z\)

Si expresamos \(w\) en forma exponencial:

\[w = \left| w \right|{e^{i\beta }}\]

Resulta, de acuerdo con la fórmula de potenciación:

\[{w^n} = {\left| w \right|^n}{e^{in\beta }}\]

\[{w^n} = z \Leftrightarrow \;{\left| w \right|^n}{e^{in\beta }} = \left| z \right|{e^{i\alpha }}\]

Teniendo en cuenta que:

\[{z_1} = {z_2}\; \Leftrightarrow \;\;\left\{ {\begin{array}{*{20}{c}}{\left| {{z_1}} \right| = \left| {{z_2}} \right|}\\{\arg \left( {{z_1}} \right) – \arg \left( {{z_2}} \right) = 2k\pi \;\;\;k \in Z}\end{array}} \right.\]

Resulta:

\[{w^n} = z \Leftrightarrow \;\;\left\{ {\begin{array}{*{20}{c}}{{{\left| w \right|}^n} = z\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( 1 \right)}\\{n\beta  – \alpha  = 2k\pi \;\;\;,\;\;\;k \in Z\;\;\;\;\;\;\;\left( 2 \right)}\end{array}} \right.\]

De \(\left( 1 \right)\) se deduce:

\[\left| w \right| = \sqrt[n]{{\left| z \right|}}\]

De \(\left( 2 \right)\)se deduce:

\[\beta = \frac{{\alpha + 2k\pi }}{n}\;\;,\;\;\;k \in \mathbb{Z}\]

Por lo tanto si \(z = \left| z \right|{e^{i\alpha }}\):

\[\sqrt[n]{z} = \sqrt[n]{{\left| z \right|}}.{e^{i\left( {\frac{{\alpha + 2k\pi }}{n}} \right)}}\;\;\;\;,\;\;\;\;k \in \mathbb{Z}\]

Ejemplo 1

Calcular\(\sqrt[3]{{ – 1 – i}}\).

Resolución

\[z = – 1 – i\;\;\;\;,\;\;\;\;\;\left| z \right| = \sqrt 2 \;\;\;\;\;,\;\;\;\;Arg\left( z \right) = \frac{5}{4}\pi \]

\[k = 1\;\;\; \Rightarrow \;\;{w_1} = \sqrt[6]{2}.{e^{\frac{{13}}{{12}}\pi i}}\]

\[k = 2\;\;\; \Rightarrow \;\;{w_2} = \sqrt[6]{2}.{e^{\frac{{21}}{{12}}\pi i}}\]

\(k = 3 \Rightarrow {w_3} = \sqrt[6]{2}.{e^{\frac{{29}}{{12}}\pi i}}\)    ,      \(\frac{{29}}{{12}}\pi  = 2\pi  + \frac{5}{{12}}\pi \)   ,   \({w_3}\) coincide con \({w_0}\)

\(k = 4 \Rightarrow {w_4} = \sqrt[6]{2}.{e^{\frac{{37}}{{12}}\pi i}}\)     ,      \(\frac{{37}}{{12}}\pi  = 2\pi  + \frac{{13}}{{12}}\pi \)  ,    \({w_4}\) coincide con \({w_1}\)

\(k = 5 \Rightarrow {w_5} = \sqrt[6]{2}.{e^{\frac{{45}}{{12}}\pi i}}\)     ,       \(\frac{{45}}{{12}}\pi  = 2\pi  + \frac{{21}}{{12}}\pi \)  ,     \({w_5}\) coincide con  \({w_2}\)

Las soluciones empiezan a repetirse. Hemos encontrado tres soluciones distintas: \({w_0},{w_1}\) y \({w_2}\). Realicemos una gráfica con estas tres soluciones:

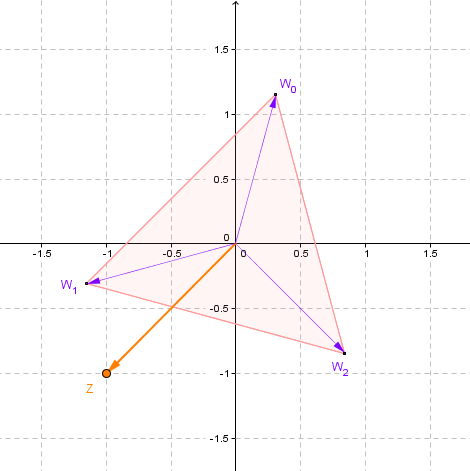
Cómo se puede ver en la gráfica, las tres raíces cúbicas de \(z\) forman un triángulo equilátero.

Retomemos la fórmula de radicación y analicemos cuántas soluciones distintas se obtienen.

Para \(z = \left| z \right|{e^{i\alpha }}\) , habíamos obtenido:

\[\sqrt[n]{z} = \sqrt[n]{{\left| z \right|}}.{e^{i\left( {\frac{{\alpha + 2k\pi }}{n}} \right)}}\;\;\;\;,\;\;\;\;k \in \mathbb{Z}\]

Asignando valores a \(k\):

\[k = 0\;\; \Rightarrow \;\;\;{\beta _0} = \frac{\alpha }{n}\]

\[k = 1\;\; \Rightarrow \;\;\;{\beta _1} = \frac{{\alpha + 2\pi }}{n}\]

\[k = 2\;\; \Rightarrow \;\;\;{\beta _2} = \frac{{\alpha + 2.\left( {2\pi } \right)}}{n}\]

\[k = 3\;\; \Rightarrow \;\;\;{\beta _3} = \frac{{\alpha + 3.\left( {2\pi } \right)}}{n}\]

\[ \vdots \]

\[k = n – 1\;\; \Rightarrow \;\;\;{\beta _{n – 1}} = \frac{{\alpha + \left( {n – 1} \right).\left( {2\pi } \right)}}{n}\]

\[k = n\; \Rightarrow \;\;\;{\beta _n} = \frac{{\alpha + n.\left( {2\pi } \right)}}{n} = \frac{\alpha }{n} + 2\pi = {\beta _0}\]

\[k = n + 1 \Rightarrow \;\;\;{\beta _{n + 1}} = \frac{{\alpha + \left( {n + 1} \right).\left( {2\pi } \right)}}{n} = \frac{{\alpha + 2\pi }}{n} + 2\pi = {\beta _1}\]

\[ \vdots \]

Vemos que a partir de \(k = n\), empiezan a repetirse las soluciones.

Podemos concluir que las soluciones distintas se obtienen con \(k = 0,1, \ldots ,\;n – 1\). Por lo tanto, la raíz enésima de un número complejo tiene exactamente \(n\) soluciones:

Notemos que las \(n\) raíces tienen el mismo módulo. Tal como vimos en el ejemplo 1, podemos afirmar que las \(n\) raíces enésimas de un número complejo forman un polígono regular de n lados inscripto en una circunferencia de radio \(\sqrt[n]{{\left| z \right|}}\).

Ejercicio para el lector 2

Completar la siguiente tabla:

Ejemplo 2

Resolver en \(\mathbb{C}\) la siguiente ecuación:

\[{x^4} + 1 = 0\]

Resolución

Despejando:

\[x = \sqrt[4]{{ – 1}}\]

Luego debemos buscar la raíz cuarta de \(z = – 1 = {e^{\pi \;i}}\). Según la fórmula de radicación:

\[x = \sqrt[4]{1}{e^{\left( {\frac{{\pi + 2k\pi }}{4}} \right)\;i}}\;\;,\;\;\;k = 0,1,2,3\;\]

\[ \Rightarrow {x_0} = {e^{\frac{\pi }{4}\;i}}\]

\[ \Rightarrow {x_1} = {e^{\frac{{3\pi }}{4}\;i}}\]

\[ \Rightarrow {x_2} = {e^{\frac{{5\pi }}{4}\;i}}\]

\[ \Rightarrow {x_3} = {e^{\frac{{7\pi }}{4}\;i}}\]

Grafiquemos estas cuatro soluciones obtenidas:

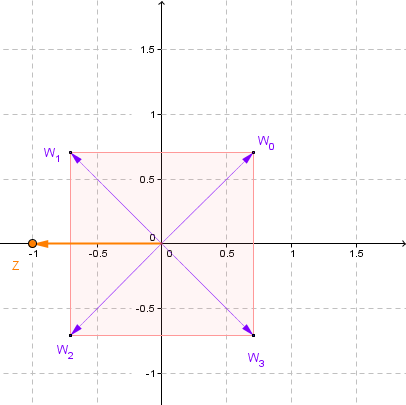
También se forma un polígono regular con las raíces cuartas de \(z\), en este caso se trata de un cuadrado.

Applet de GeoGebra para explorar la «geometría» de las raicés n-ésimas de un número complejo

En el siguiente applet es posible calcular y graficar las raíces enésimas de un número complejo dado. Está configurado para realizar raíces de índice entre 2 hasta 8.

Se puede definir un complejo \(z\) en forma binómica completando los casilleros, o bien tomar con el cursor un punto del plano.

El índice de la raíz se puede seleccionar desde \(n = 2\) hasta \(n = 8\) moviendo el punto sobre el segmento.

Les proponemos que elijan diferentes números complejos y calculen raíces de distintos índices.

Como habíamos visto anteriormente el gráfico de las raíces de un número complejo es un polígono regular de \(n\) lados que está inscripto en una circunferencia de radio \(\sqrt[n]{{\left| z \right|}}\).

Este applet puede usarse para verificar los resultados obtenidos en algunos ejercicios (por ejemplo en el EPL 2).

Ejemplo 3

Resolver la siguiente ecuación \(\mathbb{R}\) y \(\mathbb{C}\):

\[{x^5} + 16x = 0\]

Resolución

En \(\mathbb{R}\):

Factoreando:

\[x\left( {{x^4} + 16} \right) = 0\]

\[ \Rightarrow \;x = 0\;\; \vee \;\;\;{x^4} + 16 = 0\]

La segunda ecuación no tiene solución en reales, luego:

\[{S_\mathbb{R}} = \left\{ 0 \right\}\]

En \(\mathbb{C}\):

En \(\mathbb{C}\) hay cuatro soluciones para la ecuación \({x^4} + 16 = 0\), que son las raíces cuartas de \( – 16\). Luego la solución es de la forma:

\[{S_\mathbb{C}} = \left\{ {0;{w_0};{w_1},{w_2},{w_3}} \right\}\]

Donde \({w_0},{w_1},{w_2}\) y \({w_3}\) son las raíces cuartas de \( – 16\). Dejamos a cargo del lector el cálculo de las mismas.

Ejercicio para el lector 3

Hallar \(z \in \mathbb{C}\) sabiendo que \(w = \sqrt 3 – i\) es una de las raíces cúbicas de z. Obtener y graficar el conjunto de raíces cúbicas de z.

Ejercicio para el lector 4

Resolver en \(\mathbb{R}\)y en \(\mathbb{C}\)la ecuación\(\left( {{x^2} + 3} \right)\left( {{x^3} + k} \right) = 0\)sabiendo que \(x = 2{e^{\frac{\pi }{3}i}}\)es una de las soluciones.

Videos relacionados con radicación de números complejos