Producto vectorial y mixto

Producto vectorial

Definición

Para resolver numerosos problemas de Geometría, Física e Ingeniería, interesa construir un vector en \({\mathbb{R}^3}\) que sea perpendicular a dos vectores dados.

O sea: dados \(\vec u,\vec v \in {\mathbb{R}^3}\), nos proponemos hallar un vector \(\vec w\) tal que \(\vec w \bot \vec u\) y \(\;\overrightarrow {\;w} \bot \vec v\).

El producto vectorial es una operación entre vectores que facilita la obtención de \(\vec w\).

Definición: El producto vectorial de \(\vec u\;\;y\;\;\vec v\), que indicaremos \(\vec u \times \vec v\) , es un vector

\[\vec u \times \vec v = \vec w\]

Que tiene:

• Dirección perpendicular a \(\vec u\) y a \(\vec v\): \(\;\;\vec w \bot \vec u\;\; \wedge \;\;\vec w \bot \vec v\)
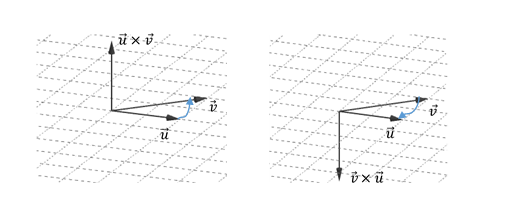
• Sentido: regla de la mano derecha: si con la mano derecha se recorre el menor ángulo posible entre \(\vec u\) y \(\vec v\), el pulgar indica el sentido de \(\vec w\)

• Módulo:

\[\lVert \vec w\rVert = \lVert \vec u\rVert\;\lVert \vec v\rVert\;sen\left( \theta \right)\]

siendo \(\theta \;\;\)el ángulo comprendido entre \(\vec u\;\;y\;\;\vec v\)

Se puede ver que no es una operación conmutativa porque si cambiamos el orden de los vectores, se conservan la dirección y el módulo del producto vectorial pero se invierte su sentido:

\[\vec u \times \vec v = – \left( {\vec v \times \vec u} \right)\]

Ejemplo

\[\vec a = \left( {0,1, – 1} \right)\]

\[\vec b = \left( {0,0,3} \right)\]

Hallar el vector \(\vec a \times \vec b\).

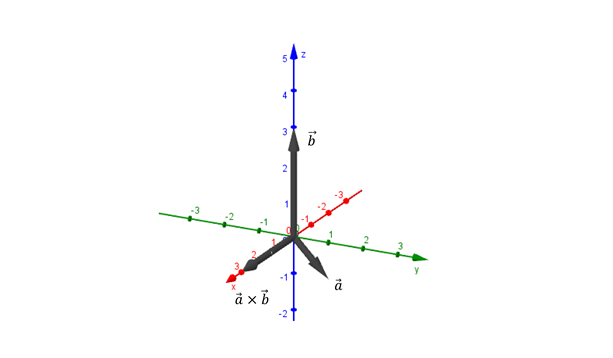
Dirección: eje \(x\)

Sentido: semieje positivo de \(x\)

Módulo: \(\sqrt 2 .3.sen\left( {135^\circ } \right) = \sqrt 2 .3.\frac{{\sqrt 2 }}{2} = 3\;\;\)

Entonces:

\[\vec a \times \vec b = \left( {3,0,0} \right)\]

Propiedades del producto vectorial

1. \(\vec u \times \vec v = – \left( {\vec v \times \vec u} \right)\)
2. \(\left( {u + v} \right) \times w = \vec u \times \vec w + \vec v \times \vec w\)
3. \(\left( {k\vec u} \right) \times \vec v = k\left( {\vec u \times \vec v} \right) = \vec u\; \times \;\left( {k\vec v} \right)\)
4. \(\vec v \times \vec v = \vec 0\;,\;\;pues\;\;\;\lVert \vec v \times \vec v\rVert = \lVert \vec v\rVert\;\lVert \vec v\rVert\;sen\left( 0 \right) = 0\)
5. \(\vec u\parallel \vec v\; \Rightarrow \;\vec u \times \vec v = \vec 0\;,\;\;\;pues\;\;\;sen\left( {0^\circ } \right) = sen\left( {180^\circ } \right) = 0\)
6. \(\vec 0\;x\;\vec v\; = \;\vec v\;x\;\vec 0\; = \;\vec 0\)

Si \(\vec u\) y \(\overrightarrow {\;v} \) son vectores no nulos, podemos enunciar una condición necesaria y suficiente de paralelismo:

\[\vec u\parallel \vec v\;\; \Leftrightarrow \;\vec u \times \vec v = \vec 0\;\; \Leftrightarrow \;\vec u = k\vec v\;\;\;con\;\;k\; \in {\mathbb{R}}\]

Ejercicio para el lector 2

A partir de las características del producto vectorial podemos calcular los productos vectoriales de los versores canónicos. Por ejemplo:

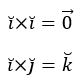
Le proponemos al lector que calcule los restantes productos vectoriales de los versores canónicos:

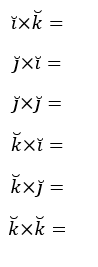
Fórmula para calcular el producto vectorial

Dados \(\vec u = \left( {{u_x},{u_y},{u_z}} \right)\) y \(v = \left( {{v_x},{v_y},{v_z}} \right)\) podemos hallar una fórmula para el producto vectorial expresando los vectores en forma canónica:

Aplicando propiedades del producto vectorial y considerando los productos entre los versores canónicos, se obtiene la siguiente fórmula:

Esta fórmula puede expresarse en forma más sencilla utilizando determinantes, tema que presentaremos brevemente y luego desarrollaremos en la próxima unidad.

Una matriz es un ordenamiento rectangular de números, como caso particular nos interesan las matrices cuadradas (igual número de filas y de columnas).

\(A = \left( {\begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}\\{{a_{21}}}&{{a_{22}}}\end{array}} \right)\)     matriz 2×2 (2 filas y 2 columnas)

\(A = \left( {\begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\{{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\{{a_{31}}}&{{a_{32}}}&{{a_{33}}}\end{array}} \right)\)     matriz 3×3 (3 filas y 3 columnas)

A cada matriz cuadrada puede asignársele un número real que llamaremos su determinante y designaremos como \(det\left( A \right)\) o \(\left| A \right|\) . Para matrices \(2×2\) y \(3×3\) el determinante se calcula como sigue:

\[A = \left( {\begin{array}{*{20}{c}}{{\color{red}{a_{11}}}}&{{\color{fuchsia}{a_{12}}}}\\{{\color{fuchsia}{a_{21}}}}&{{\color{red}{a_{22}}}}\end{array}} \right)\; \Rightarrow \;\left| A \right| = {\color{red}{a_{11}}}.{\color{red}{a_{22}}} – {\color{fuchsia}{a_{12}}}.{\color{fuchsia}{a_{21}}}\]

\[A = \left( {\begin{array}{*{20}{c}}{{\color{lime}{a_{11}}}}&{{\color{blue}{a_{12}}}}&{{\color{red}{a_{13}}}}\\{{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\{{a_{31}}}&{{a_{32}}}&{{a_{33}}}\end{array}} \right) \Rightarrow \;\left| A \right| = {\color{lime}{a_{11}}}.\left| {\begin{array}{*{20}{c}}{{a_{22}}}&{{a_{23}}}\\{{a_{32}}}&{{a_{33}}}\end{array}} \right| – {\color{blue}{a_{12}}}.\left| {\begin{array}{*{20}{c}}{{a_{21}}}&{{a_{23}}}\\{{a_{31}}}&{{a_{33}}}\end{array}} \right| + {\color{red}{a_{13}}}.\left| {\begin{array}{*{20}{c}}{{a_{21}}}&{{a_{22}}}\\{{a_{31}}}&{{a_{32}}}\end{array}} \right|\]

Podemos expresar la fórmula \(\left[ 1 \right]\) utilizando determinantes como sigue:

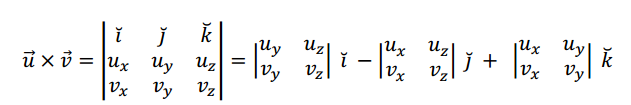
Con la notación habitual de ternas, resulta:

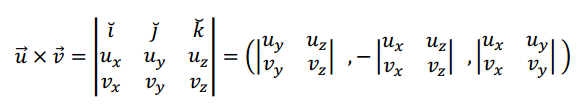
Veamos cómo utilizar esta regla práctica para calcular un producto vectorial:

\[\vec u = \left( {1,2,3} \right)\]

\[\vec v = \left( {0,2,5} \right)\]

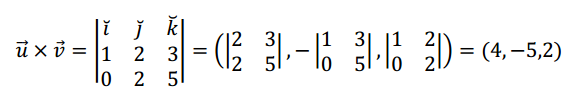
Comprobemos que el vector obtenido es ortogonal a \(\vec u\) y a \(\vec v\):

\[\left( {4, – 5,2} \right).\left( {1,2,3} \right) = 0\]

\[\left( {4, – 5,2} \right).\left( {0,2,5} \right) = 0\]

Interpretación geométrica del módulo del producto vectorial

Consideremos los siguientes vectores y calculemos el módulo del producto vectorial.

\[\vec u = \left( {1,2,3} \right)\;\;,\;\;\;\vec v = \left( {0,2,5} \right)\]

\[\vec u \times \vec v = \left( {4, – 5,2} \right)\]

\[\lVert \vec u \times \vec v \rVert = \sqrt {45} = 3.\sqrt 5 \]

¿Qué representa este número \(3\sqrt 5 \)?

Dibujemos cualquier par de vectores \(\vec u\) y \(\vec v\) y hagamos el paralelogramo determinado entre ellos:

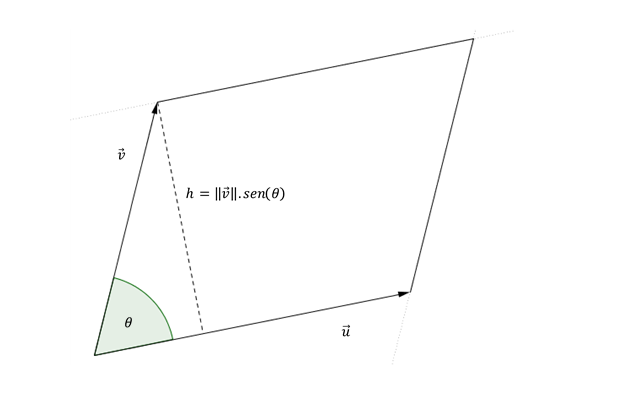
\[Área\;del\;paralelogramo = \lVert \vec u \rVert.h\]

\[sen\left( \theta \right) = \frac{h}{{\lVert \vec v \rVert}}\; \Rightarrow h = \lVert \vec v \rVert sen\left( \theta \right)\]

Conclusión: Dados dos vectores no paralelos, el módulo de su producto vectorial representa el área del paralelogramo determinado por dichos vectores.

Ejemplo

Dados \(A\left( {1,3,1} \right)\), \(B\left( {2, – 3,5} \right)\) y \(C\left( {0,2,1} \right)\) calcular el área del \({\rm{\Delta }}ABC\).

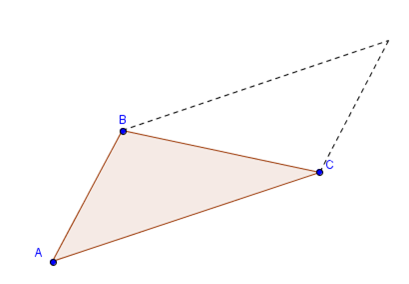
Podemos pensar al área del triángulo como la mitad del área del paralelogramo:

\[Área\;del\;triá ngulo = \frac{1}{2}. \lVert \overrightarrow {AB} \times \overrightarrow {AC} \rVert \]

\[\overrightarrow {AB} = \left( {1, – 6,4} \right)\]

\[\overrightarrow {AC} = \left( { – 1, – 1,0} \right)\]

\[\overrightarrow {AB} \times \overrightarrow {AC} = \left( {4, – 4, – 7} \right)\]

\[\lVert \overrightarrow {AB} \times \overrightarrow {AC} \rVert = \sqrt {16 + 16 + 49} = \sqrt {81} = 9\]

\[Área\;del\;triá ngulo = \frac{1}{2}.9 = 4,5\]

Producto mixto

Definición

Dados tres vectores \(\vec u,\vec v,\vec w \in {\mathbb{R}^3}\), se denomina producto mixto al número real que se obtiene multiplicando \(\vec u.\left( {\vec v \times \vec w} \right)\).

Para obtener el producto mixto, se calcula primero el producto vectorial y luego el escalar.

Dejamos como ejercicio para el lector, demostrar que:

\[\vec u.\left( {\vec v \times \vec w} \right) = \left( {\vec u \times \vec v} \right).\vec w\]

Veamos un ejemplo:

\[\vec u = \left( {1,2,3} \right)\]

\[\vec v = \left( {0,2,5} \right)\]

\[\vec w = \left( {0,0,2} \right)\;\]

\[\vec u.\left( {\vec v \times \vec w} \right)\]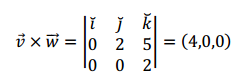

\[\vec u.\left( {\vec v \times \vec w} \right) = 4\]

Ahora hagamos al revés:

\[\left( {\vec u \times \vec v} \right).\vec w\]

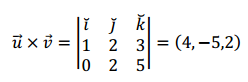
\[\left( {\vec u \times \vec v} \right).\vec w = \left( {4, – 5,2} \right).\left( {0,0,2} \right) = 4\]

Existe otro procedimiento para calcular el producto mixto a través de un determinante de 3×3.

Dados \(\vec u = \;\left( {{u_1},\;{u_2},\;{u_3}} \right),\;\;\vec v\; = \;\left( {{v_1},\;{v_2},\;{v_3}} \right)\;,\;\vec w\; = \;\left( {{w_1},\;{w_2},\;{w_3}} \right),\) el producto mixto es:

\[\vec u.\left( {\vec v \times \vec w} \right) = \left( {\vec u \times \vec v} \right).\vec w = \left| {\begin{array}{*{20}{c}}{{u_1}}&{{u_2}}&{{u_3}}\\{{v_1}}&{{v_2}}&{{v_3}}\\{{w_1}}&{{w_2}}&{{w_3}}\end{array}} \right| = {u_1}.\left| {\begin{array}{*{20}{c}}{{v_2}}&{{v_3}}\\{{w_2}}&{{w_3}}\end{array}} \right| – {u_2}.\left| {\begin{array}{*{20}{c}}{{v_1}}&{{v_3}}\\{{w_1}}&{{w_3}}\end{array}} \right| + {u_3}.\left| {\begin{array}{*{20}{c}}{{v_1}}&{{v_2}}\\{{w_1}}&{{w_2}}\end{array}} \right|\]

Calculemos con este método el producto mixto de: \(\vec u = \left( {1,2,3} \right)\)

\[\vec v = \left( {0,2,5} \right)\]

\[\vec w = \left( {0,0,2} \right)\;\]

\[\vec u.\left( {\vec v \times \vec w} \right) = \left| {\begin{array}{*{20}{c}}1&2&3\\0&2&5\\0&0&2\end{array}} \right| = 1.\left| {\begin{array}{*{20}{c}}2&5\\0&2\end{array}} \right| – 2.\left| {\begin{array}{*{20}{c}}0&5\\0&2\end{array}} \right| + 3.\left| {\begin{array}{*{20}{c}}0&2\\0&0\end{array}} \right| = 4\]

¿Qué significado tiene para la Geometría este número que hemos obtenido con el producto mixto?

Interpretación geométrica del producto mixto

Consideremos 3 vectores de \({\mathbb{R}^3}\) y construyamos un paralelepípedo (cuerpo cuyas seis caras son paralelogramos):

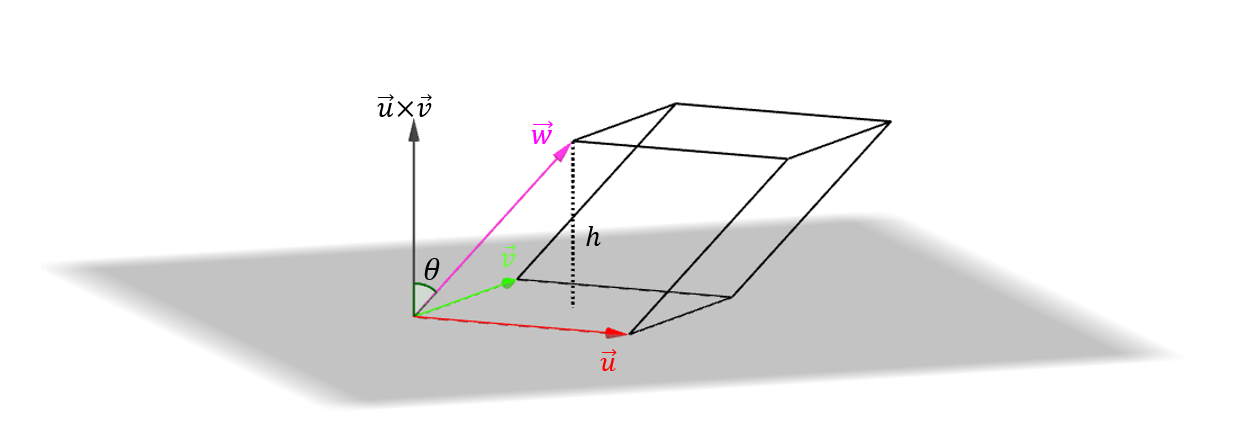
\[Volumen\;del\;paralelepípedo = área\;de\;la\;base\;.\;Altura\]

\[A = \lVert \vec u \times \vec v \rVert \]

\[h = \left| {\cos \left( \theta \right)} \right|\;\lVert \vec w\rVert \]

siendo \(\theta \) el ángulo entre \((\vec u \times \overrightarrow {v)} \;\;y\;\;\vec w\).

Observación: \(\cos \left( \theta \right)\) podría ser negativo, por eso tomamos su valor absoluto para el cálculo de la altura.

Entonces:

\[V = \lVert \vec u \times \vec v\ \rVert \; \lVert \vec w \rVert \;\left| {\cos \left( \theta \right)} \right|\;\;\;\;\;\;\left[ 1 \right]\]

Por otra parte:

\[\left( {\vec u \times \vec v} \right).\vec w = \lVert \vec u \times \vec v \rVert \; \lVert \vec w \rVert \;\cos \left( {á ng\left( {\vec u \times \vec v\;,\;\vec w} \right)} \right) = \lVert \vec u \times \vec v \rVert\;\lVert \vec w \rVert \;\cos \left( \theta \right)\;\;\;\;\left[ 2 \right]\]

De [1] y [2] resulta:

Retomemos el ejemplo con los vectores \(\vec u = \left( {1,2,3} \right),\) \(\vec v = \left( {0,2,5} \right),\) \(\vec w = \left( {0,0,2} \right)\)

De acuerdo al valor del producto mixto obtenido, el volumen del paralelepípedo determinado por los tres vectores es igual a 4.

Coplanaridad

Consideremos los vectores \(\vec u = \left( {1,0,3} \right),\) \(\vec v = \left( {0,0,2} \right),\) \(\vec w = \left( {3,0,4} \right)\). Les proponemos que verifiquen que el producto mixto da cero.

Si el producto mixto es cero, el volumen es 0, o sea que no se forma el paralelepípedo.

Veamos una gráfica de estos tres vectores:

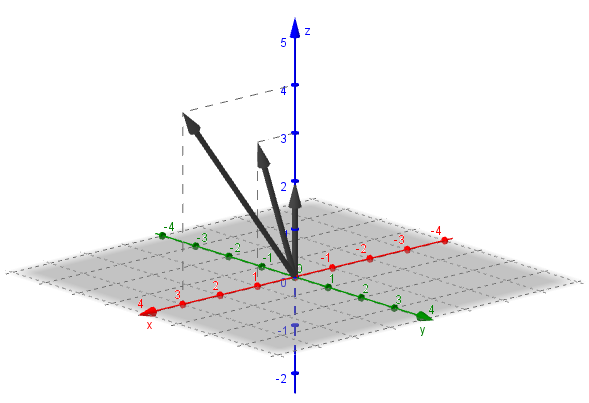
Observamos que los tres vectores están en el plano \(y = 0\), es decir que son coplanares.

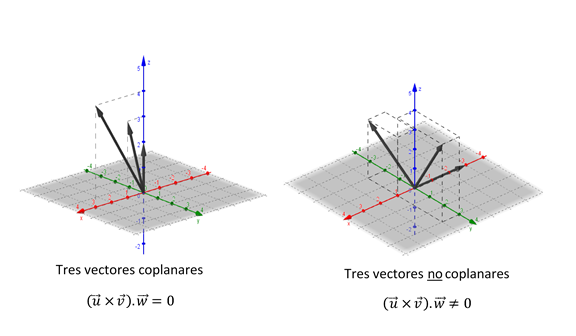
Tres vectores \(\vec u\), \(\vec v\), \(\vec w\) de \({\mathbb{R}^3}\) se denominan coplanares si considerados con un origen común, sus direcciones quedan incluidas en un mismo plano.

El producto mixto nos permite enunciar una condición de coplanaridad:

Lo que hemos desarrollado hasta aquí sobre vectores resulta una herramienta potente para el estudio de la geometría de rectas y planos en \({\mathbb{R}^3}\), como veremos a continuación.