Segundo Parcial Resuelto de AGA [23-06-2018]

Enunciado del primer parcial de álgebra [23-06-2018]

 

Ejercicio 1 – Autovalores y autovectores

Determine el valor de verdad de:

a) Si los autovalores de \(A \in {\mathbb{R}^{3 \times 3}}\) son \({\lambda _1}\) (doble) y \({\lambda _2}\) (simple) y el subespacio propio correspondiente a \({\lambda _1}\) tiene por ecuación \(2{x_1} – {x_3} = 0\), entonces \(A\) es diagonalizable.

b) Si A es una matriz cuadrada inversible entonces \(\lambda = 0\) es autovalor de A.

Resolución del ejercicio 1

Ítem a

Verdadero.

La ecuación \(2{x_1} – {x_3} = 0\) en \({\mathbb{R}^3}\) define un subespacio de dimensión 2. Que es el subespacio asociado al autovalor doble.

\[{m_{{\lambda _1}}} = 2\;\;\;\; \wedge \;\;\;\dim \left( {{S_{{\lambda _1}}}} \right) = 2\]

El autovalor simple tendrá un autoespacio asociado de dimensión 1 (porque la dimensión puede ser a lo sumo tan alta cómo la multiplicidad algebraica: \(1 \le \dim \left( {{S_\lambda }} \right) \le {m_\lambda }\)).

\[{m_{{\lambda _2}}} = 1\;\;\;\; \wedge \;\;\;\dim \left( {{S_{{\lambda _2}}}} \right) = 1\]

Además una propiedad establece que autovalores distintos están asociados a autovectores LI.

Así que obtendremos tres autovectores LI:

• Dos asociados a \({\lambda _1}\), y
• Uno asociado a \({\lambda _2}\)

Cómo existen tres autovectores LI, existe \(P\) y la matriz \(A\) es diagonalizable.

Ítem b

Falso.

Si \(A\) es inversible su determinante es diferente de cero:

A es inversible \( \Leftrightarrow \) \(\det \left( A \right) \ne 0\)

Pero para que \(\lambda  = 0\) sea autovalor debe cumplir con la definición de autovalor:

\(\lambda \) es autovalor de \(A\) \( \Leftrightarrow \) \(\det \left( {A – \lambda I} \right) = 0\)

Es decir:

\(\lambda  = 0\) es autovalor de \(A\) \( \Leftrightarrow \) \(\det \left( {A – 0.I} \right) = \det \left( A \right) = 0\)

Entonces no puede ser \(A\) inversible y \(\lambda  = 0\) autovalor poque debería ser \(\det \left( A \right) \ne 0\) y también \(\det \left( A \right) = 0\).

La afirmación es falsa.

Ejercicio 2 – Transformaciones lineales

Dada la transformación lineal \(F:{\mathbb{R}^2} \to {\mathbb{R}^2}\) \(F\left( {x,y} \right) = \left( {x – y, – x – 2y} \right)\).

a) ¿Es F inyectiva, sobreyectiva, biyectiva? Justificar

b) Hallar la matriz asociada a \(F\) respecto de la base canónica de \({\mathbb{R}^2}\) y, si existe, la expresión analítica de la transformación lineal \({F^{ – 1}}:{\mathbb{R}^2} \to {\mathbb{R}^2}\).

Resolución del ejercicio 2

Ítem a

Debemos decidir si:

• ¿Es inyectiva o no F?
• ¿Es sobreyectiva o no F?
• ¿Es biyectiva o no F?

Hay muchas formas de hacer esto.

Un teorema que puede ayudarnos es aquel que dice que si una TL  \(F:V \to W\) con \(\dim \left( V \right) = \dim \left( W \right)\) entonces:

\[F\;es\;inyectiva \Leftrightarrow F\;es\;sobreyectiva \Leftrightarrow F\;es\;biyectiva\]

Es decir que con determinar una sola de estas tres preguntas, sabemos la respuesta de las restantes.

Podemos usar el teorema porque \(F:{\mathbb{R}^2} \to {\mathbb{R}^2}\) (coinciden dimensiones de dominio y codominio).

Así que determinaremos si es inyectiva buscando el núcleo.

\[\left( {x,y} \right) \in Nu\left( F \right) \Leftrightarrow F\left( {x,y} \right) = \left( {0,0} \right)\]

\[ \Rightarrow \left( {x – y, – x – 2y} \right) = \left( {0,0} \right)\]

\[\left\{ {\begin{array}{*{20}{c}}{x – y = 0}\\{ – x – 2y = 0}\end{array}} \right. \Rightarrow \;\left\{ {\begin{array}{*{20}{c}}{x = 0}\\{y = 0}\end{array}} \right.\]

\[Nu\left( F \right) = \left\{ {\left( {0,0} \right)} \right\}\]

Así que F es inyectiva. Y también sobreyectiva y también biyectiva.

Veamos otra forma de pensarlo apenas distinta. Se puede expresar matricialmente el sistema:

\[\left( {\begin{array}{*{20}{c}}1&{ – 1}\\{ – 1}&{ – 2}\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\0\end{array}} \right)\]

Dónde la matriz de coeficientes es la matriz estándar de \(F\):

\[M\left( F \right) = \left( {\begin{array}{*{20}{c}}1&{ – 1}\\{ – 1}&{ – 2}\end{array}} \right)\]

Calculemos el determinante:

\[\det \left( {M\left( F \right)} \right) =  – 2 – \left( 1 \right) =  – 3\]

Cómo el determinante no es nulo, el sistema es SCD, es decir que la única solución es la trivial \(\left( {0,0} \right)\). Es decir que F es inyectiva.

Como F va de \({\mathbb{R}^2}\) a \({\mathbb{R}^2}\) es sobreyectiva y biyectiva también por la propiedad que mencionamos.

Si uno no se da cuenta de usar esta propiedad, puede probar que sobreyectiva. Para eso transformemos una base del dominio:

\[F\left( {1,0} \right) = \left( {1, – 1} \right)\]

\[F\left( {0,1} \right) = \left( { – 1, – 2} \right)\]

Entonces la imagen está generada por:

\[Im\left( F \right) = gen\left\{ {\left( {1, – 1} \right),\left( { – 1, – 2} \right)} \right\}\]

Cómo son a simple vista LI, la dimensión de la imagen es 2, y la TL es sobreyectiva.

Al ser inyectiva y sobreyectiva es también biyectiva.

Ítem b

Ya conocemos la matriz asociada en las bases canónicas:

\[M\left( F \right) = \left( {\begin{array}{*{20}{c}}1&{ – 1}\\{ – 1}&{ – 2}\end{array}} \right)\]

\[\det \left( {M\left( F \right)} \right) =  – 3\]

Para obtener la fórmula de \({F^{ – 1}}\) podemos aprovechar que:

\[{\left[ {M\left( F \right)} \right]^{ – 1}} = M\left( {{F^{ – 1}}} \right)\]

Recordemos que la inversa de \(A = \left( {\begin{array}{*{20}{c}}a&b\\c&d\end{array}} \right)\) es \({A^{ – 1}} = \frac{1}{{\det \left( A \right)}}.\left( {\begin{array}{*{20}{c}}d&{ – b}\\{ – c}&a\end{array}} \right)\):

\[{\left[ {M\left( F \right)} \right]^{ – 1}} = M\left( {{F^{ – 1}}} \right) = \frac{1}{{ – 3}}.\left( {\begin{array}{*{20}{c}}{ – 2}&1\\1&1\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{\frac{2}{3}}&{ – \frac{1}{3}}\\{ – \frac{1}{3}}&{ – \frac{1}{3}}\end{array}} \right)\]

Verifiquemos que calculamos bien la inversa haciendo el producto de \(M\left( F \right)\) con su inversa:

\[\left( {\begin{array}{*{20}{c}}1&{ – 1}\\{ – 1}&{ – 2}\end{array}} \right)\left( {\begin{array}{*{20}{c}}{\frac{2}{3}}&{ – \frac{1}{3}}\\{ – \frac{1}{3}}&{ – \frac{1}{3}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}1&0\\0&1\end{array}} \right)\]

Entonces haciendo el producto de \(M\left( {{F^{ – 1}}} \right)\) por un vector genérico obtenemos en que se transforma cada \(\left( {x,y} \right)\) al aplicar \({F^{ – 1}}\):

\[\left( {\begin{array}{*{20}{c}}{\frac{2}{3}}&{ – \frac{1}{3}}\\{ – \frac{1}{3}}&{ – \frac{1}{3}}\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{\frac{2}{3}x – \frac{1}{3}y}\\{ – \frac{1}{3}x – \frac{1}{3}y}\end{array}} \right)\]

Luego:

\[{F^{ – 1}}\left( {x,y} \right) = \left( {\frac{2}{3}x – \frac{1}{3}y, – \frac{1}{3}x – \frac{1}{3}y} \right)\]

 

Ejercicio 3 – Transformaciones lineales

Sean \(T:{\mathbb{R}^3} \to {\mathbb{R}^2}\) | \({M_{BB’}}\left( T \right) = \left( {\begin{array}{*{20}{c}}{ – 1}&1&1\\0&2&0\end{array}} \right)\) y las bases \(B = \left\{ {\left( { – 1,2,0} \right),\left( {1,0,1} \right),\left( {0,1,0} \right)} \right\}\) y \(B’ = \left\{ {\left( { – 1,1} \right),\left( {2, – 1} \right)} \right\}\). Encuentre \(h \in \mathbb{R}\) tal que \(\left( {1,2h + 1,0} \right) \in Nu\left( T \right)\)

Resolución del ejercicio 3

Conocemos la matriz \({M_{BB’}}\left( T \right)\) que opera con las coordenadas en \(B\) de los vectores del dominio.

Los vectores del núcleo deben cumplir que:

\[\left( {x,y,z} \right) \in Nu\left( T \right) \Leftrightarrow T\left( {x,y,z} \right) = \left( {0,0} \right)\]

Pero la matriz \({M_{BB’}}\left( T \right)\) no se multiplica por los vectores sino por sus coordenadas en base B.

Así que podemos denotar \(\left( {\begin{array}{*{20}{c}}a\\b\\c\end{array}} \right)\) a las coordenadas de los vectores del núcleo en base B, y escribir:

\[\left( {\begin{array}{*{20}{c}}{ – 1}&1&1\\0&2&0\end{array}} \right)\left( {\begin{array}{*{20}{c}}a\\b\\c\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\0\end{array}} \right)\]

Ahora podemos averiguar esas coordenadas:

\[ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{ – a + b + c = 0}\\{2b = 0}\end{array}} \right.\]

\[ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{a = c}\\{b = 0}\end{array}} \right.\]

\[\;\left( {x,y,z} \right) \in Nu \Rightarrow \;{\left[ {\left( {x,y,z} \right)} \right]_B} = \left( {\begin{array}{*{20}{c}}a\\0\\a\end{array}} \right)\]

\[\left( {x,y,z} \right) = a.\left( { – 1,2,0} \right) + 0.\left( {1,0,1} \right) + a.\left( {0,1,0} \right)\]

\[\left( {x,y,z} \right) = \left( { – a,2a,0} \right) + \left( {0,a,0} \right)\]

\[\left( {x,y,z} \right) = \left( { – a,3a,0} \right)\;\;\;,\;\;\;a \in \mathbb{R}\]

Por otra parte, el vector \(\left( {1,2h + 1,0} \right) \in Nu\).

Entonces para algún \(a \in \mathbb{R}\) debe ser:

\[\left( {1,2h + 1,0} \right) = \left( { – a,3a,0} \right)\]

\[ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{1 =  – a}\\{2h + 1 = 3a}\\{0 = 0}\end{array}} \right.\;\]

\[ \Rightarrow \;\;\left\{ {\begin{array}{*{20}{c}}{a =  – 1}\\{h =  – 2}\end{array}} \right.\]

Es decir que debe ser \(h =  – 2\).

Sería recomendable verificar que para \(h =  – 2\) efectivamente \(\left( {1,2h + 1,0} \right) \in Nu\).

 

Ejercicio 4 – Superficies

Sea la superficie \(S:A{\left( {x – 2} \right)^2} + B{\left( {y + 1} \right)^2} + C.{z^2} = 1\)

a) Halle \(A,\;B,\;C\) reales tal que la intersección de \(S\) con el plano \(x = 2\) sea la curva

\[3{y^2} – {z^2} + 6y + 2 = 0\]

y la intersección de S con el plano \(y =  – 1\) sea la curva

\[\frac{{{{\left( {x – 2} \right)}^2}}}{2} – 2{z^2} = 2\]

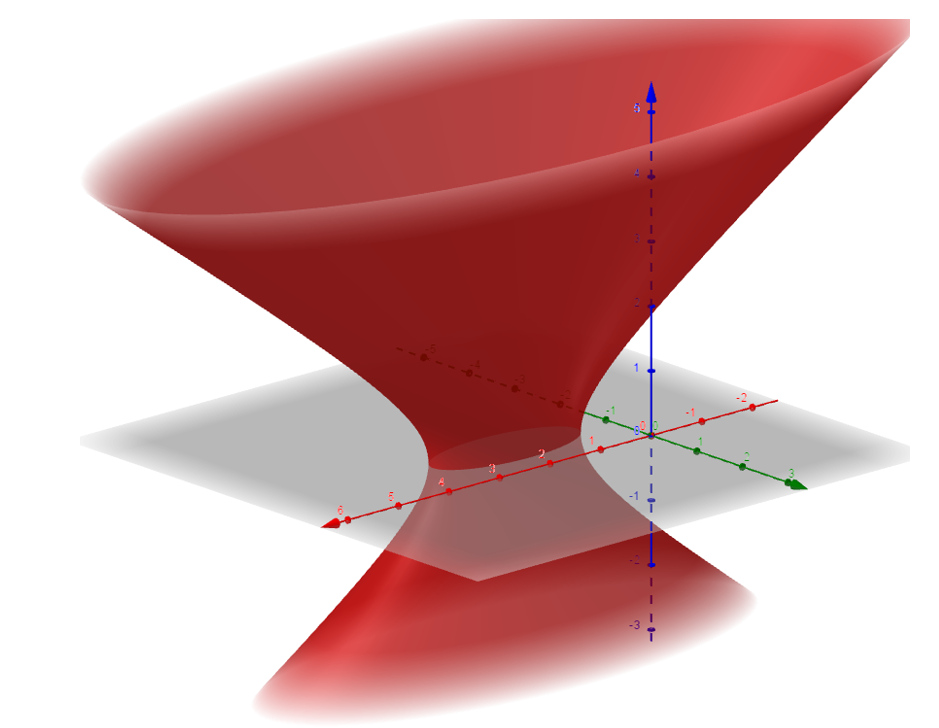
b) Grafique e identifique la superficie, para \(A = \frac{1}{4}\), \(B = 3\) y \(C = – 1\)

Resolución del ejercicio 4

Ítem a

En este tipo de ejercicios, hay que plantear las intersecciones a las que refiere el enunciado y comparar la ecuación que obtenemos con la que nos dan:

Intersección con \(x = 2\):

\[A{\left( {2 – 2} \right)^2} + B{\left( {y + 1} \right)^2} + C.{z^2} = 1\]

\[B{\left( {y + 1} \right)^2} + C.{z^2} = 1\]

\[B.{y^2} + 2y.B + B + C.{z^2} = 1\]

\[B.{y^2} + 2y.B + C.{z^2} + \left( {B – 1} \right) = 0\]

Comparamos esta expresión con la dada:

\[3{y^2} – {z^2} + 6y + 2 = 0\]

Cómo deben ser iguales, igualamos los coeficientes de cada término correspondiente (pintamos a los términos correspondientes del mismo color):

\[\left\{ {\begin{array}{*{20}{c}}{B = 3}\\{2B = 6}\\{C =  – 1}\\{B – 1 = 2}\end{array}} \right.\; \Rightarrow \;\;\left\{ {\begin{array}{*{20}{c}}{B = 3}\\{C =  – 1}\end{array}} \right.\]

Entonces ya averiguamos los valores de \(B = 3\) y \(C =  – 1\).

Ahora planteamos intersección con \(y =  – 1\) (usando que \(B = 3\) y \(C =  – 1\)) y hacemos lo mismo:

\[A{\left( {x – 2} \right)^2} + 3.{\left( { – 1 + 1} \right)^2} – 1.{z^2} = 1\]

\[A{\left( {x – 2} \right)^2} + 3.{\left( { – 1 + 1} \right)^2} – 1.{z^2} = 1\]

\[A{\left( {x – 2} \right)^2} – 1.{z^2} = 1\]

\[A{\left( {x – 2} \right)^2} – 1.{z^2} = 1\;\;\;\;\;\;\left( {ECUACIÓN\# 1} \right)\]

Comparamos esta expresión con la dada:

\[\frac{{{{\left( {x – 2} \right)}^2}}}{2} – 2{z^2} = 2\]

Para tener el mismo número en el miembro derecho podemos multiplicar por dos a  \(\left( {ECUACIÓN\# 1} \right)\):

\[2A{\left( {x – 2} \right)^2} – 2{z^2} = 2\;\;\;\;\left( {ECUACIÓN\# 1′} \right)\]

Ahora sí comparamos coeficientes:

\[2A = \frac{1}{2} \Rightarrow A = \frac{1}{4}\]

Concluyendo llegamos a que:

\[B = 3\]

\[C =  – 1\]

\[A = \frac{1}{4}\]

Ítem b

En este caso debemos reemplazar por para \(A = \frac{1}{4}\), \(B = 3\) y \(C =  – 1\) en la expresión:

\[A{\left( {x – 2} \right)^2} + B{\left( {y + 1} \right)^2} + C.{z^2} = 1\]

Queda:

\[\frac{1}{4}{\left( {x – 2} \right)^2} + 3{\left( {y + 1} \right)^2} – 1{z^2} = 1\]

Las intersecciones con planos paralelos a los coordenados que pasen por en centro \(\left( {2, – 1,0} \right)\) son:

• Hipérbola (intersección con \(x = 2\))
• Hipérbola (intersección con \(y = – 1\))
• Elipse (intersección con \(z = 0\))

Así que se trata de un hiperboloide (porque dos intersecciones son hipérbolas).

De una hoja (porque la tercera intersección es una elipse).

Es un hiperboloide de una hoja con eje paralelo al \(z\), con centro en \(\left( {2, – 1,0} \right)\)

Ejercicio 5 – Números complejos

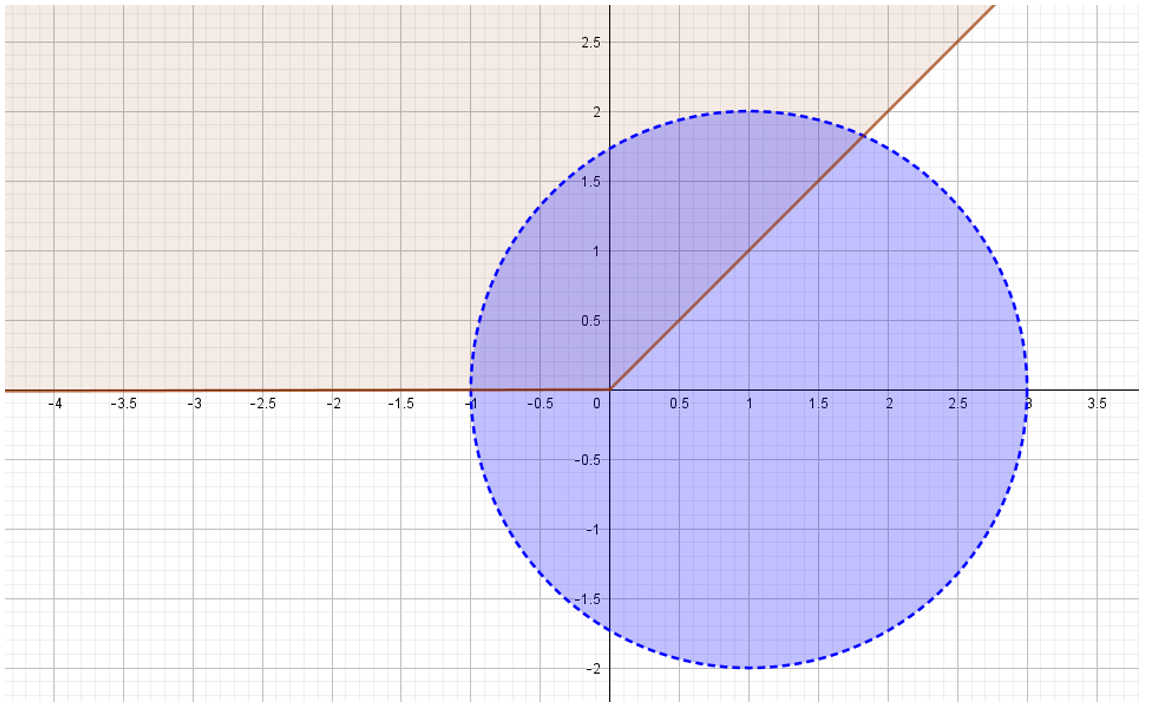
Hallar y graficar en el plano complejo la región:

\(R = \left\{ {z \in \mathbb{C}\;|\;\;\left| {z – 1} \right| < 2\; \wedge \frac{\pi }{4} \le \arg \left( z \right) \le \pi } \right\}\)

Resolución del ejercicio 5

\[R = \left\{ {z \in \mathbb{C}\;|\;\;\left| {z – 1} \right| < 2\; \wedge \frac{\pi }{4} \le \arg \left( z \right) \le \pi } \right\}\]

\[z = x + i.y\]

\[\left| {z – 1} \right| < 2\]

\[\left| {x + i.y – 1} \right| < 2\]

\[\left| {x – 1 + i.y} \right| < 2\]

\[\sqrt {{{\left( {x – 1} \right)}^2} + {y^2}}  < 2\]

Aplicando cuadrado a ambos miembros:

\[{\left( {x – 1} \right)^2} + {y^2} < 4\]

Interior del circulo centrado en \(\left( {1,0} \right)\) con radio 2 [no incluimos el borde].