El siguiente es el enunciado y resolución completa del primer parcial de álgebra y geometría analítica tomado el día 09-09-2017, en el curso semi-presencial.
Enunciado del primer parcial de álgebra [09-09-2017]

Ejercicio 1 – Haz de planos
Halle, si existe, el plano del haz \({\alpha _1}\left( {x – y – 2z + 5} \right) + {\alpha _2}\left( {2x + y – 3} \right) = 0\;\;\;\;{\alpha _1},{\alpha _2} \in \mathbb{R}\) que sea perpendicular a la recta \(r:\left( {x,y,z} \right) = \left( {1,0, – 2} \right) + \lambda \left( {4, – 1, – 4} \right)\). En caso de que exista, grafique dicho plano.
Resolución ejercicio 1
Aplicamos propiedad distributiva en la ecuación del haz de planos y luego sacamos factor común:
\[{\alpha _1}\left( {x – y – 2z + 5} \right) + {\alpha _2}\left( {2x + y – 3} \right) = 0\;\;\;\;{\alpha _1},{\alpha _2} \in \mathbb{R}\]
\[\left( {{\alpha _1} + 2{\alpha _2}} \right)x + \left( { – {\alpha _1} + {\alpha _2}} \right)y + \left( { – 2{\alpha _1}} \right)z + \left( {5{\alpha _1} – 3{\alpha _2}} \right) = 0\]
Los coeficientes de \(x\), \(y\) y \(z\) son las componentes de un vector normal del plano.
\[\vec n = \left( {{\alpha _1} + 2{\alpha _2}, – {\alpha _1} + {\alpha _2}, – 2{\alpha _1}} \right)\]
Hagamos un diagrama con un plano y una recta perpendicular a él:
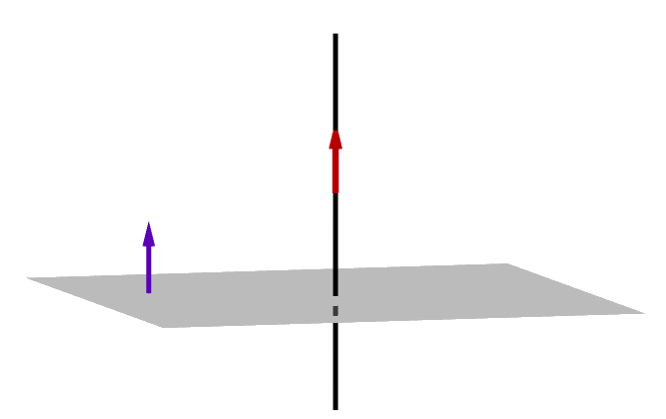
Cómo el diagrama nos ayuda ver, para que la recta sea perpendicular al plano, el vector director de la recta, debe ser paralelo al vector normal del plano.
Podemos entonces igualar al vector normal del plano con el vector director de la recta:
\[\left\{ {\begin{array}{*{20}{c}}{{\alpha _1} + 2{\alpha _2} = 4}\\{ – {\alpha _1} + {\alpha _2} = – 1}\\{ – 2{\alpha _1} = – 4}\end{array}} \right.\;\]
\[ \Rightarrow \;\;\left\{ {\begin{array}{*{20}{c}}{2 + 2.1 = 4}\\{{\alpha _2} = 1}\\{{\alpha _1} = 2}\end{array}} \right.\]
Para que el vector normal del plano sea \(\left( {4, – 1, – 4} \right)\), debe ser \({\alpha _1} = 2\) y \({\alpha _2} = 1\).
Reemplazando \({\alpha _1} = 2\) y \({\alpha _2} = 1\) en la ecuación del haz obtenemos:
\[4x – y – 4z + 7 = 0\]
Observación:
Uno podría argumentar que no es válido igualar el vector normal del plano con el vector director de la recta. Porque no deben ser idénticos sino sólo paralelos. Es decir que uno debe ser proporcional al otro. Pero sí es válido igualarlo. Veamos por qué: en la ecuación del haz de planos para cada relación entre \({\alpha _1}\) y \({\alpha _2}\) se determina un único plano. Por ejemplo si se toma \({\alpha _1} = 5{\alpha _2}\) se determina un único plano independientemente de si \({\alpha _1} = 5\) y \({\alpha _2} = 1\) o si \({\alpha _1} = 10\) y \({\alpha _2} = 2\).
Verifiquemos esto en el caso del ejercicio. Si en lugar de igualarlo a \(\left( {4, – 1, – 4} \right)\) lo hacíamos con \(\left( {8, – 2, – 8} \right)\) (un vector paralelo) obteníamos también unos valores posibles de \({\alpha _2}\) y \({\alpha _1}\) que nos llevaban a otra ecuación posible para el mismo plano:
\[\left\{ {\begin{array}{*{20}{c}}{{\alpha _1} + 2{\alpha _2} = 8}\\{ – {\alpha _1} + {\alpha _2} = – 2}\\{ – 2{\alpha _1} = – 8}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{4 + 2.2 = 8}\\{{\alpha _2} = 2}\\{{\alpha _1} = 4}\end{array}} \right.\]
\[\pi :8x – 2y – 8z + 14 = 0\]
Dividiendo por dos a ambos miembros vemos que se trata del mismo plano:
\[4x – y – 4z + 7 = 0\]
En general si lo igualamos a un vector paralelo a \(\left( {4, – 1, – 4} \right)\) vemos que se encuentra una relación entre \({\alpha _1}\) y \({\alpha _2}\). Esta resolución es un poquito más larga:
\[\left\{ {\begin{array}{*{20}{c}}{{\alpha _1} + 2{\alpha _2} = 4k}\\{ – {\alpha _1} + {\alpha _2} = – k}\\{ – 2{\alpha _1} = – 4k}\end{array}} \right.\]
\[ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{\alpha _1} + 2{\alpha _2} – 4k = 0}\\{ – {\alpha _1} + {\alpha _2} + k = 0}\\{ – 2{\alpha _1} + 4k = 0}\end{array}} \right.\]
Planteamos la matriz de coeficientes y vamos escalonando con operaciones elementales de filas:
\[\left( {\begin{array}{*{20}{c}}1&2&{ – 4}\\{ – 1}&1&1\\{ – 2}&0&4\end{array}} \right)\]
\[\mathop \to \limits_{\begin{array}{*{20}{c}}{{F_2} + {F_1}}\\{{F_3} + 2{F_1}}\end{array}} \left( {\begin{array}{*{20}{c}}1&2&{ – 4}\\0&3&{ – 3}\\0&4&{ – 4}\end{array}} \right)\]
\[\mathop \to \limits_{\begin{array}{*{20}{c}}{\frac{1}{3}.{F_2}}\\{{F_3} – 4{F_2}}\end{array}} \left( {\begin{array}{*{20}{c}}1&2&{ – 4}\\0&1&{ – 1}\\0&0&0\end{array}} \right)\]
\[\mathop \to \limits_{{F_1} – 2{F_1}} \left( {\begin{array}{*{20}{c}}1&0&{ – 2}\\0&1&{ – 1}\\0&0&0\end{array}} \right)\]
Ahora que escalonamos la matriz de coeficientes volvemos a escribir el sistema de ecuaciones simplificado:
\[\left\{ {\begin{array}{*{20}{c}}{{\alpha _1} – 2k = 0}\\{{\alpha _2} – k = 0}\end{array}} \right.\]
\[ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{\alpha _1} = 2k}\\{{\alpha _2} = k}\end{array}} \right.\]
\[ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{\alpha _1} = 2{\alpha _2}}\\{k \in R}\end{array}} \right.\]
Obtuvimos que para que el plano sea paralelo a \(\left( {4, – 1, – 4} \right)\) debe ocurrir que \({\alpha _1} = 2{\alpha _2}\). Cualquier pareja de valores que cumpla esa relación está bien.
Cómo habíamos dicho antes: cada plano del haz de planos queda definido por una “relación entre \({\alpha _1}\) y \({\alpha _2}\)”. Podría ser en particular \({\alpha _2} = 1\) y \({\alpha _2} = 2\), o cómo en el segundo ejemplo \({\alpha _2} = 2\) y \({\alpha _2} = 4\)… en general es \({\alpha _1} = 2{\alpha _2}\).
Ejercicio 2 – Proyección de una recta sobre un plano
Sean la recta \(r:\left( {x,y,z} \right) = \left( {4, – 2,0} \right) + t\left( { – 4,4,1} \right)\) con \(t \in \mathbb{R}\) y el plano \(\beta : x – y – z = 0\). Obtenga la ecuación de la recta proyección de \(r\) sobre \(\beta \).
Resolución del ejercicio 2
Hagamos un diagrama general que contenga un plano, una recta y la proyección de la recta sobre el plano:
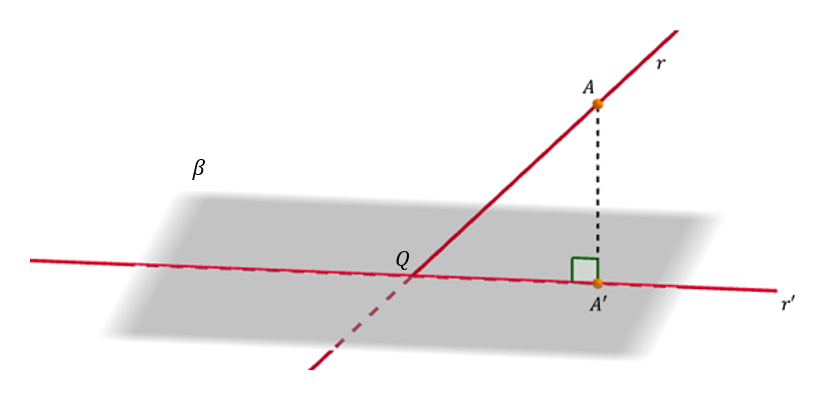
Este diagrama es para el caso de que \(r\) no sea paralela con el plano \(\beta \). Es nuestro caso: vemos que la recta y el plano no son paralelos. Porque el vector director de la recta \(\left( { – 4,4,1} \right)\) no es perpendicular al vector normal del plano \(\left( {1, – 1, – 1} \right)\).
La recta \(r’\) es aquella que pasa por \(Q\) (siendo \(\left\{ Q \right\} = r \cap \beta \)) y \(A’ = pro{y_\beta }\left( A \right)\).
Busquemos \(\left\{ Q \right\} = \beta \cap r\). Para eso planteamos las ecuaciones paramétricas de \(r\) y las reemplazamos en la ecuación del plano \(\beta \):
\[r:\left\{ {\begin{array}{*{20}{c}}{x = 4 – 4t}\\{y = – 2 + 4t}\\{z = t}\end{array}} \right.\;\;\;\;,\;\;t \in \mathbb{R}\]
\[\beta : x – y – z = 0\]
\[\left( {4 – 4t} \right) – \left( { – 2 + 4t} \right) – t = 0\]
\[ \Rightarrow 6 – 9t = 0\]
\[ \Rightarrow t = \frac{2}{3}\]
Ahora reemplazamos \(t = \frac{2}{3}\) en la ecuación de \(r\):
\[\left\{ Q \right\} = r \cap \beta = \left\{ {\left( {\frac{4}{3},\frac{2}{3},\frac{2}{3}} \right)} \right\}\]
Buscamos \(A’ = pro{y_\beta }\left( A \right)\). Para eso tomamos un punto de la recta, por ejemplo \(A = \left( {4, – 2,0} \right)\). Armamos la recta auxiliar \(t\) (perpendicular al plano y que pasa por \(A\)):
\[t:\left( {x,y,z} \right) = \left( {4, – 2,0} \right) + \lambda \left( {1, – 1, – 1} \right)\]
Buscamos la intersección \(t \cap \beta \):
\[t:\left\{ {\begin{array}{*{20}{c}}{x = 4 + \lambda }\\{y = – 2 – \lambda }\\{z = – \lambda }\end{array}} \right.\;\;,\;\;\;\lambda \in \mathbb{R}\]
\[\left( {4 + \lambda } \right) – \left( { – 2 – \lambda } \right) – \left( { – \lambda } \right) = 0\]
\[ \Rightarrow 6 + 3\lambda = 0\]
\[ \Rightarrow \lambda = – 2\]
\[A’ = \left( {2,0,2} \right)\]
Un vector director de \(r’\) puede ser:
\[\overrightarrow {A’Q} = \left( {\frac{4}{3},\frac{2}{3},\frac{2}{3}} \right) – \left( {2,0,2} \right) = \left( { – \frac{2}{3},\frac{2}{3}, – \frac{4}{3}} \right)\]
Finalmente escribimos la ecuación vectorial de la recta:
\[r’:\left( {x,y,z} \right) = \left( {2,0,2} \right) + \alpha \left( { – \frac{2}{3},\frac{2}{3}, – \frac{4}{3}} \right)\]
Ejercicio 3 – Determinante de una matriz
¿Verdadero o falso? Justifique su respuesta.
Si \(A \in {\mathbb{R}^{3 \times 3}}\; \wedge \;{A^2} = A\; \wedge \;A\) es inversible, entonces \(\left| {3A} \right| = 27\).
Resolución del ejercicio 3
Si \({A^2} = A\) entonces sus determinantes son iguales:
\[\det \left( {{A^2}} \right) = \det \left( A \right)\]
Por propiedades de determinantes:
\[ \Rightarrow {\left[ {\det \left( A \right)} \right]^2} = \det \left( A \right)\]
Cómo es inversible… \(\det \left( A \right) \ne 0\) entonces podemos dividir a ambos miembros por \({\rm{det}}\left( A \right)\):
\[ \Rightarrow \det \left( A \right) = 1\]
Ahora tomemos \(\det \left( {3A} \right)\) y apliquemos propiedades:
\[{\rm{\;}}\det \left( {3A} \right) = {3^3}.\det \left( A \right)\]
Cómo sabemos que \(\det \left( A \right) = 1\):
\[\det \left( {3A} \right) = 27.1 = 27\]
La afirmación es verdadera.
Ejercicio 4 – Coordenadas de un vector en una base
Sea \(B = \left\{ {{v_1} = \left( {1,1,1} \right),{v_2},{v_3}} \right\}\) una base de \({\mathbb{R}^3}\).
Si \(\vec u = \left( { – 1,1,2} \right)\) y \(\vec w = \left( {0,2, – 3} \right)\) son vectores de \({\mathbb{R}^3}\) tales que sus coordenadas en la base \(B\) son \({\left[ {\vec u} \right]_B} = \left( {\begin{array}{*{20}{c}}1\\{\begin{array}{*{20}{c}}{ – 2}\\3\end{array}}\end{array}} \right)\) y \({\left[ {\vec w} \right]_B} = \left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}2\\3\end{array}}\end{array}} \right)\) halle \(\overrightarrow {{v_2}} \) y \(\overrightarrow {{v_3}} \).
Resolución del ejercicio 4
El vector \(\left( { – 1,1,2} \right)\) tiene coordenadas \(\color{red}{1}\), \( \color{red}{-2}\), \(\color{red}{3}\) en la base \(B\), entonces:
\[\left( { – 1,1,2} \right) = \color{red}{1}.\left( {1,1,1} \right) \color{red}{-2}.{v_2} + \color{red}{3}.{v_3}\]
Pasamos \(\left( {1,1,1} \right)\) restando y obtenemos la ecuación 1:
\[\left( { – 2,0,1} \right) = – 2.{v_2} + 3.{v_3}\;\;\;\;\left[ 1 \right]\]
El vector \(\left( {0,2, – 3} \right)\) tiene coordenadas \(\color{fuchsia}{0}\),\(\color{fuchsia}{2}\), \(\color{fuchsia}{3}\) en la base \(B\):
\[\left( {0,2, – 3} \right) = \color{fuchsia}{0}.\left( {1,1,1} \right) + \color{fuchsia}{2}.{v_2} + \color{fuchsia}{3}.{v_3}\;\;\;\left[ 2 \right]\]
Podemos armar un sistema de ecuaciones con estas dos ecuaciones:
\[\left\{ {\begin{array}{*{20}{c}}{\left( { – 2,0,1} \right) = – 2.{v_2} + 3.{v_3}}\\{\left( {0,2, – 3} \right) = 2.{v_2} + 3.{v_3}}\end{array}} \right.\]
Ahora sumamos las ecuaciones para eliminar \({v_2}\) y poder despejar \({v_3}\):
\[\left( { – 2,2, – 2} \right) = 6.{v_3}\]
\[ \Rightarrow {v_3} = \left( { – \frac{1}{3},\frac{1}{3}, – \frac{1}{3}} \right)\]
Reemplazamos \({v_3} = \left( { – \frac{1}{3},\frac{1}{3}, – \frac{1}{3}} \right)\) en la segunda ecuación:
\[\left( {0,2, – 3} \right) = 2.{v_2} + \left( { – 1,1, – 1} \right)\]
\[\left( {0,2, – 3} \right) – \left( { – 1,1, – 1} \right) = 2.{v_2}\]
\[\left( {1,1, – 2} \right) = 2.{v_2}\]
\[{v_2} = \left( {\frac{1}{2},\frac{1}{2}, – 1} \right)\]
Ejercicio 5 – Subespacios vectoriales, intersección de subespacios, complemento ortogonal
Dados los subespacios de \({\mathbb{R}^3}\):
\[{S_1} = gen\left\{ {\left( {1,1,1} \right),\left( {0,1,1} \right)} \right\}\]
\[{S_2} = \left\{ {\left( {x,y,z} \right) \in {\mathbb{R}^3}\;|\;x – y = 0\; \wedge \;\;kx – z = 0} \right\}\]
a) Halle todos los valores de \(k \in \mathbb{R}\) para que la dimensíon de \({S_1} \cap {S_2}\) sea igual a cero.
b) Para \(k = 1\) halle \(S_2^ \bot \), una base y su dimensión.
Resolución del ejercicio 5
Ítem a
Forma 1 de pensarlo
\({S_1}\) es un plano (definido por sus vectores directores y que pasa por el origen), y \({S_2}\) es una recta (definida como intersección de dos planos).
Para que \(\dim \left( {{S_1} \cap {S_2}} \right) = 0\), la recta no tiene que ser paralela al plano.
\[\vec n = \left| {\begin{array}{*{20}{c}}i&j&k\\1&1&1\\0&1&1\end{array}} \right| = \left( {0, – 1,1} \right)\]
\[\vec v = \left| {\begin{array}{*{20}{c}}i&j&k\\1&{ – 1}&0\\k&0&{ – 1}\end{array}} \right| = \left( {1,1,k} \right)\]
\[\left( {0, – 1,1} \right)\left( {1,1,k} \right) = 0\]
\[ \Rightarrow – 1 + k = 0\]
\[ \Rightarrow k = 1\]
Si \(k = 1\) la recta es paralela al plano, y entonces la intersección no tiene dimensión 0.
Para todo \(k\) diferente de 1, \(\dim \left( {{S_1} \cap {S_2}} \right) = 0\).
Forma 2 de pensarlo
Hallemos las ecuaciones de \({S_1}\):
\[{S_1} = gen\left\{ {\left( {1,1,1} \right),\left( {0,1,1} \right)} \right\}\]
\[\left( {x,y,z} \right) = \alpha \left( {1,1,1} \right) + \beta \left( {0,1,1} \right)\]
\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{x = \alpha }\\{y = \alpha + \beta }\\{z = \alpha + \beta }\end{array}} \right. \Rightarrow \left\{ {y = z \wedge \;x \in \mathbb{R}} \right.\)
\[{S_1} = \left\{ {\left( {x,y,z} \right) \in {\mathbb{R}^3}\;|\;y – z = 0} \right\}\]
\({S_1} \cap {S_2}\) debe cumplir con las ecuaciones de \({S_1}\) y también con las de \({S_2}\):

Para que \(\dim \left( {{S_1} \cap {S_2}} \right) = 0\) la única solución de este sistema de tres ecuaciones debe ser la trivial: \(\left( {0,0,0} \right)\).
\[\left\{ {\begin{array}{*{20}{c}}{y – z = 0}\\{x – y = 0}\\{kx – z = 0}\end{array}} \right.\]
Para que un sistema lineal homogéneo tenga solución única el determinante de la matriz de coeficientes debe ser diferente de cero:
\[\left| {\begin{array}{*{20}{c}}0&1&{ – 1}\\1&{ – 1}&0\\k&0&{ – 1}\end{array}} \right| = – 1.\left| {\begin{array}{*{20}{c}}1&0\\k&{ – 1}\end{array}} \right| – 1.\left| {\begin{array}{*{20}{c}}1&{ – 1}\\k&0\end{array}} \right| = 1 – k \ne 0\]
Es decir que \(k \ne 1\) para que \(\dim \left( {{S_1} \cap {S_2}} \right) = 0\).
Ítem b
Reemplazamos \(k = 1\):
\[{S_2} = \left\{ {\left( {x,y,z} \right) \in {\mathbb{R}^3}\;|\;x – y = 0\; \wedge x – z = 0} \right\}\]
Entonces los vectores de \({S_2}\) son tales que \(x = y\) y \(x = z\):
\[\left( {x,x,x} \right) = x\left( {1,1,1} \right)\]
\[{B_{{S_2}}} = \left\{ {\left( {1,1,1} \right)} \right\}\]
Los vectores de \(S_2^ \bot \) son tales que en producto interno con los de \({S_2}\) dan 0:
\[\left( {1,1,1} \right).\left( {x,y,z} \right) = 0\]
\[ \Rightarrow x + y + z = 0\]
\[ \Rightarrow x = – y – z\]
\[ \Rightarrow \left( { – y – z,y,z} \right) = y.\left( { – 1,1,0} \right) + z.\left( { – 1,0,1} \right)\]
\[{B_{S_2^ \bot }} = \left\{ {\left( { – 1,1,0} \right),\left( { – 1,0,1} \right)} \right\}\;\;\;\]
\[ \Rightarrow \;\dim \left( {S_2^ \bot } \right) = 2\]

