Ecuaciones del plano

Deducción de la ecuación general del plano

Dada una dirección en \({\mathbb{R}^3}\), existen infinitos planos perpendiculares a la misma. Si conocemos además un punto del plano, éste queda determinado de forma única.

Nos proponemos hallar la ecuación del plano \(\pi \) que pasa por \({P_0}\left( {{x_0},{y_0},{z_0}} \right)\) y es perpendicular al vector \(\vec n = \left( {a,b,c} \right).\) El vector \(\vec n\) se denomina vector normal del plano.

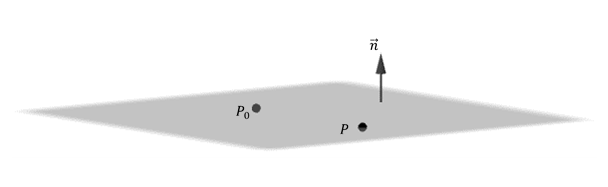
¿Qué condición debe cumplir un punto \(P\left( {x,y,z} \right)\) para estar en el plano \(\pi \)? Si armamos el vector \(\overrightarrow {\;{P_0}P} \;\), éste debe ser paralelo al plano, o sea perpendicular al vector normal del plano:

\[P\left( {x,y,z} \right) \in \pi \; \Leftrightarrow \overrightarrow {\;{P_0}P} \bot \vec n\;\; \Leftrightarrow \;\;\overrightarrow {{P_0}P} .\vec n = 0\]

\[\left( {x – {x_{0\;}},\;y – {y_0},\;z – {z_0}} \right).\left( {a,b,c} \right) = 0\]

\[a\left( {x – {x_0}} \right) + b\left( {y – {y_0}} \right) + c\left( {z – {z_0}} \right) = 0\]

Ejemplo

Hallar la ecuación del plano perpendicular al vector \(\vec n = \left( {3,2,1} \right)\) que pasa por el punto \({P_0}\left( {1,1, – 1} \right)\).

Las componentes de \(\vec n\) nos indican los coeficientes \(a\), \(b\) y \(c\) de la ecuación del plano:

\[\pi :\;\;3x + 2y + z + d = 0\]

¿Cómo hallamos \(d\)?

El punto debe verificar la ecuación, entonces reemplazamos \({P_0}\) y obtenemos el coeficiente que faltaba:

\[3.1 + 2.1 – 1 + d = 0\; \Rightarrow d = – 4\]

Así obtenemos la ecuación del plano:

\[\pi :\;\;3x + 2y + z – 4 = 0\]

Éste es el único plano que pasa por el punto \({P_0}\;\;\)y es perpendicular al vector \(\vec n\).

Para efectuar un gráfico aproximado del plano que obtuvimos, podemos buscar sus intersecciones con los ejes coordenados:

Para hallar la intersección con el eje \(x\), debemos plantear \(y = z = 0\) y despejar el valor de \(x\). Análogamente para las otras intersecciones, tal como se muestra en el siguiente cuadro:

 

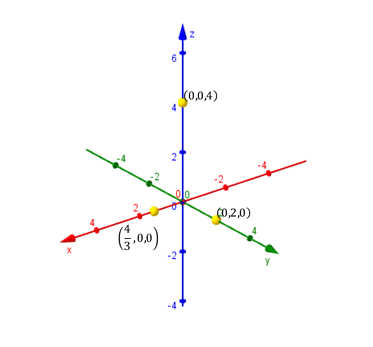
Tres puntos no alineados determinan un único plano que los contiene. Trazamos los segmentos que unen los puntos hallados y obtenemos la representación gráfica de una porción del plano:

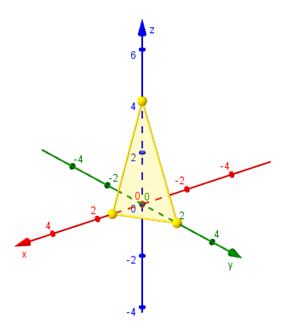
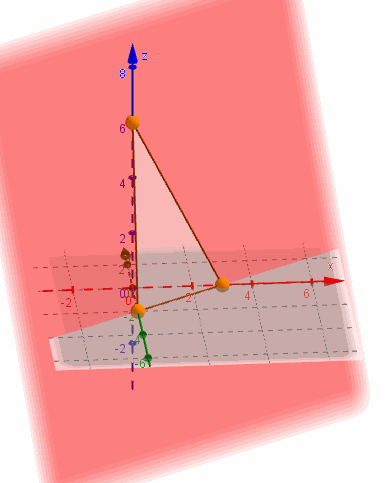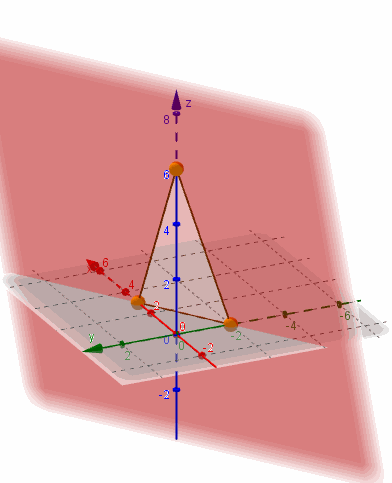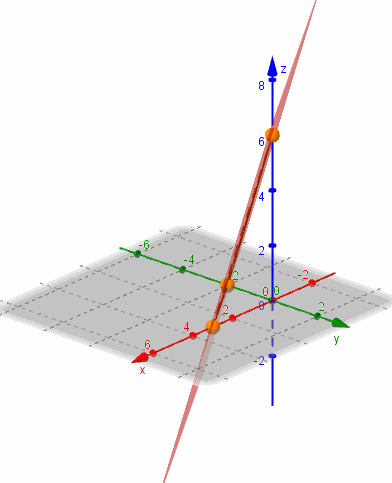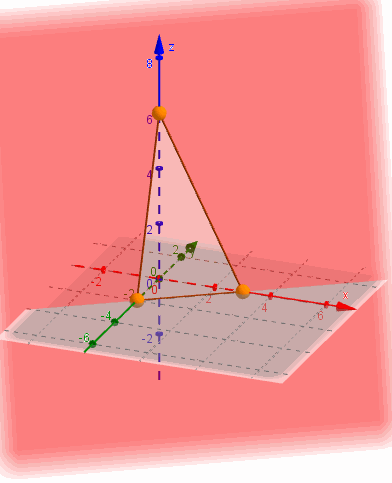
Mostramos una gráfica del plano realizada con GeoGebra:

 

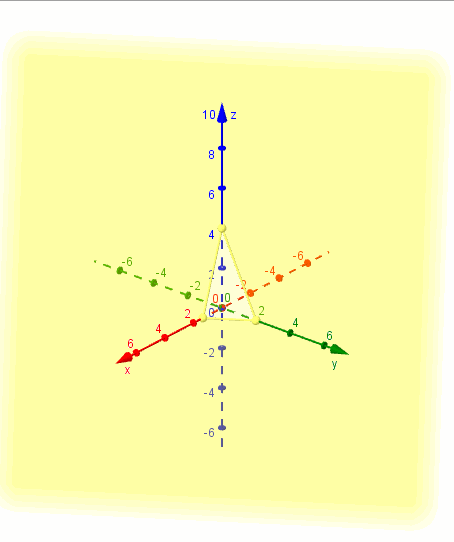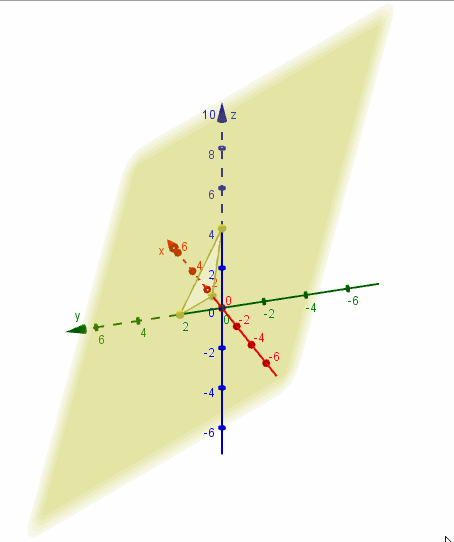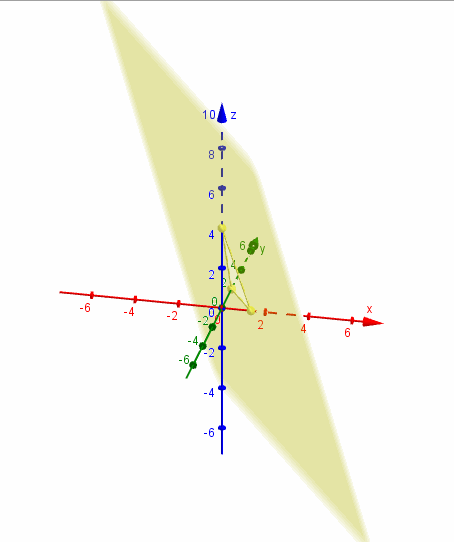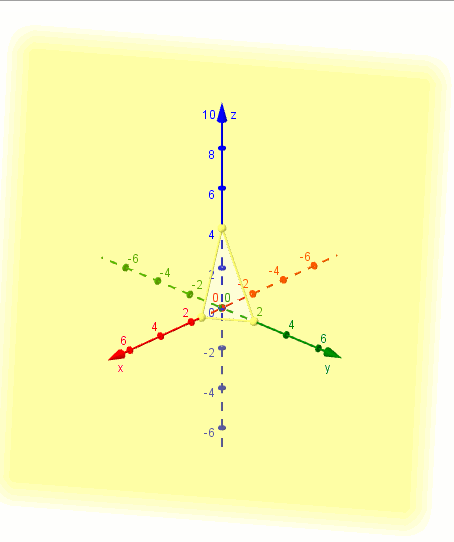
Ejemplo

Dados los puntos \(R\left( {1,2,3} \right)\) y \(S\left( {3, – 1,2} \right)\), encontrar la ecuación del plano que corta perpendicularmente al segmento \(RS\) en su punto medio.

Resolución

Busquemos las coordenadas del punto medio:

\[M = \left( {\frac{{1 + 3}}{2},\frac{{2 + \left( { – 1} \right)}}{2},\frac{{3 + 2}}{2}} \right) = \left( {2,\frac{1}{2},\frac{5}{2}} \right)\]

Como el plano corta perpendicularmente al segmento \(RS\), podemos tomar \(\overrightarrow {RS} \;\;\)como vector normal del plano:

\[\overrightarrow {RS} = \left( {2, – 3, – 1} \right)\]

Escribimos la ecuación del plano al que llamaremos \(\beta \):

\[\beta :\;\;\;2x – 3y – 1z + d = 0\]

Para hallar \(d\) reemplazamos el punto \(M\):

\[2.2 – 3.\frac{1}{2} – \frac{5}{2} + d = 0\; \Rightarrow d = 0\]

Y así obtenemos la ecuación buscada:

\[\beta :\;\;\;2x – 3y – z = 0\]

Este plano pasa por el origen, o sea que interseca a los tres ejes en \(\left( {0,0,0} \right)\). Necesitamos al menos dos puntos más para graficarlo.

Para facilitar el gráfico podemos elegir puntos que estén sobre los planos coordenados. Por ejemplo \(y = 0\;\):

\[\; \Rightarrow 2x – z = 0 \Rightarrow z = 2x\]

Entonces haciendo que \(x = 1\) debe ser \(z = 2\), y obtenemos el punto \({P_1}\left( {1,0,2} \right)\)

Para tomar otro punto del plano podemos hacer que \(z = 0\)

\[\; \Rightarrow \;2x – 3y = 0 \Rightarrow y = \frac{2}{3}x\]

Y si \(x = 3\) entonces \(y = 2\). Obtenemos el punto \({P_2}\left( {3,2,0} \right)\)

Entonces \(\beta \) contiene a los puntos \(\left( {0,0,0} \right)\;,\;\left( {1,0,2} \right)\) y \(\left( {3,2,0} \right)\):

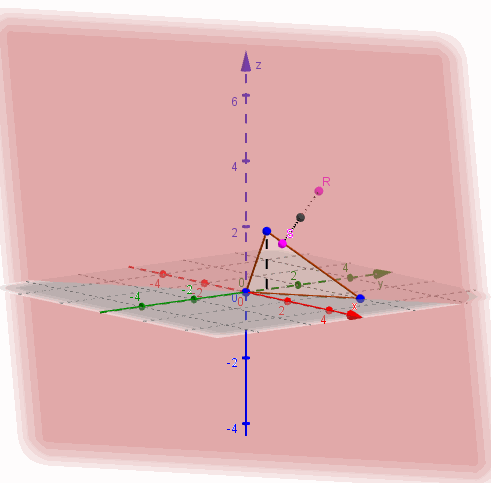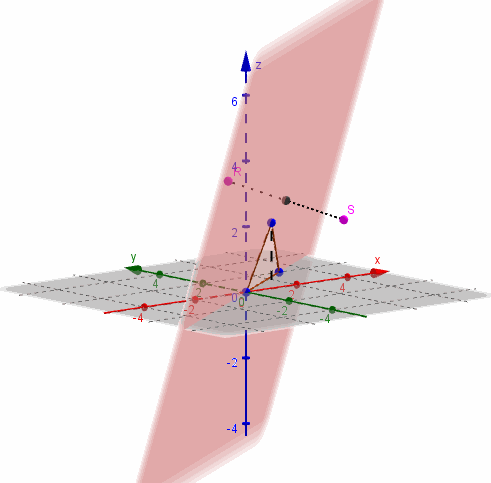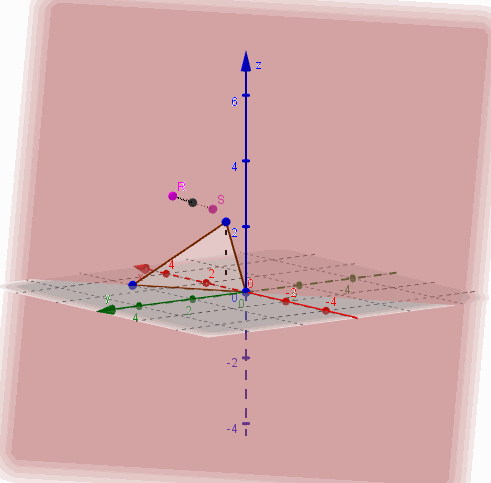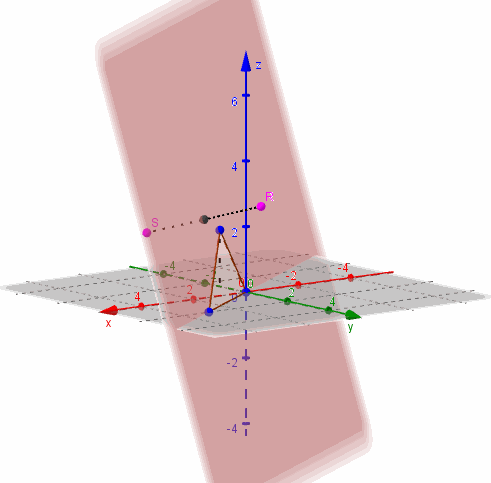
Ejemplo

Dados \(A\left( {4,5,2} \right),\;\;B\left( {1,3,4} \right)\), \(C\left( {2,2,5} \right)\) hallar, si es posible, el plano que contiene a los tres puntos.

Habíamos dicho que tres puntos no alineados determinan un único plano que los contiene.

Hagamos una figura de análisis:

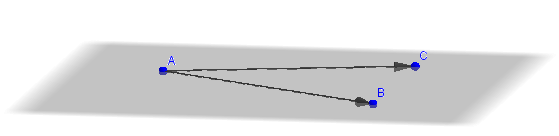
Con los tres puntos, podemos armar dos vectores, por ejemplo:

\[\overrightarrow {AB} = \left( { – 3, – 2,2} \right)\]

\[\overrightarrow {AC} = \left( { – 2, – 3,3} \right)\]

El vector normal debe ser perpendicular a ambos vectores cómo muestra la siguiente figura:

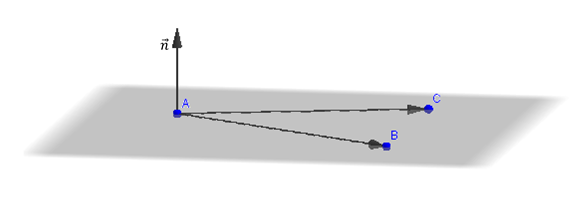
¿Qué operación nos permite hallar un vector perpendicular a otros dos?

\[(\overrightarrow {AB} \times \overrightarrow {AC} = \left( {0,5,5} \right)\]

¿Qué resultado habríamos obtenido si \(A\), \(B\) y \(C\) estuvieran alineados?

El vector \(\left( {0,5,5} \right)\) es perpendicular al plano que buscamos, entonces podemos tomar \(\vec n\;\; = \;\left( {0,5,5} \right)\) y escribir la ecuación del plano:

\[\alpha :\;\;\;5y + 5z + d = 0\]

Para hallar \(d\) podemos reemplazar cualquiera de los tres puntos. Reemplacemos \(A\):

\[5.5 + 5.2 + d = 0 \Rightarrow d = – 35\]

Luego:

\[5y + 5z – 35 = 0\]

Podemos dividir por 5 ambos miembros:

\[\alpha :\;\;\;y + z – 7 = 0\]

El lector puede comprobar que los puntos \(B\) y \(C\) verifican esta ecuación.

Busquemos las intersecciones con los ejes para graficar el plano:

\[y = z = 0 \Rightarrow – 7 = 0\;\;\;Absurdo\]

Entonces \(\alpha \) no corta al eje \(x\).

¿En qué punto corta al eje \(y\)? \(\;\left( {0,7,0} \right)\)

¿Y al eje \(z\)? \(\left( {0,0,7} \right)\)

Observemos que el plano contiene a todos los puntos de la forma \(\left( {x,7,0} \right)\) con \(x \in \mathbb{R}.\)

Lo mismo ocurre con los puntos del tipo \(\left( {x,0,7} \right)\) con \(x \in \mathbb{R}.\)

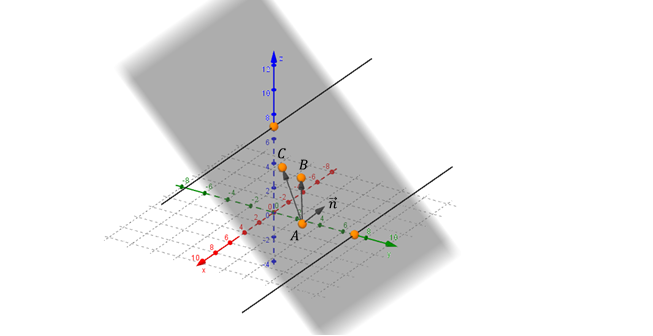
Podemos observar entonces que:

\[\;a = 0 \Rightarrow el\;plano\;es\parallel \;\;al\;eje\;x\]

Ecuación segmentaria del plano

Dada la ecuación general de un plano:

\[\pi :\;\;ax + by + cz + d = 0\]

Si \(a,b,c,d\) son distintos de cero, es posible obtener otra ecuación del plano como sigue:

\[ax + by + cz = – d\]

\[\frac{a}{{ – d}}x + \frac{b}{{ – d}}y + \frac{c}{{ – d}}z = 1\]

\[\frac{x}{{\left( { – \frac{d}{a}} \right)}} + \frac{y}{{\left( { – \frac{d}{b}} \right)}} + \frac{z}{{\left( { – \frac{d}{c}} \right)}} = 1\]

Si llamamos \(p = – \frac{d}{a}\) , \(q = – \frac{d}{b}\), \(r = – \frac{d}{c}\)

Resulta:

Veamos qué indican \(p\), \(q\) y \(r\):

¿Cuál es la intersección del plano con el eje x?

¿Cuál es la intersección con el eje y?

\[\left( {0,q,0} \right)\]

¿Y con el eje z?

\[\left( {0,0,r} \right)\]

Podemos observar que p, q y r indican las intersecciones con los ejes.

Ejemplo

\[2x – 3y + z – 6 = 0\]

\[2x – 3y + z = 6\]

\[\frac{{2x}}{6} – \frac{{3y}}{6} + \frac{z}{6} = 1\]

\[\frac{x}{3} – \frac{y}{2} + \frac{z}{6} = 1\]

Esta ecuación parece segmentaria pero no lo es por el signo negativo. La reescribimos así:

\[\frac{x}{3} + \frac{y}{{ – 2}} + \frac{z}{6} = 1\;\;\;\;\;\;\;Ecuación\;segmentaria\]

La ecuación segmentaria es práctica para graficar un plano porque muestra los tres puntos de corte con los ejes:

Ecuación vectorial paramétrica del plano

Dados dos vectores \(\vec u = \left( {{u_1},{u_2},{u_3}} \right)\) y \(\overrightarrow {v\;} = \left( {{v_1},\;{v_2},\;{v_3}} \right)\) no paralelos y un punto \({P_0}\;\left( {{x_0},\;{y_0},\;{z_0}} \right)\), nos proponemos hallar la ecuación del plano \(\pi \) que pasa por \({P_0}\)
y es paralelo a \(\overrightarrow {\;u} \) y \(\overrightarrow {v\;} \).

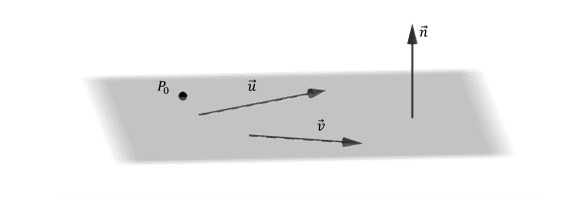
¿Cómo podemos obtener un vector perpendicular al plano conociendo dos vectores paralelos a dicho plano?

\[\vec n = \vec u \times \vec v\]

Teniendo \(\vec n\;\) y el punto \({P_0}\), podemos hallar la ecuación implícita o general del plano \(\pi \) como habíamos visto previamente.

Obtendremos a continuación otro tipo de ecuación del plano, cuya deducción se basa en el concepto de combinación lineal de vectores, tal cómo vimos en el ejemplo.

Si \(P\left( {x,y,z} \right)\) es un punto cualquiera del plano \(\pi \), los vectores \(\overrightarrow {{P_0}P} \;,\;\vec u\;\;y\;\;\;\vec v\;\) son coplanares

Entonces

\[\exists \alpha ,\beta \in \mathbb{R}\;\;|\;\;\overrightarrow {{P_0}P} = \alpha \;\vec u + \beta \;\vec v\]

Esto significa que el vector \(\overrightarrow {{P_0}P} \) puede expresarse como combinación lineal de \(\vec u\) y \(\vec v\), como se muestra en la figura:

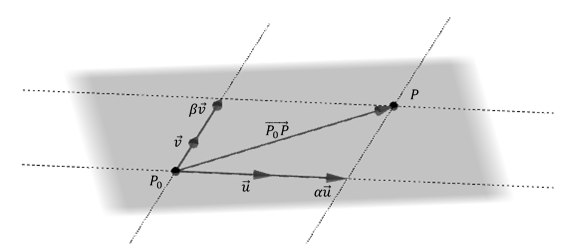
\[\left( {x – {x_0}\;,\;y – {y_0},z – {z_0}} \right) = \alpha .\left( {{u_1},{u_2},{u_3}} \right)\; + \beta \;\left( {{v_1},{v_2},{v_3}} \right)\]

Por lo tanto:

\(\left( {x,y,z} \right) = \left( {{x_0},{y_0},{z_0}} \right) + \alpha \;\left( {{u_1},{u_2},{u_3}} \right) + \beta \;\left( {{v_1},{v_2},{v_3}} \right)\),\(\;\;con\;\alpha ,\beta \in \mathbb{R}\)

O en notación vectorial:

Ejemplo

Armar la ecuación vectorial paramétrica del plano paralelo a \(\vec u = \left( {3, – 1,5} \right)\) y \(\vec v = \left( {7,3,2} \right)\) que pasa por el punto \({P_0}\left( {0, – 1,8} \right).\)

De acuerdo con lo que hemos visto, tenemos toda la información para escribir la ecuación vectorial paramétrica:

\[\left( {x,y,z} \right) = \left( {0, – 1,8} \right) + \alpha \left( {3, – 1,5} \right) + \beta \left( {7,3,2} \right)\;\;,\;\;\;con\;\alpha ,\beta \in \mathbb{R}\]

Nota: Para cada \(\alpha \;y\;\beta \in \mathbb{R}\) se obtiene un punto del plano. Por ejemplo si \(\;\alpha = 1\;\;y\;\;\;\beta = – 1\) se obtiene el punto \(\left( {x,y,z} \right) = \left( { – 4,\; – 5,\;11} \right)\).

Busquemos ahora la ecuación general de este plano.

\[\vec n = \vec u \times \vec v = \left( {3, – 1,5} \right) \times \left( {7,3,2} \right) = \left( { – 17,\;29,16} \right)\]

Luego:

\[ – 17x + 29y + 16z + d = 0\]

Reemplazamos \({P_0}\) para obtener \(d\):

\[ – 17.0 + 29.\left( { – 1} \right) + 16.8 + d = 0 \Rightarrow \;d = – 99\]

Luego:

\[ – 17x + 29y + 16z – 99 = 0\]

que es la ecuación general o implícita del plano.

De la ecuación general a la ecuación vectorial paramétrica

Dada la ecuación general de un plano, ¿cómo puede obtenerse una ecuación vectorial paramétrica de dicho plano?

Consideremos el siguiente ejemplo:

\[\omega :\;\;\;2x – y + 3z + 9 = 0\]

Podemos despejar cualquiera de las variables, por ejemplo y:

\[y = 2x + 3z + 9\]

Entonces:

\[\omega :\;\;\;\left( {x,y,z} \right) = \left( {x,\;2x + 3z + 9\;,z} \right)\;\;\]

Reescribimos como suma de tres vectores, de forma tal que uno de ellos tenga los términos con \(x\), otro los términos con \(z\) y otro los términos independientes:

\[\left( {x,y,z} \right) = \left( {x,2x,0} \right) + \left( {0,3z,z} \right) + \left( {0,9,0} \right)\;\]

\[\left( {x,y,z} \right) = x\left( {1,2,0} \right) + z\left( {0,3,1} \right) + \left( {0,9,0} \right)\;,\;con\;\;x,z \in R\;\]

Si llamamos \(x = \alpha \) , \(z = \beta \), resulta:

\[\omega :\;\;\;\left( {x,y,z} \right) = \left( {0,9,0} \right) + \alpha \left( {1,2,0} \right) + \beta \left( {0,3,1} \right)\;,\;con\;\;\alpha ,\beta \in R\;\;\]

Obtuvimos así una ecuación vectorial paramétrica del plano \(\omega .\)

El lector puede comprobar que: i) los vectores \(\vec u\) = (1,2,0) y \(\vec v\) = (0,3,1) son perpendiculares a \(\vec n\) = (2,-1,3), o sea que son paralelos al plano; ii) P₀(0,9,0) \( \in \omega \).

Videos relacionados con ecuación del plano