Rototraslación de cónicas

Diagonalización de matrices simétricas

Habíamos visto (en autovalores y autovectores) algunas propiedades de las matrices simétricas que retomaremos aquí para poder aplicarlas al estudio de las cónicas.

Si \(A \in {\mathbb{R}^{nxn}}\) es simétrica ( \(A = {A^t}\) ), entonces se verifican las siguientes propiedades:

Nota: Recordemos que \(P \in {\mathbb{R}^{n \times n}}\) es ortogonal si y sólo sí \({P^t} = {P^{ – 1}}\). Las matrices ortogonales se caracterizan porque sus columnas son vectores ortogonales y de norma (módulo) 1.

Ejemplo 2

Calculemos la diagonalización de la matriz:

\(A = \left( {\begin{array}{*{20}{c}}3&4\\4&9\end{array}} \right)\)

El lector puede verificar que sus autovalores y autoespacios son:

\[\lambda = 11\;\;\;,\;\;\;{S_{11}} = gen\left\{ {\left( {\begin{array}{*{20}{c}}1\\2\end{array}} \right)} \right\}\]

\[\lambda = 1\;\;\;,\;\;\;\;{S_1} = gen\left\{ {\left( {\begin{array}{*{20}{c}}{ – 2}\\1\end{array}} \right)} \right\}\]

Observamos que los autoespacios son ortogonales (propiedad de las simétricas). Podemos construir la matriz P (cuyas columnas son los autovectores) que permite diagonalizar \(A\) :

\[P = \left( {\begin{array}{*{20}{c}}1&{ – 2}\\2&1\end{array}} \right)\]

\[{P^{ – 1}}AP = D = \left( {\begin{array}{*{20}{c}}{11}&0\\0&1\end{array}} \right)\]

Si bien las columnas de \(P\) son ortogonales, \(P\) no es una matriz ortogonal porque sus columnas no tienen módulo 1. Nos falta normalizar los autovectores, o sea obtener sus versores asociados:

,

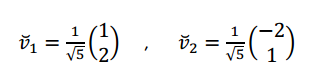
Entonces podemos diagonalizar \(A\) mediante una matriz \(Q\) ortogonal:

\[Q = \left( {\begin{array}{*{20}{c}}{\frac{1}{{\sqrt 5 }}}&{\frac{{ – 2}}{{\sqrt 5 }}}\\{\frac{2}{{\sqrt 5 }}}&{\frac{1}{{\sqrt 5 }}}\end{array}} \right)\]

Esta matriz sí verifica:

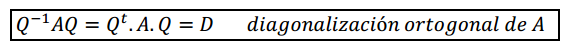
Ejercicio para el lector 1

Encontrar una matriz \(A \in {\mathbb{R}^{2 \times 2}}\) simétrica que verifique las siguientes condiciones:

\[A\left( {\begin{array}{*{20}{c}}3\\4\end{array}} \right) = \left( {\begin{array}{*{20}{c}}6\\8\end{array}} \right)\;\;\;y\;\;\;det\left( A \right) = – 2\]

Sugerencia: Tener en cuenta que \({\lambda _1}\;.{\lambda _2} = det\left( A \right)\)

Rototraslación de cónicas

Ejemplo 0

Dada la ecuación en \({\mathbb{R}^2}\): \(3{x^2} + 9{y^2} = 6\)

Podemos identificar, por los signos de los coeficientes, que corresponde a una elipse cuya ecuación canónica es:

\[\frac{{{x^2}}}{2} + \frac{{{y^2}}}{{\frac{2}{3}}} = 1\]

Ejemplo 1: una elipse rotada

Nos interesa descubrir qué curva está representada por la siguiente ecuación:

\[3{x^2} + 8xy + 9{y^2} = 6\;\;\;\;\;\;\;\;\;\left[ 1 \right]\]

Aparece en esta ecuación el término \(8xy\), denominado término rectangular o de producto cruzado.

Usamos GeoGebra para obtener la gráfica de esta cónica:

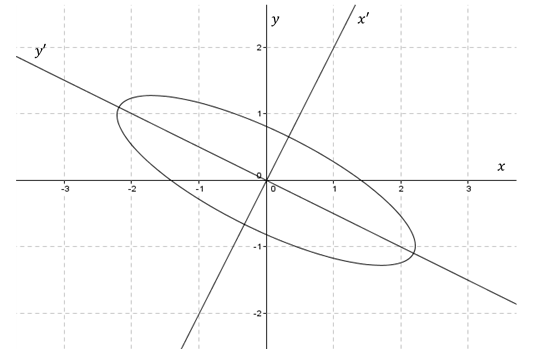
Observamos que se trata de una elipse cuyos ejes no son paralelos a los ejes coordenados. Veremos a continuación cómo hallar las direcciones de esos ejes para obtener la ecuación canónica e identificar analíticamente la cónica.

Retomemos la ecuación [1]:

\[3{x^2} + 8xy + 9{y^2} = 6\]

Esta ecuación puede expresarse matricialmente como sigue:

\[\left( {x\;\;y} \right)\left( {\begin{array}{*{20}{c}}{}&{}\\{}&{}\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = 6\]

Los coeficientes de \({x^2}\) y de \({y^2}\) van en la diagonal:

\[\left( {x\;\;y} \right)\left( {\begin{array}{*{20}{c}}3&{}\\{}&9\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = 6\]

Y el coeficiente del término rectangular se divide por dos para completar una matriz simétrica:

\[\left( {x\;\;y} \right)\left( {\begin{array}{*{20}{c}}3&4\\4&9\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = 6\;\;\;\;\;\;\;\;\;\;\;\;\left[ 1 \right]\]

Verifiquemos que efectivamente se obtiene lo mismo:

\[\left( {x\;\;y} \right)\left( {\begin{array}{*{20}{c}}3&4\\4&9\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = 6\]

\[ \Rightarrow \;\left( {3x + 4y\;\;\;\;\;4x + 9y} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = 6\]

\[ \Rightarrow \left( {3x + 4y} \right)x + \left( {4x + 9y} \right)y = 6\]

\( \Rightarrow 3{x^2} + 8xy + 9{y^2} = 6\) ¡Verificado!

La expresión \(3{x^2} + 8xy + 9{y^2}\) se denomina forma cuadrática y la matriz simétrica que la caracteriza es \(A = \left( {\begin{array}{*{20}{c}}3&4\\4&9\end{array}} \right)\).

Por ser \(A\) una matriz simétrica, es ortogonalmente diagonalizable.

Como habíamos visto en un ejemplo anterior:

\[Q = \left( {\begin{array}{*{20}{c}}{\frac{1}{{\sqrt 5 }}}&{\frac{{ – 2}}{{\sqrt 5 }}}\\{\frac{2}{{\sqrt 5 }}}&{\frac{1}{{\sqrt 5 }}}\end{array}} \right)\;\;;\;\;D = \left( {\begin{array}{*{20}{c}}{11}&0\\0&1\end{array}} \right)\]

\[{Q^t}AQ = D\]

La matriz Q, cuyas columnas son autovectores unitarios de A, representa un cambio de base como veremos a continuación.

Recordatorio sobre cambio de base

Se puede leer lo que escribimos sobre cambio de base acá.

Tomemos un par de bases del mismo espacio vectorial \(V\):

\(B = \left\{ {{v_1}, \ldots ,{v_n}} \right\}\) y \({\rm{\;}}B’ = \left\{ {{w_1}, \ldots ,{w_n}} \right\}\)

Construyamos la matriz asociada a la transformación lineal identidad:

\[M{\left( {Id} \right)_{BB{\rm{‘}}}} = \left( {{{\left[ {{v_1}} \right]}_{B’}},{\rm{\;}} \ldots ,{\rm{\;}}{{\left[ {{v_n}} \right]}_{B’}}} \right) \in {\mathbb{R}^{n \times n}}\]

Esta matriz, llamada matriz de cambio de base de \(B\) a \(B’\) , permite pasar de coordenadas en \(B\) a coordenadas en \(B’\) :

\[M{\left( {Id} \right)_{BB’}}.{\left[ v \right]_B} = {\left[ v \right]_{B’}}\]

Si consideramos las bases \(B = \left\{ {\left( {\frac{1}{{\sqrt 5 }},\frac{2}{{\sqrt 5 }}} \right),\left( { – \frac{2}{{\sqrt 5 }},\frac{1}{{\sqrt 5 }}} \right)} \right\}\) ,\(B’ = E\) (base canónica de \({\mathbb{R}^2}\)) y llamamos:

Resulta:

\[Q = M{\left( {Id} \right)_{BE}}\]

Por lo tanto:

\[Q\;{\left[ v \right]_B} = {\left[ v \right]_E}\]

\[Q\left( {\begin{array}{*{20}{c}}{x’}\\{y’}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right)\]

Trasponemos ambos miembros de la igualdad:

\[\left( {\;x\;\;\;\;\;y} \right) = \left( {x’y’} \right){Q^t}\]

Sustituimos en [1]:

\[\left( {x\;\;\;y} \right)\;A\;\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = 6\;\;\;\; \Rightarrow \;\;\left( {{x^{‘\;}}y’} \right){Q^t}AQ\left( {\begin{array}{*{20}{c}}{x’}\\{y’}\end{array}} \right) = 6\]

Como \(Q\) es ortogonal, se verifica:

\[{Q^t}AQ = {Q^{ – 1}}AQ = D\]

Y entonces la ecuación de la cónica en el nuevo sistema de coordenadas es:

\[\left( {x’y’} \right)\left( {\begin{array}{*{20}{c}}{11}&0\\0&1\end{array}} \right)\left( {\begin{array}{*{20}{c}}{x’}\\{y’}\end{array}} \right) = 6\]

\[11{x’^2} + 1{y’^2} = 6\]

Observamos que representa una elipse cuya ecuación canónica es:

\[\frac{{{{x’}^2}}}{{\frac{6}{{11}}}} + \frac{{{{y’}^2}}}{6} = 1\]

¿Cómo se grafica esta elipse?

El cambio de base que realizamos define un nuevo sistema de ejes ortogonales. Las columnas de \(Q\) indican dirección y sentido positivo de estos nuevos ejes.

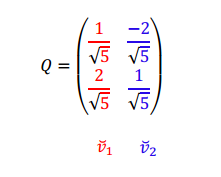
A continuación generalizaremos el método de eliminación de productos cruzados que hemos aplicado en el ejemplo anterior.

Eliminación de productos cruzados

Dada la ecuación en \({\mathbb{R}^2}\):

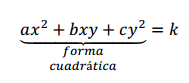
1) Buscamos la expresión matricial de la forma cuadrática:

La matriz \(A = \left( {\begin{array}{*{20}{c}}a&{\frac{b}{2}}\\{\frac{b}{2}}&c\end{array}} \right)\) es la matriz simétrica que caracteriza a la forma cuadrática.

2) Diagonalizamos ortogonalmente la matriz de la forma cuadrática:

Como la matriz es simétrica, es ortogonalmente diagonalizable. Entonces \(\exists Q\;\)ortogonal tal que \({Q^t}A\;Q = D\). La matriz \(Q\) la obtenemos con los autovectores normalizados.

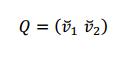
Como las columnas de \(Q\) son perpendiculares y unitarias (de norma 1), se verifica que \({Q^t} = {Q^{ – 1}}\).

3) La matriz \(Q\) hallada nos permite proponer un cambio de base o de coordenadas:

\[\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = Q\left( {\begin{array}{*{20}{c}}{x’}\\{y’}\end{array}} \right)\;\; \Rightarrow \;\;\;\left( {x\;\;\;\;y} \right) = \left( {x’y’} \right){Q^t}\]

4) Reemplazamos en [1]:

\[\left( {x’y’} \right)\left( {\begin{array}{*{20}{c}}{{\lambda _1}}&0\\0&{{\lambda _2}}\end{array}} \right)\left( {\begin{array}{*{20}{c}}{x’}\\{y’}\end{array}} \right) = k\]

Con este procedimiento pudimos eliminar el término de producto cruzado, obteniendo la ecuación de la cónica en el nuevo sistema de coordenadas.

Ejemplo 2: una hipérbola rotada

Hallar la ecuación canónica y graficar la cónica dada por la ecuación:

\[{x^2} + 4xy + {y^2} = 9\]

Resolución

El término de producto cruzado \(4xy\) indica que la cónica está rotada respecto de los ejes canónicos.

1) Buscamos la expresión matricial:
\[\left( {x\;\;y} \right)\left( {\begin{array}{*{20}{c}}1&2\\2&1\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = 9\]

2) Diagonalizamos ortogonalmente la matriz de la forma cuadrática\(A = \left( {\begin{array}{*{20}{c}}1&2\\2&1\end{array}} \right)\;:\)

Dejamos a cargo del lector comprobar que los autovalores son:

\[\lambda = – 1\;\;,\;\;\;\lambda = 3\]

Y los autoespacios:

\[{S_{ – 1}} = gen\left\{ {\left( {\begin{array}{*{20}{c}}1\\{ – 1}\end{array}} \right)} \right\}\;\;\;,\;\;\;{S_3} = gen\left\{ {\left( {\begin{array}{*{20}{c}}1\\1\end{array}} \right)} \right\}\]

Con los autovectores hallados podemos armar la matriz \(Q\) ortogonal (de columnas ortogonales y de módulo 1):

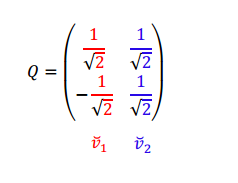
Recordemos que las columnas de \(Q\) indican la dirección y sentido positivo de los nuevos ejes e .

3) La matriz \(Q\) hallada nos permite proponer un cambio de base o de coordenadas:

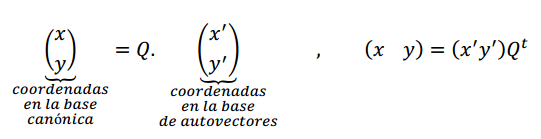
4) Reemplazamos en la expresión matricial:

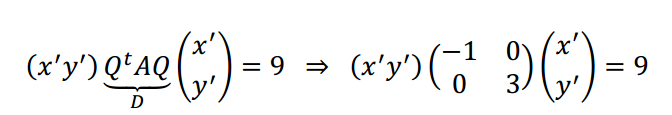
\[ – {x’^2} + 3{y’^2} = 9\]

\[ – \frac{{{{x’}^2}}}{9} + \frac{{{{y’}^2}}}{3} = 1\]

Ésta es la ecuación canónica de una hipérbola de eje focal \(y’\), cuya gráfica es:

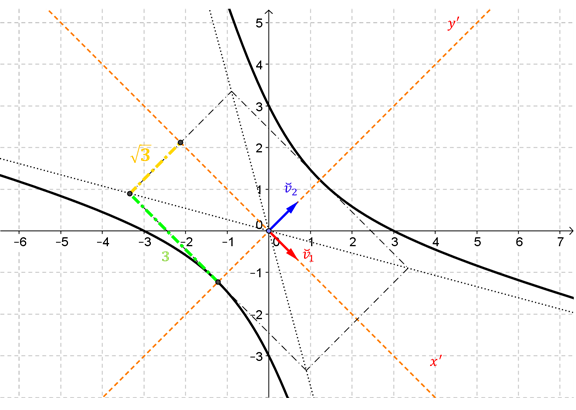
¿Cuáles son las coordenadas de los vértices de la hipérbola respecto de la base canónica?

Las bases de los dos sistemas de coordenadas que estamos utilizando son:

\[B = \left\{ {\left( {\begin{array}{*{20}{c}}1\\0\end{array}} \right),\left( {\begin{array}{*{20}{c}}0\\1\end{array}} \right)} \right\}\;\;\;\;\;,\;\;\;\;\;\;\;B’ = \left\{ {\left( {\begin{array}{*{20}{c}}{\frac{1}{{\sqrt 2 }}}\\{ – \frac{1}{{\sqrt 2 }}}\end{array}} \right),\left( {\begin{array}{*{20}{c}}{\frac{1}{{\sqrt 2 }}}\\{\frac{1}{{\sqrt 2 }}}\end{array}} \right)} \right\}\]

De la ecuación canónica se deduce:

Coordenadas de los vértices en \(B’ = \pm \left( {\begin{array}{*{20}{c}}0\\{\sqrt 3 }\end{array}} \right)\)

Realicemos el cambio de coordenadas:

\[\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = Q\left( {\begin{array}{*{20}{c}}{x’}\\{y’}\end{array}} \right)\;\;\;\;\; \Rightarrow \;\;\;\;\;\;\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{\frac{1}{{\sqrt 2 }}}&{\frac{1}{{\sqrt 2 }}}\\{ – \frac{1}{{\sqrt 2 }}}&{\frac{1}{{\sqrt 2 }}}\end{array}} \right)\left( {\begin{array}{*{20}{c}}0\\{ \pm \sqrt 3 }\end{array}} \right) = \pm \left( {\begin{array}{*{20}{c}}{\frac{{\sqrt 3 }}{{\sqrt 2 }}}\\{\frac{{\sqrt 3 }}{{\sqrt 2 }}}\end{array}} \right)\]

Éstas son las coordenadas de los vértices de la hipérbola respecto de la base canónica.

Ejercicio para el lector 2

Dada la ecuación:

\(\left( {\begin{array}{*{20}{c}}x&y\end{array}} \right)A\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = 4\)   con   \(A = \left( {\begin{array}{*{20}{c}}2&2\\2&5\end{array}} \right)\)

a) Obtener la ecuación canónica e identificar la cónica correspondiente. ¿Cuál es la dirección del eje focal de dicha cónica?

b) Considerando la misma \(A\), analizar qué lugar geométrico representa la ecuación \(\left( {\begin{array}{*{20}{c}}x&y\end{array}} \right)\;A\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = k\) para: \(k > 0\;,\;\;k = 0\;\;,\;\;k < 0\)

Ejemplo 3: roto-traslación de una cónica

Consideremos la siguiente ecuación:

\[{x^2} + 4xy + {y^2} + 6x – 9y = 9\]

Nos interesa saber qué cónica representa y graficarla.

El término de producto cruzado señala que la cónica está rotada respecto de los ejes canónicos.

Además, como habíamos visto en la unidad anterior, los términos lineales indican que posiblemente sea necesario realizar una traslación (completando cuadrados) para identificar y graficar la cónica.

1) Buscamos la expresión matricial:

\[\left( {x\;\;y} \right)\left( {\begin{array}{*{20}{c}}1&2\\2&1\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) + \left( {6\;\; – 9} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = 9\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ 1 \right]\]

Les sugerimos comprobar que se obtiene la ecuación dada.

Generalizando, la escritura matricial de los términos lineales es la siguiente:

\[dx + ey = \left( {d\;\;\;\;\;\;e} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right)\]

2) Diagonalizamos ortogonalmente la matriz de la forma cuadrática \(A = \left( {\begin{array}{*{20}{c}}1&2\\2&1\end{array}} \right)\)

3) La matriz \(Q\) hallada nos permite proponer un cambio de base o de coordenadas:

Estos dos pasos ya se hicieron en el ejemplo anterior, siendo:

\(Q = \left( {\begin{array}{*{20}{c}}{\frac{1}{{\sqrt 2 }}}&{\frac{1}{{\sqrt 2 }}}\\{–\frac{1}{{\sqrt 2 }}}&{\frac{1}{{\sqrt 2 }}}\end{array}} \right)\)    ,    \({\rm{\;}}D = \left( {\begin{array}{*{20}{c}}{–1}&0\\0&3\end{array}} \right)\)

\[\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = Q.\left( {\begin{array}{*{20}{c}}{x’}\\{y’}\end{array}} \right)\;\;\;\;\;\; \Rightarrow \;\;\;\;\left( {x\;\;\;y} \right) = \left( {x’y’} \right){Q^t}\]

4) Reemplazamos en la expresión matricial [1]:

\[\left( {x’y’} \right){Q^t}AQ\left( {\begin{array}{*{20}{c}}{x’}\\{y’}\end{array}} \right) + \left( {6\;\; – 9} \right)\;Q\left( {\begin{array}{*{20}{c}}{x’}\\{y’}\end{array}} \right)\]

\[\left( {x’y’} \right)\left( {\begin{array}{*{20}{c}}{ – 1}&0\\0&3\end{array}} \right)\left( {\begin{array}{*{20}{c}}{x’}\\{y’}\end{array}} \right) + \left( {6\;\; – 9} \right)\left( {\begin{array}{*{20}{c}}{\frac{1}{{\sqrt 2 }}}&{\frac{1}{{\sqrt 2 }}}\\{ – \frac{1}{{\sqrt 2 }}}&{\frac{1}{{\sqrt 2 }}}\end{array}} \right)\left( {\begin{array}{*{20}{c}}{x’}\\{y’}\end{array}} \right)\]

\[\left( {{x^{‘\;}}y’} \right)\left( {\begin{array}{*{20}{c}}{ – 1}&0\\0&3\end{array}} \right)\left( {\begin{array}{*{20}{c}}{x’}\\{y’}\end{array}} \right) + \left( {\frac{{15}}{{\sqrt 2 }}\;\;\;\;\;\; – \frac{3}{{\sqrt 2 }}} \right).\left( {\begin{array}{*{20}{c}}{x’}\\{y’}\end{array}} \right)\]

\[ – {x’^2} + 3{y’^2} + \frac{{15}}{{\sqrt 2 }}x’ – \frac{3}{{\sqrt 2 }}y’ = 9\]

Observamos que los términos lineales se modifican por el cambio de base realizado.

Hasta aquí, pudimos eliminar el término de producto cruzado definiendo un nuevo sistema de ejes paralelos a los ejes de la cónica.

5) Efectuamos una traslación para obtener la ecuación canónica.

Tal como habíamos visto en la unidad anterior, el método de completar cuadrados nos permite ubicar el centro o el vértice de la cónica y obtener su ecuación canónica.

\[ – {x’^2} + \frac{{15}}{{\sqrt 2 }}x’ + 3{y’^2} – \frac{3}{{\sqrt 2 }}y’ = 9\]

\[ – \left[ {{{\left( {x’ – \frac{{15}}{{2\sqrt 2 }}} \right)}^2} – {{\left( {\frac{{15}}{{2\sqrt 2 }}} \right)}^2}} \right] + 3\left[ {{{\left( {y’ – \frac{1}{{2\sqrt 2 }}} \right)}^2} – {{\left( {\frac{1}{{2\sqrt 2 }}} \right)}^2}} \right] = 9\]

\[ – \left[ {{{\left( {x’ – \frac{{15}}{{2\sqrt 2 }}} \right)}^2} – \frac{{225}}{8}} \right] + 3\left[ {{{\left( {y’ – \frac{1}{{2\sqrt 2 }}} \right)}^2} – \frac{1}{8}} \right] = 9\]

\[ – {\left( {x’ – \frac{{15}}{{2\sqrt 2 }}} \right)^2} + \frac{{225}}{8} + 3{\left( {y’ – \frac{1}{{2\sqrt 2 }}} \right)^2} – \frac{3}{8} = 9\]

\[ – {\left( {x’ – \frac{{15}}{{2\sqrt 2 }}} \right)^2} + 3{\left( {y’ – \frac{1}{{2\sqrt 2 }}} \right)^2} = – \frac{{75}}{4}\]

\[\frac{{{{\left( {x’ – \frac{{15}}{{2\sqrt 2 }}} \right)}^2}}}{{\frac{{75}}{4}}} – \frac{{{{\left( {y’ – \frac{1}{{2\sqrt 2 }}} \right)}^2}}}{{\frac{{25}}{4}}} = 1\]

Obtuvimos la ecuación ordinaria de una hipérbola que tiene las siguientes características:

1. Está rotada respecto de los ejes canónicos. Las direcciones y sentidos positivos de los nuevos ejes \(x’\;y’\;\) están dadas por las columnas de \(Q\), como habíamos visto.

2. De acuerdo con los signos en la ecuación, el eje focal es paralelo al eje \(x’\).

3. Las coordenadas del centro de la hipérbola en el sistema \(x’\;y’\) son:

\[\alpha = \frac{{15}}{{2\sqrt 2 }}\;\;\;;\;\;\;\beta = \frac{1}{{2\sqrt 2 }}\]

Para obtener la ecuación canónica, planteamos las ecuaciones de traslación:

\[\left\{ {\begin{array}{*{20}{c}}{x» = x’ – \frac{{15}}{{2\sqrt 2 }}}\\{y» = y’ – \frac{1}{{2\sqrt 2 }}}\end{array}} \right.\]

\[ \Rightarrow \;\;\;\frac{{{{x»}^2}}}{{\frac{{75}}{4}}} – \frac{{{{y»}^2}}}{{\frac{{25}}{4}}} = 1\]

\[semieje\;real = \frac{{5\sqrt 3 }}{2} \cong 4,33\;\;\;\;\;\;\;,\;\;\;\;\;semieje\;imaginario = \frac{5}{2} = 2,5\]

Con esta información podemos realizar un gráfico aproximado de la hipérbola. Primero indicaremos los tres sistemas de ejes:

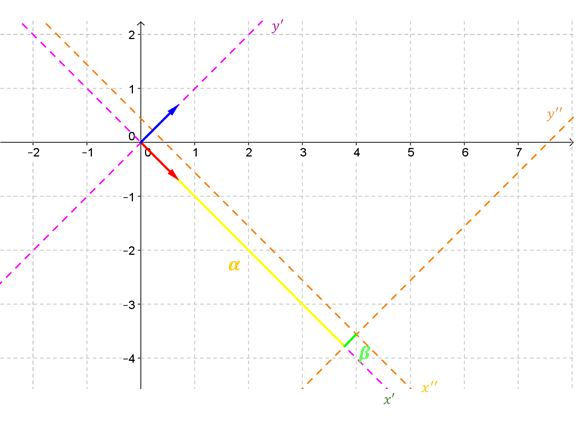
Ahora ya podemos realizar la gráfica de la hipérbola:

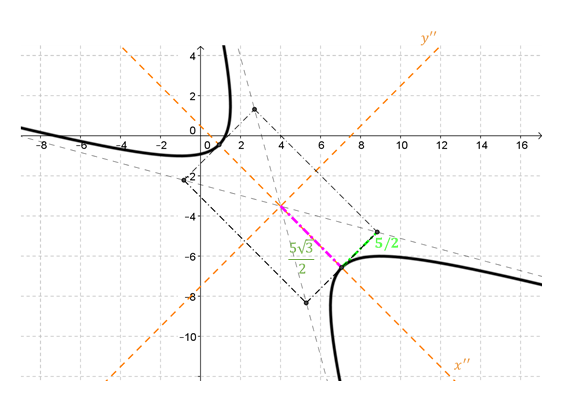
¿Cómo podríamos hallar las coordenadas del centro de la hipérbola respecto de la base canónica?

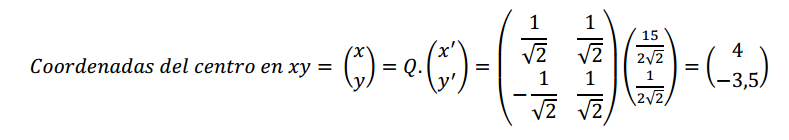
Ejemplo 4: rototraslación de una parábola

Consideremos la ecuación:

\[{x^2} – 2xy + {y^2} + \sqrt 2 x – 2\sqrt 2 y = 0\]

Nos interesa hallar la ecuación canónica y graficar la cónica correspondiente.

Resolución

1) Escribimos la forma cuadrática matricialmente:

\[\left( {x\;\;y} \right)\left( {\begin{array}{*{20}{c}}1&{ – 1}\\{ – 1}&1\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) + \left( {\sqrt 2 \;\;\;\;\;\; – 2\sqrt 2 } \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = 0\;\;\;\;\;\left[ 1 \right]\]

2) Diagonalizamos ortogonalmente y planteamos las ecuaciones de rotación:

\[Q = \left( {\begin{array}{*{20}{c}}{\frac{1}{{\sqrt 2 }}}&{ – \frac{1}{{\sqrt 2 }}}\\{\frac{1}{{\sqrt 2 }}}&{\frac{1}{{\sqrt 2 }}}\end{array}} \right)\;\;\;,\;\;\;D = \left( {\begin{array}{*{20}{c}}0&0\\0&2\end{array}} \right)\;\;\;,\;\;\]

3) La matriz \(Q\) hallada nos permite proponer un cambio de base o de coordenadas:

\[\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = Q\left( {\begin{array}{*{20}{c}}{x’}\\{y’}\end{array}} \right)\;\;\;,\;\;\;\;\left( {x\;\;\;\;y} \right) = \left( {x’y’} \right){Q^t}\]

4) Reemplazamos en [1]:

\[\left( {x’y’} \right)\left( {\begin{array}{*{20}{c}}0&0\\0&2\end{array}} \right)\left( {\begin{array}{*{20}{c}}{x’}\\{y’}\end{array}} \right) + \left( {\sqrt 2 \;\;\;\;\;\; – 2\sqrt 2 } \right)\left( {\begin{array}{*{20}{c}}{\frac{1}{{\sqrt 2 }}}&{ – \frac{1}{{\sqrt 2 }}}\\{\frac{1}{{\sqrt 2 }}}&{\frac{1}{{\sqrt 2 }}}\end{array}} \right)\left( {\begin{array}{*{20}{c}}{x’}\\{y’}\end{array}} \right) = 0\]

\[\left( {0\;\;\;\;\;2y’} \right)\left( {\begin{array}{*{20}{c}}{x’}\\{y’}\end{array}} \right) + \left( { – 1\;\;\;\;\;\; – 3} \right)\left( {\begin{array}{*{20}{c}}{x’}\\{y’}\end{array}} \right) = 0\]

\[2{y’^2} – x’ – 3y’ = 0\]

Cómo aparece \({y’^2}\) y no aparece \({x’^2}\) suponemos que será una parábola.

Trataremos de expresarlo como\({\left( {y’ – \beta } \right)^2} = 4c\left( {x’ – \alpha } \right)\):

\[2{y’^2} – 3y’ = x’\]

\[2\left[ {{{y’}^2} – \frac{3}{2}y’} \right] = x’\]

\[2\left[ {{{\left( {y’ – \frac{3}{4}} \right)}^2} – {{\left( {\frac{3}{4}} \right)}^2}} \right] = x’\]

\[2{\left( {y’ – \frac{3}{4}} \right)^2} = x’ + \frac{9}{8}\]

\[{\left( {y’ – \frac{3}{4}} \right)^2} = \frac{1}{2}\left( {x’ + \frac{9}{8}} \right)\]

\[\alpha = – \frac{9}{8}\;\;\;;\;\;\;\beta = \frac{3}{4}\]

Ahora realizamos un gráfico de la parábola indicando los tres sistemas de ejes:

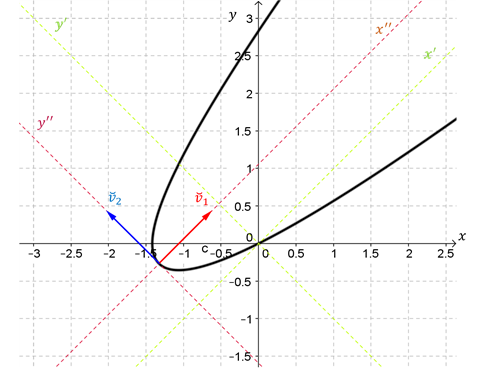
Cómo \(4c = \frac{1}{2} > 0\), la parábola se abre hacia el semieje positivo de \(x»\).

Le proponemos al lector que busque las coordenadas del vértice en la base canónica.

Ejercicio para el lector 3

Sea \(A = \left( {\begin{array}{*{20}{c}}2&2\\2&5\end{array}} \right)\), obtener la ecuación canónica y graficar la cónica dada por la ecuación:

\[\left( {\begin{array}{*{20}{c}}x&y\end{array}} \right)\;A\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) + \left( {\begin{array}{*{20}{c}}0&{6\sqrt 5 }\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = 1\]

Nota: ver ejercicio para el lector 2, la matriz \(A\) es la misma.

Clasificación de las cónicas según autovalores

Sea la ecuación en \({\mathbb{R}^2}\):

\(\left( {\begin{array}{*{20}{c}}x&y\end{array}} \right)\;A\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) + \left( {d\;\;\;\;e} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) + f = 0\;\;\;\;\;\;\;\;\;\;\;\) con \(A \in {\mathbb{R}^{2 \times 2}}\) simétrica

De acuerdo con los diferentes ejemplos desarrollados, podemos concluir que los autovalores de la matriz \(A\) permiten identificar el lugar geométrico correspondiente:

¿Rotación pura o composición de rotación y simetría?

Al diagonalizar una matriz simétrica de \({\mathbb{R}^{2 \times 2}}\) se obtienen dos autovectores ortogonales. ¿Qué efecto tiene el orden de los autovectores en la matriz \(Q\) sobre el nuevo sistema de ejes?

Veamos las diferencias entre los desarrollos indicados en cada columna:

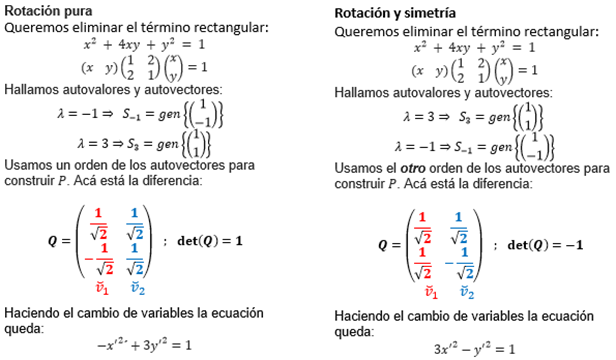
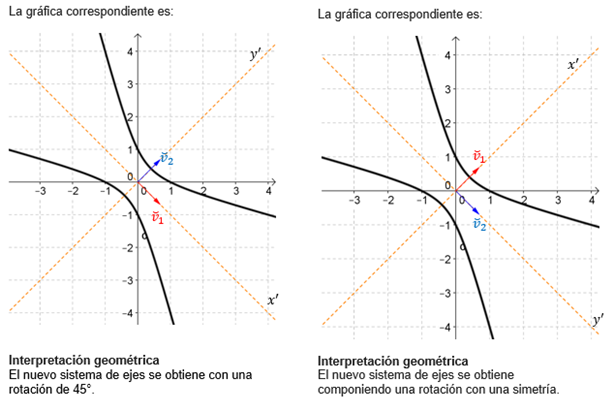
A los fines de eliminar el término rectangular para reconocer la cónica, cualquiera de las dos formas es válida. Pero es usual trabajar con una matriz \(Q\) tal que \(\det \left( Q \right) = 1\), que caracteriza a una rotación pura.

Ejercicio para el lector 4

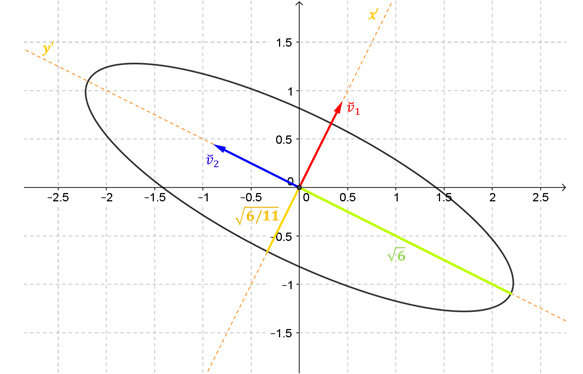
En el siguiente gráfico se ven las direcciones de los ejes y la medida del semieje mayor y semieje menor de una elipse rotada:

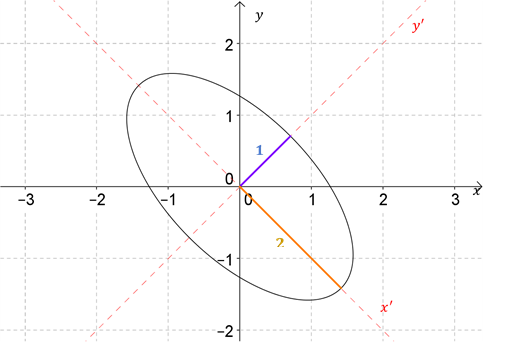
Tomando la información proporcionada en el gráfico, se pide hallar la ecuación de la elipse en términos de \(x\) e \(y\).

Sugerencia: pensar que se trata de resolver el problema inverso al habitual.

Videos relacionados con Rototraslación