Matrices y sistemas de ecuaciones lineales

Introducción

Habíamos visto que una recta en \({\mathbb{R}^3}\) puede definirse a través de un sistema de 2 ecuaciones lineales con 3 incógnitas. Por ejemplo:

\[r:\;\left\{ {\begin{array}{*{20}{c}}{x + z = 1}\\{x – y – z = 3}\end{array}} \right.\]

Este sistema puede expresarse de un modo sencillo como un producto de matrices, como sigue:

\[\left( {\begin{array}{*{20}{c}}1&0&1\\1&{ – 1}&{ – 1}\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\y\\z\end{array}} \right) = \left( {\begin{array}{*{20}{c}}1\\3\end{array}} \right)\]

Donde \(A = \left( {\begin{array}{*{20}{c}}1&0&1\\1&{ – 1}&{ – 1}\end{array}} \right) \in {\mathbb{R}^{2 \times 3}}\) es la matriz de coeficientes del sistema.

Generalizando, dado un sistema de \(m\) ecuaciones lineales con \(n\) incógnitas:

\[\left\{ {\begin{array}{*{20}{c}}{{a_{11}}\;{x_1} + {a_{12}}\;{x_2} + \ldots + {a_{1n}}\;{x_n} = {b_1}}\\{{a_{21}}\;{x_1} + {a_{22}}\;{x_2} + \ldots + {a_{2n}}\;{x_n} = {b_2}}\\ \ldots \\ \ldots \\ \ldots \\{{a_{m1}}\;{x_1} + {a_{m2}}\;{x_2} + \ldots + {a_{mn}}\;{x_n} = {b_m}}\end{array}} \right.\]

dicho sistema puede ser expresado mediante un producto de matrices:

\[\left( {\begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}& \ldots &{{a_{1n}}}\\{{a_{21}}}&{{a_{22}}}& \ldots &{{a_{2n}}}\\ \vdots & \vdots & \ddots & \vdots \\{{a_{m1}}}&{{a_{m2}}}& \ldots &{{a_{mn}}}\end{array}} \right)\;\left( {\begin{array}{*{20}{c}}{{x_1}}\\{{x_2}}\\ \vdots \\{{x_n}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{{b_1}}\\{{b_2}}\\ \vdots \\{{b_m}}\end{array}} \right)\]

siendo:

\(A = \left( {\begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}& \ldots &{{a_{1n}}}\\{{a_{21}}}&{{a_{22}}}& \ldots &{{a_{2n}}}\\ \vdots & \vdots & \ddots & \vdots \\{{a_{m1}}}&{{a_{m2}}}& \ldots &{{a_{mn}}}\end{array}} \right) \in {\mathbb{R}^{{\rm{mxn}}}}\) la matriz de coeficientes del sistema,

\(X = \left( {\begin{array}{*{20}{c}}{{x_1}}\\{{x_2}}\\ \vdots \\{{x_n}}\end{array}} \right) \in {\mathbb{R}^{{\rm{nx}}1}}{\rm{\;}}\) la matriz columna de las incógnitas, y

\(B = \left( {\begin{array}{*{20}{c}}{{b_1}}\\{{b_2}}\\ \vdots \\{{b_m}}\end{array}} \right) \in {\mathbb{R}^{{\rm{mx}}1}}\) la columna de los términos independientes.

Por lo tanto, la expresión matricial de un sistema de ecuaciones lineales es:

\[AX = B\]

Si \(\;B = O\) , el sistema se llama homogéneo.

Repaso de SCD, SCI Y SI

Los sistemas de ecuaciones lineales pueden tener una única solución (sistema compatible determinado), infinitas soluciones (sistema compatible indeterminado), o bien pueden no admitir solución (sistema incompatible).

Los sistemas homogéneos siempre son compatibles porque admiten al menos la solución trivial \(X = O\) .

Sistemas de ecuaciones lineales y determinantes

Consideremos el caso particular de los «sistemas cuadrados» (\(n\) ecuaciones con \(n\) incógnitas), cuya matriz de coeficientes es de \(n\times n\). Su expresión matricial es:

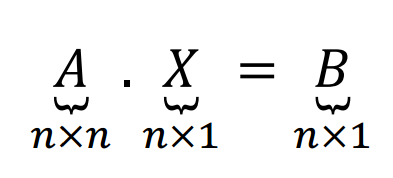
Si \({\rm{det}}\left( A \right) \ne 0\), \(A\) es inversible. Multiplicando ambos miembros por \({A^{ – 1}}\) se obtiene:

\[\;\;{A^{ – 1}}A\;X = {A^{ – 1}}B\]

\[ \Rightarrow \;\;\;X = {A^{ – 1}}B\]

Como la inversa de una matriz es única, entonces el sistema tiene una única solución \(X = {A^{ – 1}}B\).

En conclusión, dado un sistema de ecuaciones lineales \(AX = B\), con \(A \in {\mathbb{R}^{n \times n}}\):

Ejemplo

Exprese el siguiente sistema de ecuaciones lineales como una ecuación matricial de la forma \(AX = B\):

\[\left\{ {\begin{array}{*{20}{c}}{ – {x_1} + 2{x_3} = 1}\\{{x_1} – {x_2} = – 2}\\{{x_2} + {x_3} = – 1}\end{array}} \right.\]

Resolución

El sistema lo podemos expresar como:

\[\;\;\;\;\;\;\left( {\begin{array}{*{20}{c}}{ – 1}&0&2\\1&{ – 1}&0\\0&1&1\end{array}} \right)\left( {\begin{array}{*{20}{c}}{{x_1}}\\{\begin{array}{*{20}{c}}{{x_2}}\\{{x_3}}\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}1\\{\begin{array}{*{20}{c}}{ – 2}\\{ – 1}\end{array}}\end{array}} \right)\]

Calculemos el determinante de \(A\) por la fila 3:

\[\det \left( A \right) = 0.{\left( { – 1} \right)^{3 + 1}}\left| {\begin{array}{*{20}{c}}0&2\\{ – 1}&0\end{array}} \right| + 1.{\left( { – 1} \right)^{3 + 2}}\left| {\begin{array}{*{20}{c}}{ – 1}&2\\1&0\end{array}} \right| + 1.{\left( { – 1} \right)^{3 + 3}}\left| {\begin{array}{*{20}{c}}{ – 1}&0\\1&{ – 1}\end{array}} \right| = 2 + 1 = 3\]

Como el determinante de \(A\) es distinto de \(0\), podemos hallar \({A^{ – 1}}\):

\[{A^{ – 1}} = \frac{1}{{\det \left( A \right)}}{\left( {\begin{array}{*{20}{c}}{ – 1}&{ – 1}&1\\2&{ – 1}&1\\2&2&1\end{array}} \right)^T} = \frac{1}{3}\;\left( {\begin{array}{*{20}{c}}{ – 1}&2&2\\{ – 1}&{ – 1}&2\\1&1&1\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{ – \frac{1}{3}}&{\frac{2}{3}}&{\frac{2}{3}}\\{ – \frac{1}{3}}&{ – \frac{1}{3}}&{\frac{2}{3}}\\{\frac{1}{3}}&{\frac{1}{3}}&{\frac{1}{3}}\end{array}} \right)\]

Como vimos previamente, la solución será:

\[\;X = {A^{ – 1}}B\]

\[X = \left( {\begin{array}{*{20}{c}}{ – \frac{1}{3}}&{\frac{2}{3}}&{\frac{2}{3}}\\{ – \frac{1}{3}}&{ – \frac{1}{3}}&{\frac{2}{3}}\\{\frac{1}{3}}&{\frac{1}{3}}&{\frac{1}{3}}\end{array}} \right)\left( {\begin{array}{*{20}{c}}1\\{\begin{array}{*{20}{c}}{ – 2}\\{ – 1}\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{ – \frac{7}{3}}\\{ – \frac{1}{3}}\\{ – \frac{2}{3}}\end{array}} \right)\]

Ejemplo

Consideremos el siguiente sistema:

\[\left\{ {\begin{array}{*{20}{c}}{x + 2y – z = 1}\\{ – x + y + 2z = 3}\\{x + 5y = 5}\end{array}} \right.\]

¿Qué representa geométricamente cada ecuación? Un plano.

¿Qué representa geométricamente la solución del sistema de ecuaciones? La intersección entre tres planos.

¿Cómo puede ser la intersección entre dos planos? Y entonces, ¿cómo es esperable que sea la intersección entre tres planos?

\[\left( {\begin{array}{*{20}{c}}1&2&{ – 1}\\{ – 1}&1&2\\1&5&0\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\{\begin{array}{*{20}{c}}y\\z\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}1\\{\begin{array}{*{20}{c}}3\\5\end{array}}\end{array}} \right)\]

Como \(\det \left( A \right) = 0\) , no podemos resolver el sistema mediante la matriz inversa. El sistema no es compatible determinado. Pero…. ¿podemos afirmar que no tiene solución?

Podría ocurrir que el sistema tuviera infinitas soluciones o que fuera incompatible. Para analizar esas alternativas utilizaremos el método de eliminación de Gauss.

Recordemos que las operaciones elementales entre filas son:

• Multiplicar una fila por un número diferente de cero
• Permutar filas
• Sumarle a una fila un múltiplo de otra

Estas operaciones transforman un sistema en otro equivalente que tiene el mismo conjunto solución:

\[\left( {\begin{array}{*{20}{c}}1&2&{ – 1}&1\\{ – 1}&1&2&3\\1&5&0&5\end{array}} \right)\overrightarrow {{F_3} \to {F_3} – {F_1}} \;\left( {\begin{array}{*{20}{c}}1&2&{ – 1}&1\\{ – 1}&1&2&3\\0&3&1&4\end{array}} \right)\]

\[\overrightarrow {{F_2} \to {F_2} + {F_1}} \left( {\begin{array}{*{20}{c}}1&2&{ – 1}&1\\0&3&1&4\\0&3&1&4\end{array}} \right)\;\overrightarrow {{F_3} \to {F_3} – {F_2}} \;\left( {\begin{array}{*{20}{c}}1&2&{ – 1}&1\\0&3&1&4\\0&0&0&0\end{array}} \right)\]

Entonces un sistema de ecuaciones equivalente (tiene el mismo conjunto solución) y simplificado es:

\[\left\{ {\begin{array}{*{20}{c}}{x + 2y – z = 1}\\{3y + z = 4}\end{array}} \right.\;\; \Rightarrow \left\{ {\begin{array}{*{20}{c}}{x = 1 + z – 2y}\\{z = 4 – 3y}\end{array}} \right.\;\; \Rightarrow \left\{ {\begin{array}{*{20}{c}}{x = 1 + 4 – 3y – 2y = 5 – 5y}\\{z = 4 – 3y}\end{array}} \right.\;\]

\[ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{x = 5 – 5y}\\{z = 4 – 3y}\end{array}} \right.\]

Entonces la solución es:

\[S = \left\{ {\left( {x,y,z} \right) \in {\mathbb{R}^3}\;|\;x = 5 – 5y\;\;\;,\;\;\;\;z = 4 – 3y} \right\} = \left\{ {\left( {5 – 5y,y,4 – 3y} \right) \in {\mathbb{R}^3}\;\;|\;\;\;y \in \mathbb{R}} \right\}\]

\[\left( {5 – 5y,y,4 – 3y} \right) = \left( {5,0,4} \right) + \left( { – 5y,y, – 3y} \right) = \left( {5,0,4} \right) + y\left( { – 5,1, – 3} \right)\]

Si llamamos \(y = \lambda \) , resulta:

\[\left( {x,y,z} \right) = \left( { – 5,0,4\;} \right) + \lambda \left( { – 5,1, – 3} \right)\;\;\;\;,\;\;\;\lambda \in \;\mathbb{R}\]

Como el conjunto solución es una recta, podemos concluir que los tres planos pasan por la misma recta, o sea pertenecen al mismo haz de planos.

Ejemplo

Dado un sistema tal que \(\det \left( A \right) = 0\) , ¿podemos afirmar que admite infinitas soluciones?

Veamos el siguiente ejemplo en el cual la matriz de los coeficientes es la misma que en el ejemplo anterior:

\[\left\{ {\begin{array}{*{20}{c}}{x + 2y – z = 1}\\{ – x + y + 2z = 3}\\{x + 5y = 0}\end{array}} \right.\]

Resolvamos con el método de Gauss:

\[\left( {\begin{array}{*{20}{c}}1&2&{ – 1}&1\\{ – 1}&1&2&3\\1&5&0&0\end{array}} \right)\overrightarrow {{F_3} \to {F_3} – {F_1}} \;\left( {\begin{array}{*{20}{c}}1&2&{ – 1}&1\\{ – 1}&1&2&3\\0&3&1&{ – 1}\end{array}} \right)\]

\[\overrightarrow {{F_2} \to {F_2} + {F_1}} \left( {\begin{array}{*{20}{c}}1&2&{ – 1}&1\\0&3&1&4\\0&3&1&{ – 1}\end{array}} \right)\;\overrightarrow {{F_3} \to {F_3} – {F_2}} \;\left( {\begin{array}{*{20}{c}}1&2&{ – 1}&1\\0&3&1&4\\0&0&0&{ – 5}\end{array}} \right)\]

La lectura de la tercera fila implica que \(0 = – 5\). Este absurdo significa que el sistema de ecuaciones no tiene solución.

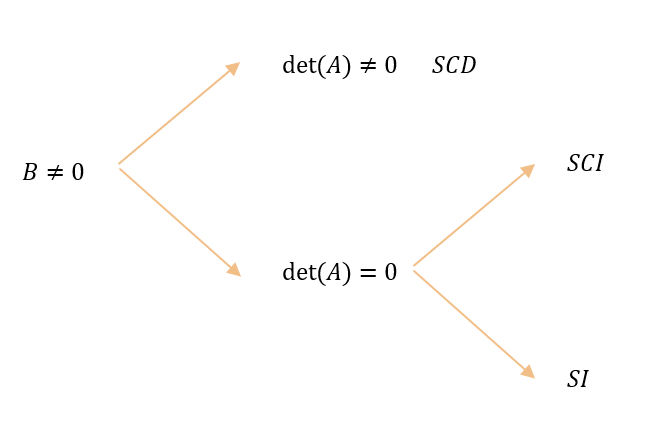
En los ejemplos anteriores observamos que si el determinante de la matriz de coeficientes es igual a cero, el sistema puede ser compatible indeterminado o incompatible.

Caso particular: Sistemas cuadrados homogéneos

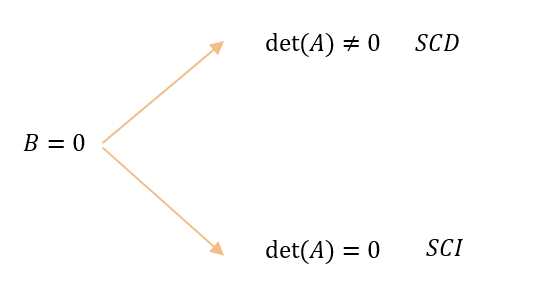
Recordemos que todo sistema homogéneo es compatible porque admite al menos la solución trivial \(X = O\) . En este caso, el determinante permite clasificar el sistema.

Dado un sistema homogéneo \(AX = O\;\;\;\;,\;\;con\;\;A \in {\mathbb{R}^{nxn}}\), puede afirmarse que:

\[\det \left( A \right) \ne \;0\;\; \Rightarrow \;SCD\]

\[\det \left( A \right) = 0\;\; \Rightarrow \;\;SCI\;\;\]

Resumen: Clasificación de un sistema \(n \times n\) por determinantes.

Dado un sistema de ecuaciones lineales \(AX = B\) , con \(A \in {\mathbb{R}^{n \times n}}\):

 

Si el sistema de ecuaciones lineales es homogéneo:

Ejemplo

Dadas \(A = \left( {\begin{array}{*{20}{c}}1&1&0\\0&2&{3k}\\3&k&{ – 3}\end{array}} \right)\;\;y\;\;B = \left( {\begin{array}{*{20}{c}}2\\2\\4\end{array}} \right)\) , hallar todos los valores de k para los cuales:

a) el sistema \(AX = O\) admite infinitas soluciones;

b) el sistema \(AX = B\) admite infinitas soluciones.

Resolución

a) Como el sistema es homogéneo, \(\det \left( A \right) = 0 \Rightarrow SCI\)

\[\det \left( A \right) =  – 3{k^2} + 9k – 6 = 0 \Leftrightarrow k = 1 \vee k = 2\]

Por lo tanto, el sistema admite infinitas soluciones para \(k = 1\;\; \vee \;\;k = 2\).

b) En este caso el sistema no es homogéneo, por lo tanto el determinante no permite decidir si el sistema es compatible indeterminado. Les proponemos que resuelvan el sistema y respondan la pregunta.

Ejercicio para el lector 7

Sean el plano \(\pi :\;\;x + y – 2 = 0\) y la recta \(r\;:\;\left\{ {\;\begin{array}{*{20}{c}}{2y + 3kz – 2 = 0}\\{3x + ky – 3z – 4 = 0}\end{array}} \right.\)

Obtener los valores de k para los cuales:

a) la recta corta al plano en un único punto;

b) la recta no interseca al plano;

c) la recta está incluida en el plano.

Sugerencia: Este ejercicio puede responderse sin hacer cálculos, teniendo en cuenta los resultados del ejemplo anterior.