Autovalores y autovectores: definiciones y propiedades

 

Un ejemplo introductorio

Consideremos la matriz: \[A = \left( {\begin{array}{*{20}{c}}3&2\\1&4\end{array}} \right)\] Queremos ver cuál es el efecto que provoca esa matriz por los vectores de \({\mathbb{R}^2}\). ¿Qué pasa cuando uno multiplica esa matriz A por un vector? \[A.\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = \left( {\begin{array}{*{20}{c}}3&2\\1&4\end{array}} \right).\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{3x + 2y}\\{x + 4y}\end{array}} \right)\] Pensemos para que sea sencillo que tomamos el cuadrado con vértice en el origen de lado 1 y que está en el primer cuadrante: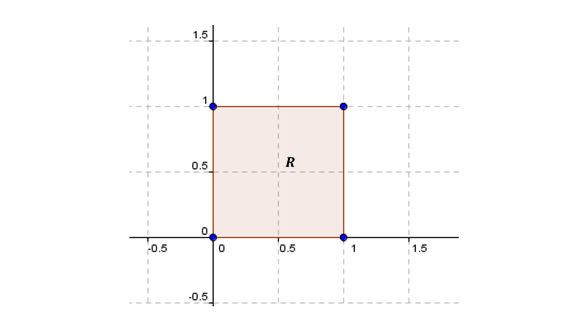

 

Digamos que llamamos a esta zona el recinto \(R\). ¿En qué se transformaría este recinto bajo el efecto de esa matriz? Para responder esta pregunta podemos ver en que se transforman sus vértices. Sabemos que el vector nulo se va a transformar en el vector nulo. Los demás serán: \[A\left( {\begin{array}{*{20}{c}}1\\0\end{array}} \right) = \left( {\begin{array}{*{20}{c}}3\\1\end{array}} \right)\] \[A\left( {\begin{array}{*{20}{c}}0\\1\end{array}} \right) = \left( {\begin{array}{*{20}{c}}2\\4\end{array}} \right)\] \[A\left( {\begin{array}{*{20}{c}}1\\1\end{array}} \right) = \left( {\begin{array}{*{20}{c}}5\\5\end{array}} \right)\]

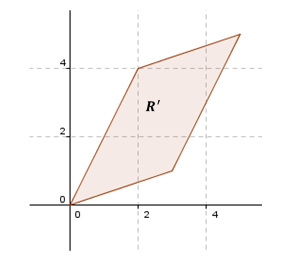
Uno se podría hacer esta pregunta: ¿Habrá vectores que después de la deformación conservan la dirección?

• El vector (1,0) se transformó en el (3,1). No conserva la dirección.
• El (0,1) se transforma en el (2,4). No conserva la dirección.
• El (1,1) se transformó el (5,5). Entonces se produjo una dilatación de factor 5, y se conservó la dirección.

Ese vector que mantuvo su dirección se denomina autovector, y el factor por el cual se dilató es el autovalor correspondiente.

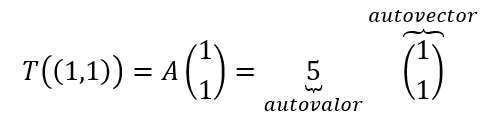
Autovalores, autovectores, autoespacios

Definición de autovalores y autovectores de una matriz

Sea \(A \in {\mathbb{R}^{n \times n}}\), \(\lambda \in \mathbb{R}\) es autovalor de \(A\) si y sólo si existe un vector \(v \in {\mathbb{R}^{n \times 1}}\) no nulo tal que: \[A.v = \lambda .v\;\;,\;\;v \ne {0_V}\] \(v\) se llama autovector asociado a \(\lambda \).

En el ejemplo que vimos recién el transformado de \(\left( {1,1} \right)\) es \(\left( {5,5} \right)\), entonces:

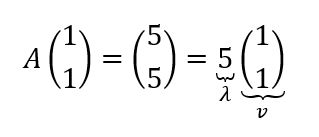
Veamos cómo hallar los autovalores y autovectores: Según la definición, debe cumplirse esta condición: \[Av = \lambda v\;\;{\rm{\;con\;}}v \ne {0_V}\] Restamos a ambos miembros \(\lambda v\): \[Av – \lambda v = {0_V}\] Premultiplicamos a \(v\) por \(I\), esto lo podemos hacer porque \(Iv = v\): \[Av – \lambda Iv = {0_V}\]

Entonces:

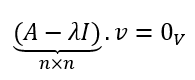
Resulta un sistema homogéneo con \(n\) ecuaciones y \(n\) incógnitas, donde \(A – \lambda I\) es la matriz de los coeficientes.

¿Cómo puede ser un sistema homogéneo en cuanto a su compatibilidad?

Respuesta: siempre compatible, porque siempre tiene la solución trivial. ¿Cómo queremos que sea en nuestro problema si estamos buscando vectores que no cambien su dirección? ¿Sistema compatible determinado (SCD) o sistema compatible indeterminado (SCI)?. Si es SCD, tiene únicamente la solución trivial y \(v\) es el vector nulo. Nuestro objetivo es obtener los autovectores (que son distintos del vector nulo), por eso necesitamos que este sistema sea compatible indeterminado.

Entonces: buscamos un sistema compatible indeterminado.

En un sistema cuadrado y homogéneo, el determinante decide: si es distinto de cero, tiene solución única. Entonces queremos que sea igual a cero:

\[\det \left( {A – \lambda I} \right) = 0\]

Esta es la ecuación característica de la matriz \(A\).

Y \(p\left( \lambda \right) = {\rm{det}}\left( {A – \lambda I} \right)\) es un polinomio de grado \(n\) dependiente de \(\lambda \) que se llama polinomio característico de la matriz \(A\).

Las raíces del polinomio característico son los autovalores de \(A\).

Una vez hallados los autovalores, ¿cómo obtenemos los autovectores?

Volvemos a la expresión original.

Para cada \(\lambda \) resolvemos el sistema:

\[\left( {A – \lambda I} \right).v = {0_V}\]

Y hallamos los autovectores correspondientes.

Si la matriz es de 2 por 2, el polinomio quedará de grado 2.

Si la matriz es de 3 por 3, el polinomio quedará de grado 3.

Otros nombre que se les suele dar a los autovectores y autovalores son:

• Valores propios y vectores propios
• Eigenvalores y Eigenvectores (Usando la raíz alemana eigen)

Ejemplo 1

Volvamos al ejemplo inicial. \[A – \lambda .I = \left( {\begin{array}{*{20}{c}}3&2\\1&4\end{array}} \right) – \lambda .\left( {\begin{array}{*{20}{c}}1&0\\0&1\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{3 – \lambda }&2\\1&{4 – \lambda }\end{array}} \right)\] \[\det \left( {A – \lambda I} \right) = 0\] \[\left( {3 – \lambda } \right)\left( {4 – \lambda } \right) – 2 = 0\] \[{\lambda ^2} – 7\lambda + 10 = 0\] \[{\lambda _1} = 2 \wedge {\lambda _2} = 5\] Para \(\lambda = 2\) resolvemos el sistema de ecuaciones: \[\left( {A – 2I} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\0\end{array}} \right)\] \[\left( {\begin{array}{*{20}{c}}1&2\\1&2\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\0\end{array}} \right)\] \[\left\{ {\begin{array}{*{20}{c}}{x + 2y = 0}\\{x + 2y = 0}\end{array}\; \Rightarrow x = – 2y} \right.\] La solución de un sistema homogéneo es siempre un subespacio. Los subespacios de autovectores se denominan autoespacios.

Buscamos una base de este subespacio: \[{S_2} = gen\left\{ {\left( {\begin{array}{*{20}{c}}2\\{ – 1}\end{array}} \right)} \right\}\] Éste es el subespacio donde están los autovectores asociados al autovalor 2. Para \(\lambda = 5\) \[\left( {A – 5I} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\0\end{array}} \right)\] \[\left( {\begin{array}{*{20}{c}}{ – 2}&2\\1&{ – 1}\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\0\end{array}} \right)\] \[\left\{ {\begin{array}{*{20}{c}}{ – 2x + 2y = 0}\\{x – y = 0}\end{array}\; \Rightarrow x = y} \right.\] \[{S_5} = gen\left\{ {\left( {\begin{array}{*{20}{c}}1\\1\end{array}} \right)} \right\}\] Resultado esperado porque habíamos visto que el \(\left( {1,1} \right)\) se transformaba en el \(\left( {5,5} \right)\).

Ejemplo 2

Consideremos la siguiente matriz de \(3 \times 3\): \[B = \left( {\begin{array}{*{20}{c}}3&2&{ – 1}\\2&3&1\\0&0&5\end{array}} \right)\] Busquemos sus autovalores resolviendo el polinomio característico: \[\left| {\begin{array}{*{20}{c}}{3 – \lambda }&2&{ – 1}\\2&{3 – \lambda }&1\\0&0&{5 – \lambda }\end{array}} \right| = 0\] \[\left( {5 – \lambda } \right).\left( {{{\left( {3 – \lambda } \right)}^2} – 4} \right) = 0\] Luego los autovalores son: \[{\lambda _1} = 5\;\; \vee \;\;\;{\lambda _2} = 5\;\; \vee \;\;{\lambda _3} = 1\] Donde la multiplicidad algebraica de \(5\) es 2. Esto significa que 5 es raíz doble del polinomio característico.

Para cada autovalor debemos resolver el sistema de ecuaciones \[\left( {\begin{array}{*{20}{c}}{3 – \lambda }&2&{ – 1}\\2&{3 – \lambda }&1\\0&0&{5 – \lambda }\end{array}} \right).\left( {\begin{array}{*{20}{c}}x\\{\begin{array}{*{20}{c}}y\\z\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}0\\0\end{array}}\end{array}} \right)\] Para obtener cuales son los autoespacios correspondientes a cada autovalor.

Autovectores asociados a \({\rm{\lambda }} = 5\):

Resolvamos el sistema compatible indeterminado: \[\left( {\begin{array}{*{20}{c}}{ – 2}&2&{ – 1}\\2&{ – 2}&1\\0&0&0\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\{\begin{array}{*{20}{c}}y\\z\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}0\\0\end{array}}\end{array}} \right) \Rightarrow \left\{ {\begin{array}{*{20}{c}}{ – 2x + 2y – z = 0}\\{2x – 2y + z = 0}\\{0 = 0}\end{array}} \right. \Rightarrow – 2x + 2y – z = 0\]

El subespacio asociado a este autovalor es: \[{S_5} = gen\left\{ {\left( {\begin{array}{*{20}{c}}1\\{\begin{array}{*{20}{c}}0\\{ – 2}\end{array}}\end{array}} \right),\left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}1\\2\end{array}}\end{array}} \right)} \right\}\;\]

Luego dos autovectores son: \[{v_1} = \left( {\begin{array}{*{20}{c}}1\\{\begin{array}{*{20}{c}}0\\{ – 2}\end{array}}\end{array}} \right)\;\;;\;\;\;{v_2} = \left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}1\\2\end{array}}\end{array}} \right)\]

Autovectores asociados a \({\rm{\lambda }} = 1\):

Resolvamos el sistema compatible indeterminado: \[\left( {\begin{array}{*{20}{c}}2&2&{ – 1}\\2&2&1\\0&0&4\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\{\begin{array}{*{20}{c}}y\\z\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}0\\0\end{array}}\end{array}} \right) \Rightarrow \left\{ {\begin{array}{*{20}{c}}{2x + 2y – z = 0}\\{2x + 2y + z = 0}\\{4z = 0}\end{array}} \right. \Rightarrow z = 0 \wedge y = – x\]

El subespacio asociado a este autovalor es: \[{S_1} = gen\left\{ {\left( {\begin{array}{*{20}{c}}1\\{\begin{array}{*{20}{c}}{ – 1}\\0\end{array}}\end{array}} \right)} \right\}\;\]

Luego un autovector es: \[{v_3} = \left( {\begin{array}{*{20}{c}}1\\{\begin{array}{*{20}{c}}{ – 1}\\0\end{array}}\end{array}} \right)\]

Finalmente hemos obtenido tres autovectores: \[{v_1} = \left( {\begin{array}{*{20}{c}}1\\{\begin{array}{*{20}{c}}0\\{ – 2}\end{array}}\end{array}} \right)\;\;;\;\;\;{v_2} = \left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}1\\2\end{array}}\end{array}} \right)\;\;{v_3} = \left( {\begin{array}{*{20}{c}}1\\{\begin{array}{*{20}{c}}{ – 1}\\0\end{array}}\end{array}} \right)\]

Donde \({v_1}\) y \({v_2}\) son autovectores asociados al autovalor \(\lambda = 5\) y \({v_3}\) es un autovalor asociado a \(\lambda = 1\).

Ejemplo 3

Consideremos la siguiente matriz de \(2 \times 2\): \[C = \left( {\begin{array}{*{20}{c}}0&{ – 2}\\2&0\end{array}} \right)\] Busquemos sus autovalores resolviendo el polinomio característico: \[\left| {\begin{array}{*{20}{c}}{ – \lambda }&{ – 2}\\2&{ – \lambda }\end{array}} \right| = 0\] \[ \Rightarrow \;{\lambda ^2} + 4 = 0\] Este polinomio no tiene raíces reales. Con lo cual diremos que \(C\) no tiene autovalores reales. Más adelante estudiaremos los números complejos y podremos hallar las raíces (complejas) del polinomio característico de C.

Ejemplo 4

Demuestre la siguiente propiedad para \(A \in {\mathbb{R}^{n \times n}}\)

\(\lambda = 0\) es autovalor de \(A \Leftrightarrow A\) no es inversible

Resolución

¿Cómo se demuestra esto? Primero veamos un ejemplo para convencernos de que se cumple la propiedad. Consideremos una matriz que no tenga inversa. Por ejemplo escribimos una matriz tal que la fila 2 sea el doble de la fila 1: \[A = \left( {\begin{array}{*{20}{c}}1&2\\2&4\end{array}} \right)\] Escribamos la ecuación característica y hallemos los autovalores: \[{p_A}\left( \lambda \right) = \left( {1 – \lambda } \right)\left( {4 – \lambda } \right) – 4 = 0\] \[{\lambda ^2} – 5\lambda = 0\; \Rightarrow \lambda = 0 \vee \lambda = 5\] En este caso particular hemos visto que una matriz no inversible tiene autovalor \(\lambda = 0\). Pero quisiéramos demostrar la propiedad. Para demostrar esto hay que recordar que:

\({\rm{\lambda }}\) es autovalor de \({\rm{A}}\) \( \Leftrightarrow \) \(\det \left( {{\rm{A}} – {\rm{\lambda I}}} \right) = 0\)

Pero si \(\lambda = 0\) entonces la afirmación queda:

 

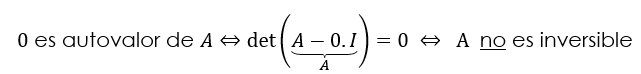
Ejercicio para el lector 1

Sea: \[A = \left( {\begin{array}{*{20}{c}}a&b\\c&d\end{array}} \right)\] Con autovalores \({\lambda _1}\) y \({\lambda _2}\) (iguales o distintos). Demostrar que: \[{\lambda _1} + {\lambda _2} = Traza\left( A \right)\] \[{\lambda _1}.{\lambda _2} = \det \left( A \right)\] Esta propiedad se generaliza para matrices de orden \(n\). Si \({\lambda _1},{\lambda _2}, \ldots ,{\lambda _n}\) son autovalores de \(A\) (iguales o distintos) entonces: \[{\lambda _1} + {\lambda _2} + \ldots + {\lambda _n} = Traza\left( A \right)\] \[{\lambda _1}.{\lambda _2}. \ldots .{\lambda _n} = \det \left( A \right)\]

Propiedad de los autovalores y autovectores

Los autovectores asociados a autovalores distintos son linealmente independientes. Demostración para dos autovalores Supongamos que tengo dos autovalores distintos: \({\lambda _1} \ne {\lambda _2}\). Como son autovalores, se cumple: \[A.{v_1} = {\lambda _1}.{v_1}\] \[A.{v_2} = {\lambda _2}.{v_2}\] Queremos probar que \({v_1}\) y \({v_2}\) son linealmente independientes. Veamos que la única combinación lineal de los vectores que da por resultado el vector nulo es la trivial (todos los coeficientes iguales a cero): \[\;{\alpha _1}.{v_1} + {\alpha _2}.{v_2} = {0_V}\;\;\;\;\;\;\;\;\;\;\;\;\;\left( 1 \right)\] Multiplicamos por \(A\) ambos miembros: \[A\left( {{\alpha _1}.{v_1} + {\alpha _2}.{v_2}} \right) = {0_V}\] Distribuimos: \[{\alpha _1}.A{v_1} + {\alpha _2}.A{v_2} = {0_V}\] Como \({v_1}\) y \({v_2}\) son autovectores es posible escribir: \[{\alpha _1}.{\lambda _1}{v_1} + {\alpha _2}.{\lambda _2}{v_2} = {0_V}\;\;\;\;\;\;\left( 2 \right)\] Ahora multipliquemos los dos miembros de la ecuación \(\left( 1 \right)\) por \({\lambda _1}\) : \[{\alpha _1}{\lambda _1}.{v_1} + {\alpha _2}.{\lambda _1}{v_2} = {0_V}\;\;\;\;\;\;\;\left( 3 \right)\] Y restando \(\left( 2 \right) – \left( 3 \right)\) obtenemos: Como \({\lambda _1} \ne {\lambda _2}\;\) por hipótesis entonces su diferencia no puede ser nula. Como \({v_2}\) es un autovector, no puede ser el vector nulo. Entonces: \[{\alpha _2} = 0\] Pero para demostrar que son linealmente independientes, nos falta ver que \({\alpha _1} = 0\). Sabiendo que \({\alpha _2} = 0\) vamos a \(\left( 1 \right)\): \[{\alpha _1}.{v_1} = {0_V} \Rightarrow {\alpha _1} = 0\] Y si \({\alpha _1} = {\alpha _2} = 0\) demostramos que \(\left\{ {{v_1},{v_2}} \right\}\) es linealmente independiente. O sea los autovectores que están en autoespacios diferentes son linealmente independientes.

Definición de autoespacio

Si \(\lambda \) es un autovalor de \(A\), se denomina autoespacio \({S_\lambda }\) al subespacio que contiene todos los autovectores asociados al autovalor \(\lambda \) y además el vector nulo. \[{S_\lambda } = \left\{ {v \in {\mathbb{R}^{n \times 1}}|\;Av = \lambda v} \right\} = \left\{ {v \in {\mathbb{R}^{n \times 1}}|\left( {A – \lambda I} \right)v = {0_V}} \right\}\]

Ejercicio para el lector 2

Sea \(A = \left( {{A_1}\;\;\;{A_2}\;\;\;{A_3}} \right) \in {\mathbb{R}^{3 \times 3}}\) con: \[{A_1} = \left( {\begin{array}{*{20}{c}}1\\{\begin{array}{*{20}{c}}2\\3\end{array}}\end{array}} \right)\;\;\;\;{\rm{y\;\;\;\;\;}}{{\rm{A}}_2} = \left( {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}1\\1\end{array}}\\0\end{array}} \right)\]

a) Hallar \({A_3}\) para que \(v = \left( {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}0\\1\end{array}}\\{ – 1}\end{array}} \right)\) sea autovector de \(A\) asociado a \(\lambda = 2\).

b) Hallar los restantes autovalores y autoespacios de \(A\).

Videos relacionados con Autovalores y Autovectores