Determinante de una matriz

Introducción

Vimos previamente que no todas las matrices son inversibles.

¿Cómo podemos saber si una matriz tiene inversa?

El determinante de una matriz proporciona información para responder a esta pregunta.

Cuando vimos producto vectorial y mixto, habíamos definido determinantes de orden 2 y de orden 3. Recordamos aquí las fórmulas presentadas:

A cada matriz cuadrada puede asignársele un número real que llamaremos su determinante y designaremos como \(det\left( A \right)\) o \(\left| A \right|\) .

Para matrices \(2×2\) y \(3×3\) el determinante se calcula como sigue:

\[A = \left( {\begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}\\{{a_{21}}}&{{a_{22}}}\end{array}} \right)\;\;\; \Rightarrow \;\;\;\left| A \right| = \left| {\begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}\\{{a_{21}}}&{{a_{22}}}\end{array}} \right| = {a_{11}}\;{a_{22}} – {a_{12}}\;{a_{21}}\] \[A = \left( {\begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\{{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\{{a_{31}}}&{{a_{32}}}&{{a_{33}}}\end{array}} \right)\;\;\; \Rightarrow \;\;\;\left| A \right| = {a_{11}}\;\left| {\begin{array}{*{20}{c}}{{a_{22}}}&{{a_{23}}}\\{{a_{32}}}&{{a_{33}}}\end{array}} \right|\; – \;{a_{12}}\;\left| {\begin{array}{*{20}{c}}{{a_{21}}}&{{a_{23}}}\\{{a_{31}}}&{{a_{33}}}\end{array}} \right|\; + \;{a_{13}}\;\left| {\begin{array}{*{20}{c}}{{a_{21}}}&{{a_{22}}}\\{{a_{31}}}&{{a_{32}}}\end{array}} \right|\]

Observación: El determinante no está definido para matrices rectangulares.

Ejemplo

El determinante de \(A = \left( {\begin{array}{*{20}{c}}3&{ – 1}&{ – 1}\\2&1&0\\3&1&2\end{array}} \right)\) es: \[\det \left( A \right) = 3.\left| {\begin{array}{*{20}{c}}1&0\\1&2\end{array}} \right| – \left( { – 1} \right).\left| {\begin{array}{*{20}{c}}2&0\\3&2\end{array}} \right| + \left( { – 1} \right).\left| {\begin{array}{*{20}{c}}2&1\\3&1\end{array}} \right|\] \[\det \left( A \right) = 3.2 – \left( { – 1} \right).4 + \left( { – 1} \right).\left( { – 1} \right)\] \[\;\;\det \left( A \right) = 11\]

La regla de Sarrus es una forma práctica de calcular determinantes, sólo aplicable para matrices de \(3 \times 3\).

Consideremos el siguiente esquema en el cual agregamos al final de una matriz de \(3 \times 3\) las filas 1 y 2. El determinante se calcula sumando los productos indicados por las flechas que que van de izquierda a derecha y restando los productos indicados por las flechas que van de derecha a izquierda:

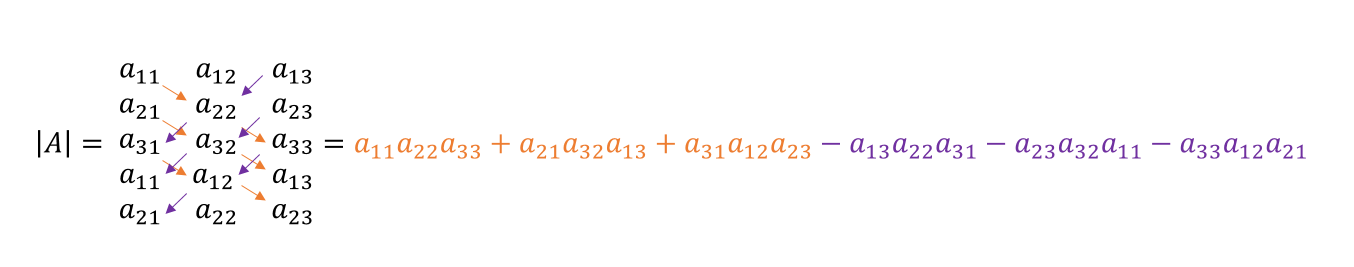
Para la matriz considerada en el ejemplo anterior:

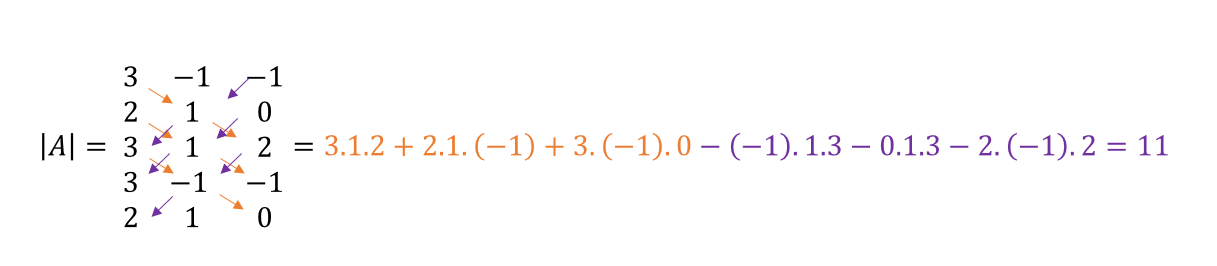
Desarrollo de un determinante por cofactores

Dada \(A \in {\mathbb{R}^{nxn}}\), se denomina menor \({M_{ij}}\) a la submatriz de \(\left( {n – 1} \right) \times \;\left( {n – 1} \right)\) que se obtiene a partir de \(A\) eliminando la fila \(i\) y la columna \(j\).

Se denomina cofactor \({C_{ij}}\) del elemento \({a_{ij}}\) al producto de \({\left( { – 1} \right)^{i + j}}\) por el determinante de la matriz menor \({M_{ij}}\;\):

\[{C_{ij}} = {\left( { – 1} \right)^{i + j}}\det \left( {{M_{ij}}} \right)\]

Por ejemplo para la matriz

\[A = \left( {\begin{array}{*{20}{c}}3&1&4\\{ – 1}&2&1\\3&2&1\end{array}} \right)\]

Las matrices menores y los cofactores de la primera fila son:

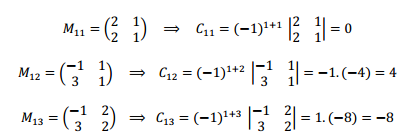
Observación: \[{\left( { – 1} \right)^{i + j}} = \left\{ {\begin{array}{*{20}{c}}{1\;\;\;\;si\;\;i + j\;\;\;es\;\;par}\\{ – 1\;\;\;\;si\;\;i + j\;\;\;es\;\;impar}\end{array}} \right.\] Con estas definiciones previas, estamos en condiciones de enunciar el desarrollo de un determinante de orden \(n\).

El determinante de una matriz puede calcularse utilizando los cofactores de cualquier fila o cualquier columna.

Desarrollo por fila \(i\):

\[\det \left( A \right) = {a_{i1}}{C_{i1}} + {a_{i2}}{C_{i2}} + \ldots + {a_{in}}{C_{in}} = \mathop \sum \limits_{j = 1}^n {a_{ij}}\;{C_{ij}}\] Este cálculo se puede hacer tomando cualquiera de las filas de \(A\), o sea: \(i = 1,\;2,\; \ldots ,\;n\)

Desarrollo por columna \(j\):

\[\det \left( A \right) = {a_{1j}}{C_{1j}} + {a_{2j}}{C_{2j}} + \ldots + {a_{nj}}{C_{nj}} = \mathop \sum \limits_{i = 1}^n {a_{ij}}\;{C_{ij}}\;\;\;,\;\;\;\;j = 1,\;2, \ldots ,n\]

Ejemplo

Retomemos la matriz del ejemplo anterior: \[A = \left( {\begin{array}{*{20}{c}}3&1&4\\{ – 1}&2&1\\3&2&1\end{array}} \right)\] El desarrollo del determinante por fila 1 es: \[\det \left( A \right) = {a_{11}}\;{C_{11}} + {a_{12}}\;{C_{12}} + {a_{13}}\;{C_{13}}\] Reemplazando los cofactores calculados previamente, resulta: \[\det \left( A \right) = 3.0 + 1.4 + 4.\left( { – 8} \right) = – 28\] Veamos que si desarrollamos el determinante por la columna 3 obtenemos el mismo resultado: \[\det \left( A \right) = {a_{13}}\;{C_{13}} + {a_{23}}\;{C_{23}} + {a_{33}}\;{C_{33}}\] \[{C_{13}} = {\left( { – 1} \right)^{1 + 3}}\left| {\begin{array}{*{20}{c}}{ – 1}&2\\3&2\end{array}} \right| = – 8\] \[{C_{23}} = {\left( { – 1} \right)^{2 + 3}}\;\left| {\begin{array}{*{20}{c}}3&1\\3&2\end{array}} \right| = – 3\] \[{C_{33}} = {\left( { – 1} \right)^{3 + 3}}\;\left| {\begin{array}{*{20}{c}}3&1\\{ – 1}&2\end{array}} \right| = 7\] \[\det \left( A \right) = 4.\left( { – 8} \right) + 1.\left( { – 3} \right) + 1.7 = – 28\] El lector puede comprobar que el determinante no varía si se desarrolla por otra fila o columna.

Ejemplo

Calculemos el determinante de la siguiente matriz: \[A = \left( {\begin{array}{*{20}{c}}2&1&0&{ – 1}\\0&{ – 1}&0&3\\{ – 2}&1&1&{ – 2}\\3&2&0&1\end{array}} \right)\]

Observemos que resulta económico desarrollar el determinante por la tercera columna:

Calculemos el cofactor \({C_{33}}\): \[{C_{33}} = {\left( { – 1} \right)^{3 + 3}}\left| {\begin{array}{*{20}{c}}2&1&{ – 1}\\0&{ – 1}&3\\3&2&1\end{array}} \right|\] Para el cálculo del determinante de esta matriz de \(3 \times 3\) es conveniente usar la primera columna: \[{C_{33}} = 2.{\left( { – 1} \right)^{1 + 1}}\left| {\begin{array}{*{20}{c}}{ – 1}&3\\2&1\end{array}} \right| + 3.{\left( { – 1} \right)^{3 + 1}}\left| {\begin{array}{*{20}{c}}1&{ – 1}\\{ – 1}&3\end{array}} \right|\] \[{C_{33}} = – 14 + 6 = – 8\] Este ejemplo muestra que para simplificar los cálculos, en general es conveniente desarrollar el determinante por la fila o columna que tenga mayor cantidad de ceros.

Determinante de una matiz triangular

Si \(A \in {\mathbb{R}^{3 \times 3}}\) es triangular: \[A = \left( {\begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\0&{{a_{22}}}&{{a_{23}}}\\0&0&{{a_{33}}}\end{array}} \right)\]

¿Cuál es la expresión de su determinante?

Podemos calcular el determinante de \(A\) por la primera columna:

\[\det \left( A \right) = {a_{11}}\left| {\begin{array}{*{20}{c}}{{a_{22}}}&{{a_{23}}}\\0&{{a_{33}}}\end{array}} \right| = {a_{11}}{a_{22}}{a_{33}}\]

Hemos llegado a la siguiente conclusión: si \(A \in {\mathbb{R}^{3 \times 3}}\) es triangular, su determinante es el producto de los elementos de la diagonal principal.

Esto se puede generalizar para matrices de cualquier orden: si \(A \in {\mathbb{R}^{n \times n}}\) es triangular, su determinante es el producto de los elementos de la diagonal principal.

\(A \in {\mathbb{R}^{n \times n}}\) triangular \( \Rightarrow \det \left( A \right) = {a_{11}}.{a_{22}} \ldots {a_{nn}}\)

Teniendo en cuenta que la matriz identidad es triangular, se deduce que:

\[det(I)=1\]

Propiedades de los determinantes

En general (es decir, a menos que la matriz sea triangular o tenga alguna otra cualidad especial), el cálculo de determinantes por medio del desarrollo por cofactores no es eficiente por el número de operaciones que implica cuando se trabaja con matrices grandes.

A continuación veremos una serie de propiedades que facilitan el cálculo de determinantes.

Sea \(A \in {\mathbb{R}^{n \times n}}\). En lo que sigue utilizaremos la notación:

\[A = \left( {{A_1}\;\;{A_2}\;\; \ldots \;\;\;{A_n}} \right)\]

donde \({A_j}\) representa la columna \(j\) de la matriz \(A\).

Propiedad 1

Como un determinante puede desarrollarse por cofactores tomando cualquier fila o columna de la matriz, se deduce que:

Por lo tanto, todas las propiedades que enunciemos para las columnas de una matriz son válidas para sus filas.

Propiedad 2

Si \(B\) es la matriz que se obtiene multiplicando una columna de A por un escalar \(k \in \mathbb{R}\), \(det\left( B \right)\; = \;k\;det\left( A \right)\). O sea:

Comprobemos la propiedad para una matriz de \(2 \times 2\): \[A = \left( {\begin{array}{*{20}{c}}a&b\\c&d\end{array}} \right)\;\;\;,\;\;\;\det \left( A \right) = ad – bc\] \[\det \left( {\begin{array}{*{20}{c}}a&{kb}\\c&{kd}\end{array}} \right) = akd – kbc = k\left( {ad – bc} \right) = k\det \left( A \right)\]

Propiedad 3

Si una columna de \(A\) puede expresarse como $$A_{j}=A_{j}^{‘}+A_{j}^{»}$$ entonces \(det\left( A \right)\) puede descomponerse así:

Comprobemos para una matriz de \(2 \times 2\):

\[\det \left( {\begin{array}{*{20}{c}}a&{b’ + b»}\\c&{d’ + d»}\end{array}} \right) = a\left( {d’ + d»} \right) – c\left( {b’ + b»} \right)\]

\[ = ad’ + ad» – cb’ – cb» = \left( {ad’ – cb’} \right) + \left( {ad» – cb»} \right)\]

\[ = \det \left( {\begin{array}{*{20}{c}}a&{b’}\\c&{d’}\end{array}} \right) + \det \left( {\begin{array}{*{20}{c}}a&{b»}\\c&{d»}\end{array}} \right)\]

Propiedad 4

Si se permutan dos columnas de A, el determinante cambia de signo:

Comprobemos para una matriz de \(2 \times 2\): \[\left| {\begin{array}{*{20}{c}}b&a\\d&c\end{array}} \right| = bc – ad = – \left( {ad – bc} \right) = – \left| {\begin{array}{*{20}{c}}a&b\\c&d\end{array}} \right|{\rm{\;}}\]

Propiedad 5

Si \(A\) tiene una columna \(0\) de ceros, entonces su determinante es cero:

Esta propiedad puede deducirse aplicando la propiedad 2: \[\det \left( {{A_1}\; \ldots 0 \ldots \;\;{A_n}} \right) = \det \left( {{A_1}\; \ldots \;0{A_j}\; \ldots \;\;{A_n}} \right) = 0\det \left( {{A_1}\; \ldots \;{A_j}\; \ldots \;\;{A_n}} \right) = 0\]

Propiedad 6

Si A tiene dos columnas iguales, entonces su determinante es cero:

Esta propiedad puede deducirse de la propiedad 4 cuando se permutan las columnas iguales.

Propiedad 7

Si \(\;\;{A_j} = k\;{A_i}\;\;\left( {k \in \mathbb{R}} \right)\), entonces el determinante es cero:

Dejamos la demostración a cargo del lector.

Propiedad 8

Si a una columna se le suma un múltiplo de otra, el determinante no varía. La demostración se basa en algunas de las propiedades anteriores:

La demostración se basa en las propiedades 3 y 7 enunciadas previamente.

Propiedad 9

Si \(A \in {\mathbb{R}^{\color{red}{n}x\color{red}{n}}}\) y \(k \in \mathbb{R}\):

Proponemos al lector que demuestre esta propiedad, teniendo en cuenta la propiedad 2.

Propiedad 10

El determinante de un producto de matrices cuadradas es igual al producto de sus determinantes. Si \(A,B \in {\mathbb{R}^{n \times n}}\) , entonces:

Observación importante: el determinante de la suma de matrices no es igual a la suma de sus determinantes.

Veamos un ejemplo: \[A = \left( {\begin{array}{*{20}{c}}1&2\\3&4\end{array}} \right)\;\;,\;\;\;B = \left( {\begin{array}{*{20}{c}}1&{ – 1}\\3&2\end{array}} \right)\] \[A + B = \left( {\begin{array}{*{20}{c}}2&1\\6&6\end{array}} \right)\] \(\det \left( {\rm{A}} \right) = – 2{\rm{\;\;\;\;}},{\rm{\;\;\;}}\det \left( {\rm{B}} \right) = 5\) pero \(\det \left( {A + B} \right) = 6\; \ne – 2 + 5\)

Entonces:

\(\det \left( {A + B} \right) \ne \det \left( A \right) + \det \left( B \right)\)

Propiedad 11

Si \(k \in \mathbb{N}\), teniendo en cuenta la propiedad anterior se deduce que:

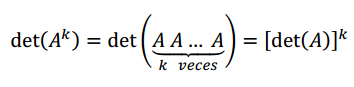
Ejemplo

Sea la matriz \[A = \left( {\begin{array}{*{20}{c}}1&2&3\\2&3&{ – 1}\\2&4&6\end{array}} \right)\] Calcular el determinante de \({A^{100}}\)

Resolución

Obtener \({A^{100}}\) resulta complicado por la cantidad de cálculos que implica.

Podemos usar la propiedad 11 para simplificar los cálculos:

\[\det \left( {{A^{100}}} \right) = {\left[ {\det \left( A \right)} \right]^{100}}\] Y como \({F_3} = 2{F_{1\;}}\), de la propiedad 7 se deduce que \(\det \left( A \right) = 0\) .

Luego: \[\det \left( {{A^{100}}} \right) = 0\]

Ejemplo

Calculemos el determinante de la matriz \[A = \left( {\begin{array}{*{20}{c}}{ – 3}&2&2&{ – 3}\\2&0&2&2\\1&{ – 1}&{ – 1}&1\\1&0&1&1\end{array}} \right)\] Como \({A_1} = {A_4}\) podemos afirmar que \(\det \left( A \right) = 0\)  (propiedad 6).

Ejemplo

Calculemos el determinante de la matriz

\[A = \left( {\begin{array}{*{20}{c}}1&{ – 2}&{ – 1}&{ – 1}\\2&3&{ – 2}&5\\0&1&{ – 3}&1\\1&1&0&2\end{array}} \right)\]

Si tenemos en cuenta que \({A_4} = {A_1} + {A_2}\;\), aplicando propiedades podemos afirmar que \(\det \left( A \right) = 0\) . ¿Por qué?

Ejemplo

Sea \(A \in {\mathbb{R}^{3 \times 3}}\) y \(\det \left( A \right) = 2\), calcular \(\det \left( {\frac{3}{2}\;{A^3}} \right)\)

Resolución

\[\det \left( {\frac{3}{2}\;{A^3}} \right) = {\left( {\frac{3}{2}} \right)^3}\det \left( {{A^3}} \right) = \frac{{27}}{8}\;{[\det \left( A \right)]^3} = \frac{{27}}{8}{.2^3} = 27\] Donde usamos las propiedades 9 y 11.

Ejemplo

Queremos calcular el determinante de la siguiente matriz de \(4 \times 4\):

\[A = \left( {\begin{array}{*{20}{c}}1&2&3&4\\1&1&0&1\\2&1&3&{ – 1}\\3&1&3&0\end{array}} \right)\]

Aplicamos la propiedad 8 para obtener ceros en la primera columna:

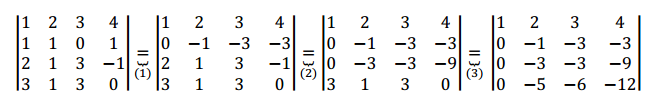
Donde hemos realizado: \[\left( 1 \right):\;\;\;{F_2} \to {F_2} – {F_1}\] \[\left( 2 \right):\;\;\;{F_3} \to {F_3} – 2{F_1}\] \[\left( 3 \right):\;{F_4} \to {F_4} – 3{F_1}\] Ahora podemos desarrollar el determinante por la primera columna:

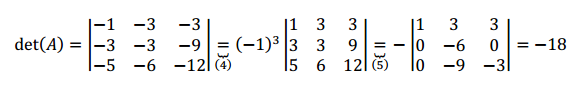
\[\left( 4 \right):Propiedad\;9\;de\;determinantes\;\] \[\left( 5 \right):{F_2} \to {F_2} – 3{F_1}\;\;{\rm{y}}\;\;{F_3} \to {F_3} – 5{F_1}\;\] Observemos que la aplicación de la propiedad 8 nos permitió reducir el cálculo de un determinante de \(4 \times 4\) a uno de \(3 \times 3\).

Ejercicio para el lector 5

Sea \(\;A \in {\mathbb{R}^{3 \times 3}}\), \(A\; = \;\left( {{A_1}\;\;{A_2}\;\;{A_3}} \right)\)

Demostrar la siguiente propiedad:

Si \(\;\;{A_3} = {\alpha _1}{A_1} + {\alpha _2}{A_2}\;\;\;,\;\;\;{\alpha _1},{\alpha _2} \in \mathbb{R}\) entonces el determinante de \(A\) es cero.

El determinante de la inversa

Recordemos que una matriz \(A \in {\mathbb{R}^{nxn}}\) es inversible si existe \(B \in {\mathbb{R}^{nxn}}\) tal que \(AB = I\) . Si \(A\) es inversible, su inversa se indica como \({A^{ – 1}}\) y se verifica que: \[A\;{A^{ – 1}} = I\] Aplicando determinantes, resulta: \[\det \left( {A\;{A^{ – 1}}} \right) = \det \left( I \right) = 1\] Como el determinante es distributivo respecto del producto: \[\det \left( A \right)\;\det \left( {{A^{ – 1}}} \right) = 1\]
Entonces:

Para que esta fórmula sea válida, el determinante de A debe ser distinto de cero. Por lo tanto, el determinante permite decidir si una matriz tiene inversa:

Por ejemplo \(M = \left( {\begin{array}{*{20}{c}}3&1\\0&1\end{array}} \right)\) es inversible porque \(\det \left( M \right) \ne 0\) .

En cambio \(\;A = \left( {\begin{array}{*{20}{c}}3&1\\{ – 3}&{ – 1}\end{array}} \right)\) no es inversible porque \(\det \left( A \right) = 0\) .

Observación:

Las matrices inversibles también se llaman regulares.

Las matrices no inversibles también se denominan singulares.

Ejemplo

Sea \(A = \left( {{A_1}\;\;\;{A_2}\;\;{A_3}} \right) \in {\mathbb{R}^{3 \times 3}}\) , \(\det \left( A \right) = k \ne 0\)

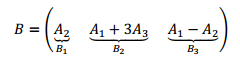
Mostrar que \(B\) es inversible y calcular \(\det \left( { – 2{A^t}{B^{ – 1}}} \right)\)

Resolución

\[\;B\;es\;inversible \Leftrightarrow \det \left( B \right) \ne 0\] \[\det \left( {\rm{B}} \right) = \det \left( {{A_2}\;\;\;\;\;{A_1} + 3{A_3}\;\;\;\;{A_1} – {A_2}} \right)\] Usando la propiedad 3:

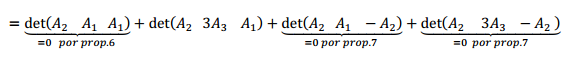
Luego utilizando propiedades 2 y 4:

\(\det \left( {\rm{B}} \right) = \det \left( {{A_2}\;\;3{A_3}\;\;{A_1}} \right)\)

\( = 3.\det \left( {{A_2}\;\;{A_3}\;\;{A_1}} \right)\)

\( = 3.\left( {–1} \right).\det \left( {{A_1}\;\;{A_3}\;\;{A_2}} \right)\)

\( = 3.{\left( {–1} \right)^2}.\det \left( {{A_1}\;\;{A_2}\;\;{A_3}} \right)\)

\( = 3k\)

Cómo \(k \ne 0\), \(B\) es inversible y el determinante de su inversa es:

\[\det \left( {{B^{ – 1}}} \right) = \frac{1}{{{\rm{det}}\left( B \right)}} = \frac{1}{{3k}}\]

Luego:

\[det\left( {–2{A^t}{B^{–1}}} \right) = {\left( {–2} \right)^3}det\left( {{A^t}} \right)det\left( {{B^{–1}}} \right) = –8.k.\frac{1}{{3k}} = –\frac{8}{3}\]

Ejercicio para el lector 6

Utilizar wxMaxima para calcular el determinante, en función de \(k\), de la siguiente matriz: \[A = \left( {\begin{array}{*{20}{c}}1&3&1&3\\2&3&4&5\\3&2&k&2\\4&k&6&5\end{array}} \right)\] Determinar los valores de \(k\) para los cuales la matriz es inversible.

Sugerencia: para resolver este ejercicio pueden ser útiles los comandos para calcular el determinante, simplificar una expresión algebraica y hallar las raíces de un polinomio que se explican en el tutorial de wxMaxima.

Matriz Adjunta

Dada una matriz \(A \in {\mathbb{R}^{nxn}}\), se denomina matriz de cofactores de \(A\) a la matriz que se obtiene reemplazando cada elemento de \(A\) por su respectivo cofactor.

Por ejemplo para una matriz de \(3 \times 3\), su matriz de cofactores es: \[Cof\left( A \right) = \left( {\begin{array}{*{20}{c}}{{C_{11}}}&{{C_{12}}}&{{C_{13}}}\\{{C_{21}}}&{{C_{22}}}&{{C_{23}}}\\{{C_{31}}}&{{C_{32}}}&{{C_{33}}}\end{array}} \right)\] La traspuesta de la matriz de cofactores se denomina adjunta de \(A\) y se indica como \(Adj\left( A \right)\): \[Adj\left( A \right) = {\left( {Cof\left( A \right)} \right)^t} = \left( {\begin{array}{*{20}{c}}{{C_{11}}}&{{C_{21}}}&{{C_{31}}}\\{{C_{12}}}&{{C_{22}}}&{{C_{32}}}\\{{C_{13}}}&{{C_{23}}}&{{C_{33}}}\end{array}} \right)\]

Ejemplo

Dada \(A = \left( {\begin{array}{*{20}{c}}1&2&3\\4&5&6\\7&8&0\end{array}} \right){\rm{\;}}\), calculemos sus cofactores para obtener la matriz adjunta: \[\;{C_{11}} = {\left( { – 1} \right)^{1 + 1}}\left| {\begin{array}{*{20}{c}}5&6\\8&0\end{array}} \right| = – 48\;\;\;\;\;\;\;\;\;\;{C_{12}} = {\left( { – 1} \right)^{1 + 2}}\left| {\begin{array}{*{20}{c}}4&6\\7&0\end{array}} \right| = 42\;\;\;\;\;\;\;\;{C_{13}} = {\left( { – 1} \right)^{1 + 3}}\left| {\begin{array}{*{20}{c}}4&5\\7&8\end{array}} \right| = – 3\] \[{C_{21}} = {\left( { – 1} \right)^{2 + 1}}\left| {\begin{array}{*{20}{c}}2&3\\8&0\end{array}} \right| = 24\;\;\;\;\;\;\;{C_{22}} = {\left( { – 1} \right)^{2 + 2}}\left| {\begin{array}{*{20}{c}}1&3\\7&0\end{array}} \right| = – 21\;\;\;\;\;\;\;{C_{23}} = {\left( { – 1} \right)^{2 + 3}}\left| {\begin{array}{*{20}{c}}1&2\\7&8\end{array}} \right| = 6\] \[{C_{31}} = {\left( { – 1} \right)^{3 + 1}}\left| {\begin{array}{*{20}{c}}2&3\\5&6\end{array}} \right| = – 3\;\;\;\;\;\;{C_{32}} = {\left( { – 1} \right)^{3 + 2}}\left| {\begin{array}{*{20}{c}}1&3\\4&6\end{array}} \right| = 6\;\;\;\;\;{C_{33}} = {\left( { – 1} \right)^{3 + 3}}\left| {\begin{array}{*{20}{c}}1&2\\4&5\end{array}} \right| = – 3\] Observación: Recordemos que \({\left( { – 1} \right)^{i + j}} = \left\{ {\begin{array}{*{20}{c}}{1\;\;\;\;si\;\;i + j\;\;\;es\;\;par}\\{ – 1\;\;\;\;si\;\;i + j\;\;\;es\;\;impar}\end{array}} \right.\)

Esto facilita el cálculo de los cofactores, ya que \({\left( { – 1} \right)^{i + j}}\) indica un signo \( + \) o \( – \) de acuerdo con la posición de cada elemento \({a_{ij}}\).

Entonces la matriz de los cofactores es:

\[Cof\left( A \right) = \left( {\begin{array}{*{20}{c}}{ – 48}&{42}&{ – 3}\\{24}&{ – 21}&6\\{ – 3}&6&{ – 3}\end{array}} \right)\]

Trasponemos para obtener la adjunta:

\[Adj\left( A \right) = \left( {\begin{array}{*{20}{c}}{ – 48}&{24}&{ – 3}\\{42}&{ – 21}&6\\{ – 3}&6&{ – 3}\end{array}} \right)\]

Si \(A\) es inversible, veremos que su adjunta proporciona un método para obtener la inversa.

Obtención de la inversa a través de la adjunta

Habíamos visto que el determinante permite decidir si una matriz es inversible.

El lector puede comprobar para la matriz del ejemplo anterior que:

\(\det \left( A \right) = 27 \Rightarrow A\) es inversible

Calculemos el producto de la matriz \(A\) con su adjunta:

\[A\;Adj\left( A \right) = \left( {\begin{array}{*{20}{c}}1&2&3\\4&5&6\\7&8&0\end{array}} \right)\left( {\begin{array}{*{20}{c}}{ – 48}&{24}&{ – 3}\\{42}&{ – 21}&6\\{ – 3}&6&{ – 3}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{27}&0&0\\0&{27}&0\\0&0&{27}\end{array}} \right)\]

¿Y si lo calculamos invirtiendo el orden? En general el producto de matrices no es conmutativo, pero en este caso:

\[Adj\left( A \right)\;A = \left( {\begin{array}{*{20}{c}}{ – 48}&{24}&{ – 3}\\{42}&{ – 21}&6\\{ – 3}&6&{ – 3}\end{array}} \right).\left( {\begin{array}{*{20}{c}}1&2&3\\4&5&6\\7&8&0\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{27}&0&0\\0&{27}&0\\0&0&{27}\end{array}} \right)\]

Se cumple que el producto de la matriz por su adjunta (en cualquier orden) da por resultado una matriz escalar que tiene en su diagonal al determinante de la matriz \(A\). Esto no es casual sino que se cumple para toda matriz cuadrada.

Si \(A \in {\mathbb{R}^{nxn}}\) , puede demostrarse que:

De esta propiedad puede deducirse que:

\[A\left( {\;\frac{1}{{{\rm{det}}\left( A \right)}}\;Adj\left( A \right)} \right) = I\;\;\;\;\;\; \wedge \;\;\;\;\;\;\;\;\;\left( {\;\frac{1}{{{\rm{det}}\left( A \right)}}\;Adj\left( A \right)} \right)A = I\;\]

Por lo tanto podemos afirmar que \(si\;\;{\bf{det}}\left( A \right) \ne 0\) , la inversa de \(A\) es:

Retomando el ejemplo anterior, \[{A^{ – 1}} = \frac{1}{{27}}\;\left( {\begin{array}{*{20}{c}}{ – 48}&{24}&{ – 3}\\{42}&{ – 21}&6\\{ – 3}&6&{ – 3}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{ – \frac{{16}}{9}}&{\frac{8}{9}}&{ – \frac{1}{9}}\\{\frac{{14}}{9}}&{ – \frac{7}{9}}&{\frac{2}{9}}\\{ – \frac{1}{9}}&{\frac{2}{9}}&{ – \frac{1}{9}}\end{array}} \right)\]

Caso particular: inversa de una matriz de 2×2

Sea \(A = \left( {\begin{array}{*{20}{c}}a&b\\c&d\end{array}} \right)\)

Si \(\det \left( A \right) = ad – bc \ne 0\) , podemos afirmar que A es inversible y calcular su inversa mediante la matriz adjunta.

Dejamos a cargo del lector comprobar que la matriz adjunta es: \[Adj\left( A \right) = \left( {\begin{array}{*{20}{c}}d&{ – b}\\{ – c}&a\end{array}} \right)\]
Y por lo tanto, resulta:

Por ejemplo, para

\(A = \left( {\begin{array}{*{20}{c}}1&2\\3&4\end{array}} \right)\;\;,\;\;la\;inversa\;es\;\;\;\;\;{A^{ – 1}} = – \frac{1}{2}\;\left( {\begin{array}{*{20}{c}}4&{ – 2}\\{ – 3}&1\end{array}} \right)\; = \;\left( {\begin{array}{*{20}{c}}{ – 2}&1\\{3/2}&{ – 1/2}\end{array}} \right)\)