Enunciado del Segundo Parcial de Álgebra [10-06-2017]
El siguiente es el enunciado y resolución completa del segundo parcial de álgebra y geometría analítica tomado el día 10-06-2017, en el curso semi-presencial.

Resolución del Segundo parcial de Álgebra [10-06-2017]
Ejercicio 1
Dada la transformación lineal \(T:{\mathbb{R}^3} \to {\mathbb{R}^2}\;\;|\;\;T\left( {x,y,z} \right) = \left( {x + kz,x + \left( {2 – k} \right)y + kz} \right)\), halle todos los valores de \(k\) para que la imagen de \(T\) tenga dimensión \(2\).
Resolución del ejercicio 1
Si los vectores de la imagen de T son \(\left( {x + kz,x + \left( {2 – k} \right)y + kz} \right)\) entonces podemos re-escribirlos separando \(x\), \(y\) y \(z\) de la siguiente forma:
\[\left( {x + kz,x + \left( {2 – k} \right)y + kz} \right)\]
\[ = \left( {x,x} \right) + \left( {0,\left( {2 – k} \right)y} \right) + \left( {kz,kz} \right)\]
\[ = x\left( {1,1} \right) + y\left( {0,2 – k} \right) + z\left( {k,k} \right)\]
Dónde \(x,y,z \in \mathbb{R}\).
Entonces la imagen está generada por:
\[Im\left( T \right) = gen\left\{ {\left( {1,1} \right),\left( {0,2 – k} \right),\left( {k,k} \right)} \right\}\]
Tenemos que analizar qué pasa con la dimensión de \(Im\left( T \right)\) cuando:
- \(k = 0\)
- \({\rm{k}} = 2\)
- \({\rm{k}} \ne 0 \wedge k \ne 2\)
Si \(k = 0\) la dimensión de la imagen es 2:
\[Im\left( T \right) = gen\left\{ {\left( {1,1} \right),\left( {0,2} \right),\left( {0,0} \right)} \right\}\]
\[ \Rightarrow {B_{Im\left( T \right)}} = \left\{ {\left( {1,1} \right),\left( {0,2} \right)} \right\}\]
\[ \Rightarrow \dim \left( {Im\left( T \right)} \right) = 2\]
Si \(k = 2\) la dimensión de la imagen es 1:
\[Im\left( T \right) = gen\left\{ {\left( {1,1} \right),\left( {0,0} \right),\left( {2,2} \right)} \right\}\]
\[ \Rightarrow {B_{Im\left( T \right)}} = \left\{ {\left( {1,1} \right)} \right\}\]
\[ \Rightarrow \dim \left( {Im\left( T \right)} \right) = 1\]
Si \(k \ne 0 \wedge k \ne 2\) entonces la dimensión de la imagen es 2:
\(Im\left( T \right) = gen\left\{ {\left( {1,1} \right),\left( {0,2 – k} \right),\left( {k,k} \right)} \right\}{\rm{\;}}\) con \({\rm{\;}}k \ne 0 \wedge k \ne 2\)
Dónde los vectores \({v_1}\) y \({v_2}\) son LI, pero \({v_3}\) es LD con \({v_1}\).
Entonces:
\( \Rightarrow {B_{Im\left( T \right)}} = \left\{ {\left( {1,1} \right),\left( {0,2 – k} \right)} \right\}{\rm{\;\;\;}}\)con \({\rm{\;}}k \ne 0 \wedge k \ne 2\)
\[ \Rightarrow \dim \left( {Im\left( T \right)} \right) = 2\]
Luego \(k \in \mathbb{R} – \left\{ 2 \right\}\)
OTRA FORMA DE PENSARLO:
La transformación lineal \(T\) tiene asociada una matriz estándar que se puede obtener transformando a los vectores de la base canónica de \({\mathbb{R}^3}\) y poniendo cómo columnas a sus imágenes:
\[T\left( {1,0,0} \right) = \left( {1,1} \right)\]
\[T\left( {0,1,0} \right) = \left( {0,2 – k} \right)\]
\[T\left( {0,0,1} \right) = \left( {k,k} \right)\]
\[ \Rightarrow M\left( T \right) = \left( {\begin{array}{*{20}{c}}1&0&k\\1&{2 – k}&k\end{array}} \right)\]
El rango de la matriz asociada es igual a la dimensión de la imagen.
Entonces para que la imagen de \(T\) sea de dimensión 2, debe ser el rango de \(M\left( T \right)\) igual a \(2\).
Si \(k = 2\) la matriz tiene rango \(1\).
Para todo otro valor de \(k\) la matriz tiene rango \(2\).
Luego \(k \in \mathbb{R} – \left\{ 2 \right\}\)
Ejercicio 2
¿Verdadero o falso? Justifique sus respuestas.
a) Toda transformación lineal \(T:{P_2} \to {\mathbb{R}^2}\) no puede ser biyectiva.
b) Si \(B \in {\mathbb{R}^{3 \times 3}}\) tiene polinomio característico \(p\left( \lambda \right) = – {\left( {\lambda + 3} \right)^2}\left( {\lambda – 1} \right)\),
\(S = \left\{ {\left( {\begin{array}{*{20}{c}}x\\{\begin{array}{*{20}{c}}y\\z\end{array}}\end{array}} \right) \in {\mathbb{R}^{3 \times 1}}\;|\;x + z = 0} \right\}\) es un autoespacio de \(B\) y el otro autoespacio asociado tiene dimensión \(1\), entonces \(B\) es diagonalizable.
Resolución del ejercicio 2
Ítem a
Verdadero.
Consideremos que: \(\dim \left( {{P_2}} \right) = 3\) y que \(\dim \left( {{\mathbb{R}^2}} \right) = 2\).
Por el teorema de las dimensiones se cumple que:
\[\dim \left( {{P_2}} \right) = \dim \left( {Nu} \right) + \dim \left( {Im} \right)\]
¿Qué valores pueden tomar las dimensiones del núcleo y la imagen?
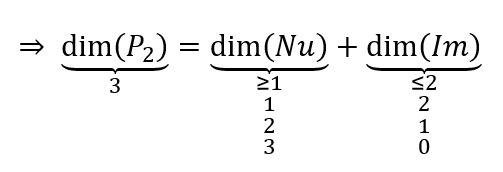
Cómo la dimensión del núcleo debe ser mayor o igual a 1, entonces la función no puede ser inyectiva… y no puede ser bieyctiva tampoco.
Ítem b
Verdadero.
Conociendo que el polinomio característico es \(p\left( \lambda \right) = – {\left( {\lambda + 3} \right)^2}\left( {\lambda – 1} \right)\), sabemos que los autovalores son:
\(\lambda = – 3{\rm{\;}}\left( {doble} \right){\rm{\;}},{\rm{\;\;}}\lambda = 1{\rm{\;}}\left( {simple} \right)\)
Los autoespacios son:
\[S = \left\{ {\left( {\begin{array}{*{20}{c}}{\rm{x}}\\{\begin{array}{*{20}{c}}y\\z\end{array}}\end{array}} \right) \in {\mathbb{R}^{3 \times 1}}{\rm{\;}}|{\rm{\;}}x + z = 0} \right\} \Rightarrow {\rm{\;\;\;}}\dim \left( S \right) = 2\]
\[T{\rm{\;\;\;}}|{\rm{\;\;}}\dim \left( T \right) = 1\]
El autoespacio S debe ser el autoespacio asociado al autovalor de multiplicidad algebraica 2.
Porque la dimensión de los autoespacios debe estar comprendida entre 1 y la multiplicidad algebraica del autovalor: \(1 \le \dim \left( {{S_\lambda }} \right) \le {m_\lambda }\).
Luego es posible hallar tres autovectores \(LI\) (dos autovectores serán de \(S\) y otro autovector de \(T\)).
Entonces \(B\) es diagonalizable.
Ejercicio 3
Sea la transformación lineal \(F:{\mathbb{R}^3} \to {\mathbb{R}^{2 \times 1}}{\rm{\;}}|{\rm{\;}}M{\left( F \right)_{{B_1}{B_2}}} = {\rm{\;}}\left( {\begin{array}{*{20}{c}}0&1&1\\1&1&0\end{array}} \right)\) siendo \({B_1}\) base canónica de \({\mathbb{R}^3}\) y \({B_2} = \left\{ {\left( {\begin{array}{*{20}{c}}{ – 1}\\2\end{array}} \right),\left( {\begin{array}{*{20}{c}}0\\1\end{array}} \right)} \right\}\) base de \({\mathbb{R}^{2 \times 1}}\)
a) Halle todos los \(v \in {\mathbb{R}^3}\) para los cuales \(F\left( v \right) = \left( {\begin{array}{*{20}{c}}3\\{ – 9}\end{array}} \right)\)
b) Obtenga una base de \(Nu\left( F \right)\)
Resolución del ejercicio 3
Ítem a
La matriz asociada a la transformación lineal opera con las coordenadas de los vectores en ciertas bases \({B_1}\) y \({B_2}\). Recordemos que cumple la siguiente propiedad:
\[M{\left( F \right)_{{B_1}{B_2}}}.{\left[ v \right]_{{B_1}}} = {\left[ {F\left( v \right)} \right]_{{B_2}}}\]
Entonces busquemos las coordenadas de \(F\left( v \right)\) en \({B_2}\):
\[\alpha \left( {\begin{array}{*{20}{c}}{ – 1}\\2\end{array}} \right) + \beta \left( {\begin{array}{*{20}{c}}0\\1\end{array}} \right) = \left( {\begin{array}{*{20}{c}}3\\{ – 9}\end{array}} \right)\]
\[ \Rightarrow {\rm{\;\;}}\left\{ {\begin{array}{*{20}{c}}{ – \alpha = 3}\\{2\alpha + \beta = – 9}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{\alpha = – 3}\\{\beta = – 3}\end{array}} \right.\]
\[{\left[ {F\left( v \right)} \right]_{{B_2}}} = \left( {\begin{array}{*{20}{c}}{ – 3}\\{ – 3}\end{array}} \right)\]
Los vectores \(v = \left( {a,b,c} \right)\) que buscamos tienen coordenadas en la base canónica que coinciden con sus componentes:
\[{\left[ v \right]_{{B_1}}} = \left( {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}a\\b\end{array}}\\c\end{array}} \right)\]
Luego los vectores \(v = \left( {a,b,c} \right)\) que buscamos deben cumplir que:
\[\left( {\begin{array}{*{20}{c}}0&1&1\\1&1&0\end{array}} \right)\left( {\begin{array}{*{20}{c}}a\\{\begin{array}{*{20}{c}}b\\c\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{ – 3}\\{ – 3}\end{array}} \right)\]
Multiplicando e igualando obtenemos un sistema de dos ecuaciones con tres incógnitas:
\[\left( {\begin{array}{*{20}{c}}{b + c}\\{a + b}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{ – 3}\\{ – 3}\end{array}} \right)\]
\[ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{b + c = – 3}\\{a + b = – 3}\end{array}} \right.{\rm{\;}}\]
\[ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{c – a = 0}\\{a + b = – 3}\end{array}} \right.\]
\[ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{c = a}\\{b = – 3 – a}\end{array}} \right.\]
\[{\left[ v \right]_{{B_1}}} = \left( {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}a\\{ – 3 – a}\end{array}}\\a\end{array}} \right) \Rightarrow v = \left( {a, – 3 – a,a} \right)\]
Entonces los infinitos vectores \(v\) tales que \(F\left( v \right)\) es \(\left( {\begin{array}{*{20}{c}}3\\{ – 9}\end{array}} \right)\) son los de la siguiente recta:
\[ \Rightarrow v = a\left( {1, – 1,1} \right) + \left( {0, – 3,0} \right){\rm{\;\;\;}},{\rm{\;\;\;}}a \in \mathbb{R}\]
Ítem b
Los vectores del núcleo son los \(w = \left( {x,y,z} \right)\) tales que \(F\left( w \right) = \left( {\begin{array}{*{20}{c}}0\\0\end{array}} \right)\).
Entonces:
\[w = \left( {x,y,z} \right) \in Nu\left( F \right) \Leftrightarrow \left( {\begin{array}{*{20}{c}}0&1&1\\1&1&0\end{array}} \right)\left( {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}x\\y\end{array}}\\z\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\0\end{array}} \right)\]
Multiplicando e igualando obtenemos un sistema de dos ecuaciones con tres incógnitas:
\[ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{y + z = 0}\\{x + y = 0}\end{array}} \right.\]
\[ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{z = – y}\\{x = – y}\end{array}} \right.\]
Luego los vectores \(w\) del núcleo son de la forma:
\[w = \left( { – y,y, – y} \right) = y\left( { – 1,1, – 1} \right)\]
\[Nu\left( F \right) = \left\{ {\left( {x,y,z} \right) \in {\mathbb{R}^3}{\rm{\;}}|{\rm{\;}}x + y = 0 \wedge y + z = 0{\rm{\;}}} \right\}{\rm{\;}}\]
\[{B_{Nu\left( F \right)}} = \left\{ {\left( { – 1,1, – 1} \right)} \right\}\]
Ejercicio 4
Sea la superficie \(A{\left( {x – 2} \right)^2} + B{y^2} + C{\left( {z – 2} \right)^2} = 1\)
a) Halle \(A\), \(B\), \(C\) para que la superficie sea un hiperboloide de una hoja de eje paralelo al eje \(y\) y su traza con el plano \(xz\) sea una elipse de eje focal paralelo al eje \(x\) cuyos semiejes tengan longitud \(2\) y \(3\).
b) Para \(A = 1,\) \(B = C = – 1\) identifique y grafique la superficie.
Resolución
Ítem a
Para que sea un hiperboloide de una hoja, tiene que tener dos signos positivos y uno negativo.
Para que el eje del hiperboloide sea paralelo al eje y tiene que tener el signo negativo en el término con que tiene a \(y\). Entonces \(B<0\).
La traza con el plano \(\color{blue}{xz\left( {y = 0} \right)}\) debe ser una elipse de eje focal paralelo al eje x cuyos semiejes tienen longitud 2 y 3. Entonces debemos obtener una ecuación así:
\[\left\{ {\begin{array}{*{20}{c}}{ \color{green}{+} \frac{{{{\left( {x – 2} \right)}^2}}}{{{\color{red}{3^2}}}} \color{green}{+} \frac{{{{\left( {z – 2} \right)}^2}}}{{{\color{fuchsia}{2^2}}}} = 1}\\{\color{blue}{y = 0}}\end{array}} \right.{\rm{\;\;\;\;\;\;\;\;}}\left[ 1 \right]\]
Reemplazamos por \(y = 0\) en la ecuación y trabajamos la expresión para compararla con \(\left[ 1 \right]\):
\[\left\{ {\begin{array}{*{20}{c}}{A{{\left( {x – 2} \right)}^2} + B{y^2} + C{{\left( {z – 2} \right)}^2} = 1}\\{y = 0}\end{array}} \right.\]
\[ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{A{{\left( {x – 2} \right)}^2} + C{{\left( {z – 2} \right)}^2} = 1}\\{y = 0}\end{array}} \right.\]
\[ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{\frac{{{{\left( {x – 2} \right)}^2}}}{{\frac{1}{A}}} + \frac{{{{\left( {z – 2} \right)}^2}}}{{\frac{1}{C}}} = 1}\\{y = 0}\end{array}} \right.\]
Comparando con [1]:
\[ \Rightarrow \frac{1}{A} = {3^2} \wedge \frac{1}{C} = {2^2}\]
\[ \Rightarrow A = \frac{1}{9} \wedge C = \frac{1}{4}\]
Entonces debe ser \(A = 1/9\), \(B \in \left( { – \infty ,0} \right)\) y \(C = 1/4\).
Ítem b
Al reemplazar \(A = 1\), \(B = C = – 1\) obtenemos la siguiente ecuación:
\[{\rm{\;}} \color{blue}{+} {\left( {x – \color{red}{2}} \right)^2} \color{fuchsia}{-} {y^2} \color{fuchsia}{-} {\left( {z – \color{red}{2}} \right)^2} = 1\]
¿Qué características tiene esta ecuación?
- Las tres variables aparecen elevadas al cuadrado
- Hay dos coeficientes negativos y uno positivo
- Está igualada a 1
Entonces se trata de un hiperboloide de dos hojas con eje paralelo al eje \(\color{blue}{x}\), y centro en \(\color{red}{\left( {2,0,2} \right)}\).
A continuación, una gráfica del hiperboloide de dos hojas:
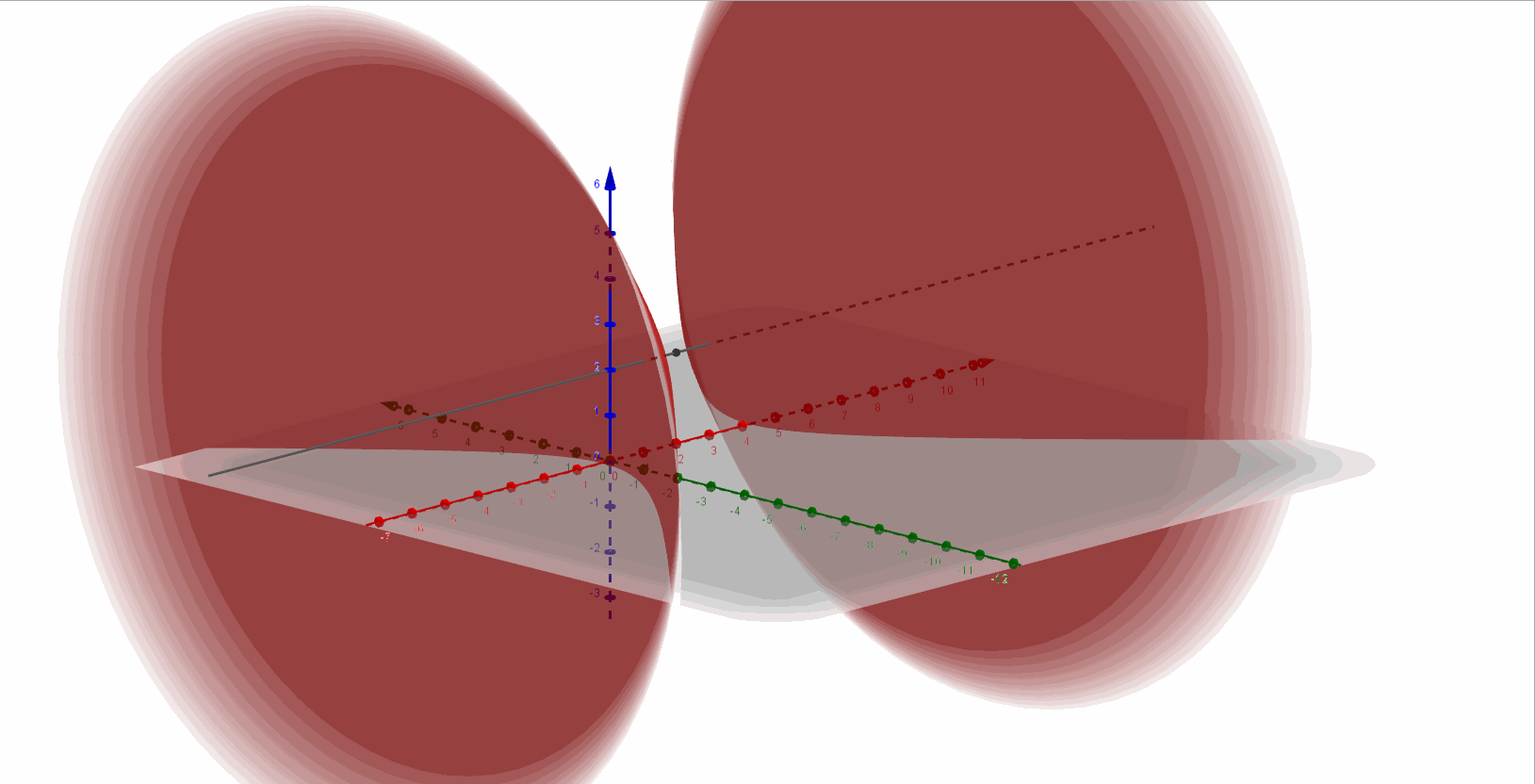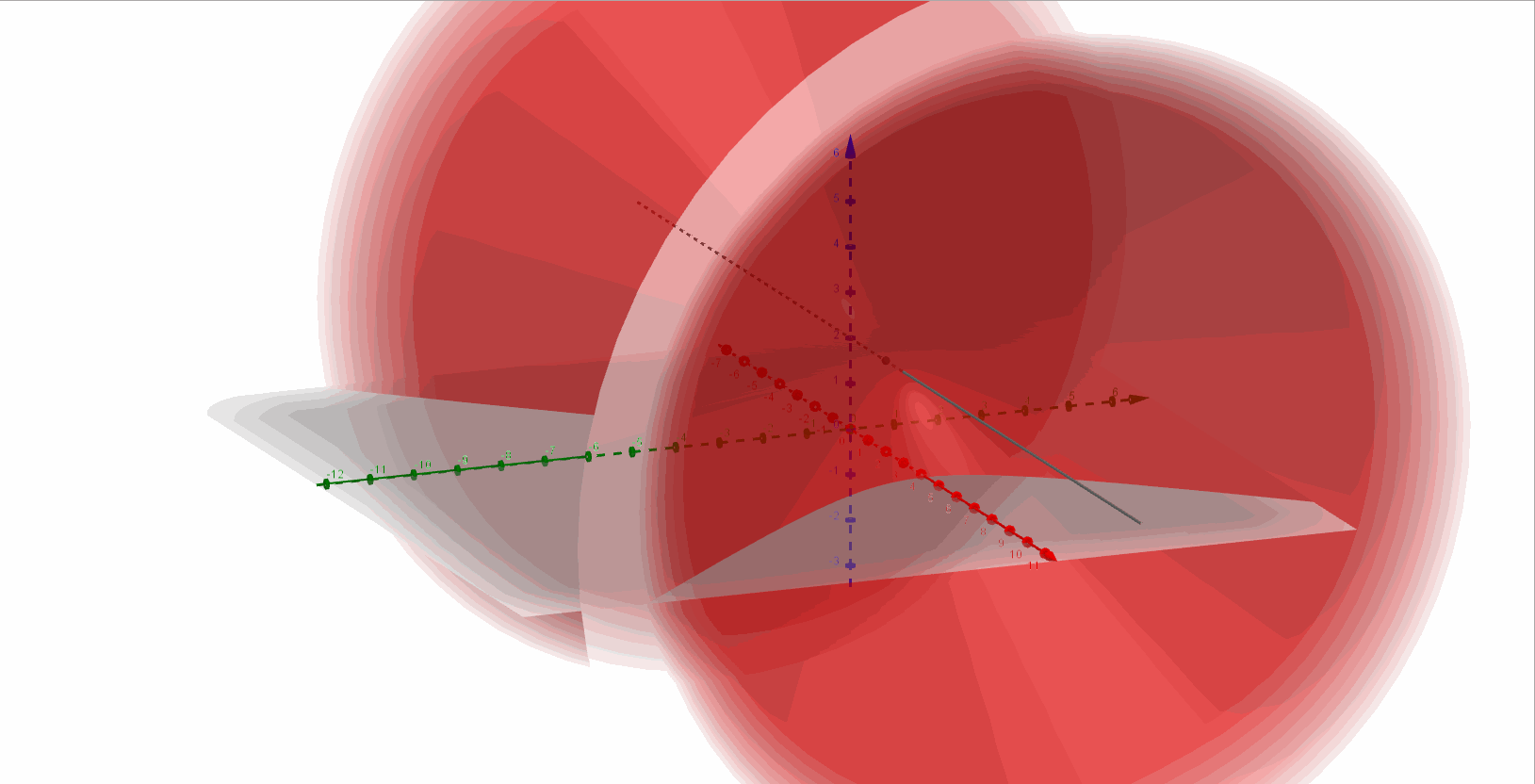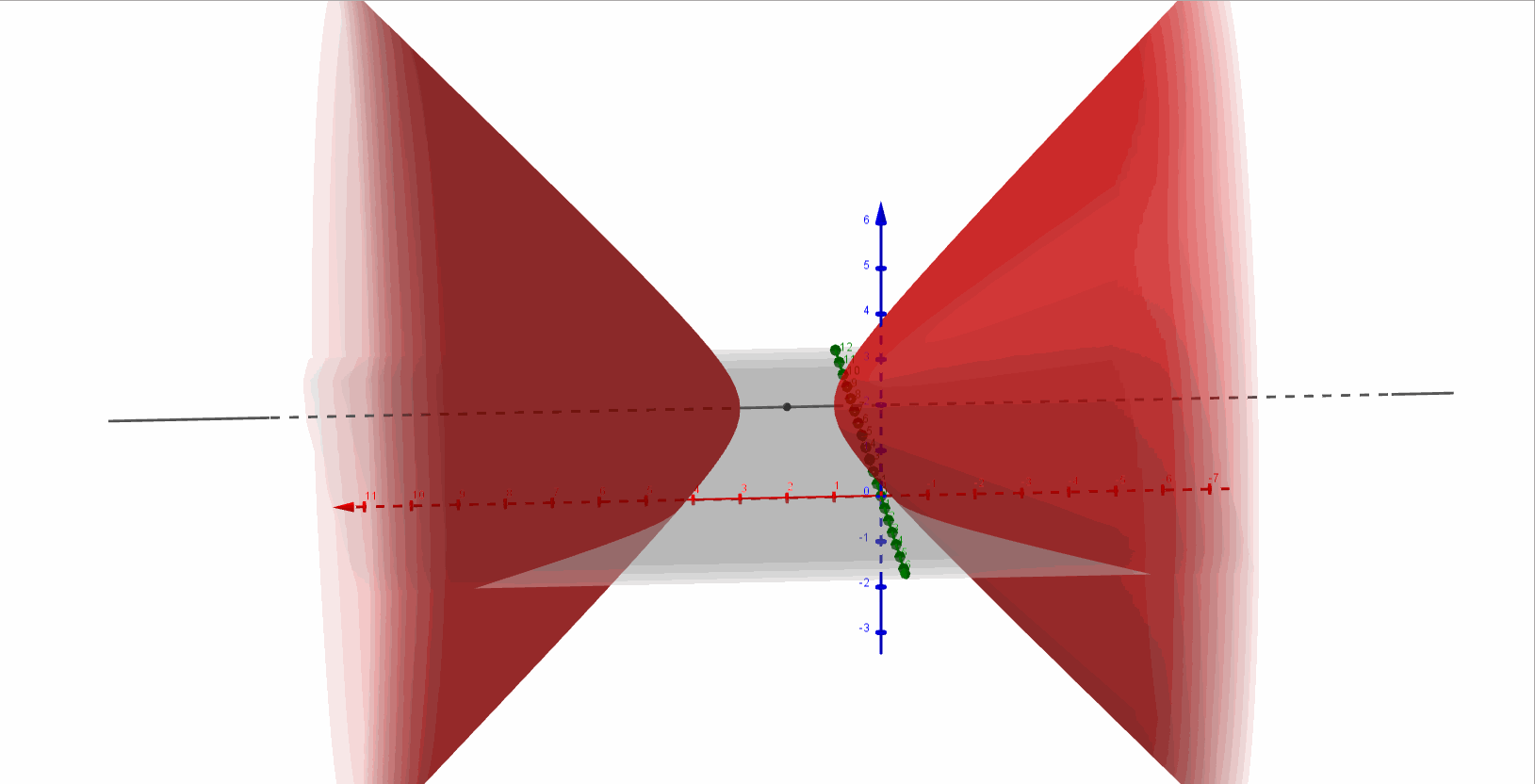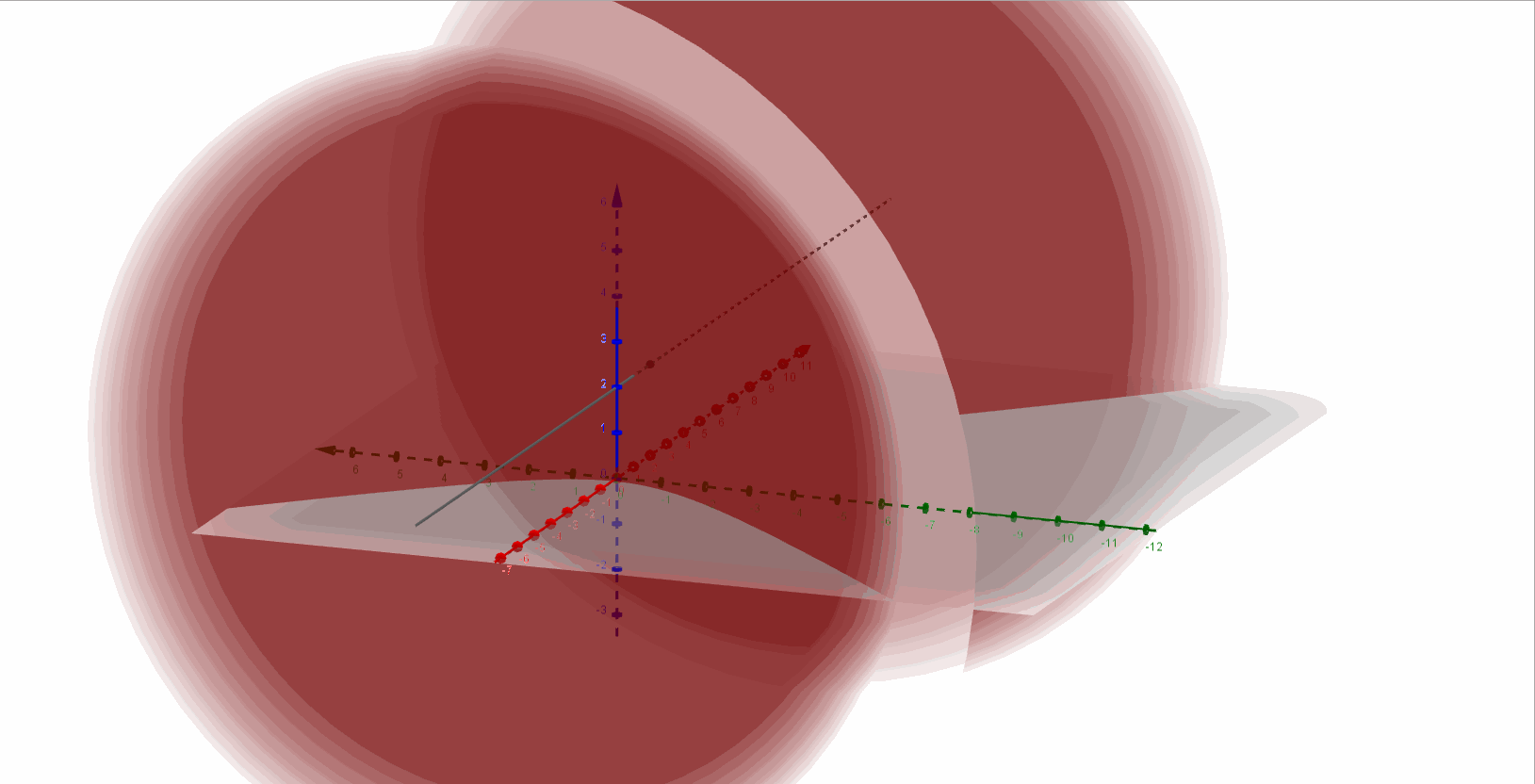
Ejercicio 5
Resolver la siguiente ecuación en \(\mathbb{C}\): \({x^4} + 27x = 0\)
Resolución del ejercicio 5
Sacamos factor común \(x\):
\[x\left( {{x^3} + 27} \right) = 0\]
Para que el producto sea igual a cero, alguno de los factores debe ser cero:
\[ \Rightarrow \;x = 0 \vee {x^3} = -27\]
Luego tenemos que calcular las raíces cúbicas de -27… en el conjunto de los números complejos (En los reales la única raíz cúbica de -27 es -3. Pero en los complejos hay exactamente tres raíces cúbicas de -27).
Usando la fórmula de radicación de complejos:
\[\sqrt[3]{{-27}} = \sqrt[3]{{\left| {-27} \right|}}.\left( {\cos \left( {\frac{{Arg\left( {-27} \right) + 2k\pi }}{3}} \right) + i.{\rm{sen}}\left( {\frac{{Arg\left( {-27} \right) + 2k\pi }}{3}} \right)} \right)\]
Para \(k=0,1,2\).
Hallemos módulo y argumento del número complejo \(-27\):
\[\left| {-27} \right| = 27\]
\[Arg\left( {-27} \right) = \pi\]
Entonces sus raíces son:
\[{x_k} = \sqrt[3]{{27}}.\left( {\cos \left( {\frac{{\pi + 2k\pi }}{3}} \right) + i.{\rm{sen}}\left( {\frac{{\pi + 2k\pi }}{3}} \right)} \right){\rm{\;\;\;}}k = 0,1,2\]
Con\({\rm{\;}}k = 0\):
\[{x_0} = \sqrt[3]{{27}}.\left( {\cos \left( {\frac{\pi }{3}} \right) + i.{\rm{sen}}\left( {\frac{\pi }{3}} \right)} \right) = 3\left( {\frac{1}{2} + i.\frac{{\sqrt 3 }}{2}} \right) = \color{red}{\frac{3}{2} + i\frac{{3\sqrt 3 }}{2}}\]
Con \(k = 1\):
\[{x_1} = \sqrt[3]{{27}}.\left( {\cos \left( {\frac{{\pi + 2\pi }}{3}} \right) + i.{\rm{sen}}\left( {\frac{{\pi + 2\pi }}{3}} \right)} \right) = 3\left( {–1 + i.0} \right) = \color{green}{- 3}\]
Con \(k = 2\):
\[{x_2} = \sqrt[3]{{27}}.\left( {\cos \left( {\frac{{\pi + 2.2.\pi }}{3}} \right) + i.{\rm{sen}}\left( {\frac{{{\rm{\pi }} + 2.2.\pi }}{3}} \right)} \right) = 3.\left( {\frac{1}{2}–\frac{{i\sqrt 3 }}{2}} \right) =\color{fuchsia}{ \frac{3}{2}–i.\frac{{3\sqrt 3 }}{2}}\]
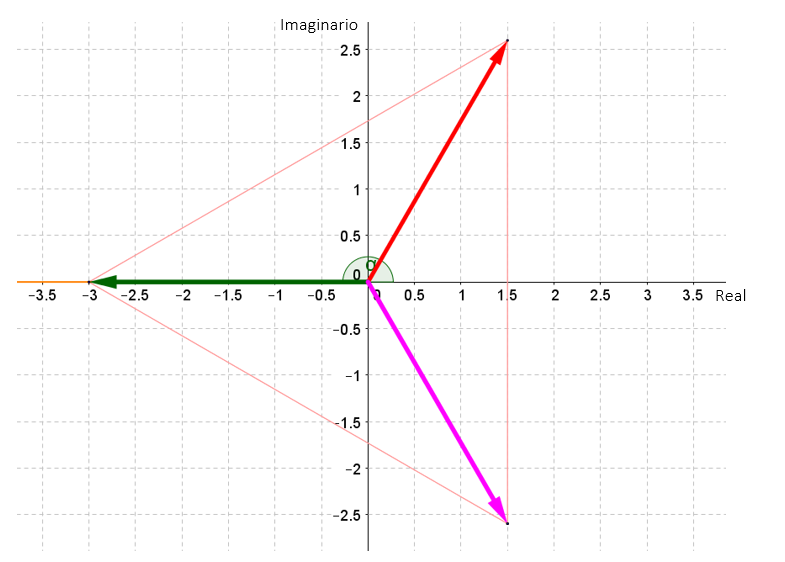
Finalmente podemos escribir el conjunto solución de la ecuación original:
\[S = \left\{ {0,\; – 3,\frac{3}{2} + i.\frac{{3\sqrt 3 }}{2},\frac{3}{2}–i.\frac{{3\sqrt 3 }}{2}} \right\}\]

