Ejemplos introductorios
Ejemplo 1
Sea \(T\) la siguiente transformación lineal: \[T:{\mathbb{R}^2} \to {\mathbb{R}^3}{\rm{\;}}|{\rm{\;\;}}T\left( {\left( {x,y} \right)} \right) = \left( {x + 2y,x – y,y} \right)\] ¿Existirá una matriz \(A\) que multiplicada por \(\left( {x,y} \right)\) dé por resultado \(\left( {x + 2y,x – y,y} \right)\)? Para esto vamos a escribir los vectores como columna: \[A.\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{x + 2y}\\{\begin{array}{*{20}{c}}{x – y}\\y\end{array}}\end{array}} \right)\]
¿Cuál debería ser el tamaño de la matriz?
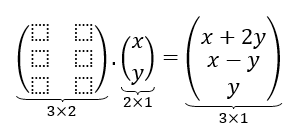
Efectuando el producto de matrices, podemos obtener los coeficientes de \(A\) :
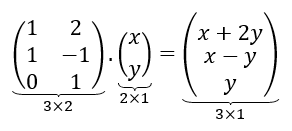
Encontramos una matriz que realiza la transformación lineal. Se conoce como la matriz estándar de la transformación lineal.
Notemos que la transformación va de \({\mathbb{R}^2}\) a \({\mathbb{R}^3}\), y que el orden de la matriz es \(3 \times 2\).
Ejemplo 2
Ahora consideremos la siguiente transformación lineal:
\[F:{\mathbb{R}^3} \to {\mathbb{R}^2}{\rm{\;}}|{\rm{\;}}F\left( {\left( {x,y,z} \right)} \right) = \left( {x + 2z, – y} \right)\]
Queremos buscar una matriz \(B\) tal que:
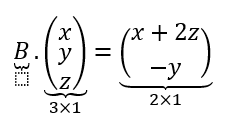
Pensando el orden de la matriz y el valor de sus elementos llegamos a:
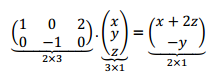
Hemos hallado de manera intuitiva la matriz estándar de la transformación lineal. Notemos que la transformación va de \({\mathbb{R}^3}\) a \({\mathbb{R}^2}\) y que el orden de la matriz asociada a la transformación lineal es \(2 \times 3\).
Construcción de la matriz asociada a una transformación lineal
Hemos visto ejemplos de cómo surge a partir del producto de matrices, la matriz estándar de una transformación lineal de \({\mathbb{R}^n}\) a \({\mathbb{R}^m}\). En lo que sigue intentaremos generalizar para cualquier espacio vectorial de dimensión finita, el concepto de matriz asociada a una transformación lineal. Aun en el caso de TL en \({\mathbb{R}^n}\), veremos que no siempre la matriz estándar es la más conveniente.
Sea \(T:V \to W\;\) transformación lineal, y
\[\dim \left( V \right) = n\] \[{\rm{\;dim}}\left( W \right) = m\] \[B = \left\{ {{v_1},{v_2}, \ldots ,{v_n}} \right\}{\rm{\;}}base{\rm{\;}}de{\rm{\;}}V\] \[B’ = \left\{ {{w_1}, \ldots ,{w_m}} \right\}{\rm{\;}}base{\rm{\;}}de{\rm{\;}}W\]
Designamos:
\(M{\left( T \right)_{BB’}}\) a la matriz asociada a la transformación lineal \(T\) respecto de las bases \(B\) y \(B’\).
Esta matriz se construye por columnas transformando los vectores de la base \(B\) (del dominio), y expresando los transformados en sus coordenadas en la base \(B’\):
La matriz asociada tiene \(n\) columnas porque la base \(B\) tiene \(n\) vectores, y tiene \(m\) filas porque las coordenadas en \(B’\) se escriben con \(m\) componentes. O sea que si \(dim\left( V \right){\rm{\;}} = {\rm{\;}}n\) y \(dim\left( W \right){\rm{\;}} = {\rm{\;}}m\), \(M{\left( T \right)_{BB’}} \in {\mathbb{R}^{m \times n}}\)
Propiedad
La matriz asociada a una transformación lineal cumple la siguiente propiedad:
Ejemplo 3
Retomemos la transformación lineal:
\[T:{\mathbb{R}^2} \to {\mathbb{R}^3}{\rm{\;}}|{\rm{\;\;}}T\left( {\left( {x,y} \right)} \right) = \left( {x + 2y,x – y,y} \right)\] Consideremos las siguientes bases para el dominio y codominio:
\[B = \left\{ {\left( {0,1} \right),\left( {1,1} \right)} \right\}{\rm{\;}}\] \[B’ = \left\{ {\left( {1,0,0} \right),\left( {1,1,0} \right),\left( {0,1,1} \right)} \right\}\]
Construyamos la matriz asociada a la transformación \(T\) de la base \(B\) a la base \(B’\), es decir \(M{\left( T \right)_{BB{\rm{‘}}}} \):
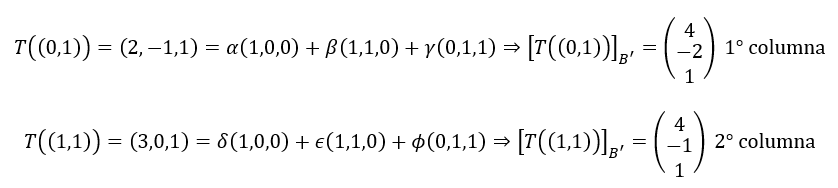
\[M{\left( T \right)_{BB{\rm{‘}}}} = \left( {\begin{array}{*{20}{c}}4&4\\{ – 2}&{ – 1}\\1&1\end{array}} \right)\]
Dado un vector cualquiera, aunque no conozcamos la fórmula, conociendo la matriz y las dos bases podemos calcular su transformado. Vamos a tomar un vector cualquiera de \({\mathbb{R}^2}\) y lo transformamos… sin mirar la fórmula. Hallemos \(T\left( {\left( {3,5} \right)} \right)\) mediante la matriz asociada \(M{\left( T \right)_{BB’}}\) : \[M{\left( T \right)_{BB{\rm{‘}}}}{\left[ v \right]_B} = {\left[ {T\left( v \right)} \right]_{B{\rm{‘}}}}\] No podemos operar con \(\left( {3,5} \right)\) porque la matriz asociada opera con coordenadas. Debemos buscar las coordenadas de \(\left( {3,5} \right)\) en la base \(B\). \[\left( {3,5} \right) = \alpha \left( {0,1} \right) + \beta \left( {1,1} \right) \Rightarrow \beta = 3{\rm{\;}},{\rm{\;}}\alpha = 2\] Multiplicamos la matriz por las coordenadas que obtuvimos,
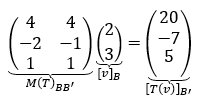
El vector obtenido no es el transformado del vector (3,5) sino que son sus coordenadas en la base \(B’\).
Para hallar \(T\left( {3,5} \right)\) debemos multiplicar las coordenadas obtenidas por los vectores de la base B’:
\[T\left( {\left( {3,5} \right)} \right) = 20\left( {1,0,0} \right) – 7\left( {1,1,0} \right) + 5\left( {0,1,1} \right)\] \[T\left( {\left( {3,5} \right)} \right) = \left( {13, – 2,{\rm{\;}}5} \right)\]
Ahora en lugar de tomar estas bases, tomemos las bases canónicas de \({\mathbb{R}^2}\) y de \({\mathbb{R}^3}\).
Busquemos \(M{\left( T \right)_{{E_2}{E_3}}}\) dónde:
\[{E_2} = \left\{ {\left( {1,0} \right),\left( {0,1} \right)} \right\}{\rm{\;}}\] \[{E_3} = \left\{ {\left( {1,0,0} \right),\left( {0,1,0} \right),\left( {0,0,1} \right)} \right\}{\rm{\;}}\]
El procedimiento es el mismo pero las cuentas son más fáciles
\[T\left( {\left( {1,0} \right)} \right) = \left( {1,1,0} \right) = \alpha \left( {1,0,0} \right) + \beta .\left( {0,1,0} \right) + \gamma .\left( {0,0,1} \right) \Rightarrow {\rm{\;}}\left( {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}1\\1\end{array}}\\0\end{array}} \right){\rm{\;}}1^\circ {\rm{\;}}columna\] \[T\left( {\left( {0,1} \right)} \right) = \left( {2, – 1,1} \right) = \alpha .\left( {1,0,0} \right) + \beta .\left( {0,1,0} \right) + \gamma .\left( {0,0,1} \right) \Rightarrow {\rm{\;}}\left( {\begin{array}{*{20}{c}}2\\{\begin{array}{*{20}{c}}{ – 1}\\1\end{array}}\end{array}} \right){\rm{\;\;}}2^\circ {\rm{\;}}columna\]
Estos vectores hay que expresarlos en coordenadas respecto de la base canónica de R3, pero justamente por tratarse de la base canónica, el vector y sus coordenadas son iguales. Entonces resulta:
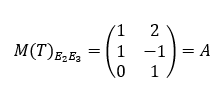
¡Qué es la matriz estándar de la TL! Es decir que la matriz estándar es la que trabaja con las bases canónicas.
Ejemplo 4
Consideremos la siguiente transformación lineal: \[F:{\mathbb{R}^2} \to {P_1}{\rm{\;\;}}|{\rm{\;\;}}M{\left( F \right)_{BB’}} = \left( {\begin{array}{*{20}{c}}1&2\\1&2\end{array}} \right)\] \[B = \left\{ {\left( {1,0} \right),\left( {1,1} \right)} \right\}\] \[B’ = \left\{ {\color{blue}{1},{\rm{\;}}\color{blue}{1 – x}} \right\}\]
a) Hallar \(F\left( {\left( {2,1} \right)} \right)\)
b) Hallar la fórmula de la transformación lineal
c) Hallar el núcleo de la transformación lineal
d) Hallar la imagen de la transformación lineal
e) Hallar la imagen de la transformación pero sin utilizar la fórmula de la transformación lineal
f) Hallar el núcleo de la transformación sin utilizar la fórmula
Resolución
Ítem a
No tenemos la fórmula. Tenemos que trabajar con la matriz asociada. ¿Qué propiedad tiene la matriz asociada? \[M{\left( F \right)_{BB{\rm{‘}}}}.{\left[ v \right]_B} = {\left[ {F\left( v \right)} \right]_{B{\rm{‘}}}}\]
Donde:
- \({\left[ v \right]_B}\): son las coordenadas del vector \(v\) en la base \(B\)
- \({\left[ {F\left( v \right)} \right]_{B’}}\): son las coordenadas del transformado del vector \(v\) en la base \(B’\)
- \(M{\left( F \right)_{BB’}}\): es la matriz asociada a la transformación lineal en bases \(B\) y \(B’\)
Las matrices asociadas no operan con los vectores, sino con las coordenadas de los vectores en alguna base. Entonces no podemos multiplicar la matriz por el vector \(\left( {2,1} \right)\).
Para operar, tenemos que encontrar las coordenadas de \(\left( {2,1} \right)\) en la base \(B\):
\[\left( {2,1} \right) = \alpha \left( {1,0} \right) + \beta \left( {1,1} \right){\rm{\;\;\;\;\;\;}} \Rightarrow {\rm{\;\;\;\;\;\;\;\;}}\alpha = 1 \wedge \beta = 1{\rm{\;\;\;\;\;\;\;\;\;\;}} \Rightarrow {\rm{\;\;\;\;\;\;}}{\left[ {\left( {2,1} \right)} \right]_B} = \left( {\begin{array}{*{20}{c}}1\\1\end{array}} \right)\]
Ahora multiplicamos por la matriz y obtenemos las coordenadas en \(B’\) del transformado de \(\left( {2,1} \right)\):
\[{\left[ {F\left( {\left( {2,1} \right)} \right)} \right]_{B{\rm{‘}}}} = \left( {\begin{array}{*{20}{c}}1&2\\1&2\end{array}} \right)\left( {\begin{array}{*{20}{c}}1\\1\end{array}} \right) = \left( {\begin{array}{*{20}{c}}\color{#F05}{3}\\\color{#F05}{3}\end{array}} \right)\]
¿Qué objeto esperamos obtener como imagen de esta transformación?
¿Un vector de \({\mathbb{R}^2}\)? No, esperamos obtener un polinomio de grado menor o igual que uno.
Para obtener \(F\left( {\left( {2,1} \right)} \right)\) debemos multiplicar estas coordenadas por los vectores de la base \(B’\):
\[F\left( {\left( {2,1} \right)} \right) = \color{#F05}{3}.\color{blue}{1} + \color{#F05}{3}.\left( {\color{blue}{1-x}} \right) = 6 – 3x\]
Ítem b
En el ítem (a) buscamos la imagen del vector \(\left( {2,1} \right)\). Ahora nos proponemos obtener la fórmula de la transformación, esto significa encontrar la imagen de cualquier vector \(\left( {x,\;y} \right)\) de \({\mathbb{R}^2}\). Teniendo en cuenta que en el polinomio usamos la variable \(x\), llamaremos \(\left( {a,b} \right)\) a los vectores de R2.
Busquemos \(F\left( {\left( {a,b} \right)} \right)\) tal como buscamos \(F\;\left( {\left( {2,1} \right)} \right)\): \[\left( {a,b} \right) = \alpha \left( {1,0} \right) + \beta \left( {1,1} \right) \Rightarrow {\rm{\;}}\left\{ {\begin{array}{*{20}{c}}{a = \alpha + \beta }\\{b = \beta }\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{\alpha = a – b}\\{\beta = b}\end{array}} \right.\] \[{\left[ {\left( {a,b} \right)} \right]_B} = \left( {\begin{array}{*{20}{c}}{a – b}\\b\end{array}} \right)\]
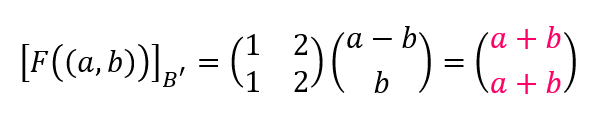
Éstas son las coordenadas del vector que estamos buscando. Falta multiplicar por los vectores de la base B’:
\[F\left( {\left( {a,b} \right)} \right) = \left( {\color{#F05}{a + b}} \right).\color{blue}{1} + \left( {\color{#F05}{a + b}} \right)\left( {\color{blue}{1-x}} \right) = 2a + 2b – \left( {a + b} \right).x\]
Ésta es la fórmula de la transformación lineal.
Ahora podemos hallar base y dimensión de núcleo e imagen.
Ítem c
La definición de núcleo dice que son los vectores del dominio que se transforman en el vector nulo del codominio.
\[ – \left( {a + b} \right)x + 2\left( {a + b} \right) = {0_{{P_1}}} = 0x + 0\] \[ \Rightarrow {\rm{\;}}\left\{ {\begin{array}{*{20}{c}}{a + b = 0}\\{a + b = 0}\end{array} \Rightarrow a = – b} \right.\] \[ \Rightarrow Nu\left( F \right) = \left\{ {\left( {a, – a} \right) \in {\mathbb{R}^2}} \right\} \Rightarrow {B_{Nu}} = \left\{ {\left( {\begin{array}{*{20}{c}}{ – 1}\\1\end{array}} \right)} \right\}{\rm{\;\;}} \Rightarrow {\rm{\;\;}}\dim \left( {Nu\left( F \right)} \right) = 1\]
Ítem d
Por el teorema de las dimensiones:
\[\dim \left( {Im\left( F \right)} \right) = \dim \left( {{\mathbb{R}^2}} \right) – \dim \left( {Nu\left( F \right)} \right) = 1\]
Queremos una base de la imagen. ¿En qué espacio vectorial está la imagen? En \({P_1}\).
Recordemos que los transformados de una base (cualquiera) del dominio, generan la imagen de la transformación lineal: \[F\left( {\left( {1,0} \right)} \right) = 2 – x\] \[F\left( {\left( {0,1} \right)} \right) = 2 – x\]
Entonces ¿Cuál es una base de la imagen de la transformación lineal?
\[{B_{Im}} = \left\{ {2 – x} \right\}\]
Veamos que la imagen no depende de la base del dominio que elijamos. Por ejemplo tomemos la base \(B\):
\[F\left( {\left( {1,0} \right)} \right) = 2 – x\] \[F\left( {\left( {1,1} \right)} \right) = 4 – 2x\] \[\left\{ {{\rm{\;}}2 – x{\rm{\;}},{\rm{\;}}4{\rm{\;}}–{\rm{\;}}2x{\rm{\;}}} \right\}\] generan \[Im\left( F \right)\] \[{B_{Im}} = \left\{ {2 – x} \right\}\]
Ítem e
No es necesario buscar la fórmula para obtener la imagen. Las columnas en la matriz nos dan las coordenadas en la base \(B’\) de los transformados de una base del dominio:
\[M{\left( F \right)_{BB’}} = \left( {{{\left[ {F\left( {{v_1}} \right)} \right]}_{B’}}{\rm{\;\;\;\;}}{{\left[ {F\left( {{v_2}} \right)} \right]}_{B’}}{\rm{\;}}} \right) = \left( {\begin{array}{*{20}{c}}1&2\\1&2\end{array}} \right)\]
Entonces:
\[F\left( {\left( {1,0} \right)} \right) = 1.1 + 1.\left( {1 – x} \right) = 2 – x\] \[F\left( {1,1} \right) = 2.1 + 2\left( {1 – x} \right) = 4 – 2x\]
Luego:
\[Im\left( F \right) = gen\left\{ {2 – x{\rm{\;}},{\rm{\;}}4 – 2x} \right\}\]
Cómo \(4 – 2x\) es combinación lineal de \(2 – x\) podemos quedarnos con la siguiente base: \[{B_{Im\left( F \right)}} = \left\{ {2 – x} \right\}\]
Ítem f
¿Y para el núcleo sin la fórmula? Queremos hallar los \(v \in {\mathbb{R}^2}\) tales que al aplicarles la transformación den por resultado el polinomio nulo:
\[F\left( v \right) = {0_{{P_1}}}\]
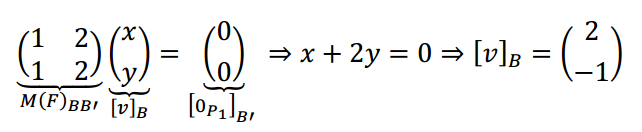
Éstas son las coordenadas en la base \(B\) de una base del núcleo:
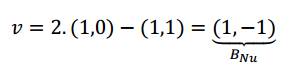
Ejemplo 5
Vamos a retomar el ejercicio 8, ítem a, de página 40 que decía:
Halle la expresión analítica de la siguiente transformación: Simetría respecto de la recta \(y = 3x,\;\;\;\;\;{\mathbb{R}^2} \to {\mathbb{R}^2}\)
En un ejemplo anterior habíamos obtenido la fórmula de la transformación lineal:
\[T\left( {\left( {x,y} \right)} \right) = \left( { – \frac{4}{5}x + \frac{3}{5}y{\rm{\;}};\frac{3}{5}x + \frac{4}{5}y} \right)\]
La matriz estándar (referida a la base canónica de\({\mathbb{R}^2}\)), \(M{\left( T \right)_{EE}}\) es la siguiente: \[M\left( T \right) = \left( {\begin{array}{*{20}{c}}{ – \frac{4}{5}}&{\frac{3}{5}}\\{\frac{3}{5}}&{\frac{4}{5}}\end{array}} \right)\]
Observación: cuando se trata de las bases canónicas para simplificar la notación se escribe \(M\left( T \right)\) en lugar de \(M{\left( T \right)_{EE}}\).
Veamos si podemos hallar una representación matricial más sencilla para esta simetría.
¿Qué significa una simetría respecto de la recta \(y = 3x\)? Recordemos que el transformado de un vector que esté sobre la recta es el mismo vector, y el transformado de un vector perpendicular a la recta es su opuesto.
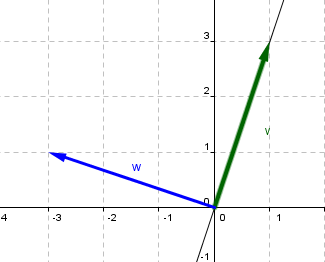
Armemos una base de \({\mathbb{R}^2}\) formada por un vector v sobre la recta ( \(y\; = \;3x\) ) y un vector w perpendicular a dicha recta. Por ejemplo:
\[B = \left\{ {\left( {1,3} \right),\left( { – 3,1} \right)} \right\}\] \[T\left( {\left( {1,3} \right)} \right) = \left( {1,3} \right) = 1.\left( {1,3} \right) + 0\left( { – 3,1} \right){\rm{\;}} \Rightarrow {\rm{\;\;}}{\left[ {\left( {1,3} \right)} \right]_B} = \left( {\begin{array}{*{20}{c}}1\\0\end{array}} \right)\] \[T\left( {\left( { – 3,1} \right)} \right) = \left( {3, – 1} \right) = 0.\left( {1,3} \right) + \left( { – 1} \right).\left( { – 3,1} \right){\rm{\;}} \Rightarrow {\left[ {\left( { – 3,1} \right)} \right]_{B’}} = \left( {\begin{array}{*{20}{c}}0\\{ – 1}\end{array}} \right)\]
¿Cuál es la matriz asociada a la transformación lineal en esta nueva base?
\[M{\left( T \right)_{BB}} = \left( {\begin{array}{*{20}{c}}1&0\\0&{ – 1}\end{array}} \right)\]
Eligiendo una base conveniente, pudimos caracterizar la simetría mediante una matriz diagonal. Continuaremos desarrollando este tema en la próxima unidad (autovalores y autovectores).
Ejercicio para el lector 3
Dada la transformación lineal \(F\) de \({\mathbb{R}^3}\) a \({P_1}\) cuya matriz asociada es:
\[M{\left( F \right)_{BE}} = \left( {\begin{array}{*{20}{c}}1&0&1\\{ – 1}&0&0\end{array}} \right)\]
siendo \(B = \left\{ {\left( {1,0,0} \right)\;,\;\left( {1,1,0} \right)\;,\;\left( {1,0,1} \right)} \right\}\) y \(E\; = \;\left\{ {\;1\;,\;t\;} \right\}\) bases de \({\mathbb{R}^3}\) y \({P_1}\) respectivamente.
a) Hallar una base del núcleo de \(F\). A partir de la base obtenida, ¿es posible afirmar que \(F\) es sobreyectiva? ¿Por qué?
b) Hallar todos los \(v \in {\mathbb{R}^3}\) tales que \(F\left( v \right) = – 1 + t\).
El rango es igual a la dimensión de la imagen
Recordemos que:
- \(M{\left( T \right)_{BB{\rm{‘}}}} = \left( {{{\left[ {T\left( {{v_1}} \right)} \right]}_{B{\rm{‘}}}}{\rm{\;\;}},{\rm{\;}} \ldots ,{{\left[ {T\left( {{v_n}} \right)} \right]}_{B{\rm{‘}}}}} \right)\)
- \(\left\{ {T\left( {{v_1}} \right), \ldots ,T\left( {{v_n}} \right)} \right\}\) generan \(Im\left( T \right)\)
Para obtener una base de \(Im\left( T \right)\) tenemos que determinar cuántos son LI. Se puede demostrar que en \(\left\{ {T\left( {{v_1}} \right), \ldots ,T\left( {{v_n}} \right)} \right\}\) habrá tantos vectores LI como columnas LI en la matriz. Dado que el rango de una matriz es el número de columnas LI, entonces el rango de la matriz asociada a la transformación lineal respecto de las bases \(B\) y es igual a la dimensión de la imagen de la trasformación lineal.
Observación: La dimensión de la imagen no depende de las bases elegidas, por esto el rango tampoco depende de ellas.
Ejercicio para el lector 4
Sea \(T:{\mathbb{R}^2} \to {\mathbb{R}^3}\) una transformación lineal tal que su matriz estándar es: \(M\left( T \right) = \left( {\begin{array}{*{20}{c}}1&2\\1&a\\0&{ – 1}\end{array}} \right) \in {\mathbb{R}^{3 \times 2}}\)
- Probar que \(T\) es inyectiva (monomorfismo) para todo \(a\) perteneciente a los reales.
- Hallar el valor de \(a\) tal que \(\left( { – 1, – 1,\;\;4} \right)\) pertenezca a la imagen de la transformación.
Videos relacionados

