Queremos construir una matriz que nos permita cambiar las coordenadas de un vector en una base por las coordenadas del mismo vector en otra base. Consideremos en un espacio vectorial \(V\) la función identidad, que transforma cada vector en sí mismo. Dejamos a cargo del lector demostrar que es una T.L. \[Id:V \to V{\rm{\;}}|{\rm{\;}}Id\left( v …
Archivos para noviembre 2016
Composición e inversa de transformaciones lineales
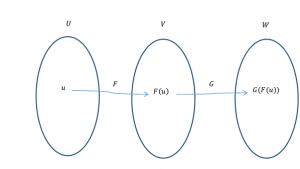
Composición de transformaciones lineales Sean \(F\) y \(G\) dos transformaciones lineales tales que: \[F:U \to V{\rm{\;\;\;}};{\rm{\;\;\;\;\;}}G:V \to W\] \[\exists GoF:U \to W{\rm{\;}}|{\rm{\;}}GoF\left( u \right) = G\left( {F\left( u \right)} \right){\rm{\;\;}}\forall u \in U\] Propiedad: la composición de transformaciones lineales, es …
[Leer más...] acerca deComposición e inversa de transformaciones lineales
Matriz asociada a una transformación lineal
Ejemplos introductorios Ejemplo 1 Sea \(T\) la siguiente transformación lineal: \[T:{\mathbb{R}^2} \to {\mathbb{R}^3}{\rm{\;}}|{\rm{\;\;}}T\left( {\left( {x,y} \right)} \right) = \left( {x + 2y,x - y,y} \right)\] ¿Existirá una matriz \(A\) que multiplicada por \(\left( {x,y} \right)\) dé por resultado \(\left( {x + 2y,x - y,y} \right)\)? Para esto …
[Leer más...] acerca deMatriz asociada a una transformación lineal