Hemos visto que:
\(\lambda \) es autovalor de \(A\) \( \Leftrightarrow \) \(\det \left( {A – \lambda I} \right) = 0\)
Es decir que los autovalores son las raíces del polinomio característico. La multiplicidad algebraica de un autovalor \(\lambda \) es su multiplicidad como raíz del polinomio característico \(p\left( \lambda \right)\). Denotaremos \({m_\lambda }\) a la multiplicidad algebraica del autovalor \(\lambda \).
Ejemplo
Supongamos \(A \in {\mathbb{R}^{5 \times 5}}\). \(p\left( \lambda \right) = – \;\lambda .\left( {\lambda – 1} \right).{\left( {\lambda – 2} \right)^3}\). Tiene grado 5. En la siguiente tabla resumimos los autovalores de \(A\) y sus multiplicidades algebraicas.
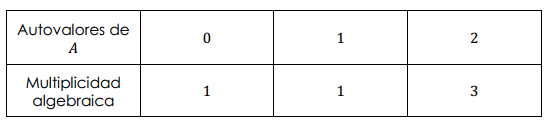
La multiplicidad geométrica de un autovalor \(\lambda \) es la dimensión del autoespacio asociado.
Ejemplo
Consideremos la siguiente matriz: \[B = \left( {\begin{array}{*{20}{c}}3&2&{ – 1}\\2&3&1\\0&0&5\end{array}} \right)\] Hemos visto que su polinomio característico es: \[{p_B}\left( \lambda \right) = – {\left( {\lambda – 5} \right)^2}\left( {\lambda – 1} \right)\] Observación. El coeficiente principal de los polinomios característicos asociados a las matrices \(n \times n\) es \({\left( { – 1} \right)^n}\). Así que si la matriz es de \(3 \times 3\) el coeficiente principal es \({\left( { – 1} \right)^3} = – 1\). Si la matriz es de \(2 \times 2\) el coeficiente principal será \({\left( { – 1} \right)^2} = 1\). Consideremos sus autovalores, la multiplicidad algebraica, y la multiplicidad geométrica:

Coinciden \({m_\lambda }\) con \(\dim \left( {{S_\lambda }} \right)\). Uno podría llegar a pensar que esto pasa siempre. Pero… Veamos que no es así. Tomemos la siguiente matriz:
\[M = \left( {\begin{array}{*{20}{c}}3&2&1\\2&3&1\\0&0&5\end{array}} \right)\]
Pueden verificar que el polinomio característico de M coincide con el de B: \[{p_M}\left( \lambda \right) = – {\left( {\lambda – 5} \right)^2}\left( {\lambda – 1} \right)\] Calculemos el autoespacio asociado al autovalor \(\lambda = 5\) \[\left( {\begin{array}{*{20}{c}}{ – 2}&2&1\\2&{ – 2}&1\\0&0&0\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\{\begin{array}{*{20}{c}}y\\z\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}0\\0\end{array}}\end{array}} \right)\;\] Esta matriz es de rango 2. Entonces ahora da como autoespacio una recta, no un plano. La dimensión del autoespacio será 1. \[\left\{ {\begin{array}{*{20}{c}}{ – 2x + 2y + z = 0}\\{2x – 2y + z = 0}\end{array} \Rightarrow z = 0\; \wedge x = y} \right.\] Entonces \[{S_5} = gen\left\{ {\left( {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}1\\1\end{array}}\\0\end{array}} \right)} \right\}\] Ahora el autoespacio asociado a \(\lambda = 1\) \[\left( {\begin{array}{*{20}{c}}2&2&1\\2&2&1\\0&0&4\end{array}} \right).\left( {\begin{array}{*{20}{c}}x\\{\begin{array}{*{20}{c}}y\\z\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}0\\0\end{array}}\end{array}} \right) \Rightarrow z = 0 \wedge x = – y\] \[{S_1} = gen\left\{ {\left( {\begin{array}{*{20}{c}}1\\{\begin{array}{*{20}{c}}{ – 1}\\0\end{array}}\end{array}} \right)} \right\}\] Entonces si hacemos el cuadro para la matriz \(M\), resulta:

Esto marca la diferencia entre matrices diagonalizables y no diagonalizables.
Nosotros estamos apuntando a diagonalizar una matriz, por lo cual esta diferencia que encontramos entre B y M será crucial.
Propiedad sobre multiplicidad algebraica y geométrica
Para cada autovalor \(\lambda \) de una matriz A, se verifica que: \[\dim \left( {{{\bf{S}}_{\bf{\lambda }}}} \right) \le {{\bf{m}}_{\bf{\lambda }}}\] ¿Puede ser cero la dimensión del autoespacio? ¿Qué querría decir que sea 0? Si la dimensión de un autoespacio fuera cero, significaría que contiene sólo al vector nulo, pero sabemos que el vector nulo no es un autovector. Entonces: \[{S_\lambda } \ne \left\{ {{0_V}} \right\} \Rightarrow \dim \left( {{S_\lambda }} \right) \ge 1\]
Por lo tanto, resulta:
Consecuencia: si \(\lambda \) es un autovalor simple (\({m_\lambda } = 1\)) entonces \(\dim \left( {{S_\lambda }} \right) = 1\).
Ejemplo 1
a) Dada la matriz \(A = \left( {\begin{array}{*{20}{c}}1&1&2\\2&2&4\\0&0&c\end{array}} \right)\) , hallar todos los valores de \(c\) para los cuales \(A\) es diagonalizable. b) Para \(c\; = \;0\) , hallar si es posible \(P\) inversible y \(D\) diagonal tales que:\({P^{ – 1}}AP = D\) .
Resolución
Vimos que:
\(A\;\;\)es diagonalizable si existe \(\;P\;\)inversible tal que \({P^{ – 1}}AP = D\;\;\;\)(diagonal)
Para armar \(P\) inversible, necesitamos tres autovectores LI (que serán las columnas de P).
Teniendo en cuenta que los autovectores asociados a autovalores distintos son L.I., podemos afirmar lo siguiente:
Si todos los autovalores son distintos, la matriz es diagonalizable porque podemos hallar tres autovectores LI.
Ahora bien: ¿qué ocurre si hay autovalores repetidos? En ese caso no podemos anticipar nada, tenemos que analizar cada caso por separado para comparar la multiplicidad algebraica del autovalor con la dimensión del autoespacio correspondiente.
Hallemos los autovalores de A, que son las raíces del polinomio característico: \[{\rm{p}}\left( {\rm{\lambda }} \right) = \det \left( {\begin{array}{*{20}{c}}{1 – \lambda }&1&2\\2&{2 – \lambda }&4\\0&0&{c – \lambda }\end{array}} \right) = \left( {c – \lambda } \right)\left[ {\left( {1 – \lambda } \right)\left( {2 – \lambda } \right) – 2} \right]\] \[ = \left( {c – \lambda } \right)\left[ { – 3\lambda + {\lambda ^2}} \right] = \left( {c – \lambda } \right)\lambda \left( { – 3 + \lambda } \right)\] Entonces los autovalores son: \[\lambda = c\;\;\; \vee \;\;\;\lambda = 0\;\;\;\; \vee \;\;\;\lambda = 3\] Veamos cómo separar los distintos casos para realizar un análisis completo:
Caso 1: \(c \ne 0\;\;\;y\;\;\;c \ne 3\) En este caso los tres autovalores son distintos, y por lo tanto \(A\) es diagonalizable.
Caso 2: \(c = 3\;\) En este caso los autovalores son: \(\lambda = 3\;\left( {doble} \right)\;y\;\;\lambda = 0\) Nos tenemos que centrar en el autovalor doble: ¿qué dimensión tiene el autoespacio? \[\left( {\begin{array}{*{20}{c}}{1 – 3}&1&2\\2&{2 – 3}&4\\0&0&{3 – 3}\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\{\begin{array}{*{20}{c}}y\\z\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}0\\0\end{array}}\end{array}} \right)\;\; \Rightarrow \;\;\left\{ {\begin{array}{*{20}{c}}{ – 2x + y + 2z = 0}\\{2x – y + 4z = 0}\end{array}} \right.\; \Rightarrow \;\left\{ {\begin{array}{*{20}{c}}{y = 2x}\\{z = 0}\end{array}} \right.\] Obtenemos entonces \({S_3} = gen\left\{ {\;\left( {\begin{array}{*{20}{c}}1\\2\\0\end{array}} \right)\;} \right\}\) Como el autovalor es doble y el autoespacio tiene dimensión 1, A no es diagonalizable. ¿Por qué? Porque con un autovector de \({S_3}\) y un autovector de \({S_0}\) no podemos completar los 3 autovectores L.I. que necesitamos para armar P. ¿Es necesario hallar \({S_0}\)? No, porque sabemos que tiene dimensión 1.
Caso 3: \(c = 0\) En este caso los autovalores son: \(\lambda = 0\;\left( {doble} \right)\) y \(\lambda = 3\left( {simple} \right)\). Autoespacio asociado a \(\lambda = 0\): \[\left( {\begin{array}{*{20}{c}}1&1&2\\2&2&4\\0&0&0\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\{\begin{array}{*{20}{c}}y\\z\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}0\\0\end{array}}\end{array}} \right)\;\; \Rightarrow \;\left\{ {\begin{array}{*{20}{c}}{x + y + 2z = 0}\\{2x + 2y + 4z = 0}\end{array}} \right. \Rightarrow \;\;x + y + 2z = 0\; \Rightarrow \left( { – y – 2z,y,z} \right)\] \[{S_0} = gen\left\{ {\;\left( {\begin{array}{*{20}{c}}{ – 1}\\1\\0\end{array}} \right)\;,\;\left( {\begin{array}{*{20}{c}}{ – 2}\\0\\1\end{array}} \right)\;} \right\}\] Como la dimensión del autoespacio coincide con la multiplicidad algebraica del autovalor, A es diagonalizable. Si tomamos dos autovectores L.I. de \({S_0}\) y un tercer autovector de \({S_3}\) , tendremos los tres autovectores LI necesarios para armar una P inversible tal que: \({P^{ – 1}}A\;P = D\) , como se pide en el ítem (b). En conclusión \(A\) es diagonalizable \(\forall c \in \mathbb{R} – \left\{ 3 \right\}\).
Ítem b
Nos falta hallar el autoespacio asociado a \(\lambda = 3\) \[\left( {\begin{array}{*{20}{c}}{ – 2}&1&2\\2&{ – 1}&4\\0&0&{ – 3}\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\{\begin{array}{*{20}{c}}y\\z\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}0\\0\end{array}}\end{array}} \right)\;\;\; \Rightarrow \;\;\left\{ {\begin{array}{*{20}{c}}{ – 2x + y + 2z = 0}\\{2x – y + 4z = 0}\\{ – 3z = 0}\end{array}} \right.\;\; \Rightarrow \;\;\left\{ {\begin{array}{*{20}{c}}{y = 2x}\\{z = 0}\end{array}} \right.\;\;\; \Rightarrow \;\left( {x,2x,0} \right)\]
\[{S_{\lambda = 3}} = \;gen\left\{ {\;\left( {\begin{array}{*{20}{c}}1\\2\\0\end{array}} \right)\;} \right\}\]
\[P = \left( {\begin{array}{*{20}{c}}{ – 1}&{ – 2}&1\\1&0&2\\0&1&0\end{array}} \right)\;\;\;,\;\;\;D = \left( {\begin{array}{*{20}{c}}0&0&0\\0&0&0\\0&0&3\end{array}} \right)\]
El lector puede verificar que: \({P^{ – 1}}AP = D\)
Videos relacionados con autovalores y autovectores

