Definición de matrices semejantes
Sean \(A,B \in {\mathbb{R}^{n \times n}}\) , decimos que: \(A\) y \(B\) son matrices semejantes \( \Leftrightarrow \) \(\exists P \in {\mathbb{R}^{n \times n}}\) inversible tal que \(B = {P^{ – 1}}.A.P\) .
Ejemplo
Consideremos las siguientes matrices: \[B = \left( {\begin{array}{*{20}{c}}2&1\\0&1\end{array}} \right)\;\;\;\;\;\;\;\;\;\;A = \left( {\begin{array}{*{20}{c}}1&3\\0&2\end{array}} \right)\;\;\;\;\;\;\;\;\;\;\;P = \left( {\begin{array}{*{20}{c}}3&0\\1&1\end{array}} \right)\;\;\;\;\;\;\;\;\;\;\;{P^{ – 1}} = \left( {\begin{array}{*{20}{c}}{\frac{1}{3}}&0\\{ – \frac{1}{3}}&1\end{array}} \right)\] Podemos afirmar que \(B\) es semejante a \(A\) pues: \[B = {P^{ – 1}}.A.P\] \[B = \left( {\begin{array}{*{20}{c}}{\frac{1}{3}}&0\\{ – \frac{1}{3}}&1\end{array}} \right)\left( {\begin{array}{*{20}{c}}1&3\\0&2\end{array}} \right)\left( {\begin{array}{*{20}{c}}3&0\\1&1\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{\frac{1}{3}}&1\\{ – \frac{1}{3}}&1\end{array}} \right)\left( {\begin{array}{*{20}{c}}3&0\\1&1\end{array}} \right) = \left( {\begin{array}{*{20}{c}}2&1\\0&1\end{array}} \right)\]
Propiedad de las matrices semejantes
Si \(A\) y \(B\) son semejantes, tienen el mismo polinomio característico y por lo tanto, los mismos autovalores.
\[A\;y\;B\;semejantes \Rightarrow {p_A}\left( \lambda \right) = {p_B}\left( \lambda \right) \Rightarrow Tienen\;los\;mismos\;autovalores\]
Demostración
\[{p_A}\left( \lambda \right) = \det \left( {A – \lambda I} \right)\] \[{p_B}\left( \lambda \right) = \det \left( {B – \lambda I} \right)\]
Además sabemos que: \[A = {P^{ – 1}}BP\]
Entonces:
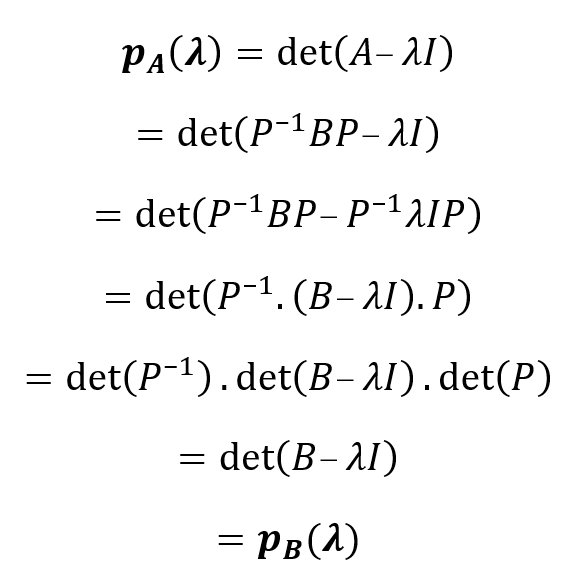
Donde hemos reemplazado \(\lambda I\) por \({P^{ – 1}}\lambda IP\) ya que: \[{P^{ – 1}}\lambda IP = \lambda .{P^{ – 1}}P = \lambda I\] Y hemos utilizado la propiedad distributiva del determinante respecto de la multiplicación de matrices.

