Definición de lugar geométrico
Dada una ecuación \(F\left( {x,y} \right) = 0\) se denomina lugar geométrico al conjunto de los puntos \(P\left( {x,y} \right)\) de \({\mathbb{R}^2}\) que verifican la ecuación.
Ejemplo 1
Consideremos que la ecuación \(F\left( {x,y} \right) = 0\) es:
\[{x^2} – 4xy = 0\]
¿Qué tipo de lugar geométrico representa? Dicho de otro modo, ¿qué curva determinan los puntos que verifican esta ecuación? Si sacamos factor común \(x\) queda:
\[x.\left( {x – 4y} \right) = 0\;\]
¿Cuándo un producto de dos factores es igual a cero? Cuando alguno de los dos es igual a cero:
\[x = 0 \vee x = 4y\]
¿Qué representa geométricamente cada una de estas ecuaciones?
- \(x = 0\) es la ecuación del el eje \(y\)
- \(x = 4y\) es una recta de pendiente \(\frac{1}{4}\).
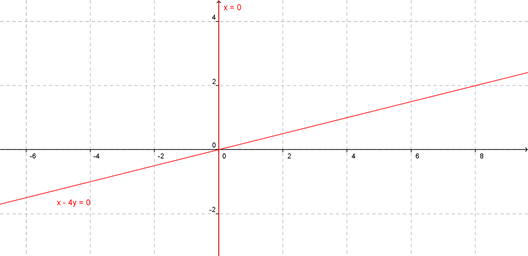
Es decir que el lugar geométrico es un par de rectas no paralelas.
Ejemplo 2
Veamos este otro ejemplo:
No existe lugar geométrico, porque no hay ningún punto que satisfaga la ecuación (es imposible que la suma de dos cuadrados dé por resultado un número negativo).
¿Qué son las cónicas?
Apolonio, contemporáneo de Arquímedes, en el siglo III antes de Cristo, estudió con mucha profundidad las curvas cónicas. El nombre de «cónicas» les viene de que son curvas que se obtienen de cortar un cono con diferentes planos, como muestra el siguiente esquema:
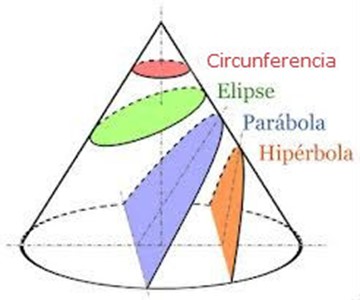
El cono en el que debemos pensar continúa más allá del vértice. Una imagen más adecuada para representar las cónicas es la siguiente:
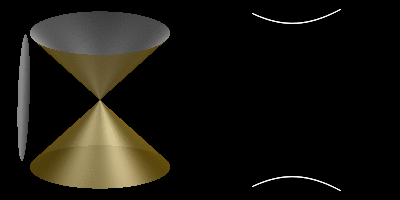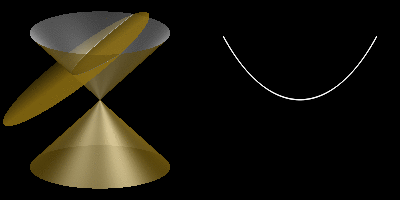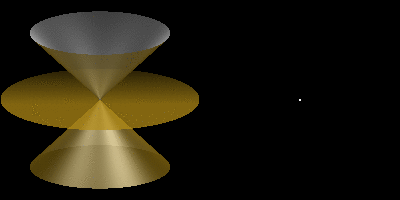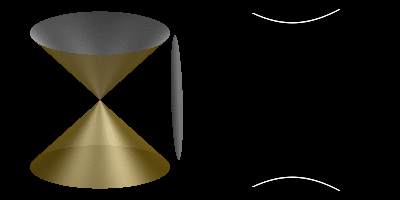
Las cónicas son curvas determinadas por la intersección de un cono circular recto con planos de distintas inclinaciones.
Videos relacionados con Cónicas

