Hipérbola

Introducción

Ustedes ya conocen a las hipérbolas como la representación gráfica de funciones homográficas. El ejemplo más sencillo es la gráfica de la función \(f\left( x \right) = \frac{1}{x}\):

A continuación estudiaremos las hipérbolas desde otra perspectiva.

Definición de hipérbola

\[\mathcal{H} = \left\{ {P\left( {x,y} \right)|\;\;\left| {d\left( {P;{F_1}} \right) – d\left( {P;{F_2}} \right)} \right| = 2a = cte} \right\}\]

Si la distancia entre los focos es \(d\left( {{F_1},{F_2}} \right) = 2c\) , la condición para que sea una hipérbola es:

\[c > a > 0\]
\[{c^2} > {a^2}\]
\[{c^2} – {a^2} = {b^2}\]
\[ \Rightarrow {c^2} = {a^2} + {b^2}\]

Ecuación canónica de la hipérbola

Con una deducción similar a la de la elipse, se obtiene:

Es la ecuación canónica de la hipérbola con centro en \(\left( {0,0} \right)\) y eje focal \(y = 0\) (eje \(x\))

Busquemos las intersecciones con los ejes:

\[y = 0\; \Rightarrow \;\left| x \right| = a \Rightarrow \;x = \pm a\; \Rightarrow {V_{1,2}} = \left( { \pm a,0} \right)\]

\[x = 0\;\; \Rightarrow {y^2} = – {b^2}\]

Entonces no corta al eje \(y\).

Los puntos \({V_{1,2}}\) se denominan vértices de la hipérbola.

Elementos de la hipérbola

\[\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\]

Focos: \({F_1}\left( {c,0} \right)\) y \({F_2}\left( { – c,0} \right)\)

Centro: \(C\;\left( {0,0} \right)\)

Vértices: \({V_1}\left( {a,0} \right)\) y \({V_2}\left( { – a,0} \right)\;\)

Eje focal: recta que contiene a los focos, en este caso es el eje \(x\)

a se denomina semieje real o transverso

b se denomina semieje imaginario

2c es la distancia entre los focos

Se cumple que \({c^2} = {a^2} + {b^2}\)

En la hipérbola aparece un elemento nuevo que no tiene ninguna de las otras cónicas: las asíntotas.

Ecuaciones de las asíntotas: \(y\; = \; \pm \frac{b}{a}\;\;x\)

Veamos la gráfica:

Ubiquemos los vértices sobre el eje \(x\), simétricos respecto del \(\left( {0,0} \right)\), \({V_{1,2}}\left( { \pm a,0} \right)\) y los puntos de coordenadas \(\;\left( {0, \pm \;b} \right)\) que llamaremos «vértices imaginarios» (no son puntos de la hipérbola, habíamos visto que ésta no corta al eje y):

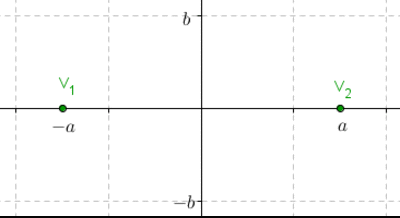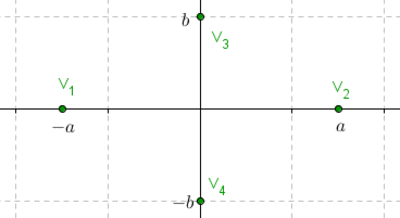
Para trazar las asíntotas armemos un rectángulo auxiliar que ayudará a graficar la hipérbola, y luego tracemos las rectas que contienen a sus diagonales (esas rectas serán las asíntotas). Una vez trazadas las asíntotas, es sencillo realizar un gráfico aproximado de la hipérbola:

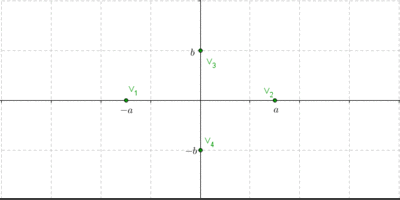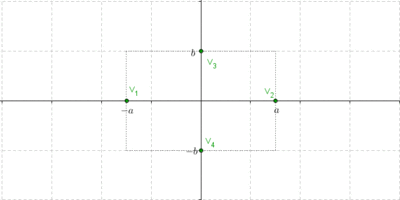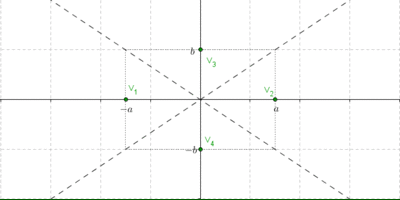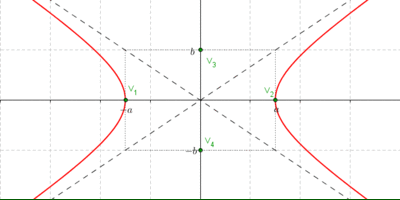
¿Cuáles son las pendientes de las diagonales?

Habíamos visto que las ecuaciones de las asíntotas son:

\(y\; = \; \pm \frac{b}{a}\;\;x\).

Esto justifica porqué las asíntotas son las rectas que contienen a las diagonales del rectángulo.

Los focos, como los vértices de la hipérbola, están sobre el eje x. Como \(c > a\), los focos están más alejados del origen que los vértices (\({c^2}\; = \;{a^2}\; + \;{b^2}\)).

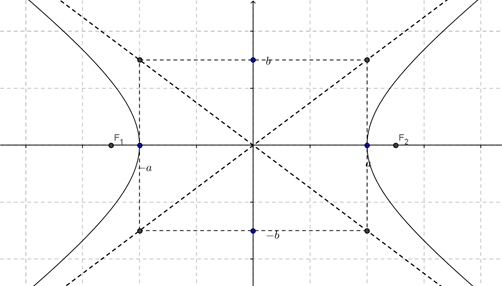
Si en la ecuación canónica anterior permutamos x por y queda:

Es la ecuación canónica de la hipérbola con centro en \(\left( {0,0} \right)\) y eje focal \(x = 0\) eje \(y\).

¿Cómo reconocer, dada la ecuación canónica de una hipérbola si el eje focal es vertical u horizontal?

• Si el coeficiente de \({x^2}\) es positivo, sabemos que el eje focal es el eje \(x\)
• Si el coeficiente de \({y^2}\) es positivo, sabemos que el eje focal es el eje \(y\)

Ejemplo 1

Hallar la gráfica de la curva definida por la ecuación:

\[{x^2}\; – \frac{{{y^2}}}{4}\; = \;1\]

Resolución

La ecuación responde a la forma canónica de una hipérbola con eje focal \(x\). Luego:

\[C\left( {0,0} \right)\]

\[Semieje\;real\;:\;a = 1\]

\[Semieje\;imaginario:\;b = 2\]

\[Semidistancia\;focal:c = \sqrt {{1^2} + {2^2}} = \sqrt 5 \]

Grafiquemos lo obtenido hasta el momento:

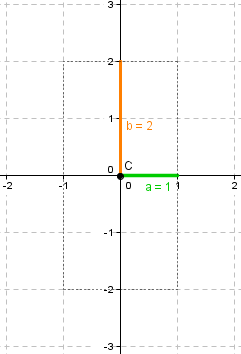
Luego podemos dar las coordenadas de los vértices, de los focos y de las asíntotas:

\[{V_1}\left( {1,0} \right)\]

\[{V_2}\left( { – 1,0} \right)\]

\[{F_1}\left( { – \sqrt 5 ,0} \right)\]

\[{F_2}\left( {\sqrt 5 ,0} \right)\]

\[Asíntotas:\;y = \pm 2x\]

La gráfica:

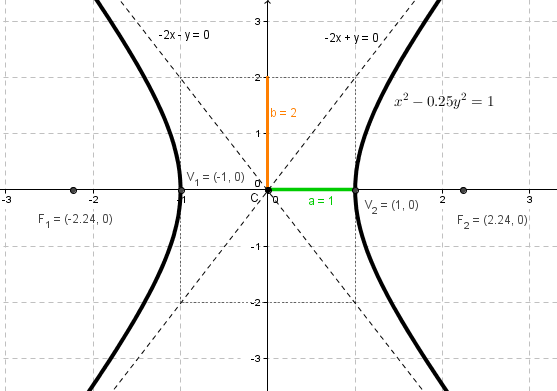
Ejemplo 2

Hallar la gráfica de la curva definida por la ecuación:

\[\frac{{{y^2}}}{4} – \frac{{{x^2}}}{6} = 1\]

Resolución

Como el coeficiente de \({y^2}\) es positivo, entonces el eje focal es el eje \(y\).

\({a^2} = 4 \to a = 2\;\) semieje real

\({b^2} = 6 \to \;\;b = \sqrt 6 \;\) semieje imaginario

Vértices \(\left( {0, \pm 2} \right)\)

¿Cómo se obtienen las coordenadas de los focos? Falta calcular el valor de \(c\) mediante la relación:

\({c^2} = {a^2} + {b^2}\; \Rightarrow \) \({c^2} = 10 \to c = \sqrt {10} \)

Focos \(\left( {0, \pm \sqrt {10} } \right)\)

Grafiquemos:

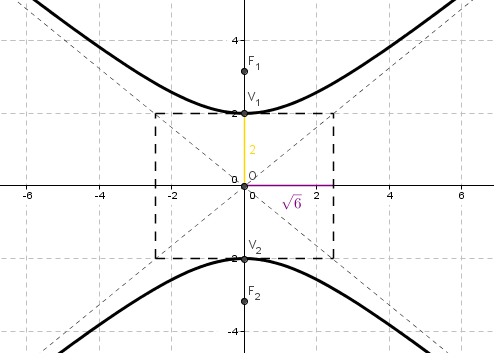
Como se puede deducir de la gráfica, las ecuaciones de las asíntotas son:

\[y = \frac{2}{{\sqrt 6 }}x\;\;\;\;\;,\;\;\;\;\;y = – \frac{2}{{\sqrt 6 }}x\]

Ejercicio para el lector 4

En el siguiente applet construido utilizando GeoGebra, se puede visualizar una familia de curvas que responden a la ecuación:

\[\frac{{{x^2}}}{4} – \frac{{{y^2}}}{{16}} = k\]

Moviendo con el cursor el deslizador se puede dar a \(k\) diferentes valores y observar cómo se modifica la curva:

Utilizando el applet les proponemos que respondan a las siguientes preguntas:

a) ¿Qué tipo de curvas se obtiene si \(k\) es distinto de \(0\)?

b) ¿Qué diferencia observan para valores de \(k > 0\) respecto de \(k < 0\)?

c) ¿Qué objeto geométrico se obtiene para \(k = 0\)?

De acuerdo con lo que pudimos observar en el applet podemos enunciar un método sencillo para buscar las ecuaciones de las asíntotas de una hipérbola.

Consideremos la siguiente ecuación:

\[\frac{{{x^2}}}{{{p^2}}} – \frac{{{y^2}}}{{{q^2}}} = k\;\;\;,\;\;\;\;k \ne 0\]

Según hemos visto al reemplazar \(k\) por \(0\) obtenemos las ecuaciones de las asíntotas:

\[\;\frac{{{x^2}}}{{{p^2}}} – \frac{{{y^2}}}{{{q^2}}} = 0\]

\[ \Rightarrow \;\;y = \pm \frac{q}{p}x\]

Ecuación ordinaria de una hipérbola

La ecuación ordinaria de una hipérbola con eje focal horizontal y centro en \(C\left( {\alpha ,\beta } \right)\) es:

La ecuación ordinaria de una hipérbola con eje focal vertical y centro en \(C\left( {\alpha ,\beta } \right)\)
es:

Observemos que la diferencia esencial reside en que el signo negativo está en el término con la variable \(x\) o en el término con la variable \(y\). El motivo por el cual utilizamos \({a^2}\) en el denominador del término con coeficiente positivo es para poder denominar siempre al semieje real como «\(a\)».

Casos particulares de hipérbolas

Hipérbola equilátera

Una hipérbola equilátera es aquella en la cual el semieje real es de igual longitud que el semieje imaginario. Es decir que su ecuación puede ser de la forma:

\[\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{a^2}}} = 1\;\;\;\;\;\;\;\;{\rm{\;o\;bien\;\;\;\;\;}}\;\; – \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{a^2}}} = 1\;\]

Hipérbolas conjugadas

Dos hipérbolas son conjugadas una de la otra si el eje real de cada una de ellas es igual al eje imaginario de la otra.

En términos analíticos se las reconoce porque los signos están cambiados, y los coeficientes de \(x\) y de \(y\) siguen siendo los mismos en términos absolutos. Las siguientes hipérbolas son conjugadas:

\[{\mathcal{H}_1}\;:\;\;\frac{{{x^2}}}{{{p^2}}} – \frac{{{y^2}}}{{{q^2}}} = 1\;\;\;\;\;\;\;\;\;\;\;{\mathcal{H}_2}\;\; – \frac{{{x^2}}}{{{p^2}}} + \frac{{{y^2}}}{{{q^2}}} = 1\;\]

Gráficamente:

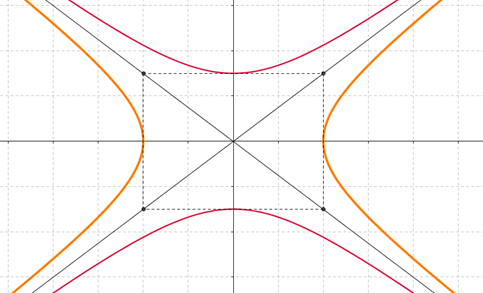
Cómo se aprecia en la gráfica las hipérbolas conjugadas tienen iguales asíntotas.

Ejemplo

Dada la ecuación en \({\mathbb{R}^2}\):

\[A{x^2} + {y^2} + By = 0\]

Hallar en cada caso, si es posible, los valores de \(A\) y \(B\) para que la ecuación dada represente:

a) Una elipse

b)Una circunferencia de radio 3

c) Una parábola

d) Un par de rectas paralelas

e) Una hipérbola equilátera con centro en \(C\left( {0,3} \right)\)

Resolución

Ítem a

Empecemos completando cuadrados para darle forma de ecuación ordinaria:

\[A{x^2} + {\left( {y + \frac{B}{2}} \right)^2} = {\left( {\frac{B}{2}} \right)^2}\;\; \Rightarrow \;\;\frac{{A{x^2}}}{{{{\left( {\frac{B}{2}} \right)}^2}}} + \frac{{{{\left( {y + \frac{B}{2}} \right)}^2}}}{{{{\left( {\frac{B}{2}} \right)}^2}}} = 1\;\;\left( {B \ne 0} \right)\;\;\]

Al estar igualada a 1, para que se trate de una elipse es necesario que el coeficiente de \({x^2}\) y el de \({y^2}\) sean ambos positivos. Una restricción para que la expresión tal como está escrita quede bien definida es que \(B \ne 0\). Como el coeficiente de \({y^2}\) será positivo siempre que \(B \ne 0\), entonces \(A\) deberá ser positivo también. Luego:

\[B \ne 0 \wedge A > 0\]

En particular si \(A = 1\) vemos que queda el mismo coeficiente para \({x^2}\) e \({y^2}\), y la curva es una circunferencia.

Ítem b

Ya establecimos que con \(A = 1\) será una circunferencia,

\[{x^2} + {\left( {y + \frac{B}{2}} \right)^2} = {\left( {\frac{B}{2}} \right)^2}\]

De radio

\[R = \sqrt {{{\left( {\frac{B}{2}} \right)}^2}} = \left| {\frac{B}{2}} \right|\]

Si queremos que el radio sea \(3\):

\[\left| {\frac{B}{2}} \right| = 3\; \Rightarrow \left| B \right| = 6\]

Luego la respuesta es:

\[A = 1 \wedge \left| B \right| = 6\]

Ítem c

Para que sea una parábola es necesario que una de las variables aparezca elevada al cuadrado y la otra no. Luego debe ser \(A = 0\). Pero queda:

\[{y^2} + By = 0\]

Que no responde a la ecuación de una parábola porque no ha quedado ningún termino lineal con \(x\). ¿Cuál es la curva con la que se corresponde esta ecuación entonces? Sacando factor común \(y\):

\[y.\left( {y + B} \right) = 0 \Rightarrow y = 0\; \vee y = – B\]

Es decir dos rectas horizontales y paralelas. En particular si \(B = 0\) queda una única recta.

Respuesta: no es posible.

Ítem d

Lo hemos respondido en el ítem anterior. Para que sean dos rectas paralelas:

\[A = 0 \wedge B \ne 0\]

Ítem e

Para analizar este caso utilicemos la expresión:

\[\;\;\frac{{A{x^2}}}{{{{\left( {\frac{B}{2}} \right)}^2}}} + \frac{{{{\left( {y + \frac{B}{2}} \right)}^2}}}{{{{\left( {\frac{B}{2}} \right)}^2}}} = 1\;\;\left( {B \ne 0} \right)\]

Si es una hipérbola los signos de los coeficientes de \({x^2}\) e \({y^2}\) deben ser distintos. Luego \(A\) debe ser negativo. Luego para que sea hipérbola debe ser:

\[A < 0 \wedge B \ne 0\]

Para ser equilátera tienen que ser iguales el eje real y el transverso, luego:

\[\frac{1}{{{A^2}}}.\frac{B}{2} = \frac{B}{2} \Rightarrow \left| A \right| = 1 \Rightarrow A = – 1\]

Luego para que sea hipérbola equilátera debe ser:

\[A = – 1 \wedge B \ne 0\]

Si queremos que el centro esté en \(\left( {0,3} \right)\) entonces:

\[\frac{B}{2} = – 3 \Rightarrow B = – 6\]

Respuesta:

\[A = – 1 \wedge B = – 6\]

En el siguiente archivo de GeoGebra podemos manipular los valores de los parámetros \(A\) y \(B\) para chequear si los resultados son correctos y explorar la forma que va tomando la curva para cada par de valores de los parámetros:

Cómo graficar hipérbolas en GeoGebra

En el siguiente video se puede ver cómo graficar hipérbolas usando GeoGebra.