Ecuaciones paramétricas de una recta en \({\mathbb{R}^2}\)
Nosotros ya vimos cómo parametrizar rectas en \({\mathbb{R}^2}\) y en \({\mathbb{R}^3}\):
Un ejemplo de parametrización de una recta sería:
\[\left\{ {\begin{array}{*{20}{c}}{x = 2t}\\{y = t – 1}\end{array}\;\;\forall t \in \mathbb{R}} \right.\]
\[t = \frac{x}{2}\]
\[y = \frac{x}{2} – 1\]
Esto es una recta con pendiente \(\frac{1}{2}\) y ordenada al origen igual a \( – 1\).
Veamos esta parametrización:
\[\left\{ {\begin{array}{*{20}{c}}{x = 2t}\\{y = t – 1}\end{array}\;\;\forall t \in \left[ {0,1} \right]} \right.\]
¿Es la parametrización de una recta? No estamos parametrizando toda la recta, sino un segmento de la recta. ¿Qué segmento estamos parametrizando? Para cada valor de \(t\), corresponde un punto \(\left( {x,y} \right)\) que pertenece a la recta, o en este cado al segmento de recta.
Veamos qué puntos corresponden para \(t = 0\) y para \(t = 1\):
\[t = 0 \Rightarrow \left( {0, – 1} \right)\]
\[t = 1 \Rightarrow \left( {2,0} \right)\]
Esto quiere decir que estamos parametrizando el segmento de recta que comprendido entre los puntos \(\left( {0, – 1} \right)\) y \(\left( {2,0} \right)\). ¿En qué sentido se recorre el segmento? ¿Desde \(\left( {0, – 1} \right)\) hacia \(\left( {2,0} \right)\) o en sentido contrario? El sentido viene dado por el valor inicial y final de t. En el siguiente archivo de GeoGebra se puede visualizar como para cada valor del parámetro se obtiene un punto distinto:
Ahora vamos a ver cómo parametrizar las cónicas.
Parametrización de la circunferencia
Queremos descomponer el movimiento circular en el eje \(x\) y en el eje \(y\).
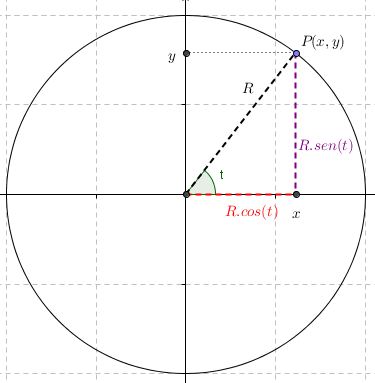
Con la ayuda de la trigonometría expresemos las coordenadas de un punto cualquiera en función de \(t\):
\[\left\{ {\begin{array}{*{20}{c}}{x = R.\cos \left( t \right)}\\{y = R.sen\left( t \right)}\end{array}} \right.\]
Si quiero dar toda la vuelta a la circunferencia \(t\) deberá estar en el intervalo
\[\left[ {0,2\pi } \right]\]
Obtuvimos así una parametrización de la circunferencia con \(C\left( {0,0} \right)\) y radio \(R\).
Si en esta parametrización se considera el intervalo \(\left[ {0,\frac{\pi }{2}} \right]\) ¿Qué arco de circunferencia queda descripto?
«Desparametrización» de la circunferencia
Para pasar desde las ecuaciones paramétricas a la cartesiana debemos eliminar el parámetro \(t\). Elevamos al cuadrado ambas igualdades:
\[{x^2} = {R^2}.{\cos ^2}\left( t \right)\]
\[{y^2} = {R^2}.se{n^2}\left( t \right)\]
Sumando las ecuaciones miembro a miembro:
\[{x^2} + {y^2} = {R^2}\]
Que es la ecuación canónica de la circunferencia.
Otra parametrización de la circunferencia
La ecuación canónica de una circunferencia con centro en \(\left( {0,0} \right)\) y de radio \(r\) es única:
\[{x^2} + {y^2} = {R^2}\]
Ahora consideremos:
\[{\rm{Parametrización\;}}2:\;\;\left\{ {\begin{array}{*{20}{c}}{x = R.sen\left( t \right)}\\{y = R.cos\left( t \right)}\end{array}\;\;\;\;\;\;\;\;\;\;\;t \in \left[ {0,2\pi } \right]} \right.\]
¿Qué curva representa esta parametrización? Es posible que no nos demos cuenta fácilmente. Intentemos obtener la ecuación cartesiana. Vamos a «desparametrizar» la curva. Podemos elevar al cuadrado ambos miembros:
\[\begin{array}{*{20}{c}}{{x^2} = {R^2}.se{n^2}\left( t \right)}\\{{y^2} = {R^2}.{{\cos }^2}\left( t \right)}\end{array}\]
\[{x^2} + {y^2} = {R^2}\]
Que es exactamente la misma curva que ya habíamos parametrizado. Entonces las ecuaciones paramétricas para una curva no son únicas. Representan la misma circunferencia con centro en \(\left( {0,0} \right)\) y radio \(R\). ¿Cuál es la diferencia entre ambas parametrizaciones?
Vamos a hacer una tabla para algunos valores para ver la diferencia entre las dos parametrizaciones.
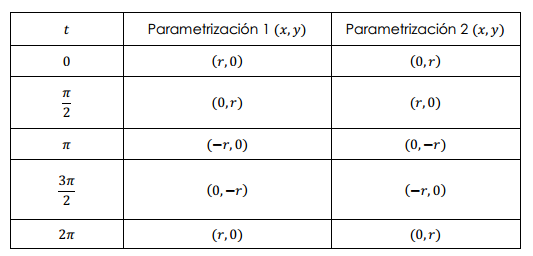
Es decir que la trayectoria es la misma pero el sentido en que se recorre la trayectoria cambia. En el primer caso es antihorario y en el otro, horario.
Ejercicio para el lector 5
Dada la parametrización:
\[\;\left\{ {\begin{array}{*{20}{c}}{x = 3.sen\left( {2t} \right)}\\{y = 3.cos\left( {2t} \right)}\end{array}\;\;\;\;\;\;\;\;\;\;\;t \in \left[ {0,2\pi } \right]} \right.\]
a) Eliminando el parámetro, identifiquen que curva representa.
b) Describan la diferencia entre esta parametrización y la parametrización:
\[\left\{ {\begin{array}{*{20}{c}}{x = 3.sen\left( t \right)}\\{y = 3.cos\left( t \right)}\end{array}\;\;\;\;\;\;\;\;\;\;\;t \in \left[ {0,2\pi } \right]} \right.\]
Ejemplo
Consideremos la siguiente parametrización:
\[\;\left\{ {\begin{array}{*{20}{c}}{x = 5.\cos \left( {2t} \right)}\\{y = 5.sen\left( {2t} \right)}\end{array}\;\;\;t \in \left[ {0,\frac{\pi }{2}} \right]} \right.\]
Si elevamos al cuadrado y sumamos, obtenemos:
\[{x^2} + {y^2} = 25\]
Construyamos la tabla de valores:
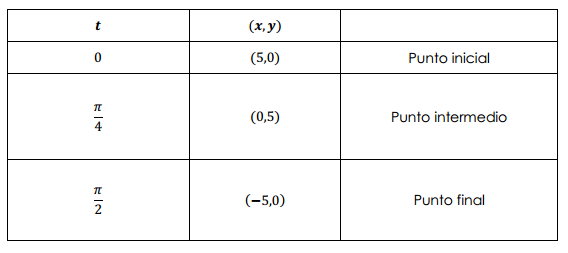
Es una semicircunferencia recorrida con sentido antihorario.
Ejemplo
Hallar una parametrización de la curva dada por:
\[{x^2} + {y^2} + x – 4y = 0\]
Indicar punto inicial \({P_0}\) y sentido de recorrido de la curva.
Resolución
Veamos cómo se podría resolver esto en forma general. Tratemos de llevar la ecuación a la forma ordinaria.
¿Qué curva podría representar esta ecuación?
Una circunferencia, porque los coeficientes de \({x^2}\) y de \({y^2}\) son iguales.
Consideremos la ecuación ordinaria:
\[{\left( {x – \alpha } \right)^2} + {\left( {y – \beta } \right)^2} = {r^2}\]
Dividamos ambos miembros por \({r^2}\) :
\[\frac{{{{\left( {x – \alpha } \right)}^2}}}{{{r^2}}} + \frac{{{{\left( {y – \beta } \right)}^2}}}{{{r^2}}} = 1\]
Lo expresemos como suma de cuadrados:
\[{\left( {\frac{{x – \alpha }}{r}} \right)^2} + {\left( {\frac{{y – \beta }}{r}} \right)^2} = 1\]
Aprovechemos la identidad trigonométrica, para realizar el siguiente cambio de variable:
\[cos\left( t \right) = \frac{{x – \alpha }}{r}\]
\[{\rm{sen}}\left( t \right) = \frac{{y – \beta }}{r}\]
Despejemos \(x\) e \(y\) para obtener una posible parametrización:
Estas son las ecuaciones paramétricas de la circunferencia con centro en el punto \(\left( {\alpha ,\beta } \right)\) y radio \(r\).
Retomemos el ejemplo:
\[{x^2} + {y^2} + x – 4y = 0\]
Completando cuadrados:
\[{\left( {x + \frac{1}{2}} \right)^2} – {\left( {\frac{1}{2}} \right)^2} + {\left( {y – 2} \right)^2} – {2^2} = 0\]
\[{\left( {x + \frac{1}{2}} \right)^2} + {\left( {y – 2} \right)^2} = \frac{1}{4} + 4\]
\[{\left( {x + \frac{1}{2}} \right)^2} + {\left( {y – 2} \right)^2} = \frac{{17}}{4}\]
Las coordenadas del centro y el valor del radio son:
\[\alpha = – \frac{1}{2}\]
\[\beta = 2\]
\[r = \frac{{\sqrt {17} }}{2}\]
Una posible parametrización es:
\[\left\{ {\begin{array}{*{20}{c}}{x = – \frac{1}{2} + \frac{{\sqrt {17} }}{2}\cos \left( t \right)}\\{y = 2 + \frac{{\sqrt {17} }}{2}.sen\left( t \right)}\end{array}\;\;\;t \in \left[ {0,2\pi } \right]} \right.\]
Parametrización de la elipse
Hallar una parametrización de la siguiente curva:
\[{x^2} + 4{y^2} – 2x + 4y + 1 = 0\]
Si los coeficientes de \({x^2}\) e \({y^2}\) no son iguales, no puede tratarse de una circunferencia. Tampoco puede ser una parábola. Entonces o es una elipse o es una hipérbola. Si fuera una hipérbola los signos de los coeficientes de los términos con \({x^2}\) e \({y^2}\) deberían ser distintos. Luego pensamos inicialmente que es una elipse.
Deberíamos llegar a una ecuación como ésta:
\[\frac{{{{\left( {x – \alpha } \right)}^2}}}{{{a^2}}} + \frac{{{{\left( {y – \beta } \right)}^2}}}{{{b^2}}} = 1\]
Una vez que lo escribimos así, es fácil parametrizar porque podemos expresar esto como la suma de dos cuadrados:
\[{\left( {\frac{{x – \alpha }}{a}} \right)^2} + {\left( {\frac{{y – \beta }}{b}} \right)^2} = 1\]
Y por la identidad pitagórica podemos hacer:
\[\cos \left( t \right) = \frac{{x – \alpha }}{a}\]
\[sen\left( t \right) = \frac{{y – \beta }}{b}\]
Análogamente a lo visto para la circunferencia, el parámetro \(t\) debería tomar todos los valores en el intervalo \(\left[ {0,2\pi } \right]\):
Obtuvimos así una parametrización de la elipse con \(C\left( {\alpha ,\beta } \right)\) y semiejes \(a\) y \(b\).
Retomemos la ecuación dada:
\[{x^2} + 4{y^2} – 2x + 4y + 1 = 0\]
Saquemos factor común:
\[{x^2} – 2x + 4\left( {{y^2} + y} \right) + 1 = 0\]
Completemos cuadrados:
\[{\left( {x – 1} \right)^2} – {1^2} + 4\left[ {{{\left( {y + \frac{1}{2}} \right)}^2} – {{\left( {\frac{1}{2}} \right)}^2}} \right] + 1 = 0\]
\[{\left( {x – 1} \right)^2} + 4{\left( {y + \frac{1}{2}} \right)^2} = 1\]
\[{\left( {x – 1} \right)^2} + \frac{{{{\left( {y + \frac{1}{2}} \right)}^2}}}{{\frac{1}{4}}} = 1\]
Esta expresión corresponde a la ecuación canónica de una elipse con centro \(\left( {1, – \frac{1}{2}} \right)\) y semiejes \(a = 1\), \(b = \frac{1}{2}\).
Una posible parametrización es:
\[\left\{ {\begin{array}{*{20}{c}}{x = 1 + \cos \left( t \right)}\\{y = – \frac{1}{2} + \frac{1}{2}sen\left( t \right)}\end{array}\;\;\;} \right.t \in \left[ {0,2\pi } \right]\]
Ejercicio para el lector 6
Dada la ecuación
\[2{x^2} + {y^2} – 8x + 2y – 1 = 0\]
a) Hallar la ecuación canónica de la cónica correspondiente, indicando las coordenadas del centro, vértices y focos. Graficar.
b) Obtener una parametrización indicando punto inicial y sentido del recorrido de la curva.
Parametrización de la parábola
La ecuación canónica de una parábola con vértice \(V\left( {\alpha ,\beta } \right)\), y eje focal horizontal es:
\[{\left( {y – \beta } \right)^2} = 4c\left( {x – \alpha } \right)\]
Si llamamos \(t = y – \beta \) :
\[\left\{ {\begin{array}{*{20}{c}}{x – \alpha = \frac{1}{{4c}}{t^2}}\\{y – \beta = t}\end{array}\;\;} \right.\]
Entonces:
\[\left\{ {\begin{array}{*{20}{c}}{x = \frac{1}{{4c}}{t^2} + \alpha }\\{y = t + \beta }\end{array}} \right.\;\;\;t \in \mathbb{R}\]
Ésta es una parametrización de la parábola de eje focal horizontal con vértice \(V\left( {\alpha ,\beta } \right)\).
En el caso en que la parábola sea de eje focal vertical, resulta:
\[{\left( {x – \alpha } \right)^2} = 4c\left( {y – \beta } \right)\]
\[\left\{ {\begin{array}{*{20}{c}}{x – \alpha = t}\\{y – \beta = \frac{1}{{4c}}{t^2}}\end{array}\;\;\;} \right.\]
\[\left\{ {\begin{array}{*{20}{c}}{x = t + \alpha }\\{y = \frac{1}{{4c}}{t^2} + \beta }\end{array}} \right.\;\;t \in \mathbb{R}\]
Ejemplo 1
Parametrizar el arco de la parábola cuya ecuación es \({y^2} = – 4x\) comprendido entre los puntos \(\left( {0,0} \right)\) y \(\left( { – 9,6} \right)\).
Resolución
Se trata de una parábola con eje focal horizontal. En este caso los valores de \(\alpha \) y \(\beta \) son ambos \(0\). Luego podemos hacer la siguiente parametrización:
\[\left\{ {\begin{array}{*{20}{c}}{x = – \frac{1}{4}{t^2}}\\{y = t}\end{array}\;} \right.\]
Pero debemos definir en qué intervalo real tomará valores el parámetro. El punto \(\left( {0,0} \right)\), ¿a qué valor del parámetro se corresponde? Sustituimos \(x = y = 0\), y despejamos el valor de \(t\)
\[0 = – \frac{1}{4}{t^2}\;\;,\;\;\;0 = t\]
¿Y qué valor toma para el punto \(\left( { – 9,6} \right)\)?
\[\left\{ {\begin{array}{*{20}{c}}{ – 9 = – \frac{1}{4}{t^2} \Rightarrow \left| t \right| = 6}\\{6 = t}\end{array}} \right.\]
Luego el intervalo es:
\[t \in \left[ {0,6} \right]\]
La parametrización definida en forma completa quedaría entonces:
\[\left\{ {\begin{array}{*{20}{c}}{x = – \frac{1}{4}{t^2}}\\{y = t}\end{array}\;\;\;\;t \in \left[ {0,6} \right]} \right.\]
En el siguiente archivo de GeoGebra se puede corroborar como para cada valor del parámetro tenemos un punto en el plano correspondiente al arco de parábola:
Ejemplo 2
Parametrizar la curva definida por:
\({y^2} + 4x + 2y – 3 = 0\) , \(x \ge 0\)
Resolución
Cómo aparece la variable \(y\) elevada al cuadrado y no aparece la variable \(x\) elevada al cuadrado, podemos suponer inicialmente que se tratará de una parábola. Completemos cuadrados para llegar a su ecuación ordinaria:
\[{y^2} + 2y = – 4x + 3\]
\[{\left( {y + 1} \right)^2} – 1 = – 4x + 3\]
\[{\left( {y + 1} \right)^2} = – 4x + 4\]
\[{\left( {y + 1} \right)^2} = – 4\left( {x – 1} \right)\]
Ésta es la ecuación de una parábola de eje focal horizontal (porque es \(y\) la variable que aparece elevada al cuadrado) con vértice en \(\left( {1, – 1} \right)\). ¿Las «ramas» de esta parábola apuntarán hacia derecha o izquierda? Hacia izquierda, esto podemos verlo en que \(x\) debe tomar valores que no hagan negativo el segundo miembro. Es decir:
\[ – 4\left( {x – 1} \right) \ge 0 \Rightarrow \;x – 1 \le 0 \Rightarrow \;x \le 1\]
Grafiquemos el vértice e imaginemos a las «ramas» de la parábola hacia la izquierda:
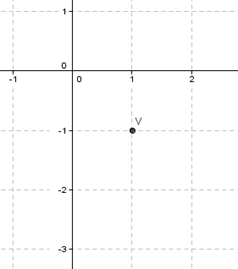
Cortará al eje \(y\) en dos puntos, que no sabemos cuáles son. Además como se pide que \(x \ge 0\) no tenemos la parábola completa sino sólo un arco de ella. Para saber cuál será ese arco busquemos los valores que toma \(y\) cuando \(x = 0\)
\[{\left( {y + 1} \right)^2} = – 4\left( {0 – 1} \right) \Rightarrow \;{\left( {y + 1} \right)^2} = 4 \Rightarrow \left| {y + 1} \right| = 2 \Rightarrow y = 1\; \vee \;y = – 3\]
Luego ya podemos graficar la parábola y destacar cual es el arco que queremos parametrizar:
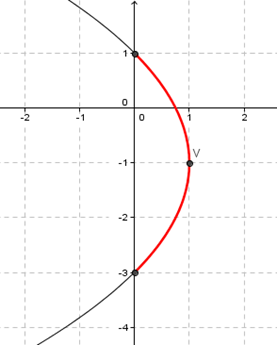
Una parametrización de la parábola podría hacerse igualando al parámetro con \(y + 1\):
\[\left\{ {\begin{array}{*{20}{c}}{t = y + 1}\\{{t^2} = – 4\left( {x – 1} \right)}\end{array}\; \Rightarrow \;\;\;\left\{ {\begin{array}{*{20}{c}}{y = t – 1}\\{x = – \frac{{{t^2}}}{4} + 1}\end{array}} \right.} \right.\;\;\;\;t \in \mathbb{R}\;\]
Cómo sólo queremos que los valores de \(y\) varíen entre \( – 3\) y \(1\), entonces:
Y finalmente la parametrización del arco de parábola es:
\[\left\{ {\begin{array}{*{20}{c}}{y = t – 1}\\{x = – \frac{{{t^2}}}{4} + 1}\end{array}} \right.\;\;t \in \left[ { – 2,2} \right]\]
A continuación se puede ver en GeoGebra como para cada valor del parámetro obtenemos un punto sobre el arco de parábola:
Ejercicio para el lector 7
a) Hallar la ecuación de la parábola con directriz \(y = – 1\) y foco \(F\left( {1,3} \right)\)
b) Parametrizar el arco de parábola que verifica la restricción: \(y \le 9\).
«Desparametrización» de una parábola
En un tiro oblicuo al descomponer el movimiento del proyectil según la dirección horizontal (MRU) y vertical (MRUV) queda establecida la siguiente parametrización:
\[\left\{ {\begin{array}{*{20}{c}}{x = {v_{0x}}t}\\{y = {v_{0y}}.t – \frac{1}{2}g{t^2}}\end{array}} \right.\]
Si \(t\) en estas ecuaciones representa al tiempo, ¿cuál sería el intervalo de parametrización?
Para obtener la trayectoria del proyectil, eliminamos el parámetro de las ecuaciones:
\[t = \frac{x}{{{v_{0x}}}}\;\; \Rightarrow \;\;y = {v_{0y}}\frac{x}{{{v_{0x}}}} – \frac{1}{2}g{\left( {\frac{x}{{{v_{0x}}}}} \right)^2} = \left( {\frac{{{v_{0y}}}}{{{v_{0x}}}}} \right)x – \left( {\frac{g}{{2{v_{0x}}^2}}} \right).{x^2}\]
Se obtiene una función cuadrática, es decir que la trayectoria es parabólica.
Ejemplo
Hallar la ecuación cartesiana y graficar la curva de ecuaciones paramétricas:
\[\left\{ {\begin{array}{*{20}{c}}{x = 1 + t}\\{y = 2 – {t^2}}\end{array}\;\;\;t \in \left[ { – \sqrt 2 ;\sqrt 2 } \right]} \right.\]
Resolución
Para obtener la ecuación cartesiana despejamos el parámetro \(t\) de la primera ecuación y luego lo sustituimos en la segunda:
\[t = x – 1\]
\[y = 2 – {\left( {x – 1} \right)^2}\]
Es una parábola cuyas ramas apuntan hacia abajo, y vértice en \(\left( {1,2} \right)\):
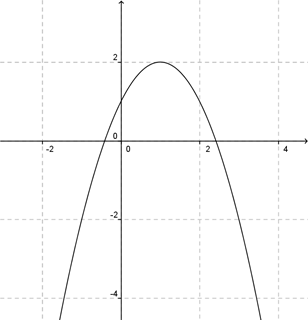
Pero no queremos graficar la parábola entera, sino sólo el arco definido por la parametrización. Consideremos que puntos corresponden a los valores extremos del intervalo:
\[Cuando\;t = – \sqrt 2 \to P\left( {1 – \sqrt 2 ,0} \right)\]
\[Cuando\;t = \sqrt 2 \to P\left( {1 + \sqrt 2 ,0} \right)\]
Estos dos puntos son las raíces porque la ordenada es 0. Entonces el arco de parábola va desde \(\left( {1 – \sqrt 2 ,0} \right)\) hasta \(\left( {1 + \sqrt 2 ,0} \right)\). Lo mostramos en la gráfica en color rojo:
Parametrización de la hipérbola
Cuando parametrizamos la circunferencia y la elipse utilizamos la relación pitagórica: \(se{n^2}\left( t \right) + {\cos ^2}\left( t \right) = 1\). Esta relación no nos sirve en el caso de la hipérbola, pero podemos utilizar otra identidad trigonométrica:
\({\sec ^2}\left( t \right) – t{g^2}\left( t \right) = 1\)
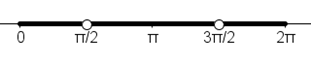
Observación: si consideramos el intervalo \(\left[ {0,2\pi } \right]\) las funciones \(\sec \left( t \right)\) y \(tg\left( t \right)\) no están definidas ni en \(t = \frac{\pi }{2}\) ni en \(t = \frac{3}{2}\pi \).
Consideremos la ecuación canónica de una hipérbola de eje focal \(x\):
\[\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\]
Es posible escribirla como una diferencia de cuadrados y utilizar la identidad trigonométrica recién presentada:
Entonces resulta:
Que es la parametrización de la hipérbola con centro \(C\left( {0.0} \right)\) y eje focal \(y = 0\) (eje \(x)\).
Observación: el conjunto de valores del parámetro puede expresarse también así:
\[\left[ {0,2\pi } \right] – \left\{ {\frac{\pi }{2},\frac{3}{2}\pi } \right\} = \left[ {0,\frac{\pi }{2}} \right) \cup \left( {\frac{\pi }{2},\frac{{3\pi }}{2}} \right) \cup \left( {\frac{{3\pi }}{2},2\pi } \right]\]
En el caso de la hipérbola de eje focal \(x = 0\;\) (eje \(y\)), se opera de forma análoga:
\[\frac{{{y^2}}}{{{a^2}}} – \frac{{{x^2}}}{{{b^2}}} = 1\]
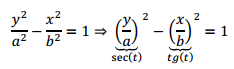
Ejemplo
Hallar una parametrización de la hipérbola definida por la siguiente ecuación.
\[\frac{{{x^2}}}{4} – {y^2} = 1\]
Resolución
Se trata de una hipérbola de eje focal \(x\). Así que siguiendo la parametrización realizada para el caso general podemos llegar a:
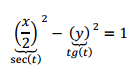
Entonces:
\[\left\{ {\begin{array}{*{20}{c}}{x = 2.\sec \left( t \right)}\\{y = tg\left( t \right)}\end{array}} \right.\;\;t \in \left[ {0,2\pi } \right] – \left\{ {\frac{\pi }{2},\frac{3}{2}\pi } \right\}\;\]
Ésta es una parametrización de la hipérbola dada. A continuación se puede ver en GeoGebra que para cada valor del parámetro se define un punto sobre la curva:
Nótese en el applet que cuando
-
- \(t \in \left[ {0,\frac{\pi }{2}} \right)\) se obtienen puntos de la hipérbola en el primer cuadrante
- \(t \in \left( {\frac{\pi }{2},\frac{{3\pi }}{2}} \right)\) se obtienen puntos de la hipérbola en el tercer y segundo cuadrante
-
\(t \in \left( {\frac{{3\pi }}{2},2\pi } \right]\) se obtienen puntos de la hipérbola en el cuarto cuadrante
Videos relacionados con parametrización de cónicas

