Deducción de la ecuación general del plano
Dada una dirección en \({\mathbb{R}^3}\), existen infinitos planos perpendiculares a la misma. Si conocemos además un punto del plano, éste queda determinado de forma única.
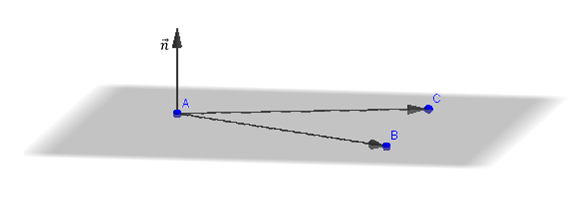
Nos proponemos hallar la ecuación del plano \(\pi \) que pasa por \({P_0}\left( {{x_0},{y_0},{z_0}} \right)\) y es perpendicular al vector \(\vec n = \left( {a,b,c} \right).\) El vector \(\vec n\) se denomina vector normal del plano.
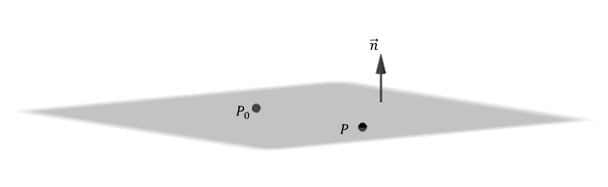
¿Qué condición debe cumplir un punto \(P\left( {x,y,z} \right)\) para estar en el plano \(\pi \)? Si armamos el vector \(\overrightarrow {\;{P_0}P} \;\), éste debe ser paralelo al plano, o sea perpendicular al vector normal del plano:
\[P\left( {x,y,z} \right) \in \pi \; \Leftrightarrow \overrightarrow {\;{P_0}P} \bot \vec n\;\; \Leftrightarrow \;\;\overrightarrow {{P_0}P} .\vec n = 0\]
\[\left( {x – {x_{0\;}},\;y – {y_0},\;z – {z_0}} \right).\left( {a,b,c} \right) = 0\]
\[a\left( {x – {x_0}} \right) + b\left( {y – {y_0}} \right) + c\left( {z – {z_0}} \right) = 0\]
![]()
Ejemplo
Hallar la ecuación del plano perpendicular al vector \(\vec n = \left( {3,2,1} \right)\) que pasa por el punto \({P_0}\left( {1,1, – 1} \right)\).
Las componentes de \(\vec n\) nos indican los coeficientes \(a\), \(b\) y \(c\) de la ecuación del plano:
\[\pi :\;\;3x + 2y + z + d = 0\]
¿Cómo hallamos \(d\)?
El punto debe verificar la ecuación, entonces reemplazamos \({P_0}\) y obtenemos el coeficiente que faltaba:
\[3.1 + 2.1 – 1 + d = 0\; \Rightarrow d = – 4\]
Así obtenemos la ecuación del plano:
\[\pi :\;\;3x + 2y + z – 4 = 0\]
Éste es el único plano que pasa por el punto \({P_0}\;\;\)y es perpendicular al vector \(\vec n\).
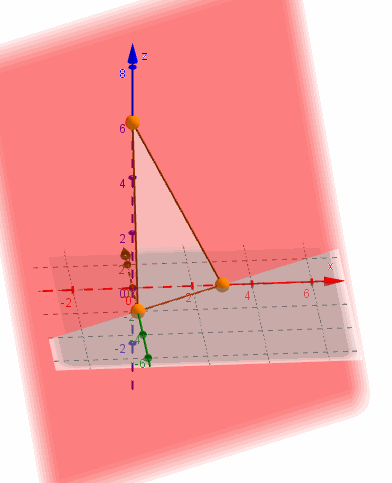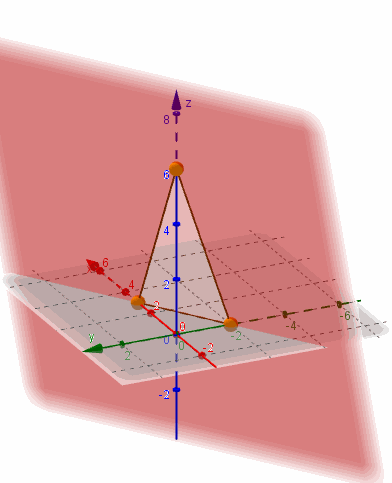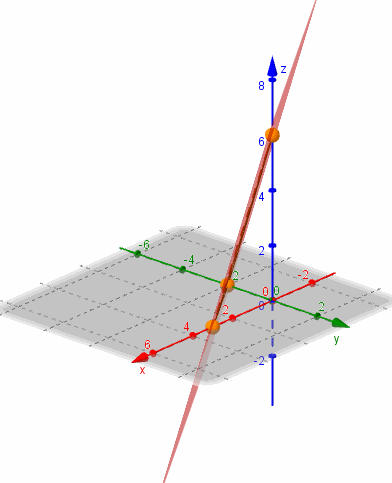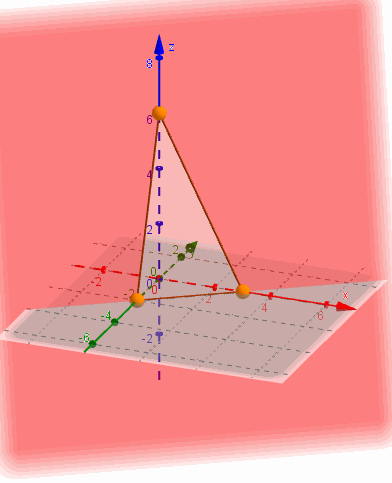
Para efectuar un gráfico aproximado del plano que obtuvimos, podemos buscar sus intersecciones con los ejes coordenados:
Para hallar la intersección con el eje \(x\), debemos plantear \(y = z = 0\) y despejar el valor de \(x\). Análogamente para las otras intersecciones, tal como se muestra en el siguiente cuadro:

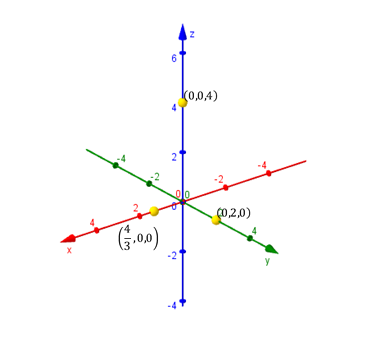
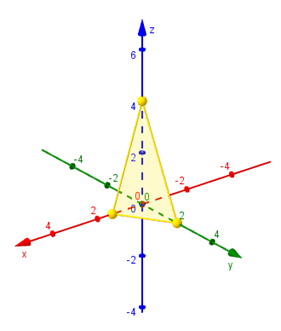
Tres puntos no alineados determinan un único plano que los contiene. Trazamos los segmentos que unen los puntos hallados y obtenemos la representación gráfica de una porción del plano:
Mostramos una gráfica del plano realizada con GeoGebra:
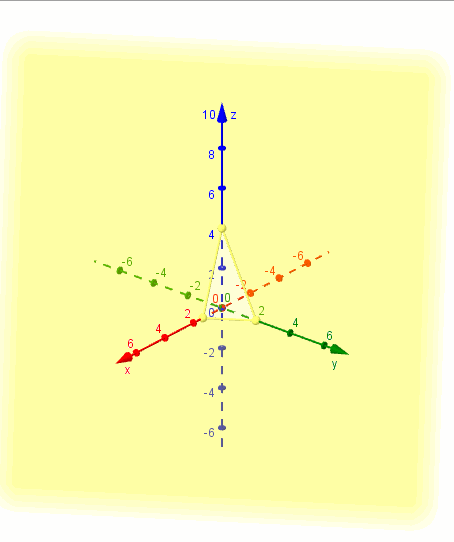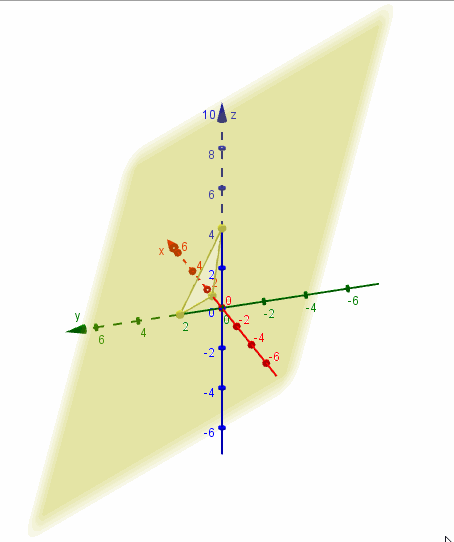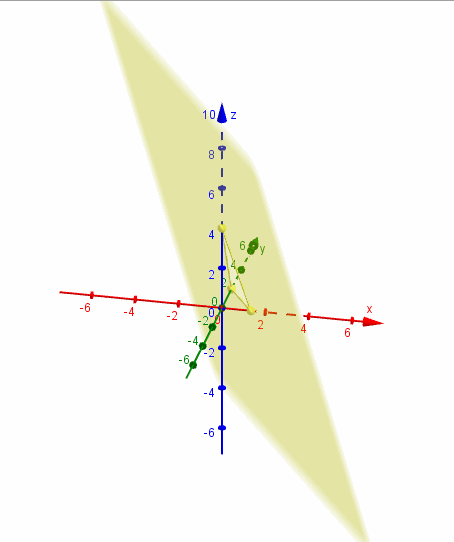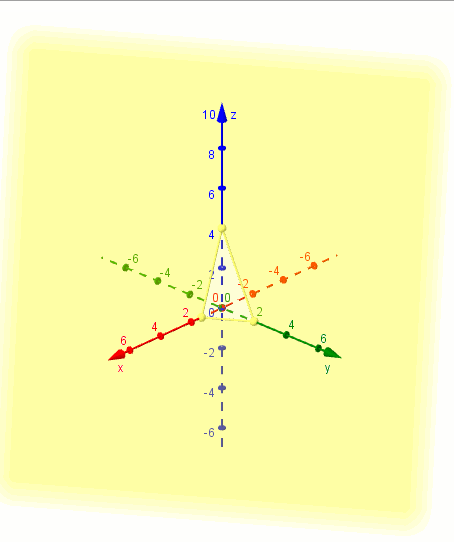
Ejemplo
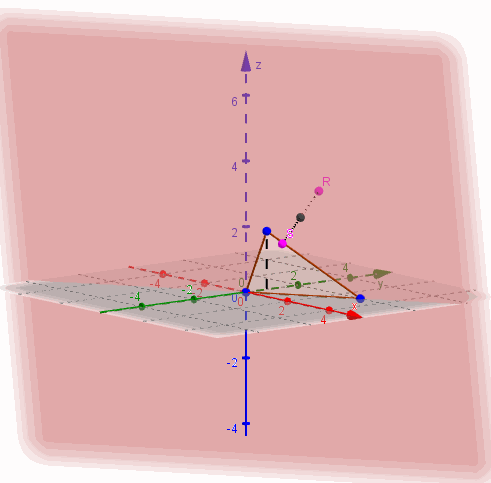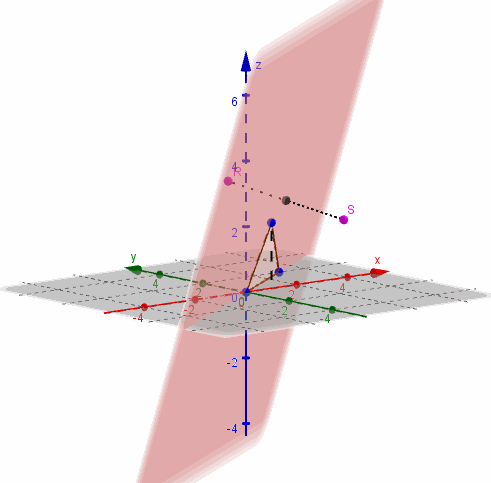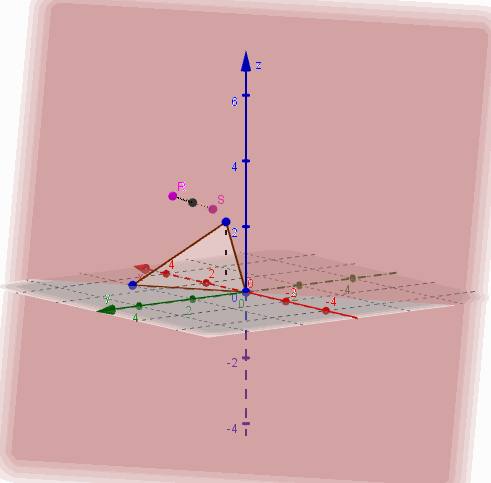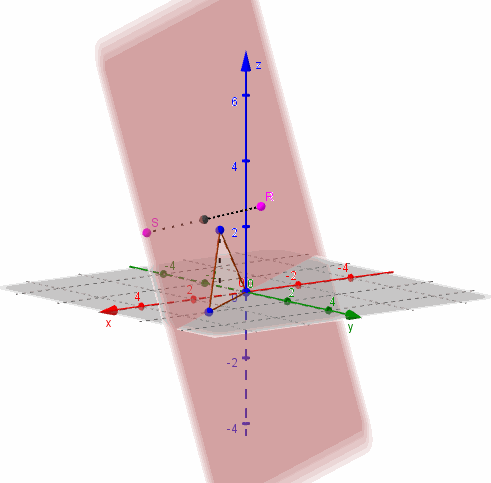
Dados los puntos \(R\left( {1,2,3} \right)\) y \(S\left( {3, – 1,2} \right)\), encontrar la ecuación del plano que corta perpendicularmente al segmento \(RS\) en su punto medio.
Resolución
Busquemos las coordenadas del punto medio:
\[M = \left( {\frac{{1 + 3}}{2},\frac{{2 + \left( { – 1} \right)}}{2},\frac{{3 + 2}}{2}} \right) = \left( {2,\frac{1}{2},\frac{5}{2}} \right)\]
Como el plano corta perpendicularmente al segmento \(RS\), podemos tomar \(\overrightarrow {RS} \;\;\)como vector normal del plano:
\[\overrightarrow {RS} = \left( {2, – 3, – 1} \right)\]
Escribimos la ecuación del plano al que llamaremos \(\beta \):
\[\beta :\;\;\;2x – 3y – 1z + d = 0\]
Para hallar \(d\) reemplazamos el punto \(M\):
\[2.2 – 3.\frac{1}{2} – \frac{5}{2} + d = 0\; \Rightarrow d = 0\]
Y así obtenemos la ecuación buscada:
\[\beta :\;\;\;2x – 3y – z = 0\]
Este plano pasa por el origen, o sea que interseca a los tres ejes en \(\left( {0,0,0} \right)\). Necesitamos al menos dos puntos más para graficarlo.
Para facilitar el gráfico podemos elegir puntos que estén sobre los planos coordenados. Por ejemplo \(y = 0\;\):
\[\; \Rightarrow 2x – z = 0 \Rightarrow z = 2x\]
Entonces haciendo que \(x = 1\) debe ser \(z = 2\), y obtenemos el punto \({P_1}\left( {1,0,2} \right)\)
Para tomar otro punto del plano podemos hacer que \(z = 0\)
\[\; \Rightarrow \;2x – 3y = 0 \Rightarrow y = \frac{2}{3}x\]
Y si \(x = 3\) entonces \(y = 2\). Obtenemos el punto \({P_2}\left( {3,2,0} \right)\)
Entonces \(\beta \) contiene a los puntos \(\left( {0,0,0} \right)\;,\;\left( {1,0,2} \right)\) y \(\left( {3,2,0} \right)\):
Ejemplo
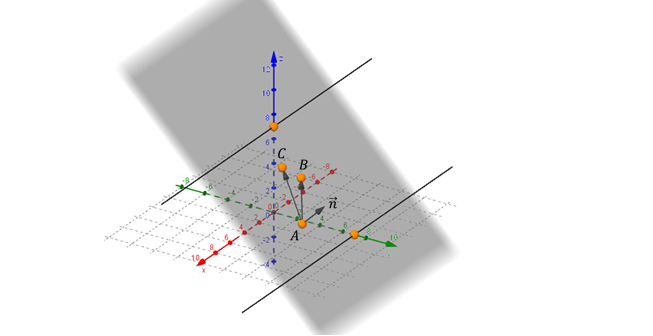
Dados \(A\left( {4,5,2} \right),\;\;B\left( {1,3,4} \right)\), \(C\left( {2,2,5} \right)\) hallar, si es posible, el plano que contiene a los tres puntos.
Habíamos dicho que tres puntos no alineados determinan un único plano que los contiene.
Hagamos una figura de análisis:
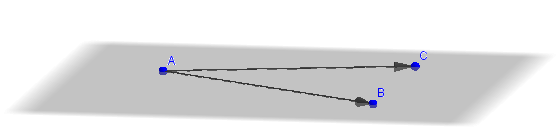
Con los tres puntos, podemos armar dos vectores, por ejemplo:
\[\overrightarrow {AB} = \left( { – 3, – 2,2} \right)\]
\[\overrightarrow {AC} = \left( { – 2, – 3,3} \right)\]
El vector normal debe ser perpendicular a ambos vectores cómo muestra la siguiente figura:
¿Qué operación nos permite hallar un vector perpendicular a otros dos?
\[(\overrightarrow {AB} \times \overrightarrow {AC} = \left( {0,5,5} \right)\]
¿Qué resultado habríamos obtenido si \(A\), \(B\) y \(C\) estuvieran alineados?
El vector \(\left( {0,5,5} \right)\) es perpendicular al plano que buscamos, entonces podemos tomar \(\vec n\;\; = \;\left( {0,5,5} \right)\) y escribir la ecuación del plano:
\[\alpha :\;\;\;5y + 5z + d = 0\]
Para hallar \(d\) podemos reemplazar cualquiera de los tres puntos. Reemplacemos \(A\):
\[5.5 + 5.2 + d = 0 \Rightarrow d = – 35\]
Luego:
\[5y + 5z – 35 = 0\]
Podemos dividir por 5 ambos miembros:
\[\alpha :\;\;\;y + z – 7 = 0\]
El lector puede comprobar que los puntos \(B\) y \(C\) verifican esta ecuación.
Busquemos las intersecciones con los ejes para graficar el plano:
\[y = z = 0 \Rightarrow – 7 = 0\;\;\;Absurdo\]
Entonces \(\alpha \) no corta al eje \(x\).
¿En qué punto corta al eje \(y\)? \(\;\left( {0,7,0} \right)\)
¿Y al eje \(z\)? \(\left( {0,0,7} \right)\)
Observemos que el plano contiene a todos los puntos de la forma \(\left( {x,7,0} \right)\) con \(x \in \mathbb{R}.\)
Lo mismo ocurre con los puntos del tipo \(\left( {x,0,7} \right)\) con \(x \in \mathbb{R}.\)
Podemos observar entonces que:
\[\;a = 0 \Rightarrow el\;plano\;es\parallel \;\;al\;eje\;x\]
Ecuación segmentaria del plano
Dada la ecuación general de un plano:
\[\pi :\;\;ax + by + cz + d = 0\]
Si \(a,b,c,d\) son distintos de cero, es posible obtener otra ecuación del plano como sigue:
\[ax + by + cz = – d\]
\[\frac{a}{{ – d}}x + \frac{b}{{ – d}}y + \frac{c}{{ – d}}z = 1\]
\[\frac{x}{{\left( { – \frac{d}{a}} \right)}} + \frac{y}{{\left( { – \frac{d}{b}} \right)}} + \frac{z}{{\left( { – \frac{d}{c}} \right)}} = 1\]
Si llamamos \(p = – \frac{d}{a}\) , \(q = – \frac{d}{b}\), \(r = – \frac{d}{c}\)
Resulta:
Veamos qué indican \(p\), \(q\) y \(r\):
¿Cuál es la intersección del plano con el eje x?![]()
¿Cuál es la intersección con el eje y?
\[\left( {0,q,0} \right)\]
¿Y con el eje z?
\[\left( {0,0,r} \right)\]
Podemos observar que p, q y r indican las intersecciones con los ejes.
Ejemplo
\[2x – 3y + z – 6 = 0\]
\[2x – 3y + z = 6\]
\[\frac{{2x}}{6} – \frac{{3y}}{6} + \frac{z}{6} = 1\]
\[\frac{x}{3} – \frac{y}{2} + \frac{z}{6} = 1\]
Esta ecuación parece segmentaria pero no lo es por el signo negativo. La reescribimos así:
\[\frac{x}{3} + \frac{y}{{ – 2}} + \frac{z}{6} = 1\;\;\;\;\;\;\;Ecuación\;segmentaria\]
La ecuación segmentaria es práctica para graficar un plano porque muestra los tres puntos de corte con los ejes:
Ecuación vectorial paramétrica del plano
Dados dos vectores \(\vec u = \left( {{u_1},{u_2},{u_3}} \right)\) y \(\overrightarrow {v\;} = \left( {{v_1},\;{v_2},\;{v_3}} \right)\) no paralelos y un punto \({P_0}\;\left( {{x_0},\;{y_0},\;{z_0}} \right)\), nos proponemos hallar la ecuación del plano \(\pi \) que pasa por \({P_0}\)
y es paralelo a \(\overrightarrow {\;u} \) y \(\overrightarrow {v\;} \).
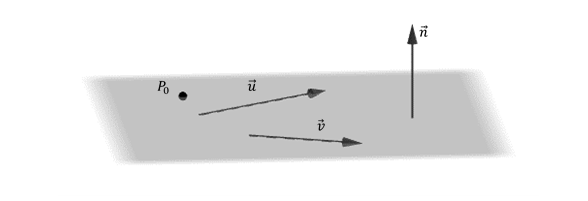
¿Cómo podemos obtener un vector perpendicular al plano conociendo dos vectores paralelos a dicho plano?
\[\vec n = \vec u \times \vec v\]
Teniendo \(\vec n\;\) y el punto \({P_0}\), podemos hallar la ecuación implícita o general del plano \(\pi \) como habíamos visto previamente.
Obtendremos a continuación otro tipo de ecuación del plano, cuya deducción se basa en el concepto de combinación lineal de vectores, tal cómo vimos en el ejemplo.
Si \(P\left( {x,y,z} \right)\) es un punto cualquiera del plano \(\pi \), los vectores \(\overrightarrow {{P_0}P} \;,\;\vec u\;\;y\;\;\;\vec v\;\) son coplanares
Entonces
\[\exists \alpha ,\beta \in \mathbb{R}\;\;|\;\;\overrightarrow {{P_0}P} = \alpha \;\vec u + \beta \;\vec v\]
Esto significa que el vector \(\overrightarrow {{P_0}P} \) puede expresarse como combinación lineal de \(\vec u\) y \(\vec v\), como se muestra en la figura:
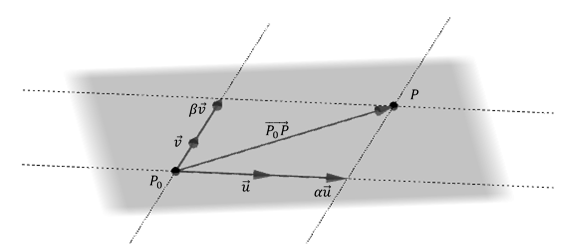
\[\left( {x – {x_0}\;,\;y – {y_0},z – {z_0}} \right) = \alpha .\left( {{u_1},{u_2},{u_3}} \right)\; + \beta \;\left( {{v_1},{v_2},{v_3}} \right)\]
Por lo tanto:
\(\left( {x,y,z} \right) = \left( {{x_0},{y_0},{z_0}} \right) + \alpha \;\left( {{u_1},{u_2},{u_3}} \right) + \beta \;\left( {{v_1},{v_2},{v_3}} \right)\),\(\;\;con\;\alpha ,\beta \in \mathbb{R}\)
O en notación vectorial:
Ejemplo
Armar la ecuación vectorial paramétrica del plano paralelo a \(\vec u = \left( {3, – 1,5} \right)\) y \(\vec v = \left( {7,3,2} \right)\) que pasa por el punto \({P_0}\left( {0, – 1,8} \right).\)
De acuerdo con lo que hemos visto, tenemos toda la información para escribir la ecuación vectorial paramétrica:
\[\left( {x,y,z} \right) = \left( {0, – 1,8} \right) + \alpha \left( {3, – 1,5} \right) + \beta \left( {7,3,2} \right)\;\;,\;\;\;con\;\alpha ,\beta \in \mathbb{R}\]
Nota: Para cada \(\alpha \;y\;\beta \in \mathbb{R}\) se obtiene un punto del plano. Por ejemplo si \(\;\alpha = 1\;\;y\;\;\;\beta = – 1\) se obtiene el punto \(\left( {x,y,z} \right) = \left( { – 4,\; – 5,\;11} \right)\).
Busquemos ahora la ecuación general de este plano.
\[\vec n = \vec u \times \vec v = \left( {3, – 1,5} \right) \times \left( {7,3,2} \right) = \left( { – 17,\;29,16} \right)\]
Luego:
\[ – 17x + 29y + 16z + d = 0\]
Reemplazamos \({P_0}\) para obtener \(d\):
\[ – 17.0 + 29.\left( { – 1} \right) + 16.8 + d = 0 \Rightarrow \;d = – 99\]
Luego:
\[ – 17x + 29y + 16z – 99 = 0\]
que es la ecuación general o implícita del plano.
De la ecuación general a la ecuación vectorial paramétrica
Dada la ecuación general de un plano, ¿cómo puede obtenerse una ecuación vectorial paramétrica de dicho plano?
Consideremos el siguiente ejemplo:
\[\omega :\;\;\;2x – y + 3z + 9 = 0\]
Podemos despejar cualquiera de las variables, por ejemplo y:
\[y = 2x + 3z + 9\]
Entonces:
\[\omega :\;\;\;\left( {x,y,z} \right) = \left( {x,\;2x + 3z + 9\;,z} \right)\;\;\]
Reescribimos como suma de tres vectores, de forma tal que uno de ellos tenga los términos con \(x\), otro los términos con \(z\) y otro los términos independientes:
\[\left( {x,y,z} \right) = \left( {x,2x,0} \right) + \left( {0,3z,z} \right) + \left( {0,9,0} \right)\;\]
\[\left( {x,y,z} \right) = x\left( {1,2,0} \right) + z\left( {0,3,1} \right) + \left( {0,9,0} \right)\;,\;con\;\;x,z \in R\;\]
Si llamamos \(x = \alpha \) , \(z = \beta \), resulta:
\[\omega :\;\;\;\left( {x,y,z} \right) = \left( {0,9,0} \right) + \alpha \left( {1,2,0} \right) + \beta \left( {0,3,1} \right)\;,\;con\;\;\alpha ,\beta \in R\;\;\]
Obtuvimos así una ecuación vectorial paramétrica del plano \(\omega .\)
El lector puede comprobar que: i) los vectores \(\vec u\) = (1,2,0) y \(\vec v\) = (0,3,1) son perpendiculares a \(\vec n\) = (2,-1,3), o sea que son paralelos al plano; ii) P0(0,9,0) \( \in \omega \).
Videos relacionados con ecuación del plano

