Enunciado del primer parcial de álgebra [05-05-2018]

Ejercicio 1 – Recta y plano
Sean las rectas \({t_1}:\left\{ {\begin{array}{*{20}{c}}{2x – y = 0}\\{x + 3y + z + \beta = 0}\end{array}} \right.\) y \({t_2}:\;\;x – 1 = y – 3 = z\)
a) Obtenga \(\beta \in \mathbb{R}\) sabiendo que \({t_1}\) y \({t_2}\) son coplanares
b) Proporcione la ecuación general del plano determinado por las rectas dadas.
Resolución del ejercicio 1
Ítem a
Recordemos que la condición de coplanaridad entre dos rectas es:
\[\overrightarrow {{v_1}} \times \overrightarrow {{v_2}} \left( {\overrightarrow {{P_1}{P_2}} } \right) = 0\]
Siendo \({v_1}\) el vector director de la recta 1, \({v_2}\) el vector director de la recta 2, y \({P_1}\) y \({P_2}\) puntos de las rectas 1 y 2 respectivamente.
Entonces vamos a:
(1) Hallar \(\overrightarrow {{v_1}} \),\(\overrightarrow {{v_2}} \) \({P_1}\) y \({P_2}\)
(2) Plantear la condición de coplanaridad
(3) Despejar el valor de \(\beta \)
Cómo \({t_1}:\left\{ {\begin{array}{*{20}{c}}{2x – y = 0}\\{x + 3y + z + \beta = 0}\end{array}} \right.\) está dada cómo intersección de dos planos, es posible obtener el vector director de \({t_1}\) haciendo el producto vectorial entre los vectores normales de esos planos:
\[\overrightarrow {{v_1}} = \left| {\begin{array}{*{20}{c}}2&{ – 1}&0\\1&3&1\end{array}} \right| = \left( { – 1, – 2,7} \right)\]
Para obtener un punto \({P_1} \in {t_1}\) podemos dar un valor arbitrario a \(x\), y averiguar los valores de \(y\) y de \(z\). Por ejemplo:
\[x = 0 \Rightarrow \left\{ {\begin{array}{*{20}{c}}{2.0 – y = 0}\\{0 + 3y + z + \beta = 0}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{y = 0}\\{z = – \beta }\end{array}} \right.\]
\[ \Rightarrow {P_1} = \left( {0,0, – \beta } \right)\]
La recta \({t_2}\) está dada en forma simétrica. Entonces el vector director lo podemos sacar directamente:
\[{t_2}:\;x – 1 = y – 3 = z\]
\[\overrightarrow {{v_2}} = \left( {1,1,1} \right)\]
Un punto de paso puede obtenerse buscando los valores de \(x\), de \(y\) y de \(z\) que anulan cada miembro:
\[x – 1 = 0 \Rightarrow x = 1\]
\[y – 3 = 0 \Rightarrow y = 3\]
\[z = 0\]
\[ \Rightarrow {P_2} = \left( {1,3,0} \right)\]
Ahora podemos obtener \(\overrightarrow {{P_1}{P_2}} \):
\[\overrightarrow {{P_1}{P_2}} = \left( {1,3,0} \right) – \left( {0,0, – \beta } \right) = \left( {1,3,\beta } \right)\]
Ya podemos plantear el producto mixto:
\[\overrightarrow {{v_1}} \times \overrightarrow {{v_2}} \left( {\overrightarrow {{P_1}{P_2}} } \right) = 0\]
\[\overrightarrow {{v_1}} \times \overrightarrow {{v_2}} = \left| {\begin{array}{*{20}{c}}{ – 1}&{ – 2}&7\\1&1&1\end{array}} \right| = \left( { – 9,8,1} \right)\]
\[ \Rightarrow \left( { – 9,8,1} \right)\left( {1,3,\beta } \right) = – 9 + 24 + \beta = 0\]
\[ \bbox[yellow,5px]
{
\Rightarrow \beta = – 15
}
\]
Ítem b
El producto vectorial de los vectores directores de las dos rectas es igual al vector normal del plano que las contiene. (Cuando las rectas no son paralelas).
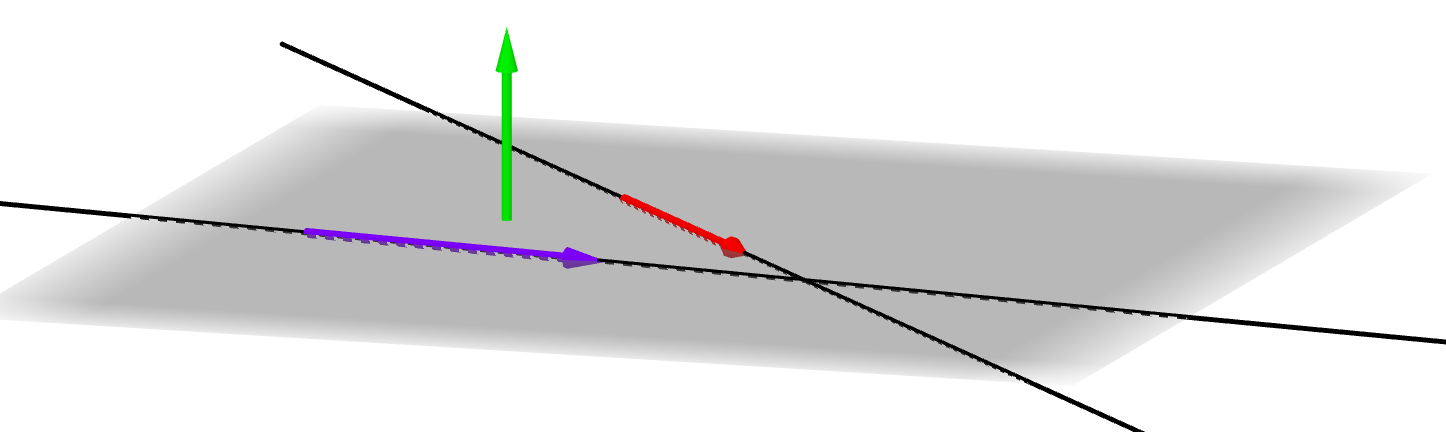
Entonces:
\[\pi : – 9x + 8y + z + d = 0\]
Sabemos que \(\left( {1,3,0} \right) \in \pi \):
\[ – 9.1 + 8.3 + 0 + d = 0 \Rightarrow d = – 15\]
\[ \bbox[yellow,5px]
{
\Rightarrow \pi :\; – 9x + 8y + z – 15 = 0
}
\]
Ejercicio 2 – Haz de planos
Dada la recta \(r:\left\{ {\begin{array}{*{20}{c}}{x – 2y = 0}\\{x + z = k}\end{array}} \right.\) y el haz de planos \(2x + y + z – 5 + \alpha \left( { – x + 2y – 3z – 5} \right) = 0\)
a) Halle el plano del haz que es paralelo a \(r\)
b) Determine los valores de \(k \in \mathbb{R}\) para los cuales la recta \(r\) está incluida en el plano hallado.
Resolución del ejercicio 2
Ítem a
Tenemos que hallar un plano \(\pi \) del haz de planos que sea paralelo a \(r\).
Veamos en un diagrama cómo es un plano paralelo a una recta:
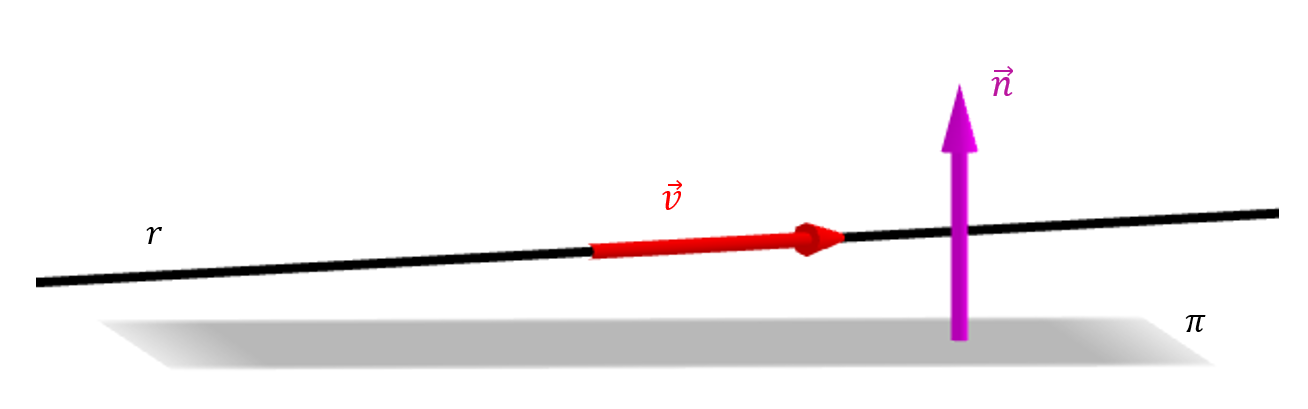
Un plano es paralelo a una recta si el vector normal del plano \( \color{fuchsia}{\vec n}\) es perpendicular al vector director de la recta \(\color{red}{\vec v}\).
Así que vamos a plantear \(\vec v.\vec n = 0\), para obtener el plano \(\pi \).
La recta \(r:\left\{ {\begin{array}{*{20}{c}}{x – 2y = 0}\\{x + z = k}\end{array}} \right.\) está definida cómo intersección de dos planos, entonces buscando el producto vectorial de los normales a esos planos obtenemos el vector director de la recta:
\[\overrightarrow {{v_r}} = \left| {\begin{array}{*{20}{c}}1&{ – 2}&0\\1&0&1\end{array}} \right| = \left( { – 2, – 1,2} \right)\]
Para obtener un punto de la recta \({P_r}\) podemos asignar un valor arbitrario a \(x\) (también sería válido con \(y\) o con \(z\)). Por ejemplo \(x = 0\):
\[x = 0 \Rightarrow \;\;\;\left\{ {\begin{array}{*{20}{c}}{0 – 2y = 0}\\{0 + z = k}\end{array}} \right.\; \Rightarrow \;\left\{ {\begin{array}{*{20}{c}}{y = 0}\\{z = k}\end{array}} \right.\]
\[ \Rightarrow {P_r} = \left( {0,0,k} \right)\]
Entonces la ecuación vectorial de la recta \(r\) es:
\[r:\lambda \left( { – 2, – 1,2} \right) + \left( {0,0,k} \right)\]
La ecuación del haz de planos es:
\[2x + y + z – 5 + \alpha \left( { – x + 2y – 3z – 5} \right) = 0\]
Distribuyendo y sacando factor común podemos ver la forma de un vector normal del plano:
\[\left( {2 – \alpha } \right)x + \left( {1 + 2\alpha } \right)y + \left( {1 – 3\alpha } \right)z + \left( { – 5 – 5\alpha } \right) = 0\]
\[\vec n = \left( {2 – \alpha ,1 + 2\alpha ,1 – 3\alpha } \right)\]
Planteamos \(\vec v.\vec n = 0\):
\[\left( { – 2, – 1,2} \right)\left( {2 – \alpha ,1 + 2\alpha ,1 – 3\alpha } \right) = 0\]
\[ \Rightarrow – 4 + 2\alpha – 1 – 2\alpha + 2 – 6\alpha = 0\]
\[ \Rightarrow – 6\alpha – 3 = 0\]
\[ \Rightarrow \alpha = – \frac{1}{2}\]
Reemplazando \(\alpha = – \frac{1}{2}\) en la ecuación del haz de planos:
\[ \bbox[yellow,5px]
{
\pi :\;2,5x + 2,5z – 2,5 = 0
}
\]
Item b
Si la recta \(r\) está incluida en el plano, en particular el punto \(\left( {0,0,k} \right)\) debe pertenecer al plano.
Entonces:
\[2,5.0 + 2,5.k – 2,5 = 0\]
\[ \bbox[yellow,5px]
{
\Rightarrow k = 1
}
\]
Ejercicio 3 – Determinantes y subespacios
Justificando en cada caso, determine la verdad o falsedad de:
a) Si \(A = \left( {{A_1}\;\;\;{A_2}\;\;\;{A_3}} \right) \in {\mathbb{R}^{3 \times 3}}\), \(\left| A \right| = – 3\) y \(B = \left( {{A_1}\;\;\;\;\;{A_2} – 2{A_3}\;\;\;\;\;\;{A_2}} \right)\) entonces \(\left| {\frac{1}{3}{A^2}{B^t}{A^{ – 1}}} \right| = 6\)
b) Si \(B = \left\{ {\left( {1, – 1} \right),\left( {1,1} \right)} \right\}\) es base de \({\mathbb{R}^2} \Rightarrow \;\) las coordenadas de \(\left( {5,1} \right)\) en la base \(B\) son \(\left( {\begin{array}{*{20}{c}}2\\3\end{array}} \right)\).
Resolución del ejercicio 3
Ítem a
Aplicando propiedades podemos hallar el determinante de \(B\):

Ahora calculamos el determinante de \(\frac{1}{3}{A^2}.{B^t}.{A^{ – 1}}\) usando propiedades:

Es decir que la afirmación es falsa.
Ítem b
Afirman que \(\left( {\begin{array}{*{20}{c}}2\\3\end{array}} \right)\) son las coordenadas de \(\left( {5,1} \right)\) en la base \(B = \left\{ {\left( {1, – 1} \right),\left( {1,1} \right)} \right\}\).
Si eso fuera verdad entonces debería cumplirse que:
\[\left( {5,1} \right) = 2.\left( {1, – 1} \right) + 3\left( {1,1} \right)\]
\[\left( {5,1} \right) = \left( {2, – 2} \right) + \left( {3,3} \right)\]
\[\left( {5,1} \right) = \left( {5,1} \right)\]
Se cumple entonces ¡es verdadera la afirmación!
Ejercicio 4 – Espacios vectoriales
a) Halle la expresión analítica de \(W = gen\left\{ {\;1 + {x^2}\;,\;\;1 – x + {x^2}\;\;,\;\;1 + x + {x^2}} \right\}\)
b) Halle \(k \in \mathbb{R}\), si existen, para que \(p\left( x \right) = 2{x^2} + x + k\) pertenezca a \(W\).
Resolución del ejercicio 4
Ítem a
Los vectores de \(W\) son vectores de \({P_2}\) de la forma \({a_0} + {a_1}x + {a_2}{x^2}\) que son generados por \(\left\{ {\;1 + {x^2}\;,\;\;1 – x + {x^2}\;\;,\;\;1 + x + {x^2}} \right\}\). Tenemos que hallar qué relación existe entre \({a_0}\), \({a_1}\) y \({a_2}\) para que un vector pertenezca a \(W\).
Para eso podemos escribir a un vector genérico de \({P_2}\) y expresarlo cómo combinación lineal de los vectores de \(W\):
\[{a_0} + {a_1}x + {a_2}{x^2} = \alpha \left( {1 + {x^2}} \right) + \beta \left( {1 – x + {x^2}} \right) + \gamma \left( {1 + x + {x^2}} \right)\;\;\;\;\alpha ,\beta ,\gamma \in \mathbb{R}\]
\[{a_0} + {a_1}x + {a_2}{x^2} = \left( {\alpha + \beta + \gamma } \right){x^2} + \left( { – \beta + \gamma } \right)x + \left( {\alpha + \beta + \gamma } \right)\]
\[ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{a_0} = \alpha + \beta + \gamma }\\{{a_1} = – \beta + \gamma }\\{{a_2} = \alpha + \beta + \gamma }\end{array}} \right. \Rightarrow \;\;\left\{ {\begin{array}{*{20}{c}}{{a_0} = {a_2}}\\{{a_1} \in R}\end{array}} \right.\]
De acá se deduce que \({a_0}\) es igual a \({a_2}\), y que \({a_1}\) es libre.
Entonces:
\[W = \left\{ {{a_0} + {a_1}x + {a_2}{x^2} \in {P_2}\;|\;\;{a_0} = {a_2}} \right\}\]
Con esto ya está resuelto el ítem a.
Pero vamos a profundizar un poco a ver si ayuda a entender el tema mejor.
\(W\) quedó definido por una única restricción o ecuación: \({a_0} = {a_2}\).
Cómo \(W\) es subespacico de \({P_2}\), entonces \(W\) debe tener dimensión 2.
Recordemos la relación que hay entre el número de restricciones que definen a un subespacio y su dimensión:
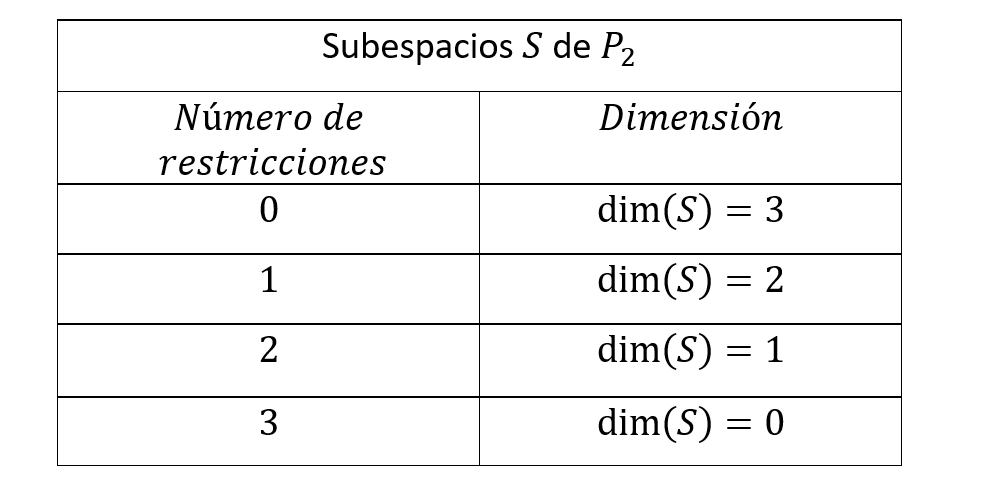
Intentemos hallar la dimensión de \(W\) respondiendo: ¿Es \(\left\{ {\;1 + {x^2}\;,\;\;1 – x + {x^2}\;\;,\;\;1 + x + {x^2}} \right\}\) un conjunto LI o LD?
Para ver si son LI o LD igualemos una combinación lineal de ellos al vector nulo y veamos si hay solución única (la trivial) o no.
\[0 + 0.x + 0.{x^2} = \alpha \left( {1 + {x^2}} \right) + \beta \left( {1 – x + {x^2}} \right) + \gamma \left( {1 + x + {x^2}} \right)\;\;\;\;\alpha ,\beta ,\gamma \in \mathbb{R}\]
\[0 + 0x + 0.{x^2} = \left( {\alpha + \beta + \gamma } \right){x^2} + \left( { – \beta + \gamma } \right)x + \left( {\alpha + \beta + \gamma } \right)\]
\[ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{\alpha + \beta + \gamma = 0}\\{ – \beta + \gamma = 0}\\{\alpha + \beta + \gamma = 0}\end{array}} \right. \Rightarrow \;\;\left\{ {\begin{array}{*{20}{c}}{\alpha = – 2\gamma }\\{\beta = \gamma }\end{array}} \right.\]
Vemos que el sistema es SCI (sistema compatible indeterminado). Es decir que hay infinitas soluciones. Esas soluciones son tales que \(\alpha = – 2\gamma \) y \(\beta = \gamma \).
Por ejemplo, si \(\gamma = 1\), entonces \(\alpha = – 2\) y \(\beta = 1\):
\[ – 2.\left( {1 + {x^2}} \right) + 1.\left( {1 – x + {x^2}} \right) + 1.\left( {1 + x + {x^2}} \right)\]
\[ – 2 – 2{x^2} + 1 – x + {x^2} + 1 + x + {x^2}\]
\[0{x^2} + 0x + 0\]
Es decir que podemos despejar cualquiera de esos vectores que generan W en función de los otros dos. Por ejemplo:
\[1 + {x^2} = \frac{1}{2}.\left( {1 – x + {x^2}} \right) + \frac{1}{2}.\left( {1 + x + {x^2}} \right)\]
Entonces una base de \(W\) es:
\[{B_W} = \left\{ {1 – x + {x^2}\;\;,\;\;\;1 + x + {x^2}\;\;} \right\}\]
\[ \Rightarrow \dim \left( W \right) = 2\]
Esto es coherente con el hecho de que encontramos una única restricción que define a \(W\).
Ítem b
Si \(p\left( x \right) = 2{x^2} + x + k\) pertenece a \(W\), debe cumplir sus ecuaciones.
Es decir que debe ser \({a_0} = {a_2}\).
Entonces \(k = 2\).
Ejercicio 5 – Espacios vectoriales
Dados \(S = \left\{ {\left( {x,y,z} \right) \in {\mathbb{R}^3}\;|\;x – y + z = 0\; \wedge \;\;2x + z = 0} \right\}\) , \(W = gen\left\{ {\left( {1,0,1} \right),\left( {h, – 1,1} \right)} \right\}\)
Halle todos los valores de h reales para que:
a) \(S \oplus W = {\mathbb{R}^3}\)
b) Halle \({S^ \bot }\)
Resolución del ejercicio 5
Ítem a
Recordemos que la suma es directa si la intersección es el vector nulo.
Es decir:
\(S + W\) es directa \( \Leftrightarrow S \cap W = \left\{ {\left( {0,0,0} \right)} \right\}\)
Cómo \(S\) y \(W\) son subespacios de \({\mathbb{R}^3}\).
- \(S\) es una recta que pasa por el origen (pues está definido cómo intersección de dos planos en R3)
- \(W\) es un plano que pasa por el origen pues es un subespacio de \({\mathbb{R}^3}\) con dimensión 2.
Una recta y un plano que pasan por el origen en general se cortan justamente en \(\left( {0,0,0} \right)\). Excepto si la recta está incluida en el plano.
Entonces queremos que el vector director de la recta NO esté incluido en el plano.
\[\overrightarrow {{v_s}} = \left| {\begin{array}{*{20}{c}}1&{ – 1}&1\\2&0&1\end{array}} \right| = \left( { – 1,1,2} \right)\]
\[\overrightarrow {{n_\pi }} = \left| {\begin{array}{*{20}{c}}1&0&1\\h&{ – 1}&1\end{array}} \right| = \left( {1, – 1 + h, – 1} \right)\]
Si la recta estuviera incluida en el plano el vector director de la recta sería perpendicular al normal del plano.
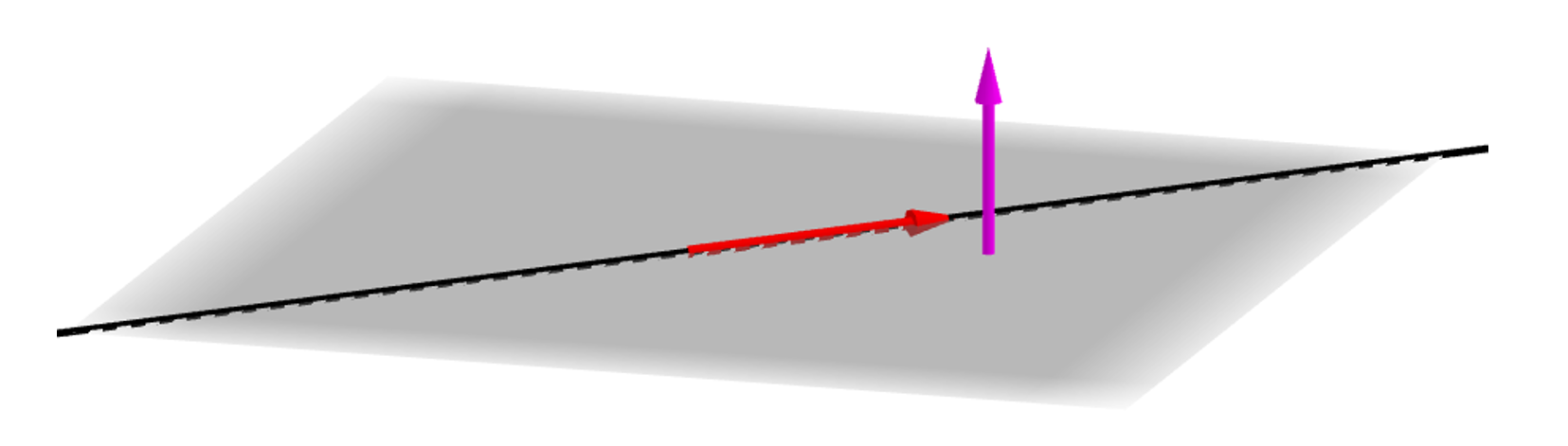
\[\left( { – 1,1,2} \right)\left( {1, – 1 + h, – 1} \right) = 0\]
\[ – 1 – 1 + h – 2 = 0\]
\[h = 4\]
Si \(h = 4\) la recta está incluida en el plano. Entonces para que NO esté incluida:
\[h \ne 4\]
Si \(h \ne 4\), entonces \(S \oplus W\).
Ítem b
\({S^ \bot }\) es el conjunto de vectores que son ortogonales a los de \(S\).
Pero cómo S es una recta… entonces \({S^ \bot }\) será el plano perpendicular.
\[\overrightarrow {{v_s}} = \left( { – 1,1,2} \right)\]
\[\vec n = \left( { – 1,1,2} \right)\]
\[{S^ \bot }:\pi : – x + y + 2z = 0\]

