Recta y plano: intersecciones y ángulos

Intersección entre recta y plano

¿Qué casos pueden presentarse en la intersección entre una recta y un plano?

Caso 1

Una recta puede ser concurrente con un plano:

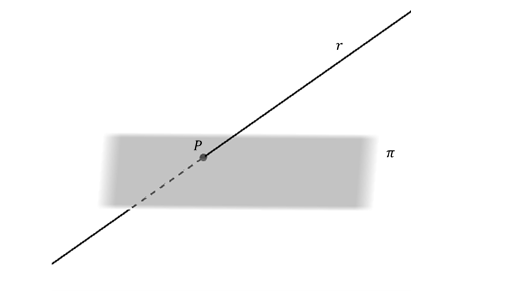
\[r \cap \pi = \left\{ P \right\}\]

Caso 2

Una recta puede ser paralela a un plano:

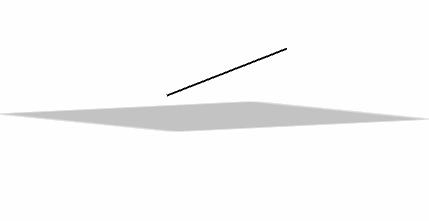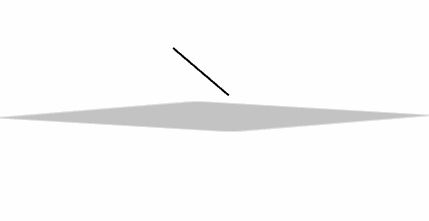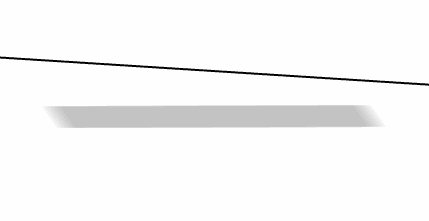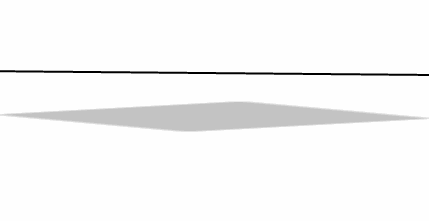
\[r\parallel \pi \]

\[r \cap \pi = \emptyset \]

Caso 3

Una recta puede estar incluida en un plano:

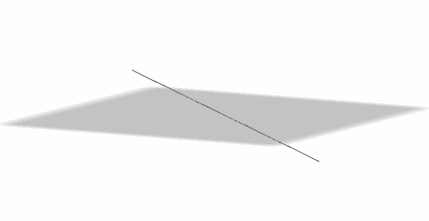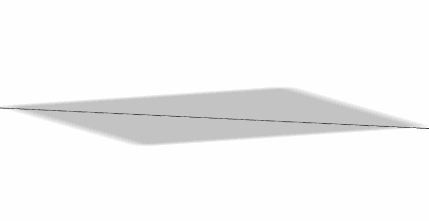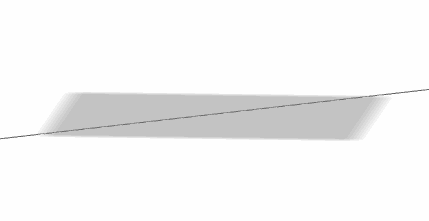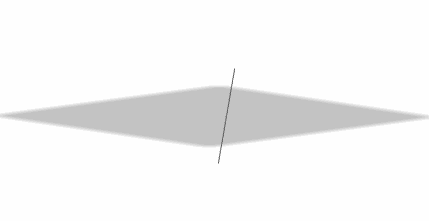
\[r \subset \pi \]

\[r \cap \pi = r\]

Ejemplos

Dados:

\[\pi :\;\;2x – 3y + z + 1 = 0\]

\[{r_1}:\left( {x,y,z} \right) = \left( {0,1,3} \right) + \alpha \left( {1,0,1} \right)\]

¿Cómo se busca la intersección entre la recta y el plano?

Escribimos las ecuaciones paramétricas de la recta y las reemplazamos en la ecuación del plano:

\[\left\{ {\begin{array}{*{20}{c}}{x = \alpha }\\{y = 1}\\{z = 3 + \alpha }\end{array}} \right.\]

\[2\alpha – 3.1 + \left( {3 + \alpha } \right) + 1 = 0\;\; \Rightarrow \;\alpha = – \frac{1}{3}\]

Reemplazando el valor del parámetro \(\alpha \) en las ecuaciones de la recta, obtenemos el punto de intersección:

\[{r_1} \cap \pi = \left\{ {\;\left( { – \frac{1}{3},1,\frac{8}{3}} \right)\;} \right\}\;\;\]

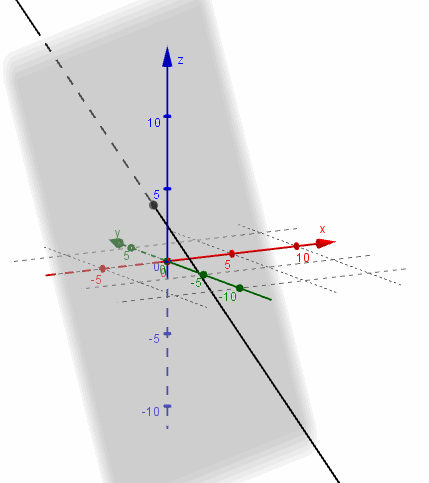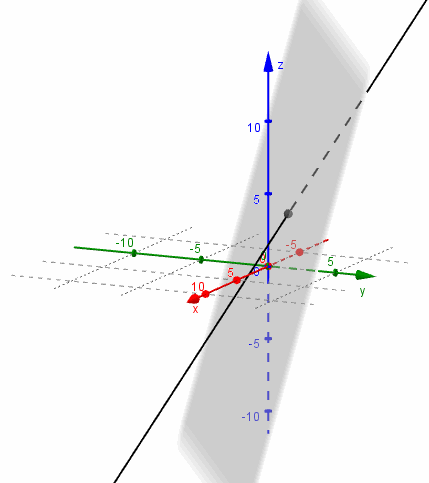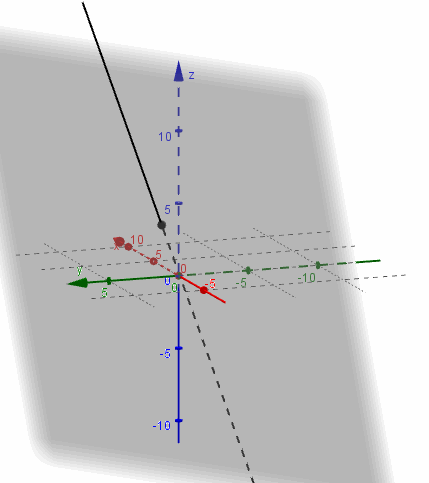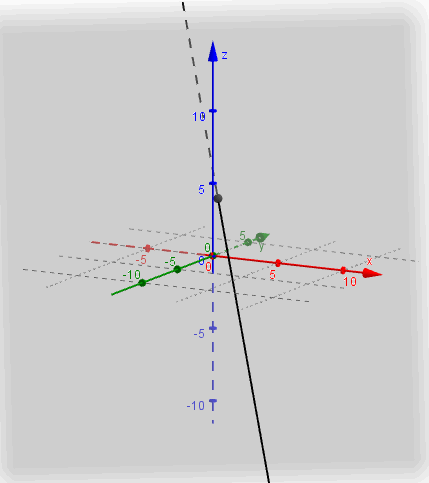
Busquemos ahora la intersección del mismo plano \(\pi \) con la recta

\[{r_2}:\;\left( {x,y,z} \right) = \left( {0,0, – 1} \right) + \lambda \left( {3,2,0} \right)\]

Escribimos las ecuaciones paramétricas:

\[\left\{ {\begin{array}{*{20}{c}}{x = 3\lambda }\\{y = 2\lambda }\\{z = – 1}\end{array}} \right.\]

Reemplazamos en la ecuación del plano

\[2\left( {3\lambda } \right) – 3\left( {2\lambda } \right) – 1 + 1 = 0\; \Rightarrow \;\;0 = 0\;\;\forall \lambda \]

Queda una expresión que es verdadera para todo \(\lambda \). Esto significa que todo punto de la recta verifica la ecuación del plano. En este caso podemos afirmar que la recta está incluida en el plano, por lo tanto: \({r_2} \cap \pi = {r_2}\;.\)

Considerando el mismo plano \(\pi \), hallemos la intersección con la recta

\[{r_3}:\left( {x,y,z} \right) = \left( {5,0,0} \right) + t\left( {0,1,3} \right)\]

Reiterando el procedimiento, resulta:

\[\left\{ {\begin{array}{*{20}{c}}{x = 5}\\{y = t}\\{z = 3t}\end{array}} \right.\]

\[10 – 3t + 3t + 1 = 0\; \Rightarrow \;11 = 0\;\;\;\;absurdo\]

Este absurdo nos indica que la recta y el plano no tienen ningún punto en común, o sea que la recta es paralela al plano y por lo tanto: \(r \cap \pi = \emptyset \)

En resumen:

Paralelismo entre recta y plano

¿Existe una manera de anticipar si una recta es paralela a un plano sin buscar la intersección?

Una vez más, los vectores resultarán una herramienta potente para la geometría de rectas y planos. Observemos la siguiente figura:

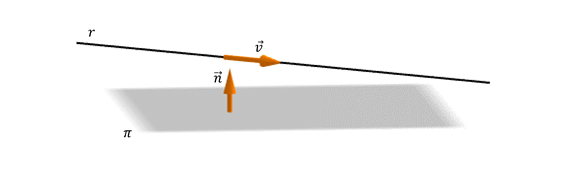
¿Cómo deben ser el vector normal del plano y el vector director de la recta para que \(r\parallel \pi \;\;\)?

¿Qué ocurre si la recta está incluida en el plano?

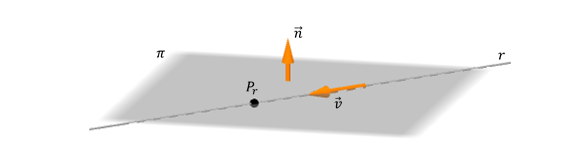
En este caso también se verifica que el vector director de la recta es perpendicular al normal del plano. Pero a diferencia del caso anterior, todos los puntos de la recta están en el plano. Esto nos permite afirmar que:

Ejemplo

Dados el plano \(\pi :\;x + y – z – 3 = 0\) y la recta \(r:\left( {x,y,z} \right) = \left( {1,0,0} \right) + t\left( {0,2,2} \right)\), comprobar que la recta es paralela al plano. ¿Está incluida en el plano?

Si la recta es paralela al plano entonces su vector director \(\vec v\) debe ser perpendicular al vector normal del plano \(\vec n\). Luego \(\vec n.\vec v\) debe ser cero:

\[\left( {1,1, – 1} \right)\left( {0,2,2} \right) = 2 – 2 = 0\]

Para saber si la recta está incluida en el plano veamos si el punto \(\left( {1,0,0} \right)\) satisface la ecuación del plano \(\pi \):

\[1\; + 0 – 0 – 3 = 0 \Rightarrow \; – 2 = 0\;\;Abs!\]

Como el punto no satisface la ecuación podemos concluir que \(r\) no está incluida en \(\pi \).

Ejercicio para el lector 3

Sea \(\;\pi \) el plano paralelo al eje \(\;y\) que pasa por \(\left( {1,1,1} \right)\) y \(\left( {1,2,3} \right)\), y

\[r:\;\left\{ {\begin{array}{*{20}{c}}{x – y = 0}\\{x + kz = 2}\end{array}} \right.\]

Hallar, si es posible, el valor de \(k\) para que la recta \(r\) sea paralela a \(\pi \).

Si existe \(k\), analizar si \(r \subset \pi \).

Respuesta: \(k=0\) y la recta no pertenece al plano.

Perpendicularidad entre recta y plano

Así como encontramos una condición vectorial para el paralelismo entre una recta y un plano, nos preguntamos si existirá una condición para la perpendicularidad. Observemos la siguiente figura:

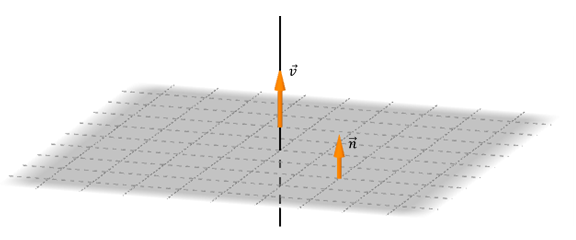
¿Cómo deben ser el vector normal del plano y el vector director de la recta para que \(r \bot \pi \;\;\)?

Ejemplo

Dado el plano \(\pi :\;\;x\;–\;3y\; + \;z\; + \;1\; = \;0\) , hallar la ecuación de la recta perpendicular a \(\pi \) que pasa por \(A\left( {1,0,3} \right)\).

Como la recta es perpendicular al plano \(\pi \) entonces su vector director es paralelo al vector normal del plano. Podemos tomar:

\[\vec v = \left( {1, – 3,1} \right)\]

Ya tenemos el vector director y un punto de paso, luego la ecuación vectorial es:

\[r:\left( {x,y,z} \right) = \left( {1,0,3} \right) + \lambda \;\left( {1, – 3,1} \right)\;\;,\;\;\;\lambda \in \mathbb{R}\]

Ejercicio para el lector 4

Dado el haz de planos \(x\; + \;y\;–\;z\; + \;2\; + \;k\;\left( {x\;–\;y\; + \;z} \right)\; = \;0\) , analizar si existe algún plano del haz que sea perpendicular a la recta \(r:\;\left\{ {\begin{array}{*{20}{c}}{x – 1 = 0}\\{y – z = 0}\end{array}} \right.\) .

Ángulo entre recta y plano

Consideremos el siguiente esquema:

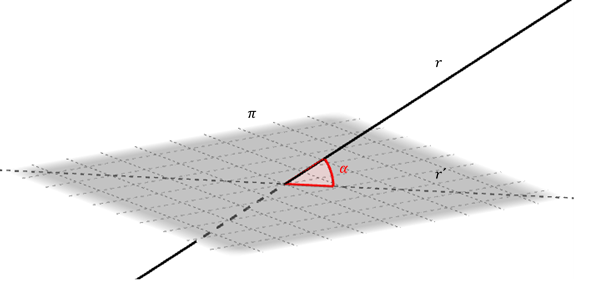
Sea \(r\) una recta no paralela ni perpendicular a un plano \(\pi \). Sea la proyección ortogonal de \(r\) sobre \(\;\pi \). Se define como ángulo entre \(r\) y \(\;\pi \) al ángulo agudo que forman \(r\) y \(r’\).

¿Cómo podemos hallar dicho ángulo? Veamos la siguiente figura:

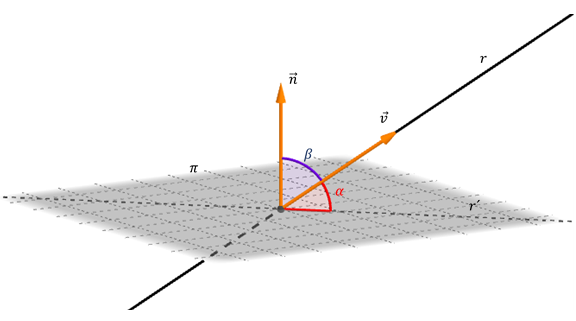
Podemos calcular el ángulo \(\beta \) entre \(\vec v\;\) y \(\;\vec n\) :

\[\cos \left( \beta \right) = \frac{{\vec v.\vec n}}{{\lVert\vec v\rVert\;\lVert\vec n\rVert}}\]

Como habíamos visto previamente, de acuerdo con las direcciones de \(\vec v\;\) y \(\vec n\) el ángulo \(\beta \) podría ser mayor de 90º. Agregamos módulo para obtener un ángulo agudo:

\[\cos \;\left( \beta \right) = \frac{{\left| {\overrightarrow {\;v} .\overrightarrow {n\;} } \right|}}{{\lVert\vec v\rVert\;\lVert\vec n\rVert}}\;\]

Como \(\alpha \) y \(\beta \) son complementarios se cumple que \(sen\left( \alpha \right) = \cos \left( \beta \right)\), entonces:

\[sen\left( \alpha \right) = \frac{{\left| {\;\vec v.\vec n\;} \right|}}{{\lVert\vec v\rVert\;\lVert\vec n\rVert}}\;\;\;\]

Por lo tanto:

Casos particulares:

• Si \({\rm{\;}}\alpha = 0\) , entonces la recta es paralela al plano (\(\overrightarrow {\;v} .\overrightarrow {n\;} = 0\)).
• Si \(\alpha = \frac{\pi }{2}\) , entonces la recta es perpendicular al plano (\(\overrightarrow {\;v} = k\;\overrightarrow {n\;} \)).

Ejemplo

Hallar el ángulo entre el plano \(\pi :\;x + z – 8 = 0\) y el eje \(x\).

Conocemos el vector normal de \(\pi \) y el vector director de la recta. Luego aplicamos directamente la fórmula:

\[\alpha = {\rm{arcsen}}\left( {\frac{{\left| {\overrightarrow {\;v} .\overrightarrow {n\;} } \right|}}{{\lVert\vec v\rVert\;\lVert\vec n\rVert}}} \right) = {\rm{arcsen}}\left( {\frac{{\left| {\left( {1,0,0} \right).\left( {1,0,1} \right)} \right|}}{{\sqrt 2 }}} \right) = {\rm{arcsen}}\left( {\frac{1}{{\sqrt 2 }}} \right) = \frac{\pi }{4}\]

Intersección de rectas en \({\mathbb{R}^3}\)

Sabemos que dos rectas en \({\mathbb{R}^2}\) o bien se cortan en un único punto o bien son paralelas.

Pero en \({\mathbb{R}^3}\), además de estos dos casos, existen rectas que ni se cortan ni son paralelas: son las rectas alabeadas.

Tenemos entonces tres casos en \({\mathbb{R}^3}\):

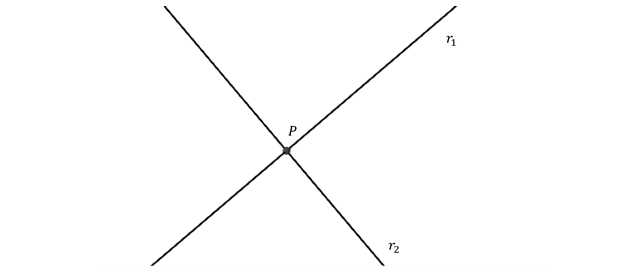
Caso 1: Rectas concurrentes o incidentes

\[{r_1} \cap {r_2} = \left\{ P \right\}\]

Caso 2: Rectas paralelas

\[{r_1}\parallel {r_2}\; \Leftrightarrow \;{\vec v_1} = k{\vec v_2}\]

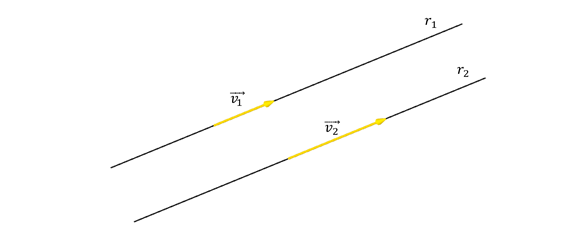
Las rectas paralelas podrían ser coincidentes. Para verificar si dos rectas paralelas son coincidentes basta con ver si un punto de una de ellas pertenece o no a la otra recta.

Caso 3: Rectas alabeadas

Existe otra posición posible para las rectas en \({\mathbb{R}^3}\). Consideremos el siguiente esquema en el que las rectas \({r_1}\), \({r_2}\) y \({r_3}\) contienen a las aristas de un cubo:

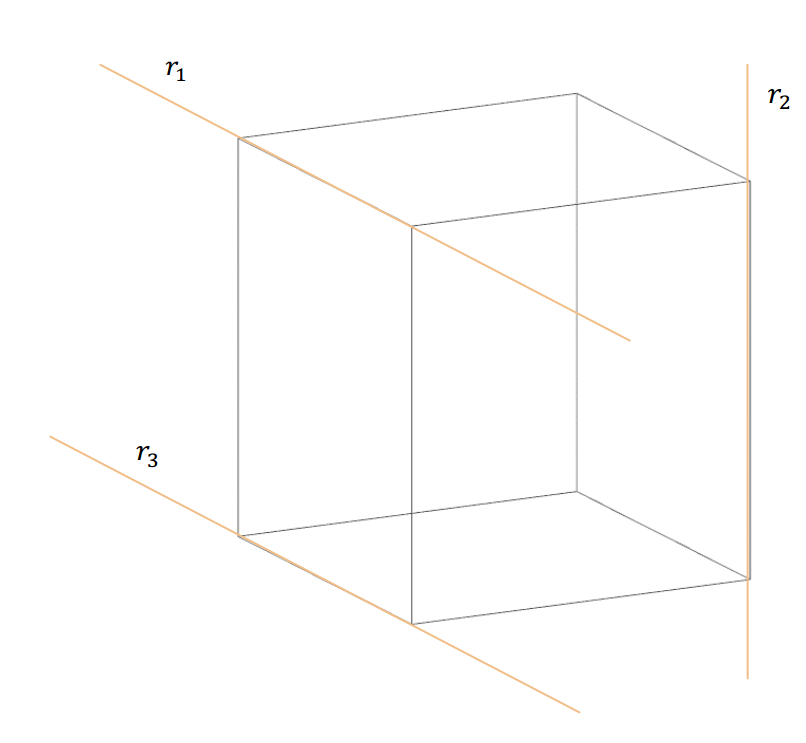
Las rectas \({r_1}\) y \({r_3}\) son paralelas. En cambio \({r_1}\) y \({r_2}\), que no son paralelas ni concurrentes, se denominan alabeadas.

Ejemplo

Hallar la intersección entre las rectas:

\[{r_1}:\left( {x,y,z} \right) = \left( { – 2,1,3} \right) + \alpha \left( {1,4,5} \right)\]

\[{r_2}:\left( {x,y,z} \right) = \left( {1,0, – 2} \right) + \beta \left( {0,3, – 1} \right)\]

Para buscar la intersección, escribimos las ecuaciones paramétricas de las rectas y luego igualamos:

\[{r_1}:\left\{ {\begin{array}{*{20}{c}}{x = – 2 + \alpha }\\{y = 1 + 4\alpha }\\{z = 3 + 5\alpha }\end{array}} \right.\;\;\;\;\;\;\;,\;\;\;\;\;\;\;{r_2}:\left\{ {\begin{array}{*{20}{c}}{x = 1}\\{y = 3\beta }\\{z = – 2 – \beta }\end{array}} \right.\]

\[ \Rightarrow \;\left\{ {\begin{array}{*{20}{c}}{ – 2 + \alpha = 1}\\{1 + 4\alpha = 3\beta }\\{3 + 5\alpha = – 2 – \beta }\end{array}} \right.\]

Nos queda un sistema de tres ecuaciones y dos incógnitas.

De la primera ecuación se obtiene: \(\alpha = 3\)

Reemplazando \(\alpha = 3\) en la segunda ecuación, resulta: \(\beta = \frac{{13}}{3}\)

Pero si sustituimos ambos valores en la tercera ecuación:

\[3 + 5.3 = – 2 – \frac{{13}}{3}\]

\[18 = – \frac{{19}}{3}\]

Como esto es falso, el sistema es incompatible. Habíamos descartado paralelismo, por lo tanto podemos afirmar que las rectas son alabeadas.

Observación: Los sistemas que tienen más ecuaciones que incógnitas se denominan sobredeterminados y en general son incompatibles.

Ejemplo

Hallar la intersección entre las rectas:

\[{r_1}:\left( {x,y,z} \right) = \lambda \left( {1,0,1} \right)\]

\[{r_2}:\left( {x,y,z} \right) = \beta \left( { – 1,1,0} \right) + \left( {0,1,1} \right)\]

Observemos que los vectores directores de las rectas no son paralelos, luego las rectas no pueden ser paralelas. Podrían intersecarse o ser alabeadas.

Escribimos las ecuaciones paramétricas de las rectas e igualamos:

\[{r_1}:\;\left\{ {\begin{array}{*{20}{c}}{x = \lambda }\\{y = 0}\\{z = \lambda }\end{array}} \right.\;\;\;\;\;\;,\;\;\;\;\;{r_2}:\left\{ {\begin{array}{*{20}{c}}{x = – \beta }\\{y = \beta + 1}\\{z = 1}\end{array}} \right.\]

\[\left\{ {\begin{array}{*{20}{c}}{\lambda = – \beta }\\{0 = \beta + 1}\\{\lambda = 1}\end{array}} \right.\;\;\; \Rightarrow \;\lambda = 1\; \wedge \;\beta = – 1\]

Como el sistema tiene solución, podemos afirmar que las rectas se intersecan, o sea son concurrentes. Para averiguar en qué punto se cortan, podemos reemplazar \(\lambda = 1\) en las ecuaciones paramétricas de \({r_1}\) o \(\beta = – 1\) en las ecuaciones paramétricas de \({r_2}\). Así obtenemos el punto de intersección \(\;P\left( {1,0,1} \right).\)

Observación: En este ejemplo, las rectas se cortan en el punto \(P\left( {1,0,1} \right)\). En \({r_1}\), el punto \(P\) se corresponde con \(\lambda = 1\). En cambio en \({r_2}\), \(P\) se corresponde con \(\beta = – 1\). Por lo tanto, cuando buscamos la intersección entre dos rectas debemos utilizar letras diferentes para indicar los respectivos parámetros. Noten que si hubiéramos utilizado el parámetro \(\lambda \) para las dos rectas, habríamos obtenido un absurdo: \(\lambda = 1\;\;y\;\;\lambda = \; – 1\) y esto nos habría inducido a error.

Plano que contiene a dos rectas

Habíamos visto que dos rectas en \({\mathbb{R}^3}\) pueden ser concurrentes, paralelas o alabeadas. Veamos en qué casos es posible encontrar un plano que las contenga:

Caso 1: Rectas concurrentes

Veamos el siguiente gráfico que muestra dos rectas concurrentes:

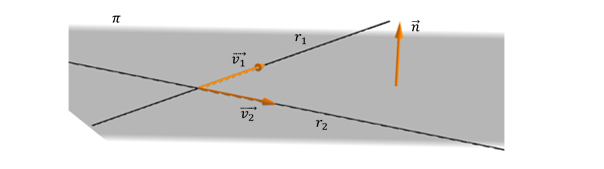
Dadas dos rectas concurrentes \({r_1}\) y \({r_2}\), ¿cómo podemos encontrar el vector normal del plano?

\[{\vec v_1} \times {\vec v_2} = \vec n\]

Para completar la ecuación del plano, tomamos un punto P de cualquiera de las dos rectas.

Ejemplo

\[{r_1}:\;\left( {x,y,z} \right) = \left( {1,1,1} \right) + t\left( {0,1,2} \right)\]

\({r_2}:\;\;\)Recta que pasa por\(\;\;A\left( {0,1, – 1} \right)\;\;y\;\;\;B\left( {1,2,{z_0}} \right)\)

Hallar \({z_0}\) para que las rectas sean concurrentes y encontrar el plano que las contiene.

Resolución

Construyamos una ecuación vectorial de la recta \({r_2}\):

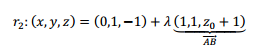
Escribimos las ecuaciones paramétricas de cada recta:

\[{r_1}:\left\{ {\begin{array}{*{20}{c}}{x = 1}\\{y = 1 + t}\\{z = 1 + 2t}\end{array}} \right.\;\;\;\;,\;\;\;\;{r_2}:\left\{ {\begin{array}{*{20}{c}}{x = \lambda }\\{y = 1 + \lambda }\\{z = – 1 + \left( {1 + {z_0}} \right)\lambda }\end{array}} \right.\]

Igualamos:

\[\left\{ {\begin{array}{*{20}{c}}{1 = \lambda }\\{1 + t = 1 + \lambda }\\{1 + 2t = – 1 + \lambda \left( {{z_0} + 1} \right)}\end{array}} \right.\]

De las dos primeras ecuaciones, se obtiene \(t = \lambda = 1\)

Reemplazamos en la tercera ecuación y despejamos \({z_0}\):

\[3 = – 1 + {z_0} + 1\; \Rightarrow {z_0} = 3\]

Para \({z_0} = 3\) las rectas se cortan.

¿Cuál es el punto de intersección? Reemplazamos por \(t = 1\) en la ecuación de la primera recta:

\[{r_1} \cap {r_2} = \left\{ {\left( {1,2,3} \right)} \right\}\]

Para obtener la ecuación del plano que contiene a las rectas, buscamos el vector normal:

\[\vec n = \overrightarrow {{v_1}} \times \overrightarrow {{v_2}} = \left| {\begin{array}{*{20}{c}}i&j&k\\0&1&2\\1&1&4\end{array}} \right| = \left( {2,2, – 1} \right)\]

\[\pi :\;\;2x + 2y – z + d = 0\]

Para averiguar \(d\) reemplazamos un punto que pertenezca al plano. Puede ser cualquier punto de las rectas, por ejemplo \(\left( {1,1,1} \right)\):

\[2.1 + 2.1 – 1.1 + d = 0 \Rightarrow d = – 3\]

\[\pi :\;2x + 2y – z – 3 = 0\]

Caso 2: Rectas paralelas

Veamos el siguiente gráfico que muestra dos rectas paralelas y el plano que las contiene:

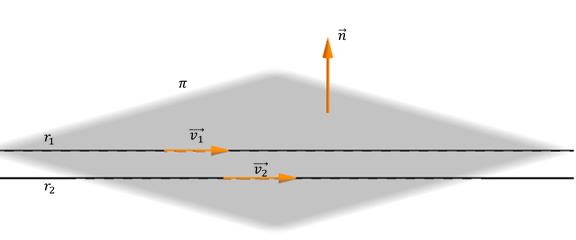
Dadas dos rectas paralelas, existe un plano que las contiene pero no podemos hallar el vector normal como en el caso de las rectas concurrentes. ¿Por qué?

Ejemplo

\[{r_1}:\left( {x,y,z} \right) = \left( {1,2,3} \right) + \lambda \left( { – 1,1,4} \right)\]

\[{r_2}:\left( {x,y,z} \right) = \left( {1,0,0} \right) + t\left( {3, – 3, – 12} \right)\]

Claramente son paralelas pues sus vectores directores son paralelos:

\(\left( {3, – 3, – 12} \right) = – 3.\left( { – 1,1,4} \right)\).

El lector puede comprobar que \(\left( { – 1,1,4} \right) \times \left( {3, – 3, – 12} \right) = \vec 0\) , entonces el vector normal del plano no puede hallarse con este producto vectorial.

Para hallar el vector normal, consideramos uno de los vectores directores y un vector \(\overrightarrow {{P_1}{P_2}} \) determinado por un punto de cada recta, como muestra la figura:

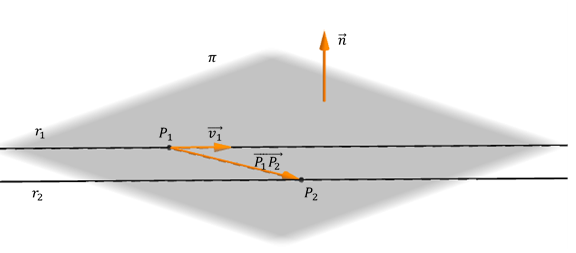
El producto vectorial de ambos da un vector normal al plano:

\[\vec n = \vec v \times \overrightarrow {{P_1}{P_2}} \]

Para completar la ecuación del plano, consideramos un punto de cualquiera de las rectas. Así obtenemos la ecuación del plano que contiene a las rectas dadas:

\[\pi :\;\;5x – 3y + 2z – 5 = 0\]

Caso 3: Rectas alabeadas

Dos rectas alabeadas no pueden estar contenidas en un mismo plano.

Ejemplo

Hallar, si es posible, el plano que contiene a las rectas:

\[{r_1}:\;\left( {x,y,z} \right) = \lambda \left( {1,0,0} \right)\]

\[{r_2}:\left( {x,y,z} \right) = \left( {0,1,0} \right) + t\left( {0,0,1} \right)\]

Dejamos a cargo del lector la verificación de que son alabeadas. Busquemos un vector perpendicular a ambas rectas:

\[\vec n = \left( {1,0,0} \right) \times \left( {0,0,1} \right) = \left( {0, – 1,0} \right)\]

Considerando el punto \(\left( {0,0,0} \right)\) perteneciente a \({r_1}\), obtenemos el siguiente plano:

\[\pi :\;\;y\; = \;0\]

Sin embargo, este plano no contiene a \({r_2}\), pues el punto \(\left( {0,1,0} \right)\) no verifica la ecuación de \(\pi \).

Sugerimos al lector hacer una gráfico de las rectas y el plano obtenido, para visualizar la situación.

No es posible hallar un plano que contenga a dos rectas alabeadas. Las rectas alabeadas no son coplanares.

Ángulo entre dos rectas

Definición: El ángulo entre dos rectas de \({\mathbb{R}^3}\) es el ángulo entre sus vectores directores.

Sean las rectas \({r_1}\) y \({r_2}\) con vectores directores \(\overrightarrow {{v_1}} \) y \(\overrightarrow {{v_2}} \). . Entonces:

\[\cos \left( \alpha \right) = \frac{{\overrightarrow {{v_1}} .\overrightarrow {{v_2}} }}{{\lVert\overrightarrow {{v_1}}\rVert \;\lVert\overrightarrow {{v_2}}\rVert \ }}\]

Usamos la misma convención que para ángulo entre planos y para ángulo entre recta y plano, y aplicamos módulo:

\[\cos \left( \alpha \right) = \frac{{\left| {\overrightarrow {{v_1}} .\overrightarrow {{v_2}} } \right|}}{{\lVert\overrightarrow {{v_1}}\rVert \ \;\lVert\overrightarrow {{v_2}}\rVert \ }}\]

Por lo tanto:

Casos particulares:

Si \({\rm{\;}}\alpha = 0\) , entonces las rectas son paralelas (\(\overrightarrow {\;{v_1}} = k\;\overrightarrow {{v_2}\;} \)).

Si \(\alpha = \frac{\pi }{2}\) , entonces las rectas son perpendiculares (\(\overrightarrow {\;{v_1}} .\overrightarrow {{v_2}} = 0\)).

Observación: La definición de ángulo que hemos adoptado no toma en cuenta si las rectas se cortan o no.

Ejemplo

Sean,

\[{r_1}:\left( {x,y,z} \right) = \lambda \left( {1,0,0} \right)\;\;\;\lambda \in \mathbb{R}\]

\[{r_2}:\left( {x,y,z} \right) = \left( {0,1,0} \right) + t\left( {0,0,1} \right)\;\;t \in \mathbb{R}\;\]

Vimos en un ejemplo anterior que estas rectas son alabeadas. ¿Cuál es el ángulo entre ellas?

Como \(\;\;\overrightarrow {\;{v_1}} .\overrightarrow {{v_2}} = 0\) , las rectas son perpendiculares, o sea que \(\alpha = \frac{\pi }{{2\;\;}}\)