Proyecciones ortogonales
Proyección de un punto sobre un plano
Dados un plano \(\pi \) y un punto A no perteneciente a dicho plano, la proyección ortogonal de A sobre \(\pi \) es el punto \(A’ \in \pi \) tal que \(\overrightarrow {AA’} \) es un vector perpendicular a \(\pi \).
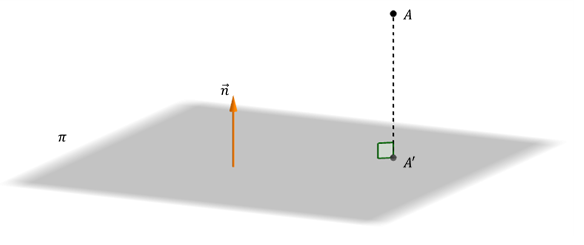
\[A’ = pro{y_\pi }\left( A \right)\;\;\;si\;y\;só lo\;si\;\;\;\left\{ {\begin{array}{*{20}{c}}{\;A’ \in \pi }\\{\;\;\overrightarrow {AA’} \bot \pi }\end{array}} \right.\]
Ejemplo
Dados un plano \(\pi \) y un punto \(A\), obtener la proyección ortogonal del punto sobre el plano:
\[\pi :\;\;2x – y + 3z + 1 = 0\]
\[A\left( {4,1, – 3} \right)\]
Para obtener buscamos la recta perpendicular a \(\pi \) que pasa por \(A\). El vector normal del plano es paralelo a esta recta, por lo tanto podemos tomarlo como vector director:
\[r:\left( {x,y,z} \right) = \left( {4,1, – 3} \right) + \lambda \left( {2, – 1,3} \right)\]
Ahora buscamos la intersección de la recta con el plano, reemplazando las ecuaciones paramétricas de la recta en la ecuación del plano:
\[\left\{ {\begin{array}{*{20}{c}}{x = 4 + 2\lambda }\\{y = 1 – \lambda }\\{z = – 3 + 3\lambda }\end{array}} \right.\]
\[2\left( {4 + 2\lambda } \right) – \left( {1 – \lambda } \right) + 3.\left( { – 3 + 3\lambda } \right) + 1 = 0\]
\[8 + 4\lambda – 1 + \lambda – 9 + 9\lambda + 1 = 0\]
\[14\lambda – 1 = 0 \Rightarrow \lambda = \frac{1}{{14}}\]
Reemplazamos en la ecuación de la recta para obtener as coordenadas del punto \(A’\;\):
\[\left( {x,y,z} \right) = \left( {4,1, – 3} \right) + \frac{1}{{14}}\left( {2, – 1,3} \right) = \left( {4,1, – 3} \right) + \left( {\frac{1}{7}, – \frac{1}{{14}},\frac{3}{{14}}} \right) = \left( {\frac{{29}}{7},\frac{{13}}{{14}}, – \frac{{39}}{{14}}} \right)\;\;\]
El lector puede verificar que \(A’\left( {\frac{{29}}{7},\frac{{13}}{{14}}, – \frac{{39}}{{14}}} \right) \in \pi \;\;\;\;y\;\;\;\;\overrightarrow {AA’} \bot \pi \;.\).
Si \(A \in \pi \;,\) ¿cuál es la proyección de \(A\) sobre\(\;\pi \)?
Proyección de una recta sobre un plano
Dados una recta \(r\) y un plano \(\pi \), nos interesa obtener la proyección ortogonal de la recta sobre el plano.
En general, la proyección de una recta sobre un plano es otra recta \(r’\):
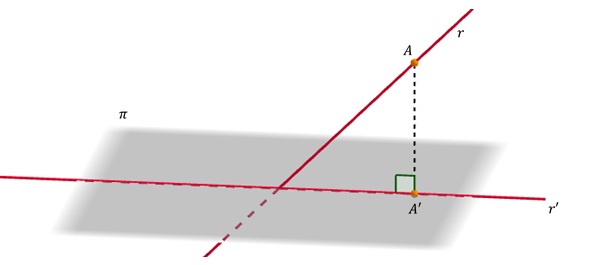
\[pro{y_\pi }\left( r \right) = r’\]
Para hallar podemos proyectar dos puntos de la recta sobre el plano. Si llamamos A y B a dichos puntos, resulta
\[pro{y_\pi }\left( A \right) = A’\;\;\;,\;\;\;\;pro{y_\pi }\left( B \right) = B’\;\;\;\;\]
La recta \(r’\) que buscamos es la recta determinada por \(A’\) y \(B’\).
Pero teniendo en cuenta que el punto de intersección entre la recta y el plano pertenece a \(r’\), es suficiente proyectar un solo punto de \(r\;\) para que \(r’\) quede definida.
También existe un caso especial: si la recta es perpendicular al plano, su proyección es un punto.
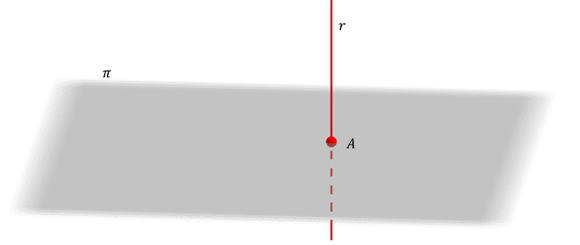
\[r \bot \pi \Rightarrow pro{y_\pi }\left( r \right) = A = r \cap \pi \]
Ejemplo
Dado \(\pi : x + y + z – 3 = 0\)
a) Hallar la proyección de la recta \(r:\left( {x,y,z} \right) = \lambda \left( {0,2,1} \right)\) sobre \(\pi \)
b) Dada la recta\(\;s:\left( {x,y,z} \right) = \left( {1,0,0} \right) + t.\left( { – 2,b,c} \right)\), hallar los valores de \(b\) y \(c\) para que la proyección de \(s\) sobre \(\pi \) sea un punto. ¿Cuál es dicho punto?
Resolución
Parte A
Para hallar la recta \(r’ = pro{y_\pi }\left( r \right)\) buscamos dos puntos que pertenezcan a \(r’\).
Uno de los puntos puede ser el de intersección:
\[2\lambda + \lambda – 3 = 0 \Rightarrow \;\lambda = 1 \Rightarrow \left( {x,y,z} \right) = \left( {0,2,1} \right)\]
Tomemos el punto \(\left( {0,0,0} \right) \in r\). Para proyectarlo sobre el plano buscamos la recta perpendicular al plano que pasa por \(\left( {0,0,0} \right)\):
\[\left( {x,y,z} \right) = \left( {0,0,0} \right) + \alpha \left( {1,1,1} \right)\]
\[\left( {x,y,z} \right) = \alpha \left( {1,1,1} \right)\]
Reemplazando en la ecuación del plano:
\[\alpha + \alpha + \alpha – 3 = 0 \Rightarrow \alpha = 1\]
Entonces la proyección del punto \(\left( {0,0,0} \right)\) sobre \(\pi \) da \(\left( {1,1,1} \right)\;\)
La recta \(r’\) queda definida por los puntos \(\left( {0,2,1} \right)\) y \(\left( {1,1,1} \right)\):
\[r’:\left( {x,y,z} \right) = \left( {0,2,1} \right) + \gamma \left( {1, – 1,0} \right)\]
Parte B
Para que la proyección de \(s\) sobre \(\pi \) sea un punto, el vector director de \(s\) debe ser paralelo al vector normal del plano. Debe existir un \(k \in \mathbb{R}\) tal que:
\[\left( {1,1,1} \right) = k\left( { – 2,b,c} \right)\]
De aquí deducimos que deben ser \(b = c = – 2\). La ecuación de la recta queda:
\[s:\;\left( {x,y,z} \right) = \left( {1,0,0} \right) + t\left( { – 2, – 2, – 2} \right)\]
Para hallar el punto reemplazamos las ecuaciones paramétricas de la recta en la ecuación del plano:
\[s:\;\left\{ {\begin{array}{*{20}{c}}{x = 1 – 2t}\\{y = – 2t}\\{z = – 2t}\end{array}} \right.\;\;\;\;t \in \mathbb{R}\;\;\;\;,\;\;\;\;\pi : x + y + z – 3 = 0\;\;\]
\[1 – 2t – 2t – 2t – 3 = 0 \Rightarrow – 2 – 6t = 0 \Rightarrow t = – \frac{1}{3}\]
El punto es:
\[P\left( {\frac{5}{3},\frac{2}{3},\frac{2}{3}} \right)\]
Por lo tanto:
\[pro{y_\pi }\left( s \right) = \;s \cap \pi = \;P\left( {\frac{5}{3},\frac{2}{3},\frac{2}{3}} \right)\]
Ejercicio para el lector 5
Sean:
\[\pi :\left( {x,y,z} \right) = \left( {0,1,0} \right) + \alpha \left( {1,1,1} \right) + \beta \left( {0,0,1} \right)\]
\[r:\left( {x,y,z} \right) = \left( {1,3,1} \right) + t\;\left( {k,2, – 1} \right)\]
Determinar el valor de \(k\) para que \(r\) sea paralela a \(\pi \). y obtener la proyección de \(r\) sobre \(\pi \).
Planos proyectantes de una recta
Los planos proyectantes de una recta son aquellos planos que incluyen a la recta y son perpendiculares a los planos coordenados.
Ejemplo
Hallar los planos proyectantes de la siguiente recta:
\[r:\;\left\{ {\begin{array}{*{20}{c}}{x – 2y + z + 7 = 0}\\{ – x + y + z – 1 = 0}\end{array}} \right.\]
Resolución
Teniendo en cuenta que la recta está definida como intersección de dos planos, una forma práctica de hallar los planos proyectantes es construir el haz de planos que pasan por dicha recta:
Construyamos el haz de planos que pasa por \(r\):
\[\mathcal{H}:\alpha \left( {x – 2y + z + 7} \right) + \beta \left( { – x + y + z – 1} \right) = 0\]
Ahora distribuimos y reordenamos:
![]()
El plano proyectante perpendicular al plano \(xy\) (o sea, paralelo al eje \(z\)) es un plano de la forma \(ax\; + \;by\; + \;d\; = \;0\). Por lo tanto:
\[\alpha + \beta = 0 \Rightarrow \alpha = – \;\beta \]
\[ \Rightarrow \;\;{\pi _1}:\;\; – 2x + 3y – 8 = 0\]
El plano proyectante perpendicular al plano \(xz\) (o sea, paralelo al eje y) es un plano de la forma \(ax\; + \;cz\; + \;d\; = \;0\). Por lo tanto:
\[ – 2\alpha + \beta = 0 \Rightarrow \beta = 2\alpha \]
\[ \Rightarrow \;{\pi _2}:\;\; – x + 3z + 5 = 0\]
¿Cuál es el plano proyectante perpendicular al plano \(yz\)?
Ejemplo
Hallar los planos proyectantes de la recta que pasa por los puntos \(A\left( {1,2,3} \right)\) y \(B\left( {3,1, – 1} \right)\).
Resolución
La ecuación vectorial de la recta \(AB\) es \(r:\;\;\left( {x,y,z} \right) = \left( {1,2,3} \right) + \;t\left( {2, – 1, – 4} \right)\)
Llamemos \({\pi _1}\) al plano proyectante que es perpendicular al plano \(xy\). ¿Qué condiciones debe cumplir \(\overrightarrow {{n_1}} \)?
Entonces: \(\left( {a,b,0} \right)\;.\left( {2, – 1, – 4} \right) = 0 \Rightarrow 2a – b = 0 \Rightarrow b = 2a\)
Con \(a = 1\;\;\;y\;\;b = 2\) , resulta:
Teniendo en cuenta que \(r \subset {\pi _1}\) , reemplazamos un punto de la recta (por ejemplo A) para obtener \(d\).
El plano buscado es: \({\pi _1}\;:\;\;x + 2y – 5 = 0\)
Dejamos a cargo del lector comprobar que los otros planos proyectantes son:
\({\pi _2}:\;\;2x + z – 5 = 0\) y \({\pi _3}:\; – 4y + z + 5 = 0\)
Ejemplo
Retomemos el ejemplo anterior, siendo \(r:\;\;\left( {x,y,z} \right) = \left( {1,2,3} \right) + \;t\left( {2, – 1, – 4} \right)\)
Cuando las componentes del vector director de una recta son distintas de cero, podemos expresarla a través de sus ecuaciones simétricas. En este caso:
\[r:\;\;\;\;\;\frac{{x – 1}}{2} = \frac{{y – 2}}{{ – 1}} = \frac{{z – 3}}{{ – 4}}\]
A partir de las ecuaciones simétricas se deducen tres igualdades, cada una de las cuales se corresponde con la ecuación de un plano proyectante de la recta:
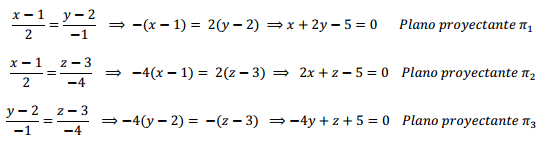
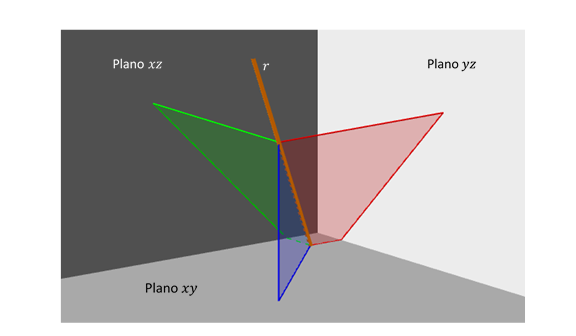
El siguiente gráfico muestra la recta y su plano proyectante \({\pi _1}:\)
Recta y un plano proyectante
En la figura puede observarse que el plano proyectante \({\pi _1}\) es el plano determinado por la recta\(\;r\) y su proyección \(r’\) sobre el plano coordenado \(xy\). Lo mismo puede afirmarse de los otros dos planos proyectantes.
Ejercicio para el lector 6
Hallar los planos proyectantes de cada una de las siguientes rectas:
\[r:\;\;\left( {x,y,z} \right)\; = \;\left( {1,2,3} \right)\; + \;t\left( {1, – 2,0} \right)\]
\[s:\;\;\;\left( {x,y,z} \right)\; = \;\left( {2,2,1} \right)\; + \;\lambda \left( {0,0,1} \right)\]
A partir de los resultados obtenidos, ¿podrían establecer qué condición debe cumplirse para que una recta tenga dos de sus planos proyectantes iguales?
¿Existe algún caso en que no esté definido alguno de los planos proyectantes de una recta?
Distancias
Distancia punto-recta en \({\mathbb{R}^3}\)
Dados un punto \(A\) y una recta \(r\) de vector director \(\vec v\), queremos hallar la distancia entre \(A\) y \(r\) (con \(A \notin r\)). Sea \(A’ \in r\) tal que \(\overrightarrow {AA’} \) es perpendicular a la recta.
\[d\left( {A,r} \right) = \lVert\overrightarrow {AA’} \rVert\]
Consideremos un punto \(P \in r\) y el vector \(\overrightarrow {PA} \), y construyamos el paralelogramo determinado por \(\vec v\) y \(\overrightarrow {PA} \), tal como lo muestra la figura:
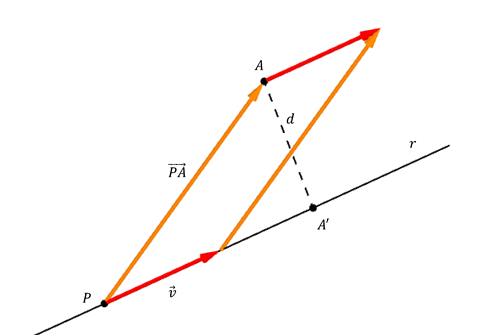
El segmento \(AA’\) es la altura del paralelogramo. Si llamamos S al área de dicho paralelogramo, resulta:
\[S = b.h = \lVert\vec v\rVert.d\;\;\;\;\;\;\;\;\left[ 1 \right]\]
Recordemos que el área del paralelogramo es igual al módulo del producto vectorial:
\[S = \lVert\overrightarrow {PA} \times \vec v \rVert\;\;\;\;\;\;\;\left[ 2 \right]\]
Igualando \(\left[ 1 \right]\) y \(\left[ 2 \right]\) podemos despejar \(d\):
\[\lVert \vec v\rVert.d = \lVert\overrightarrow {PA} \times \vec v\rVert\]
Ejemplo
Calcular la distancia entre la recta \(r:\left( {x,y,z} \right) = \left( {1,0, – 1} \right) + \lambda \left( { – 2,1,1} \right)\) y el punto \(A\left( {3, – 1,1} \right)\).
Resolución
Aplicamos la fórmula:
\[\;d\left( {A,r} \right) = \frac{{\lVert\overrightarrow {PA} \times \vec v\rVert}}{{\lVert\vec v\rVert}}\]
Tomamos un punto cualquiera de la recta, por ejemplo \(P\left( {1,0, – 1} \right)\) y formamos:
\[\overrightarrow {PA} = \left( {2, – 1,2} \right)\]
\[d\left( {A,r} \right) = \frac{{\lVert\left( {2, – 1,2} \right) \times \left( { – 2,1,1} \right)\rVert}}{{\;\lVert\left( { – 2,1,1} \right)\rVert}} = \frac{{\lVert\left( { – 3, – 6,0} \right)\rVert}}{{\sqrt 6 \;}} = \frac{{\sqrt {45} }}{{\sqrt 6 }} \cong 2,74\]
Distancia entre dos rectas paralelas
La fórmula que hemos visto permite calcular la distancia entre dos rectas paralelas. Veamos un ejemplo:
Dadas las rectas \({r_1}:\left( {x,y,z} \right) = \left( {1,0,0} \right) + t\left( {2, – 1,1} \right)\;\) y \({r_2}:\left\{ {\begin{array}{*{20}{c}}{y + z = 2}\\{x + ky = 0}\end{array}} \right.\)
Hallar \(k\) tal que \({r_1}\parallel {r_2}\) y calcular \(d\left( {{r_1},{r_2}} \right).\)
Recordemos la condición para que dos rectas sean paralelas:
\[{r_1}\parallel {r_2}\; \Leftrightarrow \overrightarrow {{v_1}} = \alpha \;\overrightarrow {{v_2}} \;\;\;\;\;\left[ 1 \right]\]
La recta \({r_2}\) está definida como intersección de dos planos. Si hacemos el producto vectorial de los vectores normales tendremos un vector director de la recta:
\[\left( {0,1,1} \right) \times \left( {1,k,0} \right) = \left( { – k,1, – 1} \right)\]
Por [1]:
\[\left( { – k,1, – 1} \right) = \alpha \left( {2, – 1,1} \right)\; \Rightarrow \;\left\{ {\begin{array}{*{20}{c}}{ – k = 2\alpha }\\{1 = – \alpha }\\{ – 1 = \alpha }\end{array}} \right.\;\]
\[ \Rightarrow k = 2\]
Para calcular la distancia, tomemos dos puntos cualesquiera de las rectas y construyamos el vector \(\overrightarrow {{P_1}{P_2}} \):
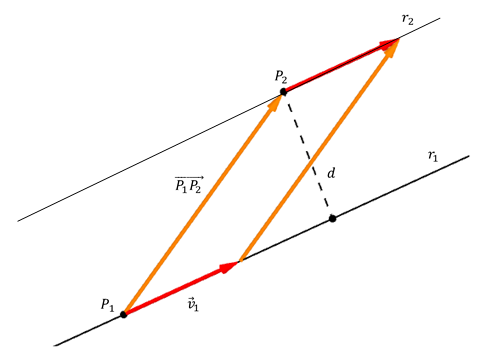
\[{P_1}\left( {1,0,0} \right) \in {r_1}\;\;\;,\;\;\;{P_2}\left( {0,0,2} \right) \in {r_2}\;\;\;,\;\;\;\overrightarrow {{P_1}{P_2}} = \left( { – 1,0,2} \right)\]
La distancia entre las rectas será la distancia entre \({P_2}\) y \({r_1}\):
\[d\left( {{r_1},{r_2}} \right) = d\left( {{P_2},{r_1}} \right) = \frac{{\overrightarrow {{P_1}{P_2}} \times \overrightarrow {{v_1}} }}{{\overrightarrow {{v_1}} }}\]
\[\overrightarrow {{P_1}{P_2}} \times {\vec v_1} = \left( { – 1,0,2} \right) \times \left( {2, – 1,1} \right) = \left( {2,5,1} \right)\]
\[\overrightarrow {{P_1}{P_2}} \times \vec v = \sqrt {30} \]
\[d\left( {{r_1},{r_2}} \right) = \frac{{\sqrt {30} }}{{\sqrt 6 }} = \sqrt 5 \]
Como ven, con las mismas herramientas resolvimos un problema diferente.
Distancia entre rectas alabeadas
Dadas dos rectas \({r_1}\) y \({r_2}\) no paralelas, nos proponemos calcular la distancia entre ambas:
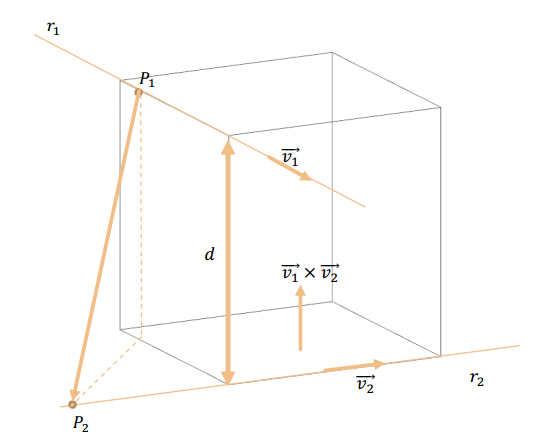
La mínima distancia entre dos rectas alabeadas \({r_1}\) y \({r_2}\) se obtiene al proyectar el vector \(\overrightarrow {{P_1}{P_2}} \) sobre la dirección perpendicular a ambas rectas, dada por \(\overrightarrow {{v_1}} \times \overrightarrow {{v_2}} \) :
\[d\left( {{r_1},{r_2}} \right) = {\lVert\overrightarrow {proy} _{\overrightarrow {{v_1}} \times \overrightarrow {{v_2}} }}\left( {\overrightarrow {{P_1}{P_2}} } \right)\rVert\]
Recordemos que:
\[\lVert{\overrightarrow {proy} _{\vec v}}\left( {\vec u} \right)\rVert = \frac{{\left| {\vec u.\vec v} \right|}}{{\lVert\vec v\rVert}}\]
Entonces podemos obtener una fórmula para la distancia entre \({r_1}\) y \({r_2}\):
¿Qué significa que la distancia dé \(0\)?
Condición de coplanaridad
Habíamos visto que tanto las rectas concurrentes como las paralelas son coplanares (existe un plano que las contiene).
-
Si las rectas se cortan, la distancia entre ellas es cero y por lo tanto:
\(\left( {\overrightarrow {{v_1}} \times \overrightarrow {{v_2}} } \right)\overrightarrow { \cdot {P_1}{P_2}} = 0\).
- Si las rectas son paralelas, \(\overrightarrow {{v_1}} \times \overrightarrow {{v_2}} = \vec 0\) y por lo tanto también se cumple que \(\left( {\overrightarrow {{v_1}} \times \overrightarrow {{v_2}} } \right)\overrightarrow { \cdot {P_1}{P_2}} = 0\).
Entonces estamos en condiciones de enunciar una condición de coplanaridad entre dos rectas:
Ejemplo
Dadas las rectas:
\[{r_1}:\left( {x,y,z} \right) = \left( {3,2,5} \right) + \lambda \left( {0, – 1,2} \right)\]
\[{r_2}\;:\left\{ {\begin{array}{*{20}{c}}{2x + y + 3z + 2 = 0}\\{ – x + 2y – 4z + 3 = 0}\end{array}} \right.\]
Calcular \(d\left( {{r_1},{r_2}} \right)\)
Resolución
Debemos verificar que se trata de rectas alabeadas. Busquemos la dirección de la recta \({r_2}\;\):
\[\overrightarrow {{v_2}} = \left( {2,1,3} \right) \times \left( { – 1,2, – 4} \right) = \left( { – 10,5,5} \right)\]
Vemos que las rectas no son paralelas porque sus vectores directores no son paralelos. Luego podemos utilizar la fórmula para distancia entre rectas alabeadas:
\[d\left( {{r_1},{r_2}} \right) = \frac{{\left| {\overrightarrow {{P_1}{P_2}} .\left( {\overrightarrow {{v_1}} \times \overrightarrow {{v_2}} } \right)} \right|}}{{\lVert\overrightarrow {{v_1}} \times \overrightarrow {{v_2}} \rVert}}\]
Para hallar\(\;\;{P_2}\; \in {r_2}\;\)fijamos \(z = 0\), por ejemplo, y averiguamos los valores de \(x\) e \(y\) resolviendo el sistema de ecuaciones:
\[\left\{ {\begin{array}{*{20}{c}}{2x + y + 2 = 0}\\{ – x + 2y + 3 = 0}\end{array}} \right.\;\; \Rightarrow \;\;x = – \frac{1}{5}\;\;\;,\;\;\;y = – \frac{8}{5}\;\]
Obtenemos así \({P_2}\left( { – \frac{1}{5}, – \frac{8}{5},0} \right) \in {r_2}\)
Calculamos:
\[\overrightarrow {{P_1}{P_2}} = \left( { – \frac{{16}}{5},\; – \frac{{18}}{5}, – 5} \right)\]
\[\overrightarrow {{v_1}} \times \overrightarrow {{v_2}} = \left( {0, – 1,2} \right) \times \left( { – 10,5,5} \right) = \left( { – 15,\; – 20, – 10} \right)\;\]
\[\lVert\overrightarrow {{v_1}} \times \overrightarrow {{v_2}}\rVert = \sqrt {{{\left( { – 15} \right)}^2} + {{\left( { – 20} \right)}^2} + {{\left( { – 10} \right)}^2}} = \sqrt {725} \]
\[\overrightarrow {{P_1}{P_2}} .\left( {\overrightarrow {{v_1}} \times \overrightarrow {{v_2}} } \right) = \left( { – \frac{{16}}{5},\; – \frac{{18}}{5}, – 5} \right).\left( { – 15, – 20, – 10} \right) = 48 + 72 + 50 = 170\]
\[d\left( {{r_1},{r_2}} \right) = \frac{{170}}{{\sqrt {725} }} \cong 6,31\]
Ejercicio para el lector 7
Dadas las rectas del ejemplo anterior:
\[{r_1}:\left( {x,y,z} \right) = \left( {3,2,5} \right) + \lambda \left( {0, – 1,2} \right)\]
\[{r_2}:\;\;\left\{ {\begin{array}{*{20}{c}}{2x + y + 3z + 2 = 0}\\{ – x + 2y – 4z + 3 = 0}\end{array}} \right.\]
Hallar la ecuación del plano \(\pi \) que contiene a \({r_1}\) y es paralelo a \(\;{r_2}\).
Ejercicio para el lector 8
Dadas las rectas \({r_1}\;:\left( {x,y,z} \right) = \;t\left( {1,1,2} \right)\) y \({r_2}:\;\;\left( {x,y,z} \right) = \left( {1,k,0} \right) + \;\lambda \;\left( {2,1,0} \right)\)
Hallar el valor de \(k\) para que las rectas sean coplanares y encontrar el plano que las contiene.

