Conjunto generador. LI y LD. Base. Dimensión.

Combinación lineal

Definición

Sean \({v_1},{v_2}, \ldots ,{v_r},w\) vectores de un espacio vectorial \(V\). Se dice que el vector \(w\;\)es una combinación lineal de los vectores \({v_1},\;{v_2},\; \ldots \;,\;{v_r}\) si se puede expresar como sigue:

\[w = {k_1}{v_1} + {k_2}{v_2} + \; \ldots + {k_r}{v_r}\;\;\]

donde \({k_1},\;{k_2},\; \ldots ,\;{k_r}\) son escalares.

Observación: Nosotros estamos trabajando con espacios vectoriales reales, o sea que los escalares son números reales.

Ejemplo 1

El vector \(\left( {0,0,3} \right)\) es combinación lineal de \(\left( {0,0,1} \right)\) ya que:

\[\left( {0,0,3} \right) = 3\left( {0,0,1} \right)\]

Veamos cómo se puede pensar esto desde la perspectiva geométrica. ¿Qué vectores pueden expresarse como combinación lineal del vector \(\left( {0,0,1} \right)\)?

Todos los vectores \(\left( {0,0,k} \right)\) con \(k \in \mathbb{R}\). Es decir que todos los vectores sobre el eje \(z\), son combinación lineal de \(\left( {0,0,1} \right)\).

Ejemplo 2

El vector \(\left( {1,0,4} \right)\) es combinación lineal de \(\left( {1,0,1} \right),\left( {0,0,2} \right)\) ya que:

\[1.\left( {1,0,1} \right) + \frac{3}{2}.\left( {0,0,2} \right) = \left( {1,0,4} \right)\]

Geométricamente el vector \(\left( {1,0,4} \right)\) es un vector coplanar con los vectores \(\left( {1,0,1} \right)\) y \(\left( {0,0,2} \right)\). Se puede ver en la siguiente gráfica que pertenecen al plano \(y = 0\):

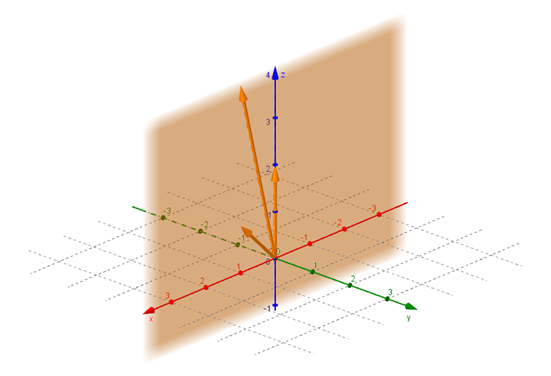
Ejemplo 3

El vector \(8x – 4{x^2}\) es combinación lineal de los vectores \(x\) y \({x^2}\) ya que:

\[8x – 4{x^2} = 8.\left( x \right) + \left( { – 4} \right).{x^2}\]

Ejemplo 4

¿Es el vector \(\left( {1,8} \right)\) combinación lineal de los vectores \(\left( {1,0} \right),\left( {3,3} \right)\)?

Para responder esto debemos buscar si existen escalares \(\alpha ,\beta \) tales que:

\[\left( {1,8} \right) = \alpha \left( {1,0} \right) + \beta \left( {3,3} \right)\]

\[\left\{ {\begin{array}{*{20}{c}}{1 = \alpha + 3\beta }\\{8 = 3\beta }\end{array}} \right. \Rightarrow \alpha = – 7,\;\;\;\beta = \frac{8}{3}\]

Como existen escalares que satisfacen la igualdad entonces \(\left( {1,8} \right)\) es combinación lineal de \(\left( {1,0} \right),\left( {3,3} \right)\).

Ejemplo 5

¿Para qué valores de k el vector \(\left( {1,2,3} \right)\) es combinación lineal de los vectores \(\left( {1,0,0} \right),\left( {0,1,0} \right),\left( {0,2,k} \right)\)?

Para responder esto debemos buscar si existen escalares \(\alpha ,\beta ,\gamma \) tales que:

\[\left( {1,2,3} \right) = \alpha \left( {1,0,0} \right) + \beta \left( {0,1,0} \right) + \gamma \left( {0,2,k} \right)\]

\[\left\{ {\begin{array}{*{20}{c}}{\alpha = 1}\\{\beta + 2\gamma = 2}\\{\gamma k = 3}\end{array}} \right.\;\]

Si \(k = 0\) la tercera ecuación queda \(0 = 3\), y el sistema es incompatible. Si \(k \ne 0\) entonces se puede obtener \(\gamma \;{\rm{y}}\;\beta \).

Entonces para todo \(k \ne 0\) el vector \(\left( {1,2,3} \right)\) se puede expresar como combinación lineal de los vectores dados.

Conjunto generador

Ejemplo 1

¿Es el conjunto \(\left\{ {\left( {1,1} \right),\left( {1, – 1} \right)} \right\}\) generador de \({\mathbb{R}^2}\)?

Siguiendo la definición, debemos ver si cualquier vector de \({\mathbb{R}^2}\) puede expresarse como combinación lineal de \(\left( {1,1} \right),\left( {1, – 1} \right)\):

\[\left( {x,y} \right) = \alpha \left( {1,1} \right) + \beta \left( {1, – 1} \right)\;\; \Rightarrow \;\;\left\{ {\begin{array}{*{20}{c}}{x = \alpha + \beta }\\{y = \alpha – \beta }\end{array}} \right.\; \Rightarrow \alpha = \frac{{x + y}}{2}\;\;,\;\;\;\beta = \frac{{x – y}}{2}\]

Hemos llegado a un sistema compatible determinado. Para cada \(x\) e \(y\) se obtrendrá un valor para \(\alpha \) y para \(\beta \).

Entonces, como cualquier vector \(\left( {x,y} \right)\) de \({\mathbb{R}^2}\) puede expresarse como combinación lineal de \(\left( {1,1} \right),\left( {1, – 1} \right)\), decimos que \(\left\{ {\left( {1,1} \right),\left( {1, – 1} \right)} \right\}\) es un conjunto generador de \({\mathbb{R}^2}\).

Ejemplo 2

¿Es el conjunto \(\left\{ {\left( {1,1} \right),\left( {1, – 1} \right),\left( {2,0} \right)} \right\}\) generador de \({\mathbb{R}^2}\)?

Otra vez planteamos un sistema de ecuaciones. Nos interesa saber si tiene solución o no:

\[\left( {x,y} \right) = \alpha \left( {1,1} \right) + \beta \left( {1, – 1} \right) + \gamma \left( {2,0} \right)\;\; \Rightarrow \;\;\left\{ {\begin{array}{*{20}{c}}{x = \alpha + \beta + 2\gamma }\\{y = \alpha – \beta }\end{array}} \right.\;\]

Veamos cómo es la resolución por el método de Gauss:

\[\left( {\begin{array}{*{20}{c}}1&1&2&x\\1&{–1}&0&y\end{array}} \right)\mathop  \to \limits_{{F_2} \to {F_2}–{F_1}} \left( {\begin{array}{*{20}{c}}1&1&2&x\\0&{–2}&{–2}&{y–x}\end{array}} \right)\mathop  \to \limits_{{F_2} \to –\frac{1}{2}.{F_2}} \left( {\begin{array}{*{20}{c}}1&1&2&x\\0&1&1&{\frac{{x–y}}{2}}\end{array}} \right)\]

\[\left\{ {\begin{array}{*{20}{c}}{\alpha + \beta + 2\gamma = x}\\{\beta + \gamma = \frac{{x – y}}{2}}\end{array}} \right. \Rightarrow \;\left\{ {\begin{array}{*{20}{c}}{\alpha = – \gamma + \frac{{x + y}}{2}}\\{\beta = \frac{{x – y}}{2} – \gamma }\end{array}} \right.\]

Para cada \(\left( {x,y} \right)\) en \({\mathbb{R}^2}\) , el sistema es compatible (indeterminado). Entonces \(\left\{ {\left( {1,1} \right),\left( {1, – 1} \right),\left( {2,0} \right)} \right\}\) también genera \({\mathbb{R}^2}\).

Ejemplo 3

¿Es el conjunto \(\left( {1,0,0} \right),\left( {0,1,0} \right),\left( {1,1,1} \right)\) generador de \({\mathbb{R}^3}\)?

\[\left( {x,y,z} \right) = \alpha \left( {1,0,0} \right) + \beta \left( {0,1,0} \right) + \gamma \left( {1,1,1} \right)\; \Rightarrow \;\left\{ {\begin{array}{*{20}{c}}{x = \alpha + \gamma }\\{y = \beta + \gamma }\\{z = \gamma }\end{array}} \right.\; \Rightarrow \;\left\{ {\begin{array}{*{20}{c}}{\alpha = x – z}\\{\beta = y – z}\\{\gamma = z}\end{array}} \right.\]

Como el sistema es compatible (determinado), podemos afirmar que el conjunto \(\left\{ {\left( {1,0,0} \right),\left( {0,1,0} \right),\left( {1,1,1} \right)} \right\}\) genera \({\mathbb{R}^3}\).

Ejemplo 4

¿Qué vectores pueden expresarse como combinación lineal del \(\left( {1,0} \right)\)?

Los vectores de la forma \(\left( {x,0} \right)\). Entonces el vector \(\left( {1,0} \right)\) no genera todo \({\mathbb{R}^2}\), pero genera la recta \(y = 0\).

Ejemplo 5

¿Qué vectores pueden expresarse como combinación lineal de \(\left( {1,0,0} \right)\) y \(\left( {0,1,0} \right)\)?

\[\left( {x,y,z} \right) = \alpha \left( {1,0,0} \right) + \beta \left( {0,1,0} \right) = \left( {\alpha ,\beta ,0} \right)\]

Es decir todos los vectores con componente \(z = 0\). Entonces \(\left( {1,0,0} \right)\) y \(\left( {0,1,0} \right)\) no generan \({\mathbb{R}^3}\) sino el plano \(z = 0\).

Subespacio generado

Sean \({v_1},\;{v_2},\; \ldots ,\;{v_r}\) vectores de un espacio vectorial \(V\).

1. El vector nulo puede expresarse como combinación lineal de dichos vectores:

\[{0_V}\; = \;0\;{v_1}\;\; + \;0\;{v_2}\; + \; \ldots \; + \;0{v_r}\]

2. Si sumamos dos combinaciones lineales de los vectores dados, obtenemos otra combinación lineal:

\[\left( {{a_1}{v_1}\; + \; \ldots \; + \;{a_r}{v_r}} \right) + \;\left( {{b_1}{v_1}\;\; + \; \ldots \; + \;{b_r}{v_r}} \right) = \;\left( {{a_1} + \;{b_1}} \right){v_1} + \ldots + \left( {\;{a_r} + {b_r}} \right){v_r}\]

3. Si multiplicamos un escalar k por una combinación lineal de los vectores dados, obtenemos una combinación lineal de dichos vectores:

\[k\;\left( {\;{a_1}\;{v_1}\; + \; \ldots \; + \;{a_r}\;{v_r}} \right)\; = \;\left( {k{a_1}} \right){v_1}\; + \; \ldots \; + \;\left( {k\;{a_r}} \right){v_r}\]

Estas tres condiciones permiten afirmar que el conjunto de todas las combinaciones lineales de \({v_1},\;{v_2},\; \ldots ,\;{v_r}\) es un subespacio de \(V\).

Entonces:

Ejemplo 1

Las combinaciones lineales del vector \(\left( {2,1} \right)\) son todos los vectores de la forma \(\left( {2k,k} \right)\) con \(k \in \mathbb{R}\).

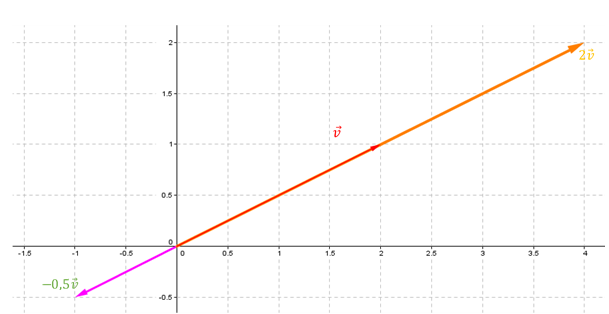
Geométricamente el subespacio generado por \(\left( {2,1} \right)\) es la recta que pasa por el origen y tiene la dirección de dicho vector.

Ejemplo 2

Las combinaciones lineales de los vectores \(\left( {1,0,2} \right),\left( {0,0,1} \right)\) son los vectores coplanares con \(\left( {1,0,2} \right)\) y \(\left( {0,0,1} \right)\):

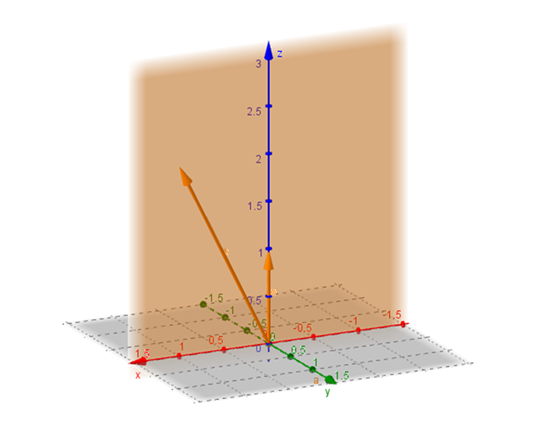
Veamos, analíticamente, cual es el espacio generado por \(\left( {1,0,2} \right),\left( {0,0,1} \right)\):

\[\left( {x,y,z} \right) = \alpha \left( {1,02} \right) + \beta \left( {0,0,1} \right) = \left( {\alpha ,0,2\alpha + \beta } \right)\;\;\;\;\;\;\;\alpha ,\beta \in \mathbb{R}\]

Son todos los vectores con segunda componente nula. Es decir que el subespacio generado es el plano \(y = 0\).

O sea: \(gen\left\{ {\;\left( {1,0,2} \right),\;\left( {0,0,1} \right)} \right\} = \left\{ {\;\left( {x,y,z} \right) \in {\mathbb{R}^3}\;:\;\;y = 0\;} \right\}\)

Ejemplo 3

Tomemos los vectores del ejemplo anterior: \(\left( {1,0,2} \right),\;\;\left( {0,0,1} \right)\) y además el vector\(\;\left( { – 1,0,1} \right)\).

¿Qué espacio generan?

\[\left( {x,y,z} \right) = \alpha \left( {1,02} \right) + \beta \left( {0,0,1} \right) + \gamma \left( { – 1,0,1} \right) = \left( {\alpha – \gamma \;,\;0\;,\;2\alpha + \beta + \gamma } \right)\]

Son vectores con segunda componente nula. Se genera el mismo subespacio que en el ejemplo anterior. Esto se explica porque el tercer vector es coplanar con los primeros dos.

Independencia lineal y dependencia lineal

En los ejemplos 1 y 2 (de Conjunto generador) vimos que los conjuntos \(\left\{ {\;\left( {1,1} \right)\;,\;\left( {1, – 1} \right)\;} \right\}\;\;y\;\left\{ {\;\left( {1,1} \right)\;,\;\left( {1, – 1} \right)\;,\;\left( {2,0} \right)\;} \right\}\) generan \({\mathbb{R}^2}\). Si tuviéramos que elegir uno de ellos como generador de \({\mathbb{R}^2}\), ¿por cuál nos inclinaríamos?

El problema de encontrar los conjuntos generadores más «pequeños» para un espacio vectorial depende de la noción de independencia lineal, que presentamos en esta sección.

Una forma alternativa de caracterizar la dependencia lineal es la siguiente:

Demostración:

\(\Rightarrow\) Si el conjunto \(\left\{ {\;{v_1},{v_2},\; \ldots ,{v_r}\;} \right\}\) es linealmente dependiente, la ecuación

\[{\alpha _1}{v_1} + {\alpha _2}{v_2} + \; \ldots + \;{\alpha _r}{v_r} = {0_V}\]

admite otras soluciones además de la trivial. O sea, existe una combinación lineal donde al menos uno de los escalares es distinto de cero, que da el vector nulo.

Supongamos que \({\alpha _1} \ne 0\). Entonces resulta:

\[{v_1} = \left( { – \frac{{{\alpha _2}}}{{{\alpha _1}}}} \right){v_2} + \ldots + \left( { – \frac{{{\alpha _r}}}{{{\alpha _1}}}} \right){v_r}\]

Por lo tanto, el vector \({v_1}\) es combinación lineal de los demás.

\(\Leftarrow\) Sabemos que uno de los vectores puede expresarse como combinación de los demás. Sin perder generalidad, supongamos que:

\[{\color{red}{v_1}} = {k_2}{v_2} + \ldots + {k_r}{v_r}\]

Entonces:

\[ – 1{\color{red}{v_1}} + {k_2}{v_2} + \ldots + {k_r}{v_r} = {0_V}\]

Existe una combinación lineal no trivial (al menos uno de los escalares es distinto de cero) que es igual al vector nulo. Por lo tanto, el conjunto \(\left\{ {\;{v_1},{v_2},\; \ldots ,{v_r}\;} \right\}\) es linealmente dependiente, como queríamos demostrar.

Ejemplo 1

¿Es el conjunto \(\left\{ {\left( {1,1} \right),\left( {1, – 1} \right)} \right\}\) linealmente independiente (LI) o linealmente dependiente (LD)?

Planteamos la ecuación:

\[{\alpha _1}\left( {1,1} \right) + {\alpha _2}\left( {1, – 1} \right) = \left( {0,0} \right)\]

\[\left\{ {\begin{array}{*{20}{c}}{{\alpha _1} + {\alpha _2} = 0}\\{{\alpha _1} – {\alpha _2} = 0}\end{array}} \right.\;\;\;\; \Rightarrow \;\;\;\;{\alpha _1} = 0 \wedge {\alpha _2} = 0\]

Luego el conjunto es linealmente independiente (LI).

Ejemplo 2

¿Es el conjunto \(\left\{ {\left( {1,1} \right),\left( {1, – 1} \right),\left( {2,0} \right)} \right\}\) LI o LD?

Planteamos un sistema de ecuaciones. Nos interesa saber si tiene solución única o infinitas soluciones:

\[\alpha \left( {1,1} \right) + \beta \left( {1, – 1} \right) + \gamma \left( {2,0} \right) = \left( {0,0} \right)\;\;\; \Rightarrow \;\left\{ {\begin{array}{*{20}{c}}{0 = \alpha + \beta + 2\gamma }\\{0 = \alpha – \beta }\end{array}} \right.\;\]

Veamos cómo es la resolución por el método de Gauss:

\[\left( {\begin{array}{*{20}{c}}1&1&2&0\\1&{ – 1}&0&0\end{array}} \right)\mathop \to \limits_{{F_2} \to {F_1} – {F_2}} \left( {\begin{array}{*{20}{c}}1&1&2&0\\0&{ – 2}&{ – 2}&0\end{array}} \right)\mathop \to \limits_{{F_2} \to – \frac{1}{2}.{F_2}} \left( {\begin{array}{*{20}{c}}1&1&2&0\\0&1&1&0\end{array}} \right)\]

\[\left\{ {\begin{array}{*{20}{c}}{\alpha + \beta + 2\gamma = 0}\\{\beta + \gamma = 0}\end{array}} \right. \Rightarrow \;\left\{ {\begin{array}{*{20}{c}}{\alpha = – \gamma }\\{\beta = – \gamma }\end{array}} \right.\]

El sistema de ecuaciones es compatible indeterminado, o sea tiene infinitas soluciones. Luego, el conjunto es LD.

Notemos que también se cumple la forma alternativa de caracterizar la dependencia lineal, pues es posible escribir \(\left( {2,0} \right)\) como combinación lineal de \(\left( {1,1} \right)\) y \(\left( {1, – 1} \right)\):

\[\left( {1,1} \right) + \left( {1, – 1} \right) = \left( {2,0} \right)\]

Ejemplo 3

¿Es el conjunto \(\left\{ {\left( {1,0,0} \right),\left( {0,1,0} \right),\left( {1,1,1} \right)} \right\}\) LI o LD?

\[\alpha \left( {1,0,0} \right) + \beta \left( {0,1,0} \right) + \gamma \left( {1,1,1} \right) = \left( {0,0,0} \right)\; \Rightarrow \;\left\{ {\begin{array}{*{20}{c}}{0 = \alpha + \gamma }\\{0 = \beta + \gamma }\\{0 = \gamma }\end{array}} \right.\; \Rightarrow \;\left\{ {\begin{array}{*{20}{c}}{\alpha = 0}\\{\beta = 0}\\{\gamma = 0}\end{array}} \right.\]

Como el sistema es compatible determinado, el conjunto es LI.

Ejemplo 4

¿Es el conjunto \(\left\{ {\;\left( {1,0,0} \right)\;,\;\left( {0,1,0} \right)} \right\}\) LI o LD?

\[\alpha \left( {1,0,0} \right) + \beta \left( {0,1,0} \right) = \left( {0,0,0} \right)\;\; \Rightarrow \;\;\;\;\left\{ {\begin{array}{*{20}{c}}{\alpha = 0}\\{\beta = 0}\end{array}} \right.\]

Como el sistema tiene solución única el conjunto es LI.

Ejemplo 5

¿Es el conjunto \(\left\{ {\color{green}{x}\;\;,\;\;\; \color{red}{- {x^2}}\;\;\;\;,\;\;\;\;\color{fuchsia}{4{x^2} – x}} \right\}\) LI o LD?

\[{\alpha _1}\left( \color{green}{x} \right) + {\alpha _2}\left( { \color{red}{- {x^2}}} \right) + {\alpha _3}\left( {\color{fuchsia}{4{x^2} – x}} \right) = 0{x^2} + 0x + 0\]

\[\left\{ {\begin{array}{*{20}{c}}{ – {\alpha _2} + 4{\alpha _3} = 0}\\{{\alpha _1} – {\alpha _3} = 0}\end{array}} \right. \Rightarrow \;\;\;\;\left\{ {\begin{array}{*{20}{c}}{{\alpha _2} = 4{\alpha _3}}\\{{\alpha _1} = {\alpha _3}}\end{array}} \right.\]

El sistema es compatible indeterminado. Luego el conjunto es LD.

Notemos que es posible escribir \(\color{fuchsia}{4{x^2} – x}\) cómo combinación lineal de \(\color{green}{x}\) y de \( \color{red}{- {x^2}}\):

\[\left( { – 1} \right)\left( \color{green}{x} \right) + \left( { – 4} \right)\left( { \color{red}{- {x^2}}} \right) = \color{fuchsia}{4{x^2} – x}\]

Propiedades

Propiedad 1

Un conjunto formado por un solo vector, ¿es linealmente independiente (LI) o dependiente (LD)?

Planteamos la combinación lineal:

\[\alpha \;v = {0_V}\]

Si \(v = {0_V}\), \(\alpha \) puede tomar cualquier valor. Por lo tanto: \(\left\{ {{0_V}} \right\}\) es LD.

Si \(v \ne {0_V}\) , la única solución es \(\alpha = 0\). Por lo tanto: \(\left\{ v \right\}\) es LI.

Propiedad 2

Si un conjunto de vectores contiene al vector nulo, entonces es linealmente dependiente (LD).

Demostración:

Sea \(A = \left\{ {{v_1},\;{v_2},\; \ldots ,\;{v_r},\;{0_V}} \right\} \subset V\)

Entonces se tiene que:

\[0{v_1} + 0{v_2} + \ldots + 0{v_r} + 1\;{0_V} = {0_V}\]

Probamos que existe una combinación lineal con escalares no todos nulos, que da el vector nulo. Por lo tanto, \(A\) es linealmente dependiente.

Interpretación geométrica

Observación previa: En lo que sigue consideramos los vectores colocados a partir del origen de coordenadas.

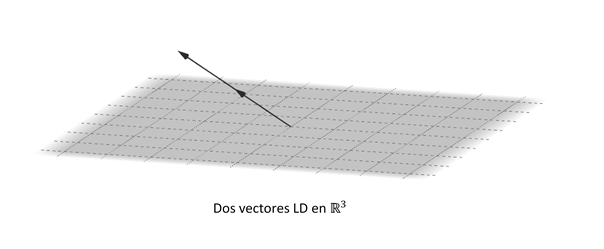
De [1] resulta que dos vectores \({v_1}\) y \({v_2}\) son linealmente dependientes (LD) si y sólo si uno de ellos es un múltiplo escalar del otro.

Podemos afirmar entonces que dos vectores en \({\mathbb{R}^2}\) o \({\mathbb{R}^3}\) son LD si y sólo si están sobre la misma recta que pasa por el origen (vectores paralelos).

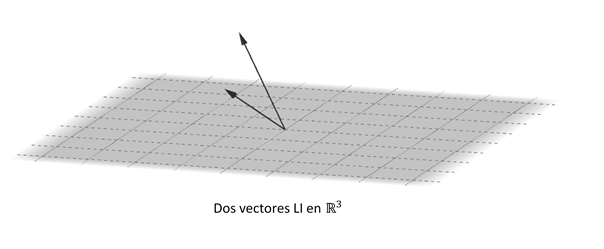
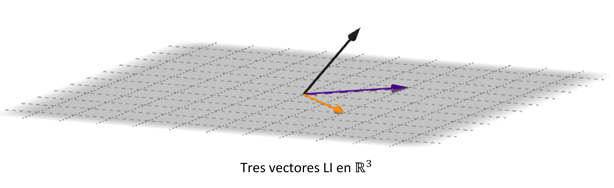
En \({\mathbb{R}^3}\), tres vectores \({v_1},\;{v_2},\;{v_3}\) son LD si y sólo si están situados en el mismo plano que pasa por el origen (vectores coplanares).

Base y dimensión de un espacio vectorial

Habíamos visto que los conjuntos \(B = \left\{ {\left( {1,\;1} \right),\;\left( {1,\; – 1} \right)} \right\}\) y \(C = \left\{ {\left( {1,\;1} \right),\;\left( {1,\; – 1} \right),\;\left( {2,\;0} \right)} \right\}\) generan \({\mathbb{R}^2}.\) ¿Cuál es la diferencia entre ellos?

\(B\) es un conjunto linealmente independiente, en cambio \(C\) es linealmente dependiente porque \(\left( {2,\;0} \right) = \left( {1,\;1} \right) + \left( {1,\; – 1} \right)\).

Teniendo en cuenta esta definición, \(B = \left\{ {\left( {1,\;1} \right),\;\left( {1,\; – 1} \right)} \right\}\) es una base de \({\mathbb{R}^2}\). Otra base de \({\mathbb{R}^2}\) muy usual es la que contiene a los versores canónicos: \(E = \left\{ {\left( {1,\;0} \right)\;,\;\left( {0,\;1} \right)} \right\}\).

Observamos que las dos bases están compuestas por dos vectores linealmente independientes. ¿Será ésta una característica de cualquier base de \({\mathbb{R}^2}\)?

Puede demostrarse que:

Si \(B\; = \;\left\{ {{v_1},\;{v_2},\; \ldots ,\;{v_n}} \right\}\) es una base de \(V\), entonces todo conjunto con más de n vectores es linealmente dependiente.

De acuerdo con esta propiedad, podemos deducir una característica común a toda base de un espacio vectorial:

Sean \(B = \left\{ {{v_1},{v_2},\; \ldots ,\;{v_n}} \right\}\) y \(B’ = \left\{ {{w_1},\;{w_2},\; \ldots ,\;{w_q}} \right\}\) dos bases del espacio vectorial \(V\).

Como \(B\) es una base, todo conjunto de más de \(n\) vectores es LD. Pero \(B’\) es LI, entonces:
\[q \le n\;\;\;\;\;\left[ 1 \right]\]

Como \(B’\) es una base, todo conjunto de más de \(q\) vectores es LD. Pero \(B\) es LI, entonces:

\[n \le q\;\;\;\;\;\left[ 2 \right]\]

De [1] y [2] se deduce que \(q = n\).

En consecuencia:

Si \(B = \left\{ {{v_1},{v_2}, \ldots ,\;{v_n}} \right\}\) es una base de \(V\), cualquier otra base de \(V\) tiene \(n\) vectores. Esto permite definir el concepto de dimensión.

Si no existe una base de \(V\) formada por un conjunto finito de vectores, se dice que \(V\) es un espacio de dimensión infinita. Un ejemplo es el espacio de todos los polinomios (de cualquier grado).

Como el vector nulo es linealmente dependiente, el espacio \(\left\{ {{0_V}} \right\}\) no tiene base. A este espacio compuesto únicamente por el vector nulo, se le asigna dimensión cero:

\[\dim \left( {\;\left\{ {{0_V}} \right\}\;} \right) = 0\]

Para determinar la dimensión de un espacio vectorial, es suficiente hallar una base de dicho espacio. Veamos qué dimensión tienen los espacios vectoriales con los cuales trabajaremos:

En \({\mathbb{R}^2}\) conocemos la base canónica:

\[{E_2} = \left\{ {\left( {1,0} \right),\left( {0,1} \right)} \right\}\; \Rightarrow \dim \left( {{\mathbb{R}^2}} \right) = 2\]

En \({\mathbb{R}^3}\) la base canónica es:

\[{E_3} = \left\{ {\left( {1,0,0} \right),\left( {0,1,0} \right),\left( {0,0,1} \right)} \right\} \Rightarrow \dim \left( {{\mathbb{R}^3}} \right) = 3\]

Análogamente en \({\mathbb{R}^4}\):

\[{E_4} = \left\{ {\left( {1,0,0,0} \right),\left( {0,1,0,0} \right),\left( {0,0,1,0} \right),\left( {0,0,0,1} \right)} \right\} \Rightarrow \dim \left( {{\mathbb{R}^4}} \right) = 4\]

De acuerdo con el número de vectores que componen cada una de estas bases, podemos afirmar que:

\[\dim \left( {{\mathbb{R}^n}} \right) = n\]

Para determinar la dimensión de los espacios de matrices, consideremos por ejemplo \(V = {\mathbb{R}^{3 \times 2}}\). Cualquier matriz de \(3 \times 2\) puede expresarse como sigue:

\[\left( {\begin{array}{*{20}{c}}a&b\\c&d\\e&f\end{array}} \right) = a\left( {\begin{array}{*{20}{c}}1&0\\0&0\\0&0\end{array}} \right) + b\left( {\begin{array}{*{20}{c}}0&1\\0&0\\0&0\end{array}} \right) + c\left( {\begin{array}{*{20}{c}}0&0\\1&0\\0&0\end{array}} \right) + d\left( {\begin{array}{*{20}{c}}0&0\\0&1\\0&0\end{array}} \right) + e\left( {\begin{array}{*{20}{c}}0&0\\0&0\\1&0\end{array}} \right) + f\left( {\begin{array}{*{20}{c}}0&0\\0&0\\0&1\end{array}} \right)\]

Observemos la similitud con \({\mathbb{R}^6}\) , sólo cambia el formato.

Encontramos seis matrices linealmente independientes que generan \(V = {\mathbb{R}^{3 \times 2}}\). Es decir, encontramos una base (llamada base canónica) de este espacio y por lo tanto: \(\dim \left( {{\mathbb{R}^{3×2}}} \right) = 3×2 = 6\).

Generalizando, podemos afirmar que:

\[\dim \left( {{\mathbb{R}^{mxn}}} \right) = mxn\]

Busquemos la dimensión de los espacios de polinomios. Consideremos por ejemplo \(V = {P_{2\;}}\). Cualquier polinomio de \({P_2}\) puede expresarse cómo sigue:

\[\;p\left( x \right) = {a_0} + {a_1}x + {a_2}{x^2} = {a_0}\color{red}{1} + {a_1}\color{red}{x} + {a_2}{\color{red}{x^2}}\]

El conjunto \(\left\{ {1,x,{x^2}} \right\}\) genera \({P_2}\) y además es linealmente independiente. Hemos obtenido una base (llamada canónica) de \({P_2}\), y por lo tanto \(\dim \left( {{P_2}} \right) = 3\).

Análogamente:

\[\left\{ {1,x,{x^2},{x^3}} \right\}\;\;base\;canó nica\;de\;{P_3}\]

\[\left\{ {1,x,{x^2},{x^3}, \ldots ,\;{x^n}} \right\}\;base\;canó nica\;de\;{P_n}\]

Entonces:

\[\dim \left( {{P_n}} \right) = n + 1\]

Ejemplo 1

Existen diferentes bases para un mismo espacio vectorial. Consideremos en \({\mathbb{R}^2}\) el conjunto:
\[B = \left\{ {\left( {1,0} \right),\left( {1,1} \right)} \right\}\]

Es fácil ver que \(B\) es linealmente independiente (sólo la combinación lineal trivial produce el vector nulo). Nos falta probar que genera \({\mathbb{R}^2}\).

\[\left( {x,y} \right) = \alpha \left( {1,0} \right) + \beta \left( {1,1} \right)\]

\[\left\{ {\begin{array}{*{20}{c}}{\alpha + \beta = x}\\{\beta = y}\end{array}} \right. \Rightarrow \alpha = x – y\;\; \wedge \;\;\beta = y\]

Para cualquier \(\left( {x,y} \right)\) en \({\mathbb{R}^2}\) es posible encontrar los escalares \(\alpha \) y \(\beta \). Probamos que \(B\) genera \({\mathbb{R}^2}\).

Entonces \(B = \left\{ {\left( {1,0} \right),\left( {1,1} \right)} \right\}\) es una base de \({\mathbb{R}^2}\).

Ejemplo 2

Hemos visto en ejemplos anteriores que el conjunto \(\left\{ {\left( {1,0,0} \right),\left( {0,1,0} \right),\left( {1,1,1} \right)} \right\}\) genera \({\mathbb{R}^3}\), y que son vectores LI. Por lo tanto es una base de \({\mathbb{R}^3}\).

Ejemplo 3

Veamos que el conjunto \(B = \left\{ {1,1 + x,1 + {x^2}} \right\}\) es una base de \({P_2}\).

Para esto debemos probar las dos condiciones.

Probemos que \(B\) es LI:

\[0 + 0x + 0{x^2} = \alpha \;1 + \beta \left( {1 + x} \right) + \gamma \left( {1 + {x^2}} \right) \Rightarrow \;\;\left\{ {\begin{array}{*{20}{c}}{\alpha + \beta + \gamma = 0}\\{\beta = 0}\\{\gamma = 0}\end{array}} \right.\;\; \Rightarrow \;\;\alpha = \beta = \gamma = 0\]

Cómo la única solución es la trivial, entonces el conjunto es LI.

Probemos que genera \({P_2}\):

\[a + bx + c{x^2} = \alpha \;1 + \beta \left( {1 + x} \right) + \gamma \left( {1 + {x^2}} \right) \Rightarrow \;\;\left\{ {\begin{array}{*{20}{c}}{\alpha + \beta + \gamma = a}\\{\beta = b}\\{\gamma = c}\end{array}} \right.\;\; \Rightarrow \;\left\{ {\begin{array}{*{20}{c}}{\alpha = a – b – c}\\{\beta = b}\\{\gamma = c}\end{array}} \right.\;\;\;\;\]

El sistema es compatible. Entonces para cualquier polinomio en \({P_2}\) es posible hallar los escalares \(\alpha ,\beta ,\gamma \). Luego \(B\) genera \({P_2}\).

Propiedades relacionadas con la dimensión

Si \(\dim \left( V \right) = n\) , puede afirmarse que:

1) Todo conjunto de \(n\) vectores linealmente independientes en \(V\) es una base.

2) Todo conjunto de \(n\) vectores que genere \(V\) es una base.

3) Todo conjunto de más de \(n\) vectores en el espacio vectorial \(V\) es linealmente dependiente.

4) Todo conjunto linealmente independiente en \(V\) puede extenderse a una base.

Ejemplo 1

¿Es el conjunto \(A = \left\{ {\left( {1,1,0} \right),\left( {2, – 1,1} \right),\left( {0,1,0} \right)} \right\}\) base de \({\mathbb{R}^3}\)?

Cómo \(\dim \left( {{\mathbb{R}^3}} \right) = 3\) y \(A\) tiene tres vectores, entonces por la propiedad 1, es suficiente probar que \(A\) es LI para asegurar que es una base de \({\mathbb{R}^3}\).

En \({\mathbb{R}^3}\), tres vectores \({v_1},\;{v_2},\;{v_3}\) son LD si y sólo si están situados en el mismo plano que pasa por el origen (vectores coplanares). Veamos si son coplanares haciendo el producto mixto:

\[\left( {1,1,0} \right).\left( {2, – 1,1} \right) \times \left( {0,1,0} \right) = \left| {\begin{array}{*{20}{c}}1&1&0\\2&{ – 1}&1\\0&1&0\end{array}} \right| = – 1 \ne 0\]

No son coplanares, por lo tanto son LI.

Luego \(A\) es base de \({\mathbb{R}^3}\).

Ejemplo 2

\[C = \left\{ {1 + x + {x^2},3 – x,2 + k{x^2}} \right\} \subset {P_2}\]

Determinar todos los \(k \in \mathbb{R}\) tales que \(C\) sea una base de \({P_2}\).

\(\dim \left( {{P_2}} \right) = 3\) \(\; \Rightarrow \;\) Todo conjunto de tres vectores L.I. en \({P_2}\) es base.

\[\alpha \left( {1 + x + {x^2}} \right) + \beta \left( {3 – x} \right) + \gamma \left( {2 + k{x^2}} \right) = {0_{{P_2}}}\]

Igualando coeficientes, resulta:

\[\left\{ {\begin{array}{*{20}{c}}{\alpha + 3\beta + 2\gamma = 0}\\{\alpha – \beta = 0}\\{\alpha + k\gamma = 0}\end{array}} \right.\]

Como es un sistema homogéneo, siempre tiene solución. ¿Buscamos que tenga solución única, o infinitas?

Buscamos los valores de \(k\) para que la única solución sea la trivial: \(\alpha = \beta = \gamma = 0\).

Habíamos visto que en los sistemas cuadrados homogéneos, el determinante de la matriz de coeficientes permite decidir si son SCD o SCI.

En este caso, \(A = \left( {\begin{array}{*{20}{c}}1&3&2\\1&{ – 1}&0\\1&0&k\end{array}} \right)\) y \(\det \left( A \right) = 2 – 4k\)

Si \(k = \frac{1}{2}\) el sistema queda compatible indeterminado.

Para cualquier \(k \ne \frac{1}{2}\;\) el sistema es compatible determinado, por lo tanto \(\left\{ {1 + x + {x^2},3 – x,2 + k{x^2}} \right\}\) es LI, y entonces es base de \({P_2}\).

Ejemplo 3

Dado \(A = \left\{ {{v_1},{v_2},{v_3},{v_4}} \right\} \subset {\mathbb{R}^3}\;\) puede afirmarse que este conjunto es LD. Si hubiera tres vectores LI, éstos formarían una base de \({\mathbb{R}^3}\)y por lo tanto el vector restante podría expresarse como combinación lineal de ellos.

Ejemplo 4

El conjunto \(\left\{ {u = \left( {1,2,3} \right),v = \left( {1,1,0} \right)} \right\}\) es LI en \({\mathbb{R}^3}\) pero no genera todo \({\mathbb{R}^3}\) sino que genera un plano. Podemos extenderlo a una base agregando algún vector LI, podría ser por ejemplo el producto vectorial entre estos dos. Obtenemos \(\left\{ {u,v,u \times v} \right\}\) que es una base de \({\mathbb{R}^3}\).

Coordenadas de un vector respecto de una base

Propiedad: Si \(B = \left\{ {{v_1},{v_2}, \ldots ,{v_n}} \right\}\) es una base del espacio vectorial \(V\), todo vector de \(V\;\)puede expresarse de forma única como combinación lineal de los vectores de B.

Demostración:

Sea \(B = \left\{ {{v_1},{v_2}, \ldots ,{v_n}} \right\}\) base de \(V\).

Supongamos que un vector \(u \in V\) puede expresarse mediante dos combinaciones lineales distintas de los vectores de la base B:

\(u = {\alpha _1}{v_1} + {\alpha _2}{v_2} + \ldots + {\alpha _n}{v_n}\) y \(u = {\beta _1}{v_1} + {\beta _2}{v_2} + \ldots + {\beta _n}{v_n}\)

Restando miembro a miembro, se obtiene:

\[{0_V} = ({\alpha _1} – {\beta _1})\;{v_1} + ({\alpha _2} – {\beta _2})\;{v_2} + \ldots + ({\alpha _n} – {\beta _n})\;{v_n}\]

Como las bases son conjuntos linealmente independientes, resulta:

\[{\alpha _i} – {\beta _i} = 0\;\;\;\left( {i = 1,\; \ldots ,\;n} \right)\]

Por lo tanto, los escalares de la combinación lineal son únicos para cada vector de V.

Esta propiedad permite definir coordenadas de un vector respecto de una base.

Indicaremos las coordenadas mediante la siguiente notación:
\[{\left[ u \right]_B} = \left( {\begin{array}{*{20}{c}}{{\alpha _1}}\\{\begin{array}{*{20}{c}}{{\alpha _2}}\\ \vdots \\{{\alpha _n}}\end{array}}\end{array}} \right)\]

Ejemplo 1

Sean,

\[B = \left\{ {\left( {1,0,0} \right),\left( {1,1,0} \right),\left( {2,2,1} \right)} \right\}\;base\;de\;{\mathbb{R}^3}\]

\[u = \left( { – 1,4,3} \right)\]

a) Hallar:

• \({\left[ u \right]_B}\) , coordenadas del vector \(u\) en la base \(B\)
• \({\left[ u \right]_E}\) , coordenadas del vector \(u\) en la base canónica

b) Sabiendo que:

\[{\left[ v \right]_B} = \left( {\begin{array}{*{20}{c}}3\\{\begin{array}{*{20}{c}}1\\2\end{array}}\end{array}} \right)\]

Hallar \(v\).

Resolución

Ítem a

\[\alpha \left( {1,0,0} \right) + \beta \left( {1,1,0} \right) + \gamma \left( {2,2,1} \right) = \left( { – 1,4,3} \right)\]

\[\left\{ {\begin{array}{*{20}{c}}{\alpha + \beta + 2\gamma = – 1}\\{\beta + 2\gamma = 4}\\{\gamma = 3}\end{array}} \right.\;\;\; \Rightarrow \;\;\;\left\{ {\begin{array}{*{20}{c}}{\alpha = – 5}\\{\beta = – 2}\\{\gamma = 3}\end{array}} \right.\]

Estos escalares son las coordenadas de \(u\) es la base \(B\):

\[{\left[ u \right]_B} = \left( {\begin{array}{*{20}{c}}{ – 5}\\{\begin{array}{*{20}{c}}{ – 2}\\3\end{array}}\end{array}} \right)\]

En el caso de la base canónica, las coordenadas del vector coinciden con sus componentes, ya que:

\[\left( {x,y,z} \right) = x\left( {1,0,0} \right) + y\left( {0,1,0} \right) + z\left( {0,0,1} \right)\]

Entonces:

\[{\left[ u \right]_E} = \left( {\begin{array}{*{20}{c}}{ – 1}\\{\begin{array}{*{20}{c}}4\\3\end{array}}\end{array}} \right)\]

Ítem b

Dadas una base y las coordenadas de un vector en esa base, podemos hallar el vector:

\[v = 3\left( {1,0,0} \right) + 1\left( {1,1,0} \right) + 2\left( {2,2,1} \right) = \left( {8,5,2} \right)\]

Observación: Las bases son conjuntos ordenados. O sea, si reordenamos los vectores de una base, obtenemos una base diferente. Así:

\(B = \left\{ {\left( {1,0,0} \right),\left( {1,1,0} \right),\left( {2,2,1} \right)} \right\}\) y \(B’ = \left\{ {\left( {2,2,1} \right),\left( {1,0,0} \right),\left( {1,1,0} \right)} \right\}\) son bases distintas de \({\mathbb{R}^3}\).

¿Por qué son distintas? Porque las coordenadas de un vector cambian si se reordena la base. Por ejemplo para \(u = \left( { – 1,4,3} \right)\) las coordenadas en cada base son:

\[{\left[ u \right]_B} = \left( {\begin{array}{*{20}{c}}{ – 5}\\{\begin{array}{*{20}{c}}{ – 2}\\3\end{array}}\end{array}} \right)\;\;\;\;\;\;\;\;y\;\;\;\;\;\;\;\;{\left[ u \right]_{B’}} = \left( {\begin{array}{*{20}{c}}3\\{\begin{array}{*{20}{c}}{ – 5}\\{ – 2}\end{array}}\end{array}} \right)\]

Ejemplo 2

Dados los vectores de \({\mathbb{R}^2}\), y sus coordenadas en la base \(B\):

\[u = \left( {5,2} \right)\;\;,\;\;\;v = \left( {7,1} \right)\]

\[{\left[ u \right]_B} = \left( {\begin{array}{*{20}{c}}3\\2\end{array}} \right)\;\;,\;\;\;\;{\left[ v \right]_B} = \left( {\begin{array}{*{20}{c}}5\\3\end{array}} \right)\]

Hallar, si es posible, la base \(B\).

Resolución

Una base \(B\) de \({\mathbb{R}^2}\) tiene dos vectores:

\[B = \left\{ {{v_1},{v_2}} \right\}\]

\[{\left[ u \right]_B} = \left( {\begin{array}{*{20}{c}}3\\2\end{array}} \right)\;\; \Rightarrow \;\;\;3{v_1} + 2{v_2} = \left( {5,2} \right)\]

\[{\left[ v \right]_B} = \left( {\begin{array}{*{20}{c}}5\\3\end{array}} \right)\; \Rightarrow \;\;\;5{v_1} + 3{v_2} = \left( {7,1} \right)\]

Entonces podemos resolverlo como un sistema de ecuaciones vectorial:

\[\left\{ {\begin{array}{*{20}{c}}{\;3{v_1} + 2{v_2} = \left( {5,2} \right)}\\{5{v_1} + 3{v_2} = \left( {7,1} \right)}\end{array}\;\;\; \Rightarrow \;\;\;\left\{ {\begin{array}{*{20}{c}}{15{v_1} + 10{v_2} = \left( {25,10} \right)}\\{15{v_1} + 9{v_2} = \left( {21,3} \right)}\end{array}} \right.} \right.\]

Restando las ecuaciones, se obtiene:

\[{v_2} = \left( {4,7} \right)\]

Sustituyendo y despejando, resulta: \({v_1} = \left( { – 1, – 4} \right)\).

Entonces

\[B = \left\{ {\left( { – 1, – 4} \right),\left( {4,7} \right)} \right\}\]

Base y dimensión de un subespacio vectorial

Recordemos que un subespacio es un espacio vectorial en sí mismo, por lo tanto podemos hallar una base y su dimensión.

Si S es un subespacio de V, entonces: \({\rm{dim}}\left( S \right) \le {\rm{dim}}\left( V \right)\).

Veamos cuáles son las dimensiones de los distintos tipos de subespacios de \({\mathbb{R}^3}\):

• \(\left\{ {\left( {0,0,0} \right)} \right\}\)
• Rectas que pasan por el origen,
• Planos que pasan por el origen y
• \({\mathbb{R}^3}\)

Sabemos que \({\mathbb{R}^3}\) tiene dimensión 3.

\(S = \left\{ {\left( {0,0,0} \right)} \right\}\) no tiene base y como habíamos dicho, se le asigna dimensión 0.

\[\dim \left( {\left\{ {{0_V}} \right\}} \right)\; = 0\]

Consideremos un plano que pase por el origen, por ejemplo:

\[\pi :\;\;x + 3y – 2z = 0\]

\[x = – 3y + 2z\]

\[\left( {x,y,z} \right) \in \pi \Leftrightarrow \left( {x,y,z} \right) = \left( { – 3y + 2z,y,z} \right) = \left( { – 3y,y,0} \right) + \left( {2z,0,z} \right) = y\left( { – 3,1,0} \right) + z\left( {2,0,1} \right)\]

Esto quiere decir que cualquier vector en ese plano se puede escribir como combinación lineal de \(\left( { – 3,1,0} \right)\) y \(\left( {2,0,1} \right)\). Cómo son LI:

\[\left\{ {\left( { – 3,1,0} \right),\left( {2,0,1} \right)} \right\}\;es\;una\;base\;de\;{S_1}\]

\[\dim \left( {{S_1}} \right) = 2\]

Los planos que pasan por el origen son subespacios de dimensión 2.

Ahora consideremos el subespacio:

\[{S_2} = \left\{ {\left( {x,y,z} \right) \in {\mathbb{R}^3}|\;\;x + y = 0\;\;\;,\;\;\;\;x – y – z = 0} \right\}\]

\[\left\{ {\begin{array}{*{20}{c}}{x + y = 0\;\;\;\;\;\;\;\;\;\;\;\;\;{\pi _1}}\\{x – y – z = 0\;\;\;\;\;\;{\pi _2}}\end{array}\;\;\;\;\;,\;\;\;\;{\pi _1} \cap {\pi _2} = r} \right.\]

La intersección de dos planos no paralelos es una recta. ¿Cómo podemos encontrar una base de una recta?

\[y = – x\;\]

\[\; \Rightarrow \;\;x – \left( { – x} \right) – z = 0\; \Rightarrow \;\;z = 2x\]

Si llamamos \(x = t\) , resulta:

\[\left( {x,y,z} \right) = \left( {t, – t,2t} \right) = t\left( {1, – 1,2} \right)\]

Observamos que todos los vectores de la recta pueden expresarse como combinación lineal del vector director \(\left( {1, – 1,2} \right)\), que además es LI Por lo tanto, \(\left\{ {\;\left( {1, – 1,2} \right)\;} \right\}\) es una base de este subespacio.

Las rectas que pasan por el origen son subespacios de dimensión 1.

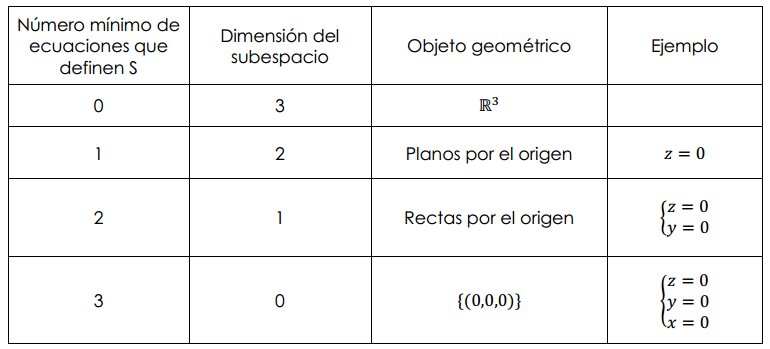
En los ejemplos anteriores observamos cómo disminuye la dimensión de un subespacio a medida que agregamos ecuaciones, tal como se muestra en el siguiente cuadro:

\[V = {\mathbb{R}^3}\]

Ejercicio para el lector 1

Indicar si \(A = \left\{ {\left( {1,1,1} \right),\;\left( {1,3,2} \right)} \right\}\) es una base de \(W = \left\{ {\left( {x,y,z,} \right) \in {R^3}:\;\;x + y – 2z = 0\;\;} \right\}\;\), justificando la respuesta.

Ejemplo 1

Consideremos el siguiente subespacio de R⁴ y busquemos base y dimensión:

\[{T_1} = \left\{ {\left( {{x_1},{x_2},{x_3},{x_4}} \right) \in {R^4}|\;{x_1} + {x_4} = 0\; \wedge \;{x_2} – {x_4} = 0} \right\}\]

Teniendo en cuenta las ecuaciones que definen \({T_1}\), ¿podrían anticipar su dimensión?

Observación: Como \({x_3}\) no aparece en las ecuaciones que definen el subespacio, un error frecuente es suponer \({x_3} = 0\) .

Si \({x_3}\) no está en las ecuaciones, significa que es una variable libre, o sea que puede tomar cualquier valor real.

Entonces:

\[{T_1}:\;\;\left\{ {\begin{array}{*{20}{c}}{{x_1} = – {x_4}}\\{{x_2} = {x_4}}\end{array}\;\;\;} \right.\;\forall {x_{3\;\;,\;\;\;}}\forall {x_4}\;\;\;\;\]

Escribimos el vector genérico (representativo) del subespacio que debe quedar expresado en función de las variables libres \({x_3}\) y \({x_4}\) :

\[\left( { – {x_4},{x_4},{x_3},{x_4}} \right) = {x_3}\left( {0,0,1,0} \right) + {x_4}\left( { – 1,1,0,1} \right)\]

Encontramos dos vectores L.I. que generan el subespacio. Entonces una base de \({T_1}\) es:

\({B_{{T_1}}} = \left\{ {\left( {0,0,1,0} \right),\left( { – 1,1,0,1} \right)} \right\}\;\;{\rm{\;\;por\;lo\;tanto\;\;}}\;\dim \left( {{T_1}} \right) = 2\)

Ejemplo 2

Hallemos una base y la dimensión del subespacio de matrices simétricas de 2×2:

\[{T_2} = \left\{ {A \in {R^{2 \times 2}}\;|\;\;A = {A^t}} \right\}\]

¿Cómo es una matriz simétrica de 2×2? \(\;\;A = \left( {\begin{array}{*{20}{c}}a&b\\b&c\end{array}} \right)\)

\[\left( {\begin{array}{*{20}{c}}a&b\\b&c\end{array}} \right) = a\left( {\begin{array}{*{20}{c}}1&0\\0&0\end{array}} \right) + b\left( {\begin{array}{*{20}{c}}0&1\\1&0\end{array}} \right) + c\left( {\begin{array}{*{20}{c}}0&0\\0&1\end{array}} \right)\]

Las tres matrices halladas son L.I. y generan el subespacio de matrices simétricas, por lo tanto hemos encontrado una base de dicho subespacio:

Ejercicio para el lector 2

Hallar una base y la dimensión del subespacio de matrices antisimétricas de 2×2 y de 3×3.

Ejemplo 3

Hallar base y dimensión de \(S = \left\{ {p\left( x \right) \in {P_2}|\;{a_0} – 2{a_1} + 3{a_2} = 0} \right\}\)

Resolución

¿Cómo es un polinomio de \({P_2}\)?

\[p\left( x \right) = {a_0} + {a_1}x + {a_2}{x^2}\]

La dimensión de P₂ es 3, pero estamos agregando la condición \({a_0} – 2{a_1} + 3{a_2} = 0\).

Podemos anticipar que la dimensión del subespacio es 2, para comprobarlo busquemos una base:

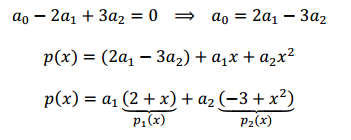
Estos dos vectores generan \(S\), y además vemos que son LI.

Entonces encontramos una base del subespacio:

\[{B_S} = \left\{ {2 + x\;,\; – 3 + {x^2}} \right\}\]

\[\dim \left( S \right) = 2\]

Bases de subespacios definidos por generadores

Hasta ahora hemos buscado bases de subespacios definidos por ecuaciones. ¿Qué ocurre cuando el subespacio está definido por sus generadores?

Veamos el siguiente ejemplo:

Hallar una base y la dimensión de \(S = gen\left\{ {\left( {1,1,2} \right),\left( {1, – 1,0} \right),\;\left( {0,1,1} \right)} \right\} \subset {R^3}\).

En este caso, por la definición de S sabemos que \(\left\{ {\left( {1,1,2} \right),\left( {1, – 1,0} \right),\;\left( {0,1,1} \right)} \right\}\) es un conjunto generador de S. Para determinar si es una base, tendremos que analizar la independencia lineal:

– Si son vectores LI, entonces son base del subespacio.

– Si son LD, tendremos que extraer una base eliminando los vectores «que sobren».

En el caso específico de 3 vectores en R³, podemos utilizar el determinante (que es el producto mixto). Como en este caso el determinante da cero, los vectores son coplanares y por lo tanto L.D. Tenemos que extraer una base eliminando alguno de los vectores, por ejemplo:

• \(\left\{ {\left( {1,1,2} \right),\left( {1, – 1,0} \right)} \right\}\) es una base de S
• \(\left\{ {\left( {1, – 1,0} \right),\;\left( {0,1,1} \right)} \right\}\) es otra base de S.

Podemos afirmar que la dimensión de S es 2.

Una forma práctica de extraer bases es armar una matriz con los vectores dados y llevarla a la forma escalonada:

Una matriz cualquiera puede llevarse a la forma escalonada aplicando operaciones elementales entre sus filas. Por ejemplo consideremos la matriz que armamos con los generadores de \(S\):

\[\left( {\begin{array}{*{20}{c}}1&1&2\\1&{ – 1}&0\\0&1&1\end{array}} \right)\;\mathop \to \limits_{{F_2} \to {F_1} – {F_2}} \;\;\;\left( {\begin{array}{*{20}{c}}1&1&2\\0&2&2\\0&1&1\end{array}} \right)\;\;\;\mathop \to \limits_{{F_3} \to {F_2} – 2{F_3}} \;\;\;\left( {\begin{array}{*{20}{c}}1&1&2\\0&2&2\\0&0&0\end{array}} \right)\]

Se denomina rango de una matriz al número de filas LI que tiene la matriz. Veremos en la siguiente unidad la importancia de este concepto en el estudio de sistemas de ecuaciones lineales.

Puede demostrarse que:

1. Si se realizan operaciones elementales entre las filas de una matriz, el rango se conserva.

2. Las filas no nulas de una matriz escalonada son LI.

Por lo tanto, para determinar el rango de una matriz se aplican operaciones elementales para obtener una matriz escalonada y se cuentan las filas no nulas.

En el ejemplo, la matriz escalonada tiene rango 2, por lo tanto la matriz que armamos con los generadores de S tiene rango 2. Esto significa que de los tres generadores de S hay dos linealmente independientes. ¿Cuál es entonces la dimensión de S? \(\dim \left( S \right) = 2\;\)

Este método también permite obtener bases: las filas no nulas de la última matriz son otra base de S, ya que fueron obtenidas como combinaciones lineales de los vectores de S:

\[\left\{ {\left( {1,1,2} \right),\;\left( {0,2,2} \right)} \right\}\;otra\;base\;de\;S\]

Ejemplo

Dado el conjunto:

\[A = \left\{ {1 + x;1 – {x^2};2 + 3x + k{x^2}} \right\} \subset {P_2}\]

Hallar todos los valores de \(k\) par que \(A\) genere un subespacio de dimensión 2

Para el \(k\) hallado encontrar las ecuaciones del subespacio generado por \(A\).

Resolución

Sabemos que \(\dim \left( {{P_2}} \right) = 3\) , entonces todo conjunto de 3 vectores LI en \({P_2}\) es base de \({P_2}\). Como se pide que la dimensión del subespacio sea 2, debemos hallar \(k\) de modo que los vectores sean LD.

Los dos primeros vectores de \(A\) son LI, entonces se trata de analizar para qué valores de \(k\) el tercer vector es combinación lineal de los anteriores:

\[2 + 3x + k{x^2} = \alpha \left( {1 + x} \right) + \beta \left( {1 – {x^2}} \right)\]

\[\left\{ {\begin{array}{*{20}{c}}{2 = \alpha + \beta }\\{3 = \alpha }\\{k = – \beta }\end{array}} \right.\; \Rightarrow \alpha = 3\;,\;\beta = – 1,\;\;k = 1\]

Para \(k = 1\), el polinomio \(2 + 3x + k{x^2}\) es combinación lineal de \(1 + x\) y \(1 – {x^2}\). Entonces:

\[gen\left\{ {1 + x;1 – {x^2};2 + 3x + {x^2}} \right\} = gen\left\{ {1 + x;1 – {x^2}} \right\}\]

\[\left\{ {1 + x;1 – {x^2}} \right\}\;es\;base\;de\;{P_2}\]

Ahora busquemos la ecuación del subespacio. Tomamos un polinomio genérico, \(p\left( x \right) = {a_0} + {a_1}x + {a_2}{x^2}\) y lo escribimos como combinación lineal de los vectores de la base:

\[{a_0} + {a_1}x + {a_2}{x^2} = \alpha \left( {1 + x} \right) + \beta \left( {1 – {x^2}} \right)\]

\[\left\{ {\begin{array}{*{20}{c}}{\alpha + \beta = {a_0}}\\{ – \beta = {a_2}}\\{\alpha = {a_1}}\end{array}\; \Rightarrow \;\alpha = {a_1}\; \wedge \;\;\beta = – {a_2}\;\; \Rightarrow \;{a_0} = {a_1} – {a_2}} \right.\]

Entonces ésa es la ecuación que define al subespacio:

\[S = gen\left( A \right) = \left\{ {p \in {P_2}\;\;|\;\;{a_0} – {a_1} + {a_2} = 0} \right\}\]

Como verificación, puede comprobarse que los dos vectores de la base verifican la ecuación obtenida.

Videos con ejercicios resueltos sobre espacios vectoriales