Intersección
Sean \(S\) y \(T\) subespacios del mismo espacio vectorial \(V\). Definimos la intersección como sigue:
\(S \cap T = \left\{ {v \in V\;:\;v \in S\;\; \wedge \;\;v \in T} \right\}\;\) intersección de subespacios
Propiedad
\(S \cap T\) es subespacio de \(V\)
Demostración
1. \({0_V} \in S \wedge {0_V} \in T \Rightarrow {0_V} \in S \cap T\)
2. Consideremos \(u,\;v\; \in \;S \cap T\;\;\;\;\)
\[ \Rightarrow \;\;\;u \in S\;\;\; \wedge \;\;\;u \in T\;\;\;\; \wedge \;\;\;v \in S\;\;\;\; \wedge \;\;\;\;v \in T\]
\[u \in S\;\;\; \wedge \;\;\;\;v \in S\;\; \Rightarrow \;\;\;\;\;u + v \in S\;\;\;\left[ 1 \right]\]
\[u \in T\;\;\; \wedge \;\;\;\;v \in T\;\; \Rightarrow \;\;\;\;\;u + v \in T\;\;\;\left[ 2 \right]\]
De [1] y [2] se deduce que \(u + \;v\; \in \;S \cap T\;\;\;\;\)
3. Dejamos a cargo del lector demostrar:
\[u \in S \cap T \Rightarrow \left( {ku} \right) \in S \cap T\]
Ejemplo 1
Sean los subespacios de \({\mathbb{R}^3}\):
\[S = \left\{ {\left( {x,y,z} \right)|\;x – 3z = 0} \right\}\]
\[T = \left\{ {\left( {x,y,z} \right)|\;x + y – z = 0} \right\}\]
Hallar \(S \cap T\).
Resolución
Por definición \(S \cap T\) es un conjunto que estará formado por los vectores que pertenezcan a \(S\) y a \(T\). Es decir aquellos vectores que satisfagan las ecuaciones de \(S\) y las de \(T\):
\[S \cap T = \left\{ {\left( {x,y,z} \right)|\;x – 3z = 0\;\; \wedge \;\;\;x + y – z = 0} \right\}\]
Se trata de una recta definida como intersección de dos planos. Una base de la recta es un vector director.
Geométricamente podemos buscar el vector director como el producto vectorial de los vectores normales a los planos:
\[v = {n_1} \times {n_2} = \left| {\begin{array}{*{20}{c}}i&j&k\\1&0&{ – 3}\\1&1&{ – 1}\end{array}} \right| = \left( {3, – 2,1} \right)\]
\[S \cap T = \left\{ {\left( {x,y,z} \right) = \lambda \left( {3, – 2,1} \right)\;\;,\;\;\;\lambda \in \mathbb{R}} \right\}\]
Entonces \(\left\{ {\;\left( {3, – 2,1} \right)\;} \right\}\) es una base de \(S \cap T\).
Otra forma de resolverlo es buscar la solución del sistema de ecuaciones:
\[\;\left\{ {\begin{array}{*{20}{c}}{x – 3z = 0}\\{x + y – z = 0}\end{array}\; \Rightarrow \;} \right.\left\{ {\begin{array}{*{20}{c}}{x = 3z}\\{y = z – x = – 2z}\end{array}\; \Rightarrow \;\left( {3z, – 2z,z} \right)\forall z \in \mathbb{R}\;} \right.\]
\[\left( {x,y,z} \right) = z\left( {3, – 2,1} \right)\]
Y entonces otra vez llegamos a que \(\left\{ {\;\left( {3, – 2,1} \right)\;} \right\}\) es una base de \(S \cap T\).
Ejemplo 2
Sean los subespacios de \({\mathbb{R}^{2 \times 2}}\):
\[S = \left\{ {A \in {\mathbb{R}^{2 \times 2}}\;|\;\;A = {A^t}} \right\}\]
\[T = gen\;\left\{ {\left( {\begin{array}{*{20}{c}}1&0\\2&{ – 1}\end{array}} \right),\left( {\begin{array}{*{20}{c}}1&0\\1&0\end{array}} \right)} \right\}\]
Hallar \(S \cap T\).
Resolución
La intersección de subespacios está formada por los vectores que verifican las ecuaciones de dichos subespacios.
¿Qué tiene que cumplir una matriz para pertenecer a \(S\)?
\[S = \left\{ {\left( {\begin{array}{*{20}{c}}a&b\\c&d\end{array}} \right) \in {\mathbb{R}^{2 \times 2}}\;\;|\;\;\;\;c = b} \right\}\]
¿Qué tiene que cumplir una matriz para pertenecer a \(T\)?
Tiene que poder escribirse como combinación lineal de: \(\left( {\begin{array}{*{20}{c}}1&0\\2&{ – 1}\end{array}} \right)\;y\left( {\begin{array}{*{20}{c}}1&0\\1&0\end{array}} \right)\)
Hallemos las ecuaciones del subespacio \(T\):
\[\left( {\begin{array}{*{20}{c}}a&b\\c&d\end{array}} \right) = \alpha \left( {\begin{array}{*{20}{c}}1&0\\2&{ – 1}\end{array}} \right) + \beta \left( {\begin{array}{*{20}{c}}1&0\\1&0\end{array}} \right)\]
\[\left( {\begin{array}{*{20}{c}}a&b\\c&d\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{\alpha + \beta }&0\\{2\alpha + \beta }&{ – \alpha }\end{array}} \right)\]
\[\left\{ {\begin{array}{*{20}{c}}{a = \alpha + \beta }\\{b = 0\;}\\{c = 2\alpha + \beta \;}\\{d = – \alpha \;\;\;}\end{array}} \right.\;\; \Rightarrow \;\;\;\;\left\{ {\begin{array}{*{20}{c}}{\beta = a + d}\\{b = 0}\\{\beta = c + 2d}\\{\alpha = – d}\end{array}} \right.\;\;\;\; \Rightarrow \;\;\left\{ {\begin{array}{*{20}{c}}{a + d = c + 2d}\\{b = 0}\end{array}} \right.\]
\[ \Rightarrow \;\;\;T = \left\{ {\left( {\begin{array}{*{20}{c}}a&b\\c&d\end{array}} \right)|\;\;b = 0\; \wedge \;\;a – c – d = 0} \right\}\]
Ahora planteamos que las matrices de \(S \cap T\;\) deben cumplir con las ecuaciones de \(S\) y las de \(T\):
\[S \cap T = \left\{ {\left( {\begin{array}{*{20}{c}}a&b\\c&d\end{array}} \right) \in \mathbb{R}\;\;|\;\;\;b = c\; \wedge \;b = 0\; \wedge \;a – c – d = 0} \right\}\]
O sea:
\[b = c = 0\;\; \wedge \;\;a = d\]
Entonces las matrices de \(S \cap T\) son de la forma:
\[\left( {\begin{array}{*{20}{c}}a&0\\0&a\end{array}} \right) = a\left( {\begin{array}{*{20}{c}}1&0\\0&1\end{array}} \right)\]
Y una base de \(S \cap T\) es:
\[{B_{S \cap T}} = \left\{ {\left( {\begin{array}{*{20}{c}}1&0\\0&1\end{array}} \right)} \right\}\]
Hay un método alternativo más breve para hallar una base de \(S \cap T\) sin necesidad de obtener las ecuaciones de \(T\), como veremos a continuación.
Escribamos una matriz de \(T\) como combinación lineal de los vectores que la generan:
Pero además deben cumplirse las ecuaciones de \(S\) que establecen que \(c = b\). Entonces:
\[2\alpha + \beta = 0 \Rightarrow \;\beta = – 2\alpha \; \Rightarrow \;\left\{ {\begin{array}{*{20}{c}}{a = – \alpha }\\{b = 0}\\{c = 0}\\{d = – \alpha }\end{array}} \right.\]
Por lo tanto, una matriz de \(S \cap T\) es:
\[\left( {\begin{array}{*{20}{c}}{ – \alpha }&0\\0&{ – \alpha }\end{array}} \right) = – \alpha \left( {\begin{array}{*{20}{c}}1&0\\0&1\end{array}} \right)\; \Rightarrow \;\;\;\;{B_{S \cap T}} = \left\{ {\left( {\begin{array}{*{20}{c}}1&0\\0&1\end{array}} \right)} \right\}\]
Suma de subespacios
Dados \(S,\;T\;\) subespacios de \(V\), se define la suma como sigue:
\(S + T = \left\{ {v \in V\;:\;\;v = {v_1} + {v_2}\;\;,\;\;\;con\;\;{v_1} \in S\;,\;\;{v_2} \in T} \right\}\) suma de subespacios
Propiedad: \(S + T\) es un subespacio del espacio vectorial \(V\).
Dejamos la demostración a cargo del lector.
Si conocemos conjuntos generadores de S y de T, podemos hallar generadores de la suma:
\(S = gen\left\{ {{v_1},{v_2}, \ldots ,{v_q}} \right\}\) y \(T = gen\left\{ {{w_1},{w_2}, \ldots ,{w_r}} \right\}\) \(\; \Rightarrow \;S + T = gen\left\{ {{v_1},{v_2}, \ldots {v_q},{w_1},{w_2}, \ldots ,{w_r}} \right\}\)
Para hallar la suma es usual buscar las bases de \(S\) y \(T\). Como las bases son conjuntos generadores LI, si conocemos una base de cada subespacio podremos obtener un conjunto generador de la suma:
Dadas las bases:
\({B_s} = \left\{ {{v_1},{v_2}, \ldots ,{v_q}} \right\}\) y \({B_T} = \left\{ {{w_1},{w_2}, \ldots ,{w_r}} \right\}\)
Resulta:
\(\left\{ {{v_1}, \ldots ,{v_q},{w_1}, \ldots ,{w_r}} \right\}\) conjunto generador de la suma.
Observación: Se obtiene así un conjunto generador de la suma pero no siempre es linealmente independiente.
- Si es LI, encontramos una base de la suma.
- Si es LD, podemos extraer una base de la suma eliminando los vectores «que sobran».
Ejemplo 1
Dados los siguientes subespacios de \(V = {\mathbb{R}^3}\):
\[S = \left\{ {\left( {x,y,z} \right)|\;x – 3z = 0} \right\}\]
\[T = \left\{ {\left( {x,y,z} \right)|\;x + y – z = 0} \right\}\]
Nos interesa hallar \(S + T\).
Busquemos una base de \(S\). Para eso en la ecuación despejamos una variable:
\[x = 3z\]
Ahora armamos un vector genérico:
\[\left( {x,y,z} \right) = \left( {3z,y,z} \right) = z\left( {3,0,1} \right) + y\left( {0,1,0} \right)\]
\[{B_S} = \left\{ {\left( {3,0,1} \right),\left( {0,1,0} \right)} \right\}\]
Busquemos una base de \(T\). Para esto en la ecuación despejamos una variable:
\[z = x + y\]
Ahora armamos un vector genérico:
\[\left( {x,y,z} \right) = \left( {x,y,x + y} \right) = x\left( {1,0,1} \right) + y\left( {0,1,1} \right)\]
Entonces
\[{B_T} = \left\{ {\left( {1,0,1} \right),\left( {0,1,1} \right)} \right\}\]
\[S + T = gen\left\{ {\left( {3,0,1} \right),\left( {0,1,0} \right),\left( {1,0,1} \right),\left( {0,1,1} \right)} \right\}\]
Sabemos que todo conjunto de más de 3 vectores en \({\mathbb{R}^3}\) es linealmente dependiente, ya que la dimensión de \({\mathbb{R}^3}\) es 3. ¿Cómo podemos extraer una base de la suma?
Podríamos armar una matriz con estos 4 vectores y llevarla a la forma escalonada. O si no, como el espacio es \({\mathbb{R}^3}\) podemos pensar geométricamente:
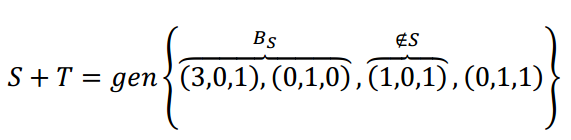
Como \(\left( {1,0,1} \right)\) no verifica la ecuación del plano S, los 3 primeros vectores no son coplanares y por lo tanto forman una base de \(\mathbb{R}^3\). Podemos eliminar \(\left( {0,1,1} \right)\) porque es combinación lineal de dicha base.
Por lo tanto: \(B = \left\{ {\left( {3,0,1} \right),\left( {0,1,0} \right),\left( {1,0,1} \right)} \right\}\) es base de \(S + T\) y es base de \(\mathbb{R}^3\).
En este caso, como \(S + T\;\) es un subespacio de \({R^3}\) de dimensión 3, podemos afirmar que:
\[S + T = {\mathbb{R}^3}\]
Generalizando:
\(S\) subespacio de \(V\) y \(\dim \left( S \right) = \dim \left( V \right) \Rightarrow S = V\)
Ejemplo 2
Dados los siguientes subespacios de \(V = {\mathbb{R}^4}\):
\[{S_1} = \left\{ {x \in {\mathbb{R}^4}|\;{x_1} + {x_2} = {x_2} + {x_4} = 0} \right\}\]
\[{S_2} = \left\{ {x \in {\mathbb{R}^4}|\;{x_1} – {x_4} = {x_3} + {x_4} = 0} \right\}\]
Hallar base y dimensión de \({S_1} + {S_2}\;\).
Resolución
\[\left( {{x_1},{x_2},{x_3},{x_4}} \right) = \left( { – {x_2},{x_2},{x_3}, – {x_2}} \right) = {x_2}\left( { – 1,1,0, – 1} \right) + {x_3}\left( {0,0,1,0} \right)\]
\[{B_{{S_1}}} = \left\{ {\left( {1, – 1,0,1} \right),\left( {0,0,1,0} \right)} \right\}\]
\[\left( {{x_1},{x_2},{x_3},{x_4}} \right) = \left( {{x_4},{x_2}, – {x_4},{x_4}} \right) = {x_4}\left( {1,0, – 1,1} \right) + {x_2}\left( {0,1,0,0} \right)\]
\[{B_{{S_2}}} = \left\{ {\left( {1,0, – 1,1} \right),\left( {0,1,0,0} \right)} \right\}\]
\[{S_1} + {S_2} = gen\left\{ {\left( {1, – 1,0,1} \right),\left( {0,0,1,0} \right),\left( {1,0, – 1,1} \right),\left( {0,1,0,0} \right)} \right\}\]
Cómo hemos visto, un método para analizar si son LI o LD, consiste en armar una matriz con los vectores como filas y llevarla a su forma escalonada. Por conveniencia colocaremos los vectores en el siguiente orden:
\(\left( {\begin{array}{*{20}{c}}1&{ – 1}&0&1\\1&0&{ – 1}&1\\0&1&0&0\\0&0&1&0\end{array}} \right)\)
\(\mathop \to \limits_{{F_2} \to {F_2} – {F_1}} \left( {\begin{array}{*{20}{c}}1&{ – 1}&0&1\\0&1&{ – 1}&0\\0&1&0&0\\0&0&1&0\end{array}} \right)\)
\(\mathop \to \limits_{{F_3} \to {F_3} – {F_2}} \left( {\begin{array}{*{20}{c}}1&{ – 1}&0&1\\0&1&{ – 1}&0\\0&0&1&0\\0&0&1&0\end{array}} \right)\)
\(\mathop \to \limits_{{F_4} \to {F_4} – {F_3}} \left( {\begin{array}{*{20}{c}}1&{ – 1}&0&1\\0&1&{ – 1}&0\\0&0&1&0\\0&0&0&0\end{array}} \right)\)
La matriz escalonada tiene 3 filas LI (su rango es 3), entonces podemos afirmar que la dimensión de \(S + T\) es 3.
Como se anuló la última fila, el vector \(\left( {0,0,1,0} \right)\) es combinación lineal de los otros tres, por lo tanto una base de \(S + T\) es: \({B_{S + T}} = \left\{ {\left( {1, – 1,0,1} \right),\left( {0,1,0,0} \right),\left( {1,0, – 1,1} \right)} \right\}\).
Recordemos que las filas de la matriz escalonada componen otra base de la suma:
\[B{‘_{S + T}} = \left\{ {\left( {1, – 1,0,1} \right),\left( {0,1, – 1,0} \right),\left( {0,0,1,0} \right)} \right\}\]
Suma directa
La suma de dos subespacios es directa si y sólo si la intersección de los subespacios es el vector nulo.
\[S + T\;es\;directa\; \Leftrightarrow \;S \cap T = \left\{ {{0_V}} \right\}\]
Cuando la suma es directa se escribe:
\[S \oplus T\]
Ejemplos en \({\rm{V}} = {\mathbb{R}^3}\)
A continuación consideraremos diferentes casos de suma de subespacios en \({\mathbb{R}^3}\).
Dos rectas
Un caso posible de suma de dos subespacios en \({\mathbb{R}^3}\) es el de dos rectas que se cortan:
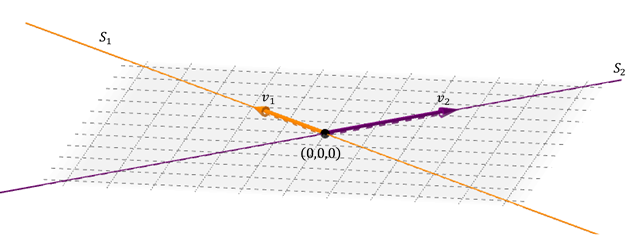
Los dos vectores LI de las rectas generan un plano: aquél que contiene a ambas rectas. La suma es directa porque la intersección entre las rectas es el vector nulo.
\[{S_1} \cap {S_2} = \left\{ {\left( {0,0,0} \right)} \right\}\;\;\;y\;\;\;{S_1} + {S_2} = gen\left\{ {{v_1},{v_2}} \right\}\;\]
\({S_1} \oplus {S_2} = S\) donde \(S\) es el plano que contiene a las dos rectas
Dos planos que se cortan
Otro caso posible de suma de dos subespacios en \({\mathbb{R}^3}\) es el de dos planos que se cortan en una recta:
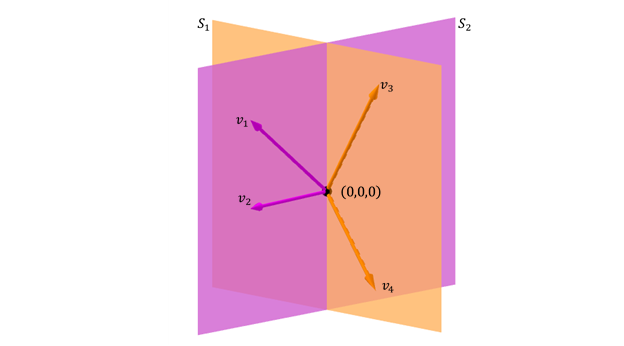
\[{S_1} \cap {S_2} \ne \left\{ {{0_V}} \right\}\;\;\;y\;\;\;{S_1} + {S_2} = gen{\rm{\{ }}{v_1},{v_2},{v_3},{v_4}{\rm{]}} = gen\left\{ {\;{v_1},{v_2},{v_3}} \right\}\]
La suma de los subespacios es \({\mathbb{R}^3}\) pero no es suma directa porque la intersección no es el vector nulo:
\[{S_1} + {S_2} = {\mathbb{R}^3}\;\]
Un plano y una recta incluida en el plano
Otro caso posible de suma de dos subespacios en \({\mathbb{R}^3}\) es el de un plano y una recta incluida en el plano. 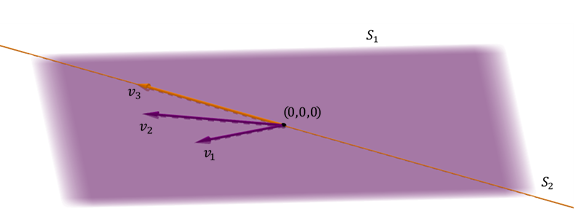
\[{S_1} + {S_2} = {S_1}\;\;\;\;\;\;\;pues\;\;\;{S_2} \subset {S_1}\]
Se obtiene el mismo plano, y la suma no es directa porque la intersección no es igual al vector nulo.
Un plano y una recta no incluida en el plano
Otro caso posible de suma de dos subespacios en \({\mathbb{R}^3}\) es el de un plano y una recta no incluida en el plano. 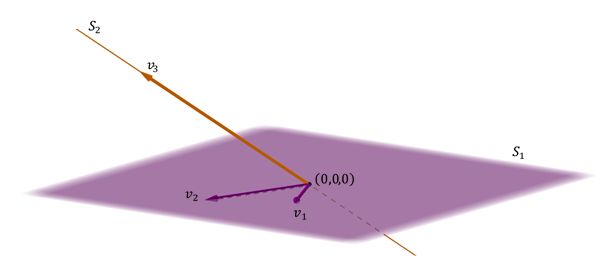
\[{S_1} \cap {S_2} = \left\{ {\left( {0,0,0} \right)} \right\}\;\;\;\;\;y\;\;\;\;\;{S_1} + {S_2} = gen\left\{ {{v_1},{v_{2,}}{v_3}} \right\} = {\mathbb{R}^3}\;\;\]
Se genera \({\mathbb{R}^3}\) porque el vector director de la recta no es coplanar con los vectores del plano, y además es directa porque la intersección es el vector nulo:
\[{S_1} \oplus {S_2} = {\mathbb{R}^3}\]
Observación: En el último caso, la unión de las bases de los dos subespacios forma una base de todo el espacio. En este caso, cada vector de \({\mathbb{R}^3}\) puede expresarse de forma única como suma de un vector de \({S_1}\) y otro de \({S_2}\).
Ejercicio para el lector 3
Dados \({S_1} = gen\left\{ {\left( {1,2,1} \right),\;\left( {0,2,0} \right)} \right\}\) y \({S_2} = \left\{ {\left( {x,y,z} \right):\;\;\;x + y = y – kz = 0} \right\}\),
a) Hallar los valores de \(k\) para los cuales \({S_1} \oplus {S_1} = {\mathbb{R}^3}\).
b) Para \(k = 0\) , comprobar que \(v = \left( {3,2,1} \right)\) puede expresarse de forma única como suma de un vector \({v_1} \in {S_1}\) y otro de \({v_2} \in {S_2}\).
Ejercicio para el lector 4
Sean los subespacios de \({\mathbb{R}^4}\):
\(S = gen\left\{ {\left( {1,1,1,1} \right),\;\left( {0,1,0,1} \right)} \right\}\) y \(T = \left\{ {\left( {x,y,z,t} \right):\;\;\;x – z = 0\;\;\;,\;\;x – z + t = 0} \right\}\)
¿Cuál de las siguientes afirmaciones es correcta? Justificar.
- \(S \oplus T = {\mathbb{R}^4}\)
- \(S + T = {\mathbb{R}^4}\)
- \(S + T = W\;\;\;y\;\dim \left( W \right) = 3\)
- \(S \oplus T = W\) y \(\dim \left( W \right) = 3\)
Teorema de la dimensión de la suma
Si \({S_1}\) y \({S_2}\) son subespacios de un espacio vectorial \(V\) (de dimensión finita), entonces:
\[\dim \left( {{S_1} + {S_2}} \right) = \dim \left( {{S_1}} \right) + \dim \left( {{S_2}} \right) – dim\left( {{S_1} \cap {S_2}} \right)\]
En el caso particular de que la suma sea directa, como \({S_1} \cap {S_2} = \left\{ {{0_V}} \right\}\) , resulta:
\[\dim \left( {{S_1} \oplus {S_2}} \right) = \dim \left( {{S_1}} \right) + \dim \left( {{S_2}} \right)\]
Ejemplo
Dados los subespacios de \({P_2}\):
\[{S_1} = \left\{ {p \in {P_2}\;|\;\;p\left( 0 \right) = 0} \right\}\]
\[{S_2} = \left\{ {p \in {P_2}\;|\;\;p\left( 1 \right) = 0} \right\}\]
Hallar bases de ambos subespacios y de la intersección
Resolución
Hallemos una base de \({S_1}\):
\[p\left( 0 \right) = {a_0} + {a_1}0 + {a_2}{0^2} = 0 \Rightarrow {a_0} = 0\]
Entonces son los polinomios de la forma:
\[{a_1}x + {a_2}{x^2}\]
Luego una base de \({S_1}\) es:
\[{B_{{S_1}}} = \left\{ {x,{x^2}} \right\} \Rightarrow \dim \left( {{S_1}} \right) = 2\]
Hallemos una base de \({S_2}\):
\[p\left( 1 \right) = {a_0} + {a_1}1 + {a_2}{1^2} = 0 \Rightarrow {a_0} + {a_1} + {a_2} = 0\]
Entonces son los polinomios de la forma:
\[\left( { – {a_1} – {a_2}} \right) + {a_1}x + {a_2}{x^2} = {a_1}\left( { – 1 + x} \right) + {a_2}\left( { – 1 + {x^2}} \right)\]
\[{B_{{S_2}}} = \left\{ { – 1 + x\;\;,\;\;\; – 1 + {x^2}} \right\}\; \Rightarrow \;\dim \left( {{S_2}} \right) = 2\]
Para buscar \({S_1} \cap {S_2}\) debemos plantear que se cumplan las ecuaciones de \({S_1}\) y también las de \({S_2}\):
\[{a_0} = 0\; \wedge \;\;{a_0} + {a_1} + {a_2} = 0 \Rightarrow \;\;{a_0} = 0\;\; \wedge \;\;{a_1} = – {a_2}\]
Los polinomios serán de la forma:
\[{a_1}x – {a_1}{x^2} = {a_1}\left( {{x^2} – x} \right)\]
Luego:
\[{B_{{S_1} \cap {S_2}}} = \left\{ {{x^2} – x} \right\}\; \Rightarrow \;\dim \left( {{S_1} \cap {S_2}} \right) = 1\]
Nótese que como conocemos las dimensiones de \({S_1}\), \({S_2}\) y \({S_1} \cap {S_2}\), podemos calcular la dimensión de \({S_1} + {S_2}\):
\[\dim \left( {{S_1} + {S_2}} \right) = 2 + 2 – 1 = 3\]
Pero el único subespacio de \({P_2}\) con dimensión 3 es \({P_2}\). Luego: \({S_1} + {S_2} = {P_2}\).
Ejercicio para el lector 5
Dados los subespacios de \({\mathbb{R}^{2 \times 2}}\):
\[{W_1}:\left\{ {A \in {\mathbb{R}^{2 \times 2}}\;\;|\;\;A = {A^t}} \right\}\]
\[{W_2}:\left\{ {A \in {\mathbb{R}^{2 \times 2}}\;|\;\;A = – {A^t}} \right\}\]
a) Hallar bases de \({W_1}\) y \({W_2}\)
b) Obtener \({W_1} \cap {W_2}\).
c) Sin hallar \({W_1} + {W_2}\) analizar la validez de la siguiente afirmación:
\[{W_1} \oplus {W_2} = {\mathbb{R}^{2 \times 2}}\]
d) Proponer una base de \({\mathbb{R}^{2 \times 2}}\) formada por matrices simétricas y antisimétricas, y expresar la matriz
\[\left( {\begin{array}{*{20}{c}}1&2\\3&4\end{array}} \right)\]
como suma de una matriz simétrica más una antisimétrica.
Producto interno
En la primera unidad vimos producto escalar entre vectores y sus aplicaciones a la Geometría. En esta sección nos proponemos generalizar esta operación a otros espacios vectoriales definiendo la noción general de producto interno a partir de las propiedades del producto escalar.
Definición: Un producto interno en un espacio vectorial real \(V\) es una operación que asigna a cada par de vectores \(u\) y \(v\) de \(V\) un número real \(u\;.v\) tal que se verifican las siguientes propiedades (para todo vector \(u,\;v,\;w\) de \(V\) y todo escalar \(\alpha \)):1. \(u \cdot v = v \cdot u\)
2. \(u \cdot \left( {v + w} \right) = \left( {u \cdot v} \right) + \left( {u \cdot w} \right)\)
3. \(\alpha u \cdot v = \alpha \left( {u \cdot v} \right)\)
4. \(u.u \ge 0\;\;\; \wedge \;\;\;u.u = 0\;\;\;\; \Leftrightarrow \;\;\;\;u = {0_V}\)
Es posible definir así distintos productos internos en cualquier espacio vectorial (mientras se verifiquen estas propiedades). En nuestra materia, sólo trabajaremos con el producto interno canónico en \({\mathbb{R}^n}\), que es la extensión del producto escalar:
\(\left( {{x_1},{x_2}, \ldots ,{x_n}} \right).\left( {{y_1},{y_2}, \ldots ,{y_n}} \right) = {x_1}{y_1} + {x_2}{y_2} + \ldots {x_n}{y_n}\) producto interno canónico en \(\mathbb{R}^n\)
Esta definición nos permite extender el concepto de ortogonalidad a \({\mathbb{R}^n}\):
\(u \bot v\;\;\; \Leftrightarrow \;\;u.v = 0\) condición de ortogonalidad
Ejemplo
Realicemos el producto interno de los vectores de \({\mathbb{R}^4}\):
\[u = \left( {1,2,3,4} \right)\;\;\;\;\;\;\;\;\;v = \left( {1,0,1, – 1} \right)\]
\[u.v = 1.1 + 2.0 + 3.1 + 4.\left( { – 1} \right) = 0\]
Como \(u.v = 0\) entonces \(u\) y \(v\) son ortogonales.\(\;\)
Complemento ortogonal de un subespacio
Sea \(S\) subespacio de \(V\) (espacio vectorial con producto interno).
El complemento ortogonal de \(S\), que denotamos como \({S^ \bot }\) , es el conjunto de vectores de \(V\) que son ortogonales a cada uno de los vectores de \(S\):
\({S^ \bot } = \left\{ {\;v \in V\;:\;\;v \cdot w = 0\;\;\;\;\forall w \in S\;} \right\}\) complemento ortogonal de \(S\)
Propiedad: \({S^ \bot }\) es un subespacio de \(V\).
1. \({0_V}\) pertenece a \({S^ \bot }\) pues \({0_V}.w\; = \;0\) para todo \(w\) de \(S\)
2. Sean \(u,v \in {S^ \bot } \Rightarrow u.w\; = \;0 \wedge v.w\; = \;0\;\;\;\;\forall w \in S \Rightarrow \left( {u + v} \right).w\; = \;u.w\; + \;v.w\; = \;0\)
Por lo tanto \(u + v\) está en \({S^ \bot }\)
3. Si \(u \in {S^ \bot } \Rightarrow ku \in {S^ \bot }\). ¿Por qué?
Ejemplo 1
Sea \(S = \left\{ {\left( {x,y,z} \right) \in {\mathbb{R}^3}\;|\;2x + 3y – z = 0} \right\}\). Hallar \({S^ \bot }\).
Resolución
Tenemos que buscar los vectores de \({\mathbb{R}^3}\) que sean perpendiculares a todos los vectores de ese plano.
Primero buscamos una base de \(S\), por ejemplo:
\[{B_S} = \left\{ {\left( { – 1,1,1} \right),\left( {0,1,3} \right)} \right\}\]
Para hallar el complemento ortogonal, buscamos todos los vectores \(\left( {x,y,z} \right)\) que sean ortogonales a \(\left( { – 1,,1,1} \right)\) y a \(\left( {0,1,3} \right)\).
Se obtiene así un sistema de ecuaciones que define el complemento ortogonal:
\[\left\{ {\begin{array}{*{20}{c}}{\left( {x,y,z} \right).\left( { – 1,1,1} \right) = 0}\\{\left( {x,y,z} \right).\left( {0,1,3} \right) = 0}\end{array}} \right.\; \Rightarrow \;\;\left\{ {\begin{array}{*{20}{c}}{ – x + y + z = 0\;\;\;\; \Rightarrow \; – x – 3z + z = 0\;}\\{y + 3z = 0\;\;\;}\end{array}} \right.\;\;\]
\[\;\;\left\{ {\begin{array}{*{20}{c}}{\;x = – 2z}\\{\;y = – 3z}\end{array}} \right.\;\;\;\;\;\;Ecuaciones\;de\;\;{S^ \bot }\;\]
¿Cuál es una base del subespacio \({S^ \bot }\)?
\[{B_{{S^ \bot }}} = \left\{ {\left( { – 2, – 3,1} \right)} \right\}\]
La base es un vector perpendicular al plano \(S\). Por lo tanto, el complemento ortogonal de un plano que pasa por el origen es la recta perpendicular que pasa por el origen.
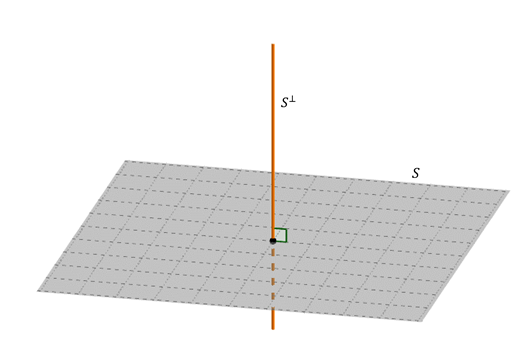
Si \(S\) es una recta que pasa por el origen: ¿cuál es su complemento ortogonal?
Ejercicio para el lector 6
Para justificar el procedimiento que utilizamos para encontrar las ecuaciones de \({S^ \bot }\), les pedimos que demuestren la siguiente propiedad:
Sean \(u,\;v,\;w\) vectores de \({\mathbb{R}^n}\).
Si \(w\) es ortogonal a \(u\) y a \(v\), entonces es ortogonal a cualquier combinación lineal de \(u\) y \(v\).
Ejemplo 2
Dado siguiente subespacio de \({\mathbb{R}^4}\):
\[S = \left\{ {\left( {{x_1},{x_2},{x_3},{x_4}} \right) \in {\mathbb{R}^4}\;\;|\;\;\;{x_1} + {x_2} – 3{x_3} = 0\; \wedge \;{x_2} – {x_4} = 0} \right\}\]
Halle base y dimensión del complemento ortogonal.
Resolución
Tenemos que buscar los vectores de \({\mathbb{R}^4}\) que son ortogonales a los vectores de \(S\).
Hallemos una base de \(S\):
\[\left( { – {x_2} + 3{x_3}\;\;\;,\;\;\;{x_2}\;\;,\;\;\;{x_3}\;\;,\;\;\;{x_2}} \right) = {x_2}\left( { – 1,1,0,1} \right) + {x_3}\left( {3,0,1,0} \right)\]
\[ \Rightarrow {B_S} = \left\{ {\left( { – 1,1,0,1} \right),\left( {3,0,1,0} \right)} \right\}\]
Ahora buscamos los \(\left( {{x_1},{x_2},{x_3},{x_4}} \right)\) tales que:
\[\left\{ {\begin{array}{*{20}{c}}{\left( {{x_1},{x_2},{x_3},{x_4}} \right)\left( {3,0,1,0} \right) = 0}\\{\left( {{x_1},{x_2},{x_3},{x_4}} \right)\left( { – 1,1,0,1} \right) = 0}\end{array}} \right.\;\;\;\; \Rightarrow \;\;\;\;\left\{ {\begin{array}{*{20}{c}}{3{x_1} + {x_3} = 0}\\{ – {x_1} + {x_2} + {x_4} = 0}\end{array}} \right.\]
Hallamos las ecuaciones que definen a \({S^ \bot }\):
\[{S^ \bot } = \left\{ {\left( {{x_1},{x_2},{x_3},{x_4}} \right) \in {\mathbb{R}^4}\;\;|\;\;3{x_1} + {x_3} = 0\; \wedge \; – {x_1} + {x_2} + {x_4} = 0\;\;\;} \right\}\]
Busquemos una base de \({S^ \bot }\):
\[\left( {{x_1}\;\;,\;\;\;{x_2}\;\;,\;\;\; – 3{x_1}\;\;,\;\;\;{x_1} – {x_2}\;\;} \right) = {x_1}\left( {1,0, – 3,1} \right) + {x_2}\left( {0,1,0, – 1} \right)\]
\[ \Rightarrow {B_{{S^ \bot }}} = \left\{ {\left( {1,0, – 3,1} \right),\left( {0,1,0, – 1} \right)} \right\}\;\; \Rightarrow \;\;\dim \left( {{S^ \bot }} \right) = 2\]
Propiedades del complemento ortogonal
Sea \(V\) un espacio vectorial de dimensión finita, con producto interno, y sea \(S\) un subespacio de \(V\). Entonces se verifican las siguientes propiedades:
- \({\left( {{S^ \bot }} \right)^ \bot } = S\)
- \({V^ \bot } = \left\{ {\;{0_V}\;} \right\}\) y \(\left\{ {\;{0_{V\;}}} \right\}{\;^ \bot } = V\)
- \(S \cap {S^ \bot } = \left\{ {{0_V}} \right\}\)
- \(S + {S^ \bot } = V\)
Esta última propiedad significa que cualquier vector de \(V\) puede expresarse como suma de un vector de S más otro de \({S^ \bot }\).
Ilustramos con un ejemplo geométrico de \({\mathbb{R}^3}\):
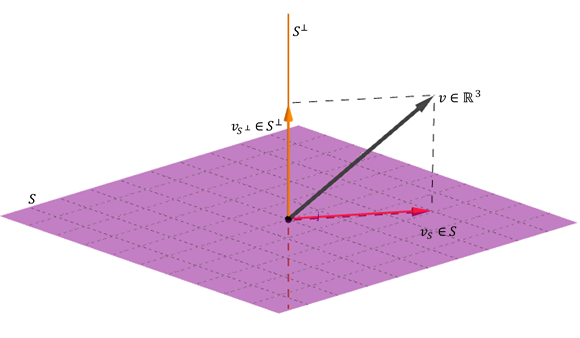
De las propiedades 3 y 4 se deduce:
Y por lo tanto:
La unión de una base de \(S\) con una base de \({S^ \bot }\) es base de \(V\). Esto se aplica para extender una base de \(S\;\)a una base de \(V\), como muestra el siguiente ejemplo.
Ejemplo
Sea \(S = \left\{ {\left( {{x_1},{x_2},{x_3},{x_4}} \right) \in {\mathbb{R}^4}\;:\;\;{x_1} + {x_4} = 0\;\;,\;\;{x_1} – {x_2} + 3{x_4} = 0\;} \right\}\).
Hallar una base de \(S\) y extenderla a una base de \({\mathbb{R}^4}\).
Resolución
Buscamos una base de S, por ejemplo:
\[{B_S} = \left\{ {\;\left( {1, – 2,0, – 1} \right),\;\left( {0,0,1,0} \right)} \right\}\]
Como \(dim\left( S \right) = 2\), podemos anticipar que: \(dim({S^ \bot }\) )= 4 – 2 = 2
A partir de la base de S, obtenemos las ecuaciones de \({S^ \bot }\):
\[{S^ \bot }:\left\{ {\begin{array}{*{20}{c}}{{x_1} – 2{x_2} – {x_4} = 0}\\{{x_3} = 0}\end{array}} \right.\]
Y hallamos una base de \({S^ \bot }\) , por ejemplo:
\[{B_{{S^{ \bot \;}}}} = \{ \;\left( {2,1,0,0} \right),\;(\left( {0,1,0, – 2} \right)\} \]
Entonces uniendo las bases de \(S\) y \({S^ \bot }\) resulta:
\(B = \left\{ {\left( {1, – 2,0, – 1} \right),\left( {0,0,1,0} \right),\left( {2,1,0,0} \right),\left( {0,1,0, – 2} \right)} \right\}\) base de \({\mathbb{R}^4}\)
Ejercicio para el lector 7
Dados los siguientes subespacios de \({\mathbb{R}^4}\):
\(S = \left\{ {\left( {{x_1},{x_2},{x_3},{x_4}} \right)\;:\;\;{x_1} = 0\;\;,\;\;{x_2} + 2{x_3} = 0\;} \right\}\) y \(W = gen\left\{ {\;\left( {1,0,0,0} \right),\left( {2,3,k,0} \right)} \right\}\)
Hallar los valores de \(k\) para los cuales \(W = \;{S^ \bot }\).

