Espacio solución de un sistema homogéneo
Consideremos un sistema homogéneo \(AX\; = \;0\), con \(A \in {\mathbb{R}^{mxn}}\).
Sea \({S_h} = \left\{ {\;X \in {\mathbb{R}^{nx1}}\;:AX = \;0\;} \right\}\), el conjunto solución del sistema.
1) \(X\; = \;0\) pertenece a \({S_h}\) (solución trivial del sistema).
2) Sean \({X_1}\) y \({X_2}\) soluciones del sistema.
\(A\left( {{X_1}\; + \;{X_2}} \right) = \;A{X_1}\; + \;A{X_2} = 0\; \Rightarrow \;{X_1}\; + \;{X_2}\) también es solución
3) Sea \(X\) una solución, y \(k\) un número real.
\(A\left( {kX} \right)\; = k\left( {AX} \right) = k0 = 0\) \(kX\) también es solución
Por lo tanto:
Si el sistema (homogéneo) es compatible determinado, la única solución es la trivial. En ese caso, \(dim\left( {{S_h}} \right)\; = \;0\)
¿De qué dependerá la dimensión de \({S_h}\) para una matriz \(A\) dada?
Ejercicio para el lector 1
Dado el sistema homogéneo cuya matriz de coeficientes es
\[A = \left( {\begin{array}{*{20}{c}}1&1&1&0\\1&0&{ – 1}&1\\0&3&6&k\end{array}} \right)\]
a) Determinar la dimensión del espacio solución y el rango de \(A\) de acuerdo con los valores de \(k\).
b) Para \(k\; = \;0\) hallar una base del espacio solución.
Propiedad
Sea \({S_h}\) el espacio solución del sistema homogéneo \(AX = 0\), con \(A \in {\mathbb{R}^{mxn}}\). Puede demostrarse que:
\[dim\left( {{S_h}} \right)\; = \;n\;–\;rg\left( A \right)\]
Les pedimos que comprueben esta propiedad en el ejercicio resuelto previamente.
Nota: El conjunto solución de un sistema homogéneo \(AX = 0\) se denomina espacio nulo de la matriz A.
Relación entre las soluciones de \(AX = B\) y \(AX = 0\)
Consideremos los siguientes sistemas de ecuaciones:
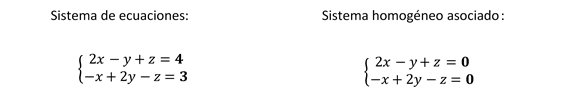
Resolvemos primero el sistema de ecuaciones original:
\[\left\{ {\begin{array}{*{20}{c}}{2x – y + z = 4}\\{ – x + 2y – z = 3}\end{array}} \right.\; \Rightarrow \;\;\;\left\{ {\begin{array}{*{20}{c}}{ – 6 + 4y – 2z – y + z = 4}\\{x = 2y – z – 3}\end{array}} \right.\; \Rightarrow \;\;\left\{ {\begin{array}{*{20}{c}}{z = – 10 + 3y}\\{x = – y + 7}\end{array}} \right.\]
Luego el conjunto solución es:
\[\left( {x,y,z} \right) = \left( { – y + 7,\;\;\;y\;\;,\; – 10 + 3y} \right) = y\left( { – 1,1,3} \right) + \left( {7,0, – 10} \right)\]
\[S = \left\{ {\left( {x,y,z} \right) \in {\mathbb{R}^3}\;|\;\;\left( {x,y,z} \right) = \lambda \left( { – 1,1,3} \right) + \left( {7,0, – 10} \right)} \right\}\]
Geométricamente, el conjunto solución es una recta que no pasa por el origen.
Resolvamos ahora el sistema homogéneo asociado:
\[\left\{ {\begin{array}{*{20}{c}}{2x – y + z = 0}\\{ – x + 2y – z = 0}\end{array}} \right.\; \Rightarrow \;\;\left\{ {\begin{array}{*{20}{c}}{4y – 2z – y + z = 0}\\{x = 2y – z}\end{array}} \right.\; \Rightarrow \;\;\left\{ {\begin{array}{*{20}{c}}{z = 3y}\\{x = – y}\end{array}} \right.\]
Luego el conjunto solución es:
\[\left( {x,y,z} \right) = \left( { – y,y,3y} \right) = y\left( { – 1,1,3} \right)\]
\[{S_h} = \left\{ {\left( {x,y,z} \right)|\;\left( {x,y,z} \right) = \lambda \left( { – 1,1,3} \right)} \right\}\]
Se trata de una recta paralela a la anterior, que pasa por el origen.
Notemos que tal como establecimos previamente, el conjunto solución de un sistema homogéneo es un subespacio.
¿Qué relación existe entre los conjuntos solución del sistema original y de su homogéneo asociado?
En la siguiente gráfica se muestran las soluciones de los sistemas. En naranja la recta solución del sistema no homogéneo, y en violeta la recta solución del sistema homogéneo:
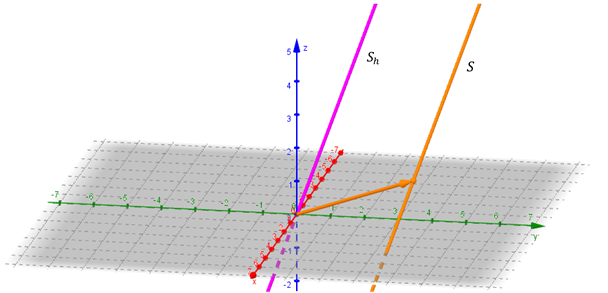
Son dos rectas paralelas: la recta que es solución del sistema homogéneo pasa por el origen y la recta que es solución del sistema no homogéneo no pasa por el origen.
Observamos que:
![]()
\[ \Rightarrow \;\;S = {S_h} + {X_p}\]
A continuación veremos un conjunto de propiedades que permiten generalizar este resultado para un sistema de ecuaciones lineales \(AX = B\) con \(A \in {\mathbb{R}^{m \times n}},\;\;B \in {\mathbb{R}^{m \times 1}}\):
Propiedad 1
La diferencia de dos soluciones particulares es solución del sistema homogéneo asociado.
Si \({X_1}\) y \({X_2}\) son dos soluciones particulares del sistema \(AX = B\), entonces se cumple que:
\[A{X_1} = B\]
\[A{X_2} = B\]
Restando miembro a miembro:
\[A{X_1} – A{X_2} = 0\]
\[ \Rightarrow \;A\left( {{X_1} – {X_2}} \right) = 0\]
Por lo tanto \({X_1} – {X_2}\) es solución de \(AX = 0\)
Propiedad 2
La suma de una solución particular de \(AX = B\) y una solución del homogéneo asociado, es solución de \(AX = B\).
Sean:
- \({X_p}\) una solución particular de \(AX = B\)
- \({X_h}\) una solución del sistema homogéneo asociado.
Queremos probar que \(\left( {{X_p} + {X_h}} \right)\) es solución de \(AX = B\)
\[A\left( {{X_p} + {X_h}} \right) = A{X_p} + A{X_h} = B + 0 = B\]
Propiedad 3
En la propiedad anterior habíamos probado que \(\left( {{X_p} + {X_h}} \right)\) es solución de \(AX = B\). Recíprocamente:
Cualquier solución del sistema \(AX = B\) puede expresarse como \({X_p} + {X_h}\), siendo \({X_p}\) una solución particular del sistema y \({X_h}\) una solución del homogéneo asociado.
Sea \(X\) una solución del sistema \(AX = B\), entonces:
\[X = \left( {X – {X_p}} \right) + {X_p}\]
Por propiedad 1, \(\left( {X – {X_p}} \right)\) es solución del homogéneo asociado, por lo tanto:
\[X = {X_h} + {X_p}\]
A partir de las propiedades 2 y 3 se deduce que:
\[S = {X_p} + {S_h} = \left\{ {{X_p} + {X_h}\;\;:\;{X_h} \in {S_h}\;} \right\}\]
Ejemplo 1
Consideremos el siguiente sistema de ecuaciones lineales no homogéneo:
\[\left\{ {\begin{array}{*{20}{c}}{x + y – z = 2}\\{ – y + z = 1}\\{2x + y – z = 5}\end{array}} \right.\;\]
Resolviendo resulta:
\[ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{z = 1 + y}\\{x = 3}\end{array}} \right.\;\]
El conjunto solución es:
\[\left( {x,y,z} \right) = \left( {\;\;\;3\;,\;y,\;\;\;1 + y\;} \right) = \left( {3,0,1} \right) + y\left( {0,1,1} \right)\]
\[S = \left\{ {\left( {x,y,z} \right) \in {\mathbb{R}^3}\;\;|\;\;\left( {x,y,z} \right) = \lambda \left( {0,1,1} \right) + \left( {3,0,1} \right)} \right\}\]
Según la propiedad vista anteriormente \({S_h} = \left\{ {\lambda \left( {0,1,1} \right)} \right\}\) es solución del sistema homogéneo asociado y \({X_p} = \left( {3,0,1} \right)\) es una solución particular del sistema no homogéneo.
Ejemplo 2
Retomemos el sistema de ecuaciones que trabajamos en un ejemplo anterior:
\[\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} + {x_4} = 3}\\{{x_3} – {x_4} = 2}\\{{x_1} + {x_2} – {x_3} + 2{x_4} = 1}\end{array}} \right.\]
Habíamos llegado al siguiente conjunto solución:
\[S = \left\{ {\left( {{x_1},{x_2},{x_3},{x_4}} \right) = \left( {3 – {x_4} – {x_2},{x_2},2 + {x_4},{x_4}} \right)\;\;\;,\;{\rm{\;\;con\;\;}}\;{x_2},{x_4} \in \mathbb{R}} \right\}\]
Observemos que el conjunto solución puede expresarse de la siguiente forma:
\[\left( {{x_1},{x_2},{x_3},{x_4}} \right) = \color{#A0F}{{x_2}\left( { – 1,1,0,0} \right) + {x_4}\left( { – 1,0,1,1} \right)} + \color{red}{\left( {3,0,2,0} \right)}\]
Dejamos a cargo del lector comprobar que:
- \(\color{red}{\left( {3,0,2,0} \right)}\) es solución del sistema
- \(\color{#A0F}{\left( { – 1,1,0,0} \right)\;\;{\rm{y\;\;}}\;\left( { – 1,0,1,1} \right)}\)
son soluciones del sistema homogéneo asociado \(AX = 0\)
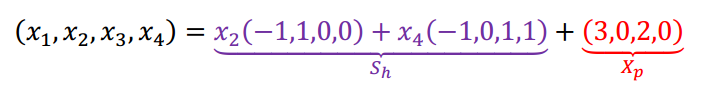
\[S = {\color{#A0F}{S_h}} + {\color{red}{X_p}}\]
Número de variables libres de un sistema
Recordemos que:
El sistema \(AX = B\) es compatible \( \Leftrightarrow \) \(b \in Col\left( A \right)\) \( \Leftrightarrow \) \(rg\left( A \right) = rg\left( {A’} \right)\)
Supongamos que \(B \in Col\left( A \right)\), es decir que el sistema es compatible, ¿Cuántas soluciones tiene?
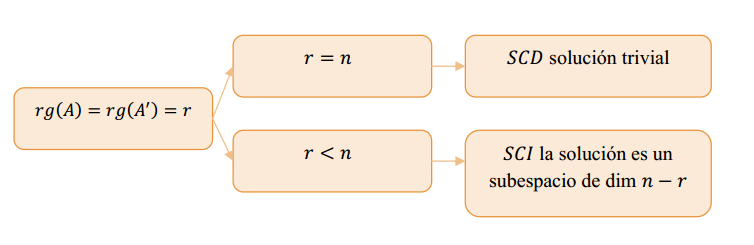
Sea \(rg\left( A \right) = rg\left( {A’} \right) = r\)
Si \(n\) es el número de incógnitas, puede demostrarse que:
- Si \(r = n\), el sistema tiene solución única (SCD)
- Si \(r < n\), el sistema admite infinitas soluciones (SCI), con \(n – r\) variables libres
Observación: El número de variables libres es igual a la dimensión del espacio solución del sistema homogéneo asociado.
Ejemplo
Analizar cada uno de los siguientes sistemas de ecuaciones, e indicar el número de variables libres.
a) \(\left\{ {\begin{array}{*{20}{c}}{x + y + z = 0}\\{x – y = 1}\\{z = 3}\end{array}} \right.\)
b) \(\left\{ {\begin{array}{*{20}{c}}{x + y + z = 0}\\{x – y = 1}\\{2x + z = 1}\end{array}} \right.\)
c) \(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} + {x_3} + {x_4} = 1}\\{{x_2} – {x_4} = 0}\\{{x_1} + {x_3} + 2{x_4} = 1}\end{array}} \right.\)
Resolución
Ítem a
\[\left\{ {\begin{array}{*{20}{c}}{x + y + z = 0}\\{x – y = 1}\\{z = 3}\end{array}} \right.\]
Realicemos el análisis a partir del rango de \(A\) y de \(A’\):
\[\left( {\begin{array}{*{20}{c}}1&1&1&0\\1&{ – 1}&0&1\\0&0&3&3\end{array}} \right)\mathop \to \limits_{{F_2} \to {F_2} – {F_1}} \left( {\begin{array}{*{20}{c}}1&1&1&0\\0&{ – 2}&{ – 1}&1\\0&0&3&3\end{array}} \right)\]
Como \(rg\left( A \right) = rg\left( {A’} \right) = n = 3\) entonces el sistema es SCD. No hay variables libres.
Ítem b
\[\left\{ {\begin{array}{*{20}{c}}{x + y + z = 0}\\{x – y = 1}\\{2x + z = 1}\end{array}} \right.\]
Escalonamos \(A’\) para hallar \(rg\left( A \right)\) y :
\[\;\;\left( {\begin{array}{*{20}{c}}1&1&1&0\\1&{ – 1}&0&1\\2&0&1&1\end{array}} \right)\mathop \to \limits_{\begin{array}{*{20}{c}}{{F_2} \to {F_2} – {F_1}}\\{{F_3} \to {F_3} – 2{F_1}}\end{array}} \left( {\begin{array}{*{20}{c}}1&1&1&0\\0&{ – 2}&{ – 1}&1\\0&{ – 2}&{ – 1}&1\end{array}} \right)\mathop \to \limits_{{F_3} \to {F_3} – {F_2}} \left( {\begin{array}{*{20}{c}}1&1&1&0\\0&{ – 2}&{ – 1}&1\\0&0&0&0\end{array}} \right)\]
Al escalonar \(A’\) se elimina una de las filas. Luego:
\[rg\left( A \right) = rg\left( {A’} \right) = 2\;\;\;\;\;{\rm{y\;\;}}\;\;\;\;n = 3 \Rightarrow \;\;SCI\;con\;una\;variable\;libre\]
Le proponemos al lector: hallar el conjunto solución, comprobar que el sistema es un SCI con una variable libre, e indicar una base de \({S_h}\).
Ítem c
\[\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} + {x_3} + {x_4} = 1}\\{{x_2} – {x_4} = 0}\\{{x_1} + {x_3} + 2{x_4} = 1}\end{array}} \right.\]
Escalonamos \(A’\) para hallar \(rg\left( A \right)\) y :
\[\left( {\begin{array}{*{20}{c}}1&1&1&1&1\\0&1&0&{ – 1}&0\\1&0&1&2&1\end{array}} \right)\mathop \to \limits_{{F_3} \to {F_3} – {F_1}} \left( {\begin{array}{*{20}{c}}1&1&1&1&1\\0&1&0&{ – 1}&0\\0&{ – 1}&0&1&0\end{array}} \right)\mathop \to \limits_{{F_3} – {F_3} + {F_2}} \left( {\begin{array}{*{20}{c}}1&1&1&1&1\\0&1&0&{ – 1}&0\\0&0&0&0&0\end{array}} \right)\]
\[rg\left( A \right) = rg\left( {A’} \right) = 2\;\;{\rm{y}}\;\;\;n = 4\;\; \Rightarrow \;SCI\;con\;dos\;variables\;libres.\]
Le proponemos al lector: hallar el conjunto solución, comprobar que el sistema es un SCI con dos variables libres, e indicar una base de \({S_h}\).
EPL 2
Dado el siguiente sistema de ecuaciones:
\[\left\{ {\begin{array}{*{20}{c}}{{x_1} + 2{x_3} + {x_4} = 5}\\{{x_1} + {x_2} + 3{x_3} – {x_4} = 1}\\{{x_2} + {x_3} + h{x_4} = k}\end{array}} \right.\]
1) Analizar el rango de \(A\) (matriz de coeficientes) de acuerdo con el valor de \(h\).
Indicar en cada caso cuál es la dimensión del sistema homogéneo asociado.
2) Para \(h = – 2\) obtener los valores de \(k\) para los cuales el sistema es compatible.
Resolver el sistema y expresar \(S = {X_p} + {S_h}\).
Obtener una base de \({S_h}\).
Resumen
Sea el sistema de ecuaciones \(AX = B\), con \(A \in {\mathbb{R}^{m \times n}}\;\;,\;\;\;X \in {\mathbb{R}^{n \times 1}}\;\;,\;\;B \in {\mathbb{R}^{m \times 1}}\), cuya matriz ampliada es:
\[A’ = \left( {{A_1}\;\;\;\;{A_2}\;\;\;{A_3}\;\; \ldots \;\;\;{A_n}\;\;\;\;B} \right)\]
El siguiente esquema resume el análisis de compatibilidad que realizamos previamente:
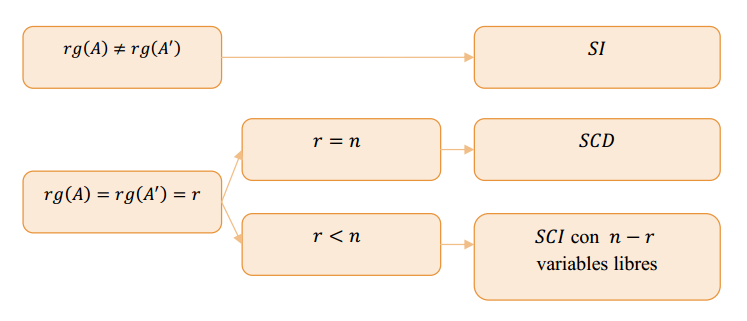
En el caso particular de un sistema homogéneo \(AX = 0\):