Definición y propiedades de las transformaciones lineales

¿Qué son las transformaciones lineales?

En primer lugar, una transformación lineal es una función. Por ser función, tiene su dominio y su codominio, con la particularidad de que éstos son espacios vectoriales. Tenemos dos espacios vectoriales \(V\) y \(W\), y una función que va de \(V\) a \(W\). O sea una regla de asignación que transforma vectores de \(V\) en vectores de \(W\). Pero no toda función que transforme vectores de \(V\) en vectores de \(W\) es una transformación lineal. Debe cumplir ciertas condiciones:

\(F:V \to W\) es una transformación lineal si y sólo si:

1. \(F\left( {u + v} \right) = F\left( u \right) + F\left( v \right){\rm{\;\;}}\ \ \ \ \forall u,v \in V\)
2. \(F\left( {k.v} \right) = k.F\left( v \right){\rm{\;\;\;}}\ \ \ \ \ \ \ \forall v \in V,{\rm{\;}} \ \   \forall k \in \mathbb{R}\)

Propiedades de una transformación lineal

Propiedad 1

La imagen del vector nulo del dominio \({0_V}\) es el vector nulo del codominio \({0_{w\;}}\):

\[T\left( {{0_V}} \right) = {0_w}\]

Demostración:

\[T\left( {{0_V}} \right) = T\left( {0.v} \right) = 0.T\left( v \right) = 0.w = {0_W}\]

Donde hemos expresado a \({0_V}\) como el producto del escalar \(0\) por cualquier vector del espacio vectorial \(V\), hemos usado la segunda condición que debe cumplir una transformación lineal, y finalmente hemos vuelto a usar la propiedad de espacios vectoriales sobre el producto del escalar 0 por cualquier vector.

Propiedad 2

La imagen del vector \( – v\) es igual al opuesto de la imagen de \(v\):

\[T\left( { – v} \right) = – T\left( v \right)\]

Demostración:

\[T\left( { – v} \right) = T\left( { – 1.v} \right) = – 1.T\left( v \right) = – T\left( v \right)\]

La justificación de los pasos dados en la demostración es similar a la anterior.

Propiedad 3

Consideremos \(r\) vectores del espacio vectorial \(V\):

\[{v_1},{v_2}, \ldots ,{v_r} \in V\]

Tomemos una combinación lineal en el dominio:

\[{\alpha _1}{v_1} + {\alpha _2}{v_2} + {\alpha _3}{v_3} + ..{\rm{\;}}.{\rm{\;}} + {\alpha _r}{v_r}\]

Donde \({\alpha _i} \in \mathbb{R}\).

Si aplicamos la transformación lineal \(F\) de \(V\) a \(W\), teniendo en cuenta las propiedades enunciadas en la definición, resulta:

\[F\left( {{\alpha _1}{v_1} + {\alpha _2}{v_2} + {\alpha _3}{v_3} + ..{\rm{\;}}.{\rm{\;}} + {\alpha _r}{v_r}} \right) = {\alpha _1}F\left( {{v_1}} \right) + {\alpha _2}F\left( {{v_2}} \right) + \ldots + {\alpha _r}F\left( {{v_r}} \right){\rm{\;}}\]

Es decir que una transformación lineal «transporta» combinaciones lineales de \(V\) a \(W\), conservando los escalares de la combinación lineal.

Ejemplo 1

Analizar si la siguiente función es una transformación lineal:

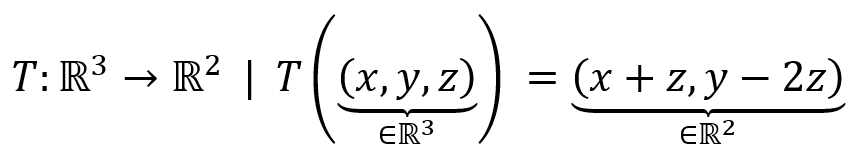
Resolución

Controlemos primero que el transformado del \({0_V}\) sea el \({0_W}\). Ésta es una condición necesaria: si no se cumpliera, no sería transformación lineal. Como \(T\left( {\left( {0,0,0} \right)} \right) = \left( {0,0} \right)\), la función dada es «candidata» a ser transformación lineal. Para demostrar que es una transformación lineal tenemos que comprobar las condiciones dadas en la definición.

Condición 1: \(T\left( {u + v} \right) = T\left( u \right) + T\left( v \right){\rm{\;\;}}\forall u,v \in V\)

Tomemos dos vectores de \({\mathbb{R}^3}\)

\[u = \left( {{u_1},{u_2},{u_3}} \right)\]

\[v = \left( {{v_1},{v_2},{v_3}} \right)\]

Veamos si

\[T\left( {u + v} \right) = T\left( u \right) + T\left( v \right)\]

Primero hacemos la suma de \(u\) y \(v\):

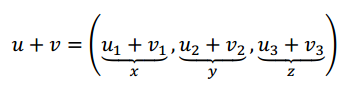
Y ahora aplicamos \(T\):

\[T\left( {u + v} \right) = \left( {{u_1} + {v_1} + {u_3} + {v_3}{\rm{\;}},{\rm{\;}}{u_2} + {v_2} – 2{u_3} – 2{v_3}} \right)\]

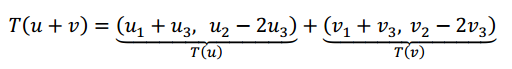
\[T\left( {u + v} \right) = T\left( u \right) + T\left( v \right)\]

En conclusión: se cumple la primera de las condiciones.

Nos faltaría la otra propiedad.

Condición 2: \(\;\;T\left( {k.v} \right) = k.T\left( v \right){\rm{\;\;\;}}\forall v \in V,{\rm{\;}}\forall k \in \mathbb{R}\)

\[T\left( {k.v} \right) = T\left( {\left( {k{v_1},k{v_2},k{v_3}} \right)} \right) = \left( {k{v_1} + k{v_3},{\rm{\;}}k{v_2} – 2k{v_3}} \right)\]

\[ = k.\left( {{v_1} + {v_3},{v_2} – 2{v_3}} \right) = k.T\left( v \right)\]

Como \(T\) cumple las dos condiciones, es una transformación lineal.

Ejemplo 2

Analizar si la siguiente función es una transformación lineal:

\[F:{P_2} \to \mathbb{R}\;\;\;|\;\;F\left( p \right) = p\left( 0 \right)\]

Observación: con \({P_2}\) se designa al conjunto de todos los polinomios de grado menor o igual que dos, con el polinomio nulo.

Resolución

Entonces a un polinomio \(p\) de grado menor o igual que dos, le aplicamos la función \(F\) y obtenemos un número real que proviene de evaluar el polinomio en \(x = 0\).

Por ejemplo evaluemos la transformación en \({x^2} – 1\):

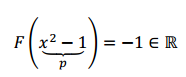
Veamos si el vector nulo del espacio vectorial \({P_2}\) va al \(0 \in \mathbb{R}\) (es condición necesaria).

El polinomio cero es:

\[{0_{{P_2}}} = {\rm{\;}}0{x^2} + 0x + 0\]

¿Cuánto vale el polinomio nulo evaluado en \(0\)? \(0\)

\[{0_{{P_2}}}\left( 0 \right) = {0.0^2} + 0.0 + 0 = 0\]

Entonces la condición necesaria para este ejercicio se cumple, porque \(F\left( {{0_{{P_2}}}} \right) = 0\)

Primera condición \(\;F\left( {u + v} \right) = F\left( u \right) + F\left( v \right){\rm{\;\;}}\forall u,v \in V\)

Para que sea transformación lineal se debe cumplir la primera condición. Veamos qué pasa con el transformado de la suma:

\[\left( {p + q} \right) \in {P_2}\]

\[F\left( {p + q} \right) = \left( {p + q} \right)\left( 0 \right) = p\left( 0 \right) + q\left( 0 \right)\]

Observación: evaluar una suma de funciones en \(0\), es evaluar cada una en \(0\) y sumarlas. Esto no es una particularidad de los polinomios, sino que se corresponde con la definición de suma de funciones:

Para cualquier función: \(\left( {f\; + \;g} \right)\;\left( x \right)\; = \;f\left( x \right)\; + \;g\left( x \right)\), para todo \(x\) perteneciente al dominio de \(f\) y de \(g\).

Otra forma de pensar la misma propiedad. Si consideramos

\(p\left( x \right) = a{x^2} + bx + c\)        y        \(q\left( x \right) = d{x^2} + ex + f\)

\[p{\rm{\;}} + {\rm{\;}}q{\rm{\;}} = {\rm{\;}}\left( {a + d} \right){x^2}{\rm{\;}} + {\rm{\;}}\left( {b + e} \right){\rm{\;}}x{\rm{\;}} + {\rm{\;}}\left( {c + f} \right)\]

\[F\left( {p + q} \right){\rm{\;}} = {\rm{\;}}c{\rm{\;}} + {\rm{\;}}f{\rm{\;}} = {\rm{\;}}F\left( p \right){\rm{\;}} + {\rm{\;}}F\left( q \right)\]

Por los dos caminos arribamos a la misma conclusión.

Segunda condición \(F\left( {k.v} \right) = k.F\left( v \right){\rm{\;\;\;}}\forall v \in V,{\rm{\;}}\forall k \in \mathbb{R}\)

Veamos si se cumple la segunda condición. Para esto podemos recordar que dada una función \(f\left( x \right)\) y un escalar \(k\), la función \(\left( {k.f} \right)\left( x \right)\) se define como \(k.f\left( x \right)\). De esta forma podemos decir:

• \(p \in {P_2}{\rm{\;\;\;}},{\rm{\;\;\;}}k \in \mathbb{R}\)
• \(F\left( {k.p} \right) = \left( {k.p} \right)\left( 0 \right) = k.p\left( 0 \right) = k.F\left( p \right)\)

Otra forma de verlo es escribir a un polinomio \(p \in {P_2}\) de forma genérica y aplicar la transformación sobre \(k.p\):

\[p\left( x \right) = a{x^2} + bx + c\]

\[F\left( {k.p} \right) = F\left( {k.\left( {a{x^2} + bx + c} \right)} \right) = F\left( {k.a{x^2} + k.bx + k.c} \right) = k.c = k.F\left( p \right)\]

Ejemplo 3

Consideremos la transformación lineal:

\[T:{R^3} \to {R^3}{\rm{\;\;}},{\rm{\;\;\;}}T\left( v \right) = v \times {w_0}{\rm{\;}}\]

Siendo \({w_0}\) un vector fijo y \(\;v\) un vector cualquiera de \({R^3}\). Veamos que se trata de una transformación lineal.

Condición 1: \(T\left( {u + v} \right) = T\left( u \right) + T\left( v \right){\rm{\;\;}}\forall u,v \in V\)

Para ver que se cumple esta condición usaremos la propiedad distributiva del producto vectorial respecto de la suma de vectores:

\[{v_1},{v_2} \in {R^3},{\rm{\;\;\;\;}}T\left( {{v_1} + {v_2}} \right) = \left( {{v_1} + {v_2}} \right) \times {w_0} = {v_1} \times {w_0} + {v_2} \times {w_0} = T\left( {{v_1}} \right) + T\left( {{v_2}} \right)\]

Condición 2: \(T\left( {k.v} \right) = k.T\left( v \right){\rm{\;\;\;}}\forall v \in V,{\rm{\;}}\forall k \in \mathbb{R}\)

Para ver que se cumple esta condición podemos extraer el escalar:

\[T\left( {k.v} \right) = \left( {kv} \right) \times {w_0} = k.\left( {v \times {w_0}} \right) = k.T\left( v \right)\]

Ejemplo 4

Consideremos las siguientes transformaciones:

\[{T_1}:{\mathbb{R}^2} \to {\mathbb{R}^2}{\rm{\;\;\;}},{\rm{\;\;\;}}{T_1}\left( {\left( {x,y} \right)} \right) = \left( {2x – 1,y} \right)\]

\[{T_2}:{\mathbb{R}^2} \to {\mathbb{R}^2}{\rm{\;\;\;}},{\rm{\;\;\;\;}}{T_2}\left( {\left( {a,b} \right)} \right) = \left( {{a^2},b} \right)\]

¿Cómo analizamos si son o no son transformaciones lineales?

Para la primera transformación basta con ver que la imagen de \(\left( {0,0} \right)\) es \(\left( { – 1,0} \right)\). No se cumple una de las propiedades de las transformaciones lineales, entonces no es una transformación lineal. La segunda transformación no cumple con la segunda condición ya que:

• \({T_2}\left( {k.(a,b} \right)) = \left( {{k^2}.{a^2},kb} \right)\)
• \(k.{T_2}\left( {a,b} \right) = \left( {k.{a^2},kb} \right)\)

Luego, como no se cumple que \(T\left( {k.v} \right) = k.T\left( v \right)\) podemos afirmar que \({T_2}\) no es una transformación lineal.

Videos relacionados con transformaciones lineales