Núcleo, imagen y teorema de las dimensiones
Núcleo de una transformación lineal
Sea \(F:V \to W\;\) una transformación lineal. Llamamos núcleo de \(F\) al conjunto de vectores del dominio cuya imagen por \(F\) es el \({0_W}\). \[Nu\left( F \right) = \left\{ {v \in V{\rm{\;}}|{\rm{\;}}F\left( v \right) = {0_W}} \right\}\] El núcleo de una transformación lineal es un subespacio de \(V\).
Imagen de una transformación lineal
Llamamos imagen de \(F\) al conjunto de vectores de \(W\) que son imagen de algún vector de \(V\). \[Im\left( F \right) = \left\{ {w \in W{\rm{\;}}|{\rm{\;}}w = F\left( v \right){\rm{\;}},{\rm{\;}}v \in V} \right\}\] La imagen es un subespacio de W.
Ejemplo 1
Dada la siguiente transformación lineal \[T:{\mathbb{R}^3} \to {\mathbb{R}^3}{\rm{\;\;\;}},{\rm{\;}}T\left( {\left( {x,y,z} \right)} \right) = \left( {x – 2y{\rm{\;}},{\rm{\;}}0{\rm{\;}},{\rm{\;}}2x – 4y} \right)\] Buscar el núcleo, la imagen, y determinar sus dimensiones.
Resolución
Para determinar el núcleo planteamos:
\(\left( {x,y,z} \right)\) está en el núcleo \( \Leftrightarrow \) \(T\left( {\left( {x,y,z} \right)} \right){\rm{\;}} = {\rm{\;}}\left( {0,0,0} \right)\)
\[\left( {x – 2y{\rm{\;}},{\rm{\;}}0{\rm{\;}},{\rm{\;}}2x – 4y} \right) = \left( {0,0,0} \right) \Rightarrow {\rm{\;}}\left\{ {\begin{array}{*{20}{c}}{x – 2y = 0}\\{2x – 4y = 0}\end{array}} \right. \Rightarrow x = 2y\] Esto implica que la primera componente debe ser el doble de la segunda y que la tercera componente no tiene restricciones. Es un error común, en este punto, suponer que como «no aparece \(z\)», entonces \(z = 0\). Pero es importante notar que si «no aparece \(z\)» esto significa que no existen restricciones sobre esa componente. La forma de un vector del núcleo sería: \[\left( {2y,y,z} \right)\] Aplicando propiedades lo podemos escribir: \[y.\left( {2,1,0} \right) + z.\left( {0,0,1} \right)\] Luego el núcleo es: \[Nu\left( T \right) = \left\{ {\left( {x,y,z} \right) \in {\mathbb{R}^3}{\rm{\;}}|{\rm{\;}}x = 2y{\rm{\;}}} \right\} = gen\left\{ {\left( {2,1,0} \right),\left( {0,0,1} \right)} \right\}\] Y una base del núcleo es: \[{B_{Nu}} = \left\{ {\left( {2,1,0} \right),\left( {0,0,1} \right)} \right\}\] La imagen la podemos obtener aplicando propiedades sobre la expresión que define la transformación lineal: \[\left( {x – 2y{\rm{\;}},{\rm{\;}}0{\rm{\;}},{\rm{\;}}2x – 4y} \right) = x.\left( {1,0,2} \right) + y.\left( { – 2,0, – 4} \right)\] Los vectores \(\left( {1,0,2} \right)\) y \(\left( { – 2,0, – 4} \right)\) son linealmente dependientes. Entonces tomamos uno de ellos para la base de la imagen: \[{B_{Im}} = \left\{ {\left( {1,0,2} \right)} \right\}\] Finalmente podemos responder sobre las dimensiones de núcleo e imagen, porque hemos obtenido bases de estos subespacios: \[{\rm{\;}}dim\left( {Nu} \right) = 2\] \[dim\left( {Im} \right) = 1\]
Ejemplo 2
Dada la siguiente transformación lineal \[F:{\mathbb{R}^3} \to {\mathbb{R}^{2 \times 2}}{\rm{\;\;\;\;}}F\left( {\left( {x,y,z} \right)} \right) = \left( {\begin{array}{*{20}{c}}{x + y}&{x – z}\\0&{y + z}\end{array}} \right)\] Buscar el núcleo, la imagen, y determinar sus dimensiones.
Resolución
Para determinar el núcleo planteamos: \(\left( {x,y,z} \right)\) está en el núcleo \( \Leftrightarrow \) \(F\left( {x,y,z} \right) = \left( {\begin{array}{*{20}{c}}0&0\\0&0\end{array}} \right)\) \[\left( {\begin{array}{*{20}{c}}{x + y}&{x – z}\\0&{y + z}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0&0\\0&0\end{array}} \right) \Rightarrow {\rm{\;}}\left\{ {\begin{array}{*{20}{c}}{x + y = 0}\\{x – z = 0}\\{y + z = 0}\end{array}} \right.{\rm{\;}} \Rightarrow x = z = – y\] Se trata de un sistema compatible indeterminado. El núcleo queda definido entonces por vectores con la forma: \[\left( { – y,y, – y} \right) = y.\left( { – 1,1, – 1} \right)\] Entonces: \[Nu\left( F \right) = \left\{ {\left( {x,y,z} \right) \in {\mathbb{R}^3}{\rm{\;}}|{\rm{\;}}x = z = – y} \right\} = gen\left\{ {\left( { – 1,1, – 1} \right)} \right\}\] \[{B_{Nu}} = \left\{ {\left( {1, – 1,1} \right)} \right\}\] La imagen la podemos obtener aplicando propiedades sobre la expresión que define la transformación lineal: \[\left( {\begin{array}{*{20}{c}}{x + y}&{x – z}\\0&{y + z}\end{array}} \right) = x.\left( {\begin{array}{*{20}{c}}1&1\\0&0\end{array}} \right) + y.\left( {\begin{array}{*{20}{c}}1&0\\0&1\end{array}} \right) + z.\left( {\begin{array}{*{20}{c}}0&{ – 1}\\0&1\end{array}} \right)\] Luego, estas tres matrices generan la imagen, porque cualquier vector de la imagen es combinación lineal de ellas. \[Im\left( T \right) = gen\left\{ {\left( {\begin{array}{*{20}{c}}1&1\\0&0\end{array}} \right),\left( {\begin{array}{*{20}{c}}1&0\\0&1\end{array}} \right),\left( {\begin{array}{*{20}{c}}0&{ – 1}\\0&1\end{array}} \right)} \right\}\] La generan, pero ¿son una base de la imagen? Observamos que las dos primeras son linealmente independientes. Pero la tercera es combinación lineal de las anteriores: \[\left( {\begin{array}{*{20}{c}}1&0\\0&1\end{array}} \right) – \left( {\begin{array}{*{20}{c}}1&1\\0&0\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0&{ – 1}\\0&1\end{array}} \right)\] Entonces una base de la imagen es: \[{B_{Im}} = \left\{ {\left( {\begin{array}{*{20}{c}}1&1\\0&0\end{array}} \right),\left( {\begin{array}{*{20}{c}}1&0\\0&1\end{array}} \right)} \right\}\] Ahora podemos responder sobre las dimensiones: \[\dim \left( {Nu} \right) = 1\] \[\dim \left( {Im} \right) = 2\] Notemos que la suma de las dimensiones de núcleo e imagen es igual a la dimensión del dominio de la transformación lineal: \[\dim \left( {{\mathbb{R}^3}} \right) = 3\] Esto no es casual, sino que se trata de un teorema que consideraremos a continuación.
Teorema de las dimensiones
El teorema de las dimensiones establece una relación aritmética sencilla entre la dimensión de \(V\) y la dimensión del núcleo y de la imagen. Sea \(F:V \to W{\rm{\;}}\) transformación lineal\(.\) Si \(dim\left( V \right) = n\) (finita) entonces: \[\dim \left( V \right) = \dim \left( {Nu\left( F \right)} \right) + \dim \left( {Im\left( F \right)} \right)\]
Ejemplo 1
Buscar el núcleo y la imagen de la siguiente transformación lineal:
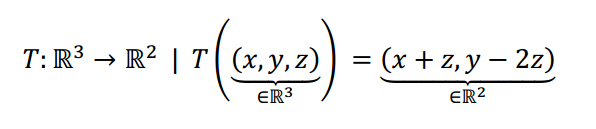
Resolución
Buscar el núcleo de la transformación lineal es buscar los vectores del dominio cuya imagen es el vector nulo del codominio: \[T\left( {\left( {x,y,z} \right)} \right) = \left( {0,0} \right) \Rightarrow \left\{ {\begin{array}{*{20}{c}}{x + z = 0}\\{y – 2z = 0}\end{array} \Rightarrow x = – z \wedge y = 2z} \right.\] Luego los vectores del núcleo son de la forma: \[\left( { – z,{\rm{\;}}2z,z} \right) = z\left( { – 1,2,1} \right)\] Así podemos escribir: \[Nu = \left\{ {\left( {x,y,z} \right) \in {\mathbb{R}^3}|{\rm{\;}}x = – z \wedge y = 2z} \right\} = gen\left\{ {\left( { – 1,2,1} \right)} \right\}\] \[{B_{Nu}} = \left\{ {\left( { – 1,2,1} \right)} \right\} \Rightarrow \dim \left( {Nu} \right) = 1\] El núcleo es una recta porque tiene dimensión 1.
¿Cuál es la dimensión de la imagen? Por el teorema de las dimensiones debe ser:
\[\dim \left( V \right) = \dim \left( {NuT} \right) + {\rm{dim}}\left( {ImT} \right)\]
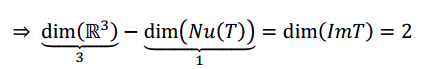
La imagen es todo el espacio \({\mathbb{R}^2}\) porque el único subespacio de dimensión 2 que está en \({\mathbb{R}^2}\) es \({\mathbb{R}^2}\).
¿Cómo se llaman las funciones cuya imagen coincide con el codominio? Sobreyectivas.
Diremos entonces que \(T\) es una transformación lineal sobreyectiva.
Ejemplo 2
Sea \(T:{\mathbb{R}^2} \to {\mathbb{R}^3}\;\) una transformación lineal,
\[T\left( {x,y} \right) = \left( {x – 2y,2x – 4y, – 2x + 4y} \right)\]
Buscar una base y la dimensión de \(Nu\left( T \right),\;Im\left( T \right)\)
Resolución
Por el teorema de las dimensiones la suma de las dimensiones del núcleo y de la imagen debe ser 2. Es decir que puede ser alguno de los siguientes escenarios:
\[2 + 0\]
\[1 + 1\]
\[0 + 2\]
Busquemos \(Nu\left( T \right)\):
\[\left( {x – 2y,2x – 4y, – 2x + 4y} \right) = \left( {0,0,0} \right) \Rightarrow {\rm{\;}}\left\{ {\begin{array}{*{20}{c}}{x – 2y = 0}\\{2x – 4y = 0}\\{ – 2x + 4y = 0}\end{array}} \right. \Rightarrow x = 2y\]
Luego podemos dar una base del núcleo y su dimensión:
\[{B_{Nu}} = \left\{ {\left( {2,1} \right)} \right\}{\rm{\;}} \Rightarrow \dim \left( {Nu} \right) = 1\]
Busquemos \(Im\left( T \right)\). Un vector está en la imagen si es el transformado de algún vector del dominio:
\[{\rm{T}}\left( {x,y} \right) = {\rm{\;}}\left( {x – 2y,2x – 4y, – 2x + 4y} \right)\]
Lo expresamos como suma de vectores separando las variables \(x\) e \(y\):
\[T\left( {x,y} \right) = \left( {x,2x, – 2x} \right) + \left( { – 2y, – 4y,4y} \right)\]
Y sacamos como escalares a las variables:
\[ = x\left( {1,2, – 2} \right) + y\left( { – 2, – 4,4} \right)\]
Este método permite obtener generadores de la imagen, que pueden ser LI o LD. Acá se ve muy claro que \(\left( { – 2, – 4,4} \right)\) = (- \(2).\left( {1,2, – 2} \right)\). Es decir que generan la imagen pero son linealmente dependientes, no es una base. Cualquiera de los dos sirve como base:
\[{B_{Im\left( T \right)}} = \left\{ {\left( {1,2, – 2} \right)} \right\} \Rightarrow \dim \left( {Im\left( T \right)} \right) = 1\]
Más adelante veremos otro método para encontrar la imagen.
Ejemplo 3
Hallar núcleo e imagen de la siguiente transformación lineal:
\[F:{P_2} \to \mathbb{R}\;|\;F\left( p \right) = p\left( 0 \right)\]
Resolución
Notemos que los números reales pueden ser entendidos como un espacio vectorial de dimensión 1.
Si \(p\left( x \right) = a{x^2} + bx + c{\rm{\;}},{\rm{\;\;}}p\left( 0 \right) = c\)
El núcleo estará formado por todos los polinomios cuyo término independiente es 0.
¿Cuál es una base para ese espacio vectorial? Podríamos describir al núcleo así:
\[Nu\left( F \right) = \left\{ {a{x^2} + bx,a,b \in \mathbb{R}} \right\}\]
Una base natural es la constituida por los vectores: \({x^2}\) y \(x\).
Entonces: \({B_{Nu}} = \left\{ {{x^2},\;\;x} \right\} \Rightarrow \dim \left( {Nu} \right) = 2\) Aplicando el teorema: \[\dim \left( {Im} \right) = 1\] Y ahora si consideramos que la imagen está incluida o es igual a \(\mathbb{R}\), entonces: \[Im\left( F \right) = \mathbb{R}\] ¿Y una base para el espacio vectorial \(\mathbb{R}\)? Puede servir cualquier número real, menos el cero. Tomamos por ejemplo: \[{B_{Im}} = \left\{ 1 \right\}\]
Los transformados de una base generan la imagen
Sea \(F:V \to W{\rm{\;transformación\;lineal}}\) , y \(B = \left\{ {{v_1}, \ldots ,{v_n}} \right\}{\rm{\;}}base{\rm{\;}}de{\rm{\;}}V\) Entonces: \[w \in Im\left( F \right) \Leftrightarrow {\rm{\;}}w = F\left( v \right),{\rm{\;}}v \in V \Leftrightarrow {\rm{\;}}w = F\left( {{a_1}{v_1} + \ldots + {\alpha _n}{v_n}{\rm{\;}}} \right)\] \[ \Leftrightarrow {\rm{\;}}w = {\alpha _1}F\left( {{v_1}} \right) + \ldots + {\alpha _n}F\left( {{v_n}} \right){\rm{\;}}\]
Hemos demostrado que:
O sea, aplicando la transformación lineal a los vectores de una base (cualquiera) del dominio, se obtiene un conjunto de generadores de la imagen: \[\left\{ {F\left( {{v_1}} \right),F\left( {{v_2}} \right),F\left( {{v_3}} \right), \ldots ,F\left( {{v_n}} \right)} \right\}{\rm{\;}}generan{\rm{\;}}Im\left( F \right)\] No estamos diciendo que constituyan una base de la imagen, sino que la generan. Ahora veremos un ejemplo sobre cómo se aplica esto:
Ejemplo 1
Sea \(F\) la siguiente transformación lineal: \[F:{\mathbb{R}^{2 \times 2}} \to {\mathbb{R}^3}{\rm{\;transformación\;lineal\;\;\;\;}},{\rm{\;\;\;\;}}F\left( {\left( {\begin{array}{*{20}{c}}a&b\\c&d\end{array}} \right)} \right) = \left( {a + b + d, – d,d} \right)\] Hallar una base de la imagen.
Resolución
Podemos elegir una base del dominio y aplicar la transformación, obteniendo así un conjunto generador de la imagen. Si son LI, ya tenemos una base de la imagen. Si son LD, tendremos que eliminar «lo que sobra» para conseguir una base. Usemos la base canónica de \({\mathbb{R}^{2 \times 2}}\): \[F\left( {\begin{array}{*{20}{c}}1&0\\0&0\end{array}} \right) = \left( {1,0,0} \right)\] \[F\left( {\begin{array}{*{20}{c}}0&1\\0&0\end{array}} \right) = \left( {1,0,0} \right)\] \[F\left( {\begin{array}{*{20}{c}}0&0\\1&0\end{array}} \right) = \left( {0,0,0} \right)\] \[F\left( {\begin{array}{*{20}{c}}0&0\\0&1\end{array}} \right) = \left( {1, – 1,1} \right)\] Entonces obtuvimos el siguiente conjunto de generadores: \[\left\{ {\left( {1,0,0} \right),\left( {0,0,0} \right),\left( {1, – 1,1} \right)} \right\}\] Nos quedamos con un conjunto linealmente independiente: \[{B_{Im}} = \left\{ {\left( {1,0,0} \right),\left( {1, – 1,1} \right)} \right\}\] Si la dimensión de la imagen es 2, puedo conocer la dimensión del núcleo. Como el dominio tiene dimensión 4, la dimensión del núcleo debe ser: \[{\rm{dim\;}}\left( V \right) – \dim \left( {Im} \right) = \dim \left( {Nu} \right) = 2\] Busquemos el núcleo: \[\left( {a + b + d, – d,d} \right) = \left( {0,0,0} \right) \Rightarrow {\rm{\;}}\left\{ {\begin{array}{*{20}{c}}{a + b + d = 0}\\{ – d = 0}\\{d = 0}\end{array} \Rightarrow d = 0{\rm{\;}} \wedge {\rm{\;}}a = – b} \right.{\rm{\;}}\forall c \in \mathbb{R}\] Y la variable \(c\) queda libre porque no aparece ninguna condición sobre ella. Entonces: \[Nu = \left\{ {\left( {\begin{array}{*{20}{c}}{ – b}&b\\c&0\end{array}} \right) \in {\mathbb{R}^{2 \times 2}}{\rm{\;\;}}|{\rm{\;\;\;}}b,c \in \mathbb{R}} \right\}\] \[{B_{Nu}} = \left\{ {\left( {\begin{array}{*{20}{c}}0&0\\1&0\end{array}} \right),\left( {\begin{array}{*{20}{c}}{ – 1}&1\\0&0\end{array}} \right)} \right\}\] Lo cual es coherente con la dimensión del núcleo que calculamos anteriormente.
Ejemplo 2
Consideremos la transformación lineal: \[T:{R^3} \to {R^3}{\rm{\;\;}},{\rm{\;\;\;}}T\left( v \right) = v \times {w_0}{\rm{\;}}\] Siendo \({w_0} = \left( {0,0,1} \right)\) un vector fijo y \(\;v\) un vector cualquiera de \({R^3}\).
a) Hallar el núcleo, una base del núcleo y su dimensión.
b) Hallar la imagen, una base de la imagen y su dimensión
Resolución
Ya analizamos anteriormente que es una trasformación lineal. Sabemos que un vector pertenece al núcleo de la transformación sí y sólo si su transformado es el vector nulo: \[\left( {x,y,z} \right) \in Nu\left( T \right) \Leftrightarrow T\left( {\left( {x,y,z} \right)} \right) = \left( {0,0,0} \right)\] Entonces transformemos a un vector genérico e igualémoslo al vector nulo para ver qué condiciones debe cumplir ese vector genérico: \[\left( {x,y,z} \right) \times \left( {0,0,1} \right) = \left( {y, – x,0} \right) = \left( {0,0,0} \right)\] Es decir que el núcleo está formado por los vectores que cumplen que \(x = 0 \wedge y = 0\). Estos son los vectores paralelos al eje \(z\). \[Nu\left( T \right) = \left\{ {\left( {x,y,z} \right) \in \mathbb{R}|\;x = 0 \wedge y = 0} \right\}\] \[{B_{Nu\left( T \right)}} = \left\{ {\left( {0,0,1} \right)} \right\}\] \[\dim \left( {Nu\left( T \right)} \right) = 1\] ¿Se podría haber pensado esto geométricamente? ¿Cuál es el conjunto de vectores tales que su producto vectorial con \(\left( {0,0,1} \right)\) es el vector nulo? Obtengamos la imagen a partir de que los transformados de una base del domino generan la imagen. \[{B_{{\mathbb{R}^3}}} = \left\{ {\left( {1,0,0} \right),\left( {0,1,0} \right),\left( {0,0,1} \right)} \right\}\] \[T\left( {\left( {1,0,0} \right)} \right) = \left( {1,0,0} \right) \times \left( {0,0,1} \right) = \left( {0, – 1,0} \right)\] \[T\left( {\left( {0,1,0} \right)} \right) = \left( {0,1,0} \right) \times \left( {0,0,1} \right) = \left( {1,0,0} \right)\] \[T\left( {\left( {0,0,1} \right)} \right) = \left( {0,0,1} \right) \times \left( {0,0,1} \right) = \left( {0,0,0} \right)\] Luego: \[Im\left( T \right) = gen\left\{ {\left( {0, – 1,0} \right),\left( {1,0,0} \right),\left( {0,0,0} \right)} \right\}\] Sacando el vector nulo obtenemos un conjunto linealmente independiente, y así una base de la imagen: \[{B_{Im\left( T \right)}} = \left\{ {\left( {0, – 1,0} \right),\left( {1,0,0} \right)} \right\}{\rm{\;}}\] \[\dim \left( {Im\left( T \right)} \right) = 2\] ¿Se podría haber pensado esto geométricamente? ¿Cuál es el conjunto de vectores que se obtiene al hacer el producto vectorial de cualquier vector \(v \in {\mathbb{R}^3}\) con \(\left( {0,0,1} \right)\)? ¿Cómo generalizarían para un \({w_0}\) cualquiera, no nulo?
En el siguiente archivo de GeoGebra se puede explorar la situación. Hay tres vectores:
- Un vector fijo, en color negro.
- Un vector móvil en color verde.
- Un vector rojo que es el resultado del producto vectorial entre los otros dos.
Te proponemos que muevas el vector verde y veas que se va obteniendo cómo el conjunto de vectores que se obtienen de los sucesivos productos vectoriales:
Clasificación de las transformaciones lineales
Monomorfismos: Transformaciones lineales inyectivas
Recordemos que una función \(F:\;A \to B\) es inyectiva si verifica la siguiente propiedad: \[F\left( {{x_1}} \right) = {\rm{\;}}F\left( {{x_2}} \right) \Rightarrow {x_1} = {x_2}{\rm{\;\;\;}}\forall {x_1},{x_2} \in A\] En el caso particular de las T.L., puede demostrarse que:
Sea \(F:\;V \to \;W\) una transformación lineal,
Epimorfismos: Transformaciones lineales sobreyectivas
Isomorfismos: Transformaciones lineales biyectivas
\(F:{\rm{\;}}V \to {\rm{\;}}W{\rm{\;}}\) es biyectiva (isomorfismo) \( \Leftrightarrow {\rm{\;\;}}Nu\left( F \right) = \left\{ {{0_V}} \right\}{\rm{\;}} \wedge {\rm{\;}}Im\left( F \right){\rm{\;}} = {\rm{\;}}W\)
Ejemplo 1
Consideremos la siguiente transformación lineal \(T:{\mathbb{R}^2} \to {\mathbb{R}^3}\;\;\;T\left( {\left( {x,y} \right)} \right) = \left( {x + y,x – y,2x} \right)\) Saquemos el núcleo de la transformación: \[\left( {x,y} \right) \in Nu\left( T \right) \Leftrightarrow T\left( {\left( {x,y} \right)} \right) = \left( {0,0,0} \right)\] \[\left( {x + y,x – y,2x} \right) = \left( {0,0,0} \right){\rm{\;\;}} \Rightarrow {\rm{\;\;}}x = 0 \wedge y = 0\] Entonces por la propiedad enunciada anteriormente podemos decir que \(T\) es un monomorfismo. Por el teorema de las dimensiones resulta: \[\dim \left( {Im} \right) = \dim \left( {{\mathbb{R}^2}} \right) – \dim \left( {Nu} \right) = 2 – 0 = 2\] Como la dimensión de la imagen es 2, entonces no es un epimorfismo (sobreyectiva). Conclusión: \(T\) es un monomorfismo.
Ejemplo 2
Consideremos la transformación lineal \[F:{\mathbb{R}^{2 \times 2}} \to {\mathbb{R}^2}{\rm{\;\;\;\;}},{\rm{\;\;\;\;}}F\left( {\left( {\begin{array}{*{20}{c}}a&b\\c&d\end{array}} \right)} \right) = \left( {a + b, – d} \right)\] Busquemos su imagen: \[\left( {a + b, – d} \right) = a.\left( {1,0} \right) + b.\left( {1,0} \right) + d.\left( {0, – 1} \right)\] \[ \Rightarrow Im\left( F \right) = gen\left\{ {\left( {1,0} \right),\left( {1,0} \right),\left( {0, – 1} \right)} \right\}{\rm{\;\;}} \Rightarrow {B_{Im\left( F \right)}} = \left\{ {\left( {1,0} \right),\left( {0, – 1} \right)} \right\} \Rightarrow \dim \left( {Im\left( F \right)} \right) = 2\] Entonces la imagen es \({\mathbb{R}^2}\), y la transformación es un epimorfismo (sobreyectiva). Apliquemos el teorema de las dimensiones para conocer la dimensión del núcleo: \[\dim \left( {Nu\left( F \right)} \right) = \dim \left( {{\mathbb{R}^{2 \times 2}}} \right) – \dim \left( {Im\left( F \right)} \right) = 4 – 2 = 2\] Entonces no es un monomorfismo. Conclusión: \(F\) es un epimorfismo.
Ejemplo 3
Consideremos la siguiente transformación lineal \[G:{\mathbb{R}^2} \to {P_1}{\rm{\;\;\;}},{\rm{\;\;\;\;}}G\left( {\left( {a,b} \right)} \right) = 2a – bx\] Busquemos su núcleo: \[2a – bx = 0 + 0.x{\rm{\;}} \Rightarrow a = 0{\rm{\;}} \wedge {\rm{\;}}b = 0 \Rightarrow Nu\left( G \right) = \left\{ {\left( {0,0} \right)} \right\} \Rightarrow \dim \left( {Nu\left( F \right)} \right) = 0\] Por la propiedad enunciada anteriormente, podemos afirmar que \(G\) es un monomorfismo. Veamos cuál es la imagen: \[2a.\left( 1 \right) + b.\left( { – x} \right){\rm{\;}} \Rightarrow Im\left( G \right) = gen\left\{ {1, – x} \right\} \Rightarrow \dim \left( {Im\left( G \right)} \right) = 2\] Por lo tanto la imagen es \({P_1}\) y la transformación es un epimorfismo (sobreyectiva). Como es monomorfismo y epimorfismo, entonces es un isomorfismo.
Ejemplo 4
¿Habrá alguna TL que no sea ni monomorfismo, ni epimorfismo? ¿Que no sea ni inyectiva ni sobreyectiva? Consideremos la siguiente TL que analizamos en el ejemplo 2 de «Imagen de una TL»: \[F:{\mathbb{R}^3} \to {\mathbb{R}^{2 \times 2}}{\rm{\;\;\;\;\;}},{\rm{\;\;\;\;}}F\left( {\left( {x,y,z} \right)} \right) = \left( {\begin{array}{*{20}{c}}{x + y}&{x – z}\\0&{y + z}\end{array}} \right)\] Vimos que \({B_{Nu}} = \left\{ {\left( {1, – 1,1} \right)} \right\}\), así que no es un monomorfismo. Vimos que \({B_{Im}} = \left\{ {\left( {\begin{array}{*{20}{c}}1&1\\0&0\end{array}} \right),\left( {\begin{array}{*{20}{c}}1&0\\0&1\end{array}} \right)} \right\}\), así que no es un epimorfismo. Conclusión: existen TL que no son ni monomorfismos ni epimorfismos.
Propiedad
Sea \(F:\;V \to W\) una TL., \(\;dim\left( V \right) = \;dim\left( W \right) = \;n\)
Puede afirmarse que: \(F\) es inyectiva \( \Leftrightarrow \) \(F\) es sobreyectiva \( \Leftrightarrow \) \(F\) es biyectiva.
Sugerimos al lector demostrar esta propiedad, teniendo en cuenta que:
\(F\) es inyectiva \( \Leftrightarrow \) \(Nu\left( F \right) = \left\{ {{0_V}} \right\}{\rm{\;}}\) \( \Leftrightarrow {\rm{\;\;}}dim\left( {Nu} \right){\rm{\;}} = {\rm{\;}}0\)
Ejemplo
Dada la TL \(T:{\mathbb{R}^3} \to {\mathbb{R}^3}\), \(T\left( {x,y,z} \right) = \left( {x + y + z\;,\;\;2y\; + \;z,\;\;3y\; + \;kz} \right)\) , encontrar todos los valores de \(k\) para los cuales \(T\) es biyectiva (isomorfismo).
Resolución
Como la TL va de \({\mathbb{R}^3}\) a \({\mathbb{R}^3}\), es suficiente analizar para qué valores de k es inyectiva (o sobreyectiva).
Por inyectividad:
Si pensamos en la inyectividad, tenemos que buscar que el núcleo sea \(\left\{ {\left( {0,0,0} \right)} \right\}\). Es decir que el sistema \[\left\{ {\begin{array}{*{20}{c}}{x + y + z = 0}\\{2y + z = 0}\\{3y + kz = 0}\end{array}} \right.\] tiene que ser compatible determinado. Hemos visto que un sistema de ecuaciones \(A.X = b\) es compatible determinado \( \Leftrightarrow \) \(\det \left( A \right) \ne 0\), así que planteamos esta condición para hallar los valores de \(k\): \[\left| {\begin{array}{*{20}{c}}1&1&1\\0&2&1\\0&3&k\end{array}} \right| = 1.\left( {2k – 3} \right) \ne 0 \Rightarrow k \ne \frac{3}{2}\] Luego \(\;\forall k \in \mathbb{R},\;\;k \ne \frac{3}{2}\;\;\) la transformación lineal \(T\) es biyectiva. Por sobreyectividad Si pensamos en la sobreyectividad, tenemos que buscar que la dimensión de la imagen sea 3 (o sea que la imagen sea \({\mathbb{R}^3}\)). Recordemos que los transformados de una base del dominio generan la imagen: \[T\left( {1,0,0} \right){\rm{\;}} = \left( {1,0,0} \right)\] \[T\left( {0,1,0} \right){\rm{\;}} = \left( {1,2,3} \right)\] \[T\left( {0,0,1} \right){\rm{\;}} = \left( {1,1,k} \right)\] Como queremos que sea sobreyectiva, los tres vectores que se obtuvieron deben generar todo \({\mathbb{R}^3}\), así que deben ser LI. Recordemos que: \[det\left( A \right) \ne 0 \Leftrightarrow rango\left( A \right) = n \Leftrightarrow las\;filas\;\left( {columnas} \right)de\;A\;son\;LI\] Apliquemos esta propiedad: \[\left| {\begin{array}{*{20}{c}}1&0&0\\1&2&3\\1&1&k\end{array}} \right| = 2k – 3 \ne 0 \Rightarrow k \ne \frac{3}{2}\] Así que hemos llegado a la misma conclusión: si \(k \ne \frac{3}{2}\) la transformación lineal \(T\) es biyectiva. Resumiendo: no es necesario analizar inyectividad y sobreyectividad separadamente, ya que una de ellas implica la otra y por lo tanto, que se cumpla una de ellas implica que la transformación lineal es biyectiva. Esto sólo ocurre cuando el dominio y el codominio tienen la misma dimensión.
Para pensar:
Si las dimensiones del dominio y del codominio son distintas, ¿la TL puede ser biyectiva? Para responder, les sugerimos que consideren dos casos:
i) \(dim\left( V \right) > dim\left( W \right)\)
ii) \(dim\left( V \right) < dim\left( W \right)\)
Ejercio para el lector 1
Dada la transformación lineal \(T:{\mathbb{R}^3} \to {\mathbb{R}^3}\), \(T\left( {x,y,z} \right)\; = \;\left( {x + y + z,\;x + ky – z,\;3y – kz} \right)\) Hallar en cada caso los valores de \(k\) para los cuales: a) \(T\) es biyectiva. b) \(T\) no es biyectiva y \(\left( {0,1, – 1} \right)\) pertenece a la imagen de \(T\).

