Queremos construir una matriz que nos permita cambiar las coordenadas de un vector en una base por las coordenadas del mismo vector en otra base. Consideremos en un espacio vectorial \(V\) la función identidad, que transforma cada vector en sí mismo. Dejamos a cargo del lector demostrar que es una T.L. \[Id:V \to V{\rm{\;}}|{\rm{\;}}Id\left( v \right) = v\]
Observación: Si \(V\; = \mathbb{R}\), la función identidad es \(f\left( x \right) = x\). Tomemos un par de bases del mismo espacio vectorial \(V\): \[B = \left\{ {{v_1}, \ldots ,{v_n}} \right\}\] \[B{\rm{‘}} = \left\{ {{w_1}, \ldots ,{w_n}} \right\}\] Construyamos ahora la matriz asociada a la transformación lineal identidad: \[M{\left( {Id} \right)_{BB{\rm{‘}}}} = \left( {{{\left[ {{v_1}} \right]}_{B’}},{\rm{\;}} \ldots ,{\rm{\;}}{{\left[ {{v_n}} \right]}_{B’}}} \right) \in {\mathbb{R}^{n \times n}}\] Recordemos que: \[M{\left( F \right)_{BB{\rm{‘}}}}{\rm{\;}}{\left[ v \right]_B} = {\left[ {F\left( v \right)} \right]_{B{\rm{‘}}}}\] En el caso particular de la transformación identidad, teniendo en cuenta que \(Id\left( v \right) = v\), resulta: \[M{\left( {Id} \right)_{BB’}}.{\left[ v \right]_B} = {\left[ v \right]_{B’}}\] ¿Qué efecto produce esta matriz? Cambia las coordenadas, o sea el sistema de referencia. No transforma el vector pues \(Id\left( v \right) = v\).
\(M{\left( {Id} \right)_{BB’}}\) se denomina matriz de cambio de base de \(B\) a \(B’\).
¿Qué rango tiene esta matriz? Tiene rango \(n\) ya que sus columnas son LI por ser coordenadas de vectores de una base de \(V\).
Por ser \(M{\left( {Id} \right)_{BB’}} \in {\mathbb{R}^{n \times n}}\) de rango \(n\), es inversible.
¿Qué efecto produce la matriz inversa? Nos permite volver a la primera base, como lo indica el siguiente esquema:
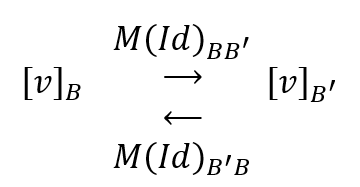
Si \(P\; = \;M{\left( {Id} \right)_{BB’}}\) entonces \({P^{ – 1}}\; = \;M{\left( {Id} \right)_{B’B}}\).
Ejemplo 1
Consideremos las siguientes bases de \({\mathbb{R}^2}\): \[{B_1} = \left\{ {\left( {1,0} \right),\;\left( {1,3} \right)} \right\}\] \[{B_2} = \left\{ {\left( {0,1} \right),\left( {1,1} \right)} \right\}\] \[E = \left\{ {\left( {1,0} \right),\left( {0,1} \right)} \right\}\]
a) Hallar \(M{\left( {Id} \right)_{{B_1}{B_2}}}\)
b) Hallar \(M{\left( {Id} \right)_{{B_1}E}}\)
c) Hallar \(M{\left( {Id} \right)_{E{B_1}}}\)
Resolución
Ítem a
Se construye la matriz de cambio de base buscando las coordenadas en la base \({B_2}\) de los vectores de la base \({B_1}\).
\[M{\left( {Id} \right)_{{B_1}{B_2}}} = \left( {{{\left[ {{v_1}} \right]}_{{B_2}}}\;\;\;\;{{\left[ {{v_2}} \right]}_{{B_2}}}} \right)\]
Busquemos las coordenadas de \(\left( {1,0} \right)\) en la base \({B_2}\):
\[\left( {1,0} \right) = \alpha .\left( {0,1} \right) + \beta .\left( {1,1} \right)\] \[ \Rightarrow \alpha = \; – 1\;\; \wedge \beta = 1\] \[ \Rightarrow {\left[ {\left( {1,0} \right)} \right]_{{B_2}}} = \left( {\begin{array}{*{20}{c}}{ – 1}\\1\end{array}} \right)\] Busquemos las coordenadas de \(\left( {1,3} \right)\) en la base \({B_2}\): \[\left( {1,3} \right) = \alpha .\left( {0,1} \right) + \beta .\left( {1,1} \right)\] \[ \Rightarrow \alpha = 2\;\; \wedge \;\beta = 1\] \[ \Rightarrow {\left[ {\left( {1,3} \right)} \right]_{{B_2}}} = \left( {\begin{array}{*{20}{c}}2\\1\end{array}} \right)\] \[M{\left( {Id} \right)_{{B_1}{B_2}}} = \left( {\begin{array}{*{20}{c}}{ – 1}&2\\1&1\end{array}} \right)\]
Ítem b
Se construye la matriz de cambio de base buscando las coordenadas en la base \(E\) de los vectores de la base \({B_1}\). \[M{\left( {Id} \right)_{{B_1}E}} = \left( {{{\left[ {{v_1}} \right]}_E}\;\;\;\;{{\left[ {{v_2}} \right]}_E}} \right)\] Pero las coordenadas en base canónicas son las mismas componentes del vector. Podemos verificarlo para \(\left( {1,0} \right)\): \[\left( {1,0} \right) = \alpha \left( {1,0} \right) + \beta \left( {0,1} \right) \Rightarrow \alpha = 1,\;\beta = 0\] Entonces las coordenadas de \(\left( {1,0} \right)\) en la base canónica son justamente \(\left( {\begin{array}{*{20}{c}}1\\0\end{array}} \right)\): \[{\left[ {\left( {1,0} \right)} \right]_E} = \left( {\begin{array}{*{20}{c}}1\\0\end{array}} \right)\] Para el vector \(\left( {1,3} \right)\) podemos escribir: \[{\left[ {\left( {1,3} \right)} \right]_E} = \left( {\begin{array}{*{20}{c}}1\\3\end{array}} \right)\] Así que la matriz de cambio de base resulta: \[M{\left( {Id} \right)_{{B_1}E}} = \left( {\begin{array}{*{20}{c}}1&1\\0&3\end{array}} \right)\] Que podemos decir que se construyó ubicando a los vectores de la base \({B_1} = \left\{ {\left( {1,0} \right),\left( {1,3} \right)} \right\}\) como columnas de la matriz.
Ítem c
Se pide que hallemos \(M{\left( {Id} \right)_{E{B_1}}}\), pero según hemos visto esta matriz es la inversa de \(M{\left( {Id} \right)_{{B_1}E\;}}\): \[M{\left( {Id} \right)_{E{B_1}}} = \frac{1}{3}.\left( {\begin{array}{*{20}{c}}3&{ – 1}\\0&1\end{array}} \right) = \left( {\begin{array}{*{20}{c}}1&{ – \frac{1}{3}}\\0&{\frac{1}{3}}\end{array}} \right)\]
Ejemplo 2
Sean \({B_1}\) y \({B_2}\) bases de \({\mathbb{R}^2}\) tales que \(P = \left( {\begin{array}{*{20}{c}}1&1\\0&{ – 3}\end{array}} \right)\) es la matriz de cambio de base de \({B_1}\) a \({B_2}.\)
a) Si \({\left[ u \right]_{{B_1}}} = \left( {\begin{array}{*{20}{c}}{ – 1}\\4\end{array}} \right)\) calcular \({\left[ u \right]_{{B_2}}}\)
b) Si \({\left[ v \right]_{{B_2}}} = \left( {\begin{array}{*{20}{c}}3\\5\end{array}} \right)\) calcular \({\left[ v \right]_{{B_1}}}\)
c) Si \({B_1} = \left\{ {\left( {1,3} \right),\left( {0,4} \right)} \right\}\), obtener la base \({B_2}\). ¿Es única?
Resolución
Ítem a
Según la propiedad de la matriz de cambio de base: \[P.{\left[ u \right]_{{B_1}}} = {\left[ u \right]_{{B_2}}} \Rightarrow {\rm{\;}}{\left[ u \right]_{{B_2}}} = \left( {\begin{array}{*{20}{c}}1&1\\0&{ – 3}\end{array}} \right).\left( {\begin{array}{*{20}{c}}{ – 1}\\4\end{array}} \right) = \left( {\begin{array}{*{20}{c}}3\\{ – 12}\end{array}} \right){\rm{\;}}\] ¿Podemos determinar cuál es el vector \(u\)? No, porque no tenemos información sobre las bases.
Ítem b
Ahora es en sentido contrario: \[{\left[ v \right]_{{B_2}}} = \left( {\begin{array}{*{20}{c}}3\\5\end{array}} \right) \to {\left[ v \right]_{B1{\rm{\;}}}} = ?\] \[P.{\left[ v \right]_{{B_1}}} = {\left[ v \right]_{{{\rm{B}}_2}}} \Rightarrow \left( {\begin{array}{*{20}{c}}1&1\\0&{ – 3}\end{array}} \right).{\left[ v \right]_B} = \left( {\begin{array}{*{20}{c}}3\\5\end{array}} \right){\rm{\;}} \Rightarrow {\left[ v \right]_B} = \left( {\begin{array}{*{20}{c}}{\frac{{14}}{3}}\\{ – \frac{5}{3}}\end{array}} \right){\rm{\;}}\]
Ítem c
En este punto nos dan la base \({B_1}\): \[{B_1} = \left\{ {\left( {1,3} \right),\left( {0,4} \right)} \right\}\] ¿Puede determinarse \({B_2}\)? Sabemos que: \[Id\left( {\left( {1,3} \right)} \right) = \left( {1,3} \right)\] \[Id\left( {\left( {0,4} \right)} \right) = \left( {0,4} \right)\] \[{v_1} = \left( {1,3} \right){\rm{\;\;}}{v_2} = \left( {0,4} \right)\] \[P = M{\left( {Id} \right)_{{B_1}{{\rm{B}}_2}}} = \left( {{{\left[ {{v_1}} \right]}_{{{\rm{B}}_2}}}{\rm{\;\;\;\;}}{{\left[ {{v_2}} \right]}_{{{\rm{B}}_2}}}} \right) = \left( {\begin{array}{*{20}{c}}1&1\\0&{ – 3}\end{array}} \right)\] Queremos obtener: \[{B_2} = \left\{ {{w_{1{\rm{\;}}}},{\rm{\;}}{w_2}} \right\}\] \[\left( {1,3} \right) = 1.{w_1} + 0.{w_2} \Rightarrow {w_1} = \left( {1,3} \right)\] \[\left( {0,4} \right) = 1.{w_1} + \left( { – 3} \right).{w_2} \Rightarrow {w_2} = \frac{{\left( {0,4} \right) – \left( {1,3} \right)}}{{ – 3}} = \left( {\frac{1}{3}, – \frac{1}{3}} \right)\] Quiere decir que si tenemos como dato la matriz de cambio de base, podemos determinar la base \({B_2}\;\)a partir de la base \({B_1}\) y viceversa.
Cómo afecta un cambio de base a la matriz asociada a una TL
En este apartado nos interesa estudiar cuál es la relación entre dos matrices asociadas a una misma transformación lineal, pero que están expresadas en bases diferentes.
Sean:
- \(T:V \to W\) una transformación lineal
- \({B_1},{B_3}\) bases de \(V\)
- \({B_2},{B_4}\) bases de \(W\)
- \(I{d_V}\) la transformación lineal identidad en el espacio vectorial \(V\)
- \(I{d_W}\) la transformación lineal identidad en el espacio vectorial \(W\)
¿Qué relación existe entre \(M{\left( T \right)_{{B_1}{B_2}}}\) y \(M{\left( T \right)_{{B_3}{B_4}}}\;\)? ¿Cómo se podría a partir de una de ellas calcular la otra? Por las propiedades de las matrices asociadas a una TL, puede afirmarse que: \[M{\left( T \right)_{{B_1}{B_2}}}{\left[ v \right]_{{B_1}}} = {\left[ {T\left( v \right)} \right]_{{B_2}}}\] \[M{\left( T \right)_{{B_3}{B_4}}}{\left[ v \right]_{{B_3}}} = {\left[ {T\left( v \right)} \right]_{{B_4}}}\] \[M{\left( {I{d_V}} \right)_{{B_3}{B_1}}}{\left[ v \right]_{{B_3}}} = {\left[ v \right]_{{B_1}}}\] \[M{\left( {I{d_W}} \right)_{{B_2}{B_4}}}{\left[ {T\left( v \right)} \right]_{{B_2}}} = {\left[ {T\left( v \right)} \right]_{{B_4}}}\] Si el lector leyó cuidadosamente las igualdades anteriores, estará convencido de que son válidas (si no está convencido, sugerimos consultar por el foro). Las relaciones enunciadas pueden verse convenientemente en el siguiente esquema:
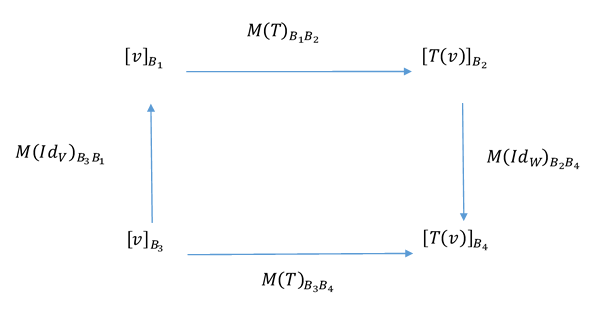
De todo esto es posible deducir que: \[M{\left( T \right)_{{B_3}{B_4}}} = M{\left( {I{d_W}} \right)_{{B_2}{B_4}}}.M{\left( T \right)_{{B_1}{B_2}}}.M{\left( {I{d_V}} \right)_{{B_3}{B_1}}}\]
Caso particular de \({\mathbb{R}^n}\) a \({\mathbb{R}^n}\)
Nos interesa especialmente el caso de las TL \(T:\;{\mathbb{R}^n} \to {\mathbb{R}^n}\), y la relación entre la matriz estándar y otra matriz asociada \(M{\left( T \right)_{BB}}\) , con \(B\) base de \({\mathbb{R}^n}\). Volvamos a construir el esquema para este caso particular: 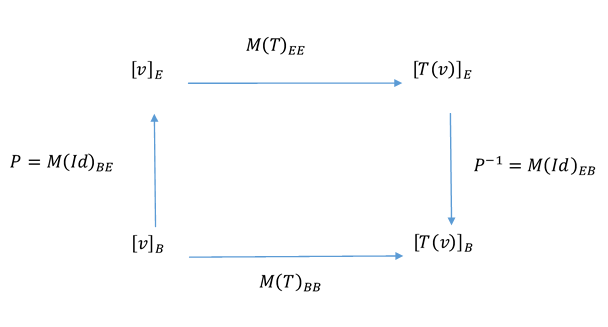 Habíamos visto que: \[M{\left( T \right)_{{B_3}{B_4}}} = M{\left( {Id} \right)_{{B_2}{B_4}}}.M{\left( T \right)_{{B_1}{B_2}}}.M{\left( {Id} \right)_{{B_3}{B_1}}}\] En este caso particular la expresión queda: \[ \Rightarrow M{\left( T \right)_{BB}} = M{\left( {Id} \right)_{EB}}.M{\left( T \right)_{EE}}.M{\left( {Id} \right)_{BE}}\] Por lo tanto: \[M{\left( T \right)_{BB}} = {P^{ – 1}}M{\left( T \right)_{EE}}\;P\;\;\;\;\;\;\;\;\;\;\;{\rm{\;donde\;\;\;\;\;\;\;}}P = M{\left( {Id} \right)_{BE}}\]
Habíamos visto que: \[M{\left( T \right)_{{B_3}{B_4}}} = M{\left( {Id} \right)_{{B_2}{B_4}}}.M{\left( T \right)_{{B_1}{B_2}}}.M{\left( {Id} \right)_{{B_3}{B_1}}}\] En este caso particular la expresión queda: \[ \Rightarrow M{\left( T \right)_{BB}} = M{\left( {Id} \right)_{EB}}.M{\left( T \right)_{EE}}.M{\left( {Id} \right)_{BE}}\] Por lo tanto: \[M{\left( T \right)_{BB}} = {P^{ – 1}}M{\left( T \right)_{EE}}\;P\;\;\;\;\;\;\;\;\;\;\;{\rm{\;donde\;\;\;\;\;\;\;}}P = M{\left( {Id} \right)_{BE}}\]
Ejemplo
\[T{\mathbb{R}^2} \to {\mathbb{R}^2}\] \[M{\left( T \right)_{EE}} = \left( {\begin{array}{*{20}{c}}1&3\\2&2\end{array}} \right)\] \[B = \left\{ {\left( {1,1,} \right),\left( {3, – 2} \right)} \right\}\] Queremos encontrar \(M{\left( T \right)_{BB}}\) . Calculamos la matriz de cambio de base: \[P = M{\left( {Id} \right)_{BE}} = \left( {\begin{array}{*{20}{c}}1&3\\1&{ – 2}\end{array}} \right)\] Buscamos su inversa: \[{P^{ – 1}} = M{\left( {Id} \right)_{EB}} = – \frac{1}{5}\left( {\begin{array}{*{20}{c}}{ – 2}&{ – 3}\\{ – 1}&1\end{array}} \right)\] Entonces resulta: \[M{\left( T \right)_{BB}} = {P^{ – 1}}.M{\left( T \right)_{EE}}.P = \left( {\begin{array}{*{20}{c}}4&0\\0&{ – 1}\end{array}} \right)\] Observemos que en esta base \(B\), la matriz asociada es diagonal. Dada una TL en \({\mathbb{R}^n}\), ¿cuándo es posible hallar una base \(B\) de modo que la matriz asociada en esa base resulte diagonal? La respuesta la encontraremos en la próxima unidad.
Ejercicio para el lector 6
a) Eligiendo una base adecuada, definir una transformación lineal \(T:{\mathbb{R}^3} \to {\mathbb{R}^3}\) que represente la simetría (reflexión) respecto del plano \(\pi :\;\;x – z = 0\) .
b) Hallar si es posible, una base \(B\) de \({\mathbb{R}^3}\) de modo que la matriz asociada a \(T\) sea: \[M{\left( T \right)_{BB}} = \left( {\begin{array}{*{20}{c}}1&0&0\\0&1&0\\0&0&{ – 1}\end{array}} \right)\] Sugerencia: si \(B = \left\{ {{v_1},{v_2},{v_3}} \right\}\), ¿cuáles son los transformados de los vectores de \(B\)? (Tener en cuenta cómo se construye \(M{\left( T \right)_{BB}}\)).
c) Obtener la matriz de \(T\) respecto de la base canónica de \({\mathbb{R}^3}\).

