Ángulo entre dos planos
Sean los planos \({\pi _1}\;:\;\;{a_1}x\; + \;{b_1}y\; + \;{c_1}z\; + \;{d_1}\; = \;0\) y \({\pi _2}\;:\;\;{a_2}x\; + \;{b_2}y\; + \;{c_2}z\; + \;{d_2}\; = \;0\).
Dichos planos forman dos ángulos suplementarios, como muestra la figura:
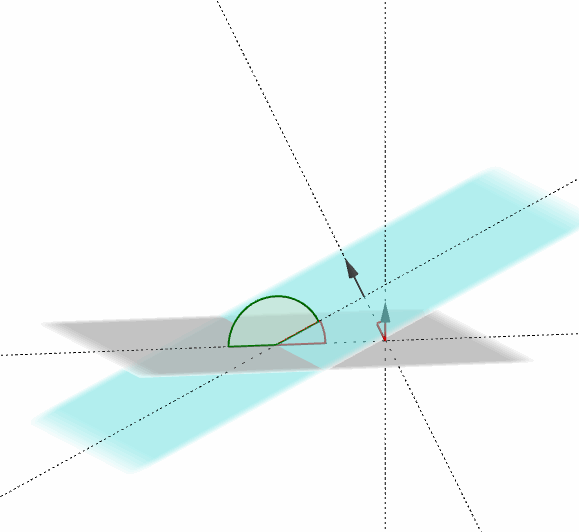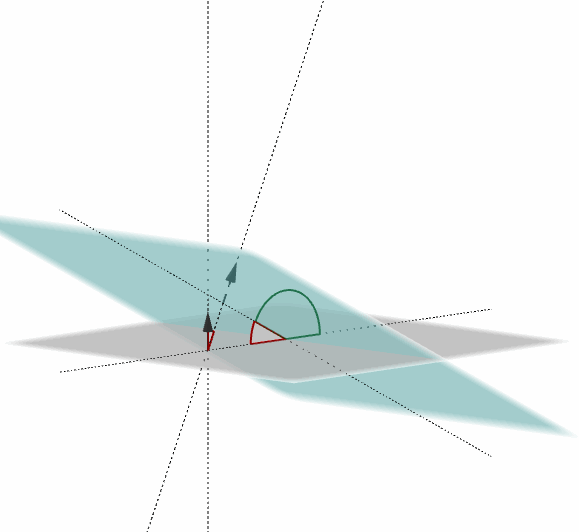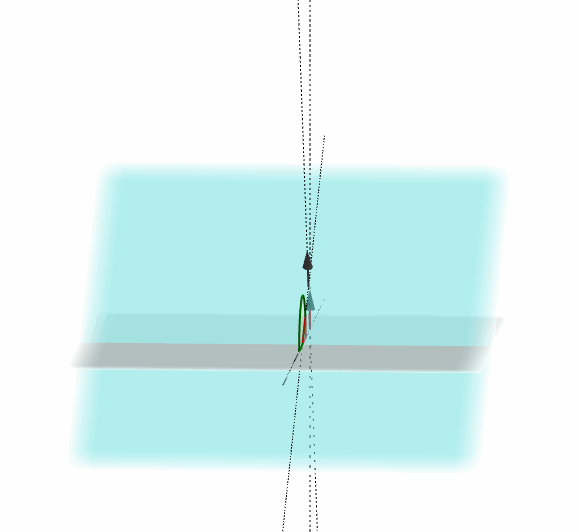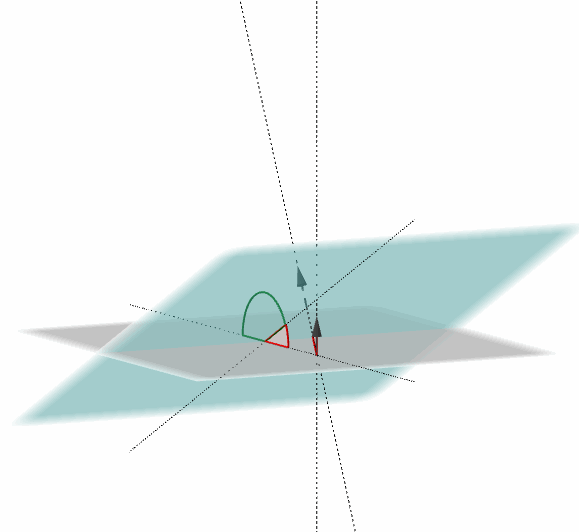
El ángulo entre dos planos es el ángulo entre sus respectivos vectores normales:
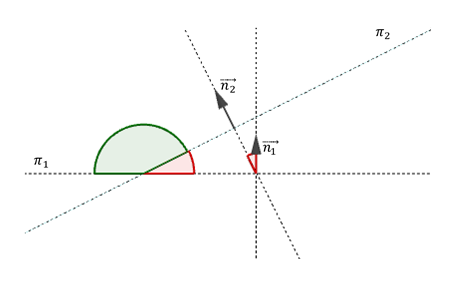
\[á ng\left( {{\pi _1},{\pi _2}} \right) = á ng\left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)\]
Si llamamos \(\theta \;\) a dicho ángulo, resulta:
\[\cos \left( \theta \right) = \frac{{\overrightarrow {{n_1}} .\overrightarrow {{n_2}} }}{{\lVert\overrightarrow {{n_1}}\rVert \lVert\overrightarrow {{n_2}}\lVert }}\]
Según el sentido de \(\overrightarrow {{n_1}} \;\;y\;\;\overrightarrow {{n_2}} \) , se obtendrá alguno de los dos ángulos suplementarios. Convenimos en tomar el menor de estos ángulos, por lo cual agregamos módulo en la fórmula anterior:
\[\cos \left( \theta \right) = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\lVert\overrightarrow {{n_1}}\rVert \lVert\overrightarrow {{n_2}}\rVert }}\]
Ejemplo
Dados los planos:
\[{\pi _1}:\;\;\;x – y + 2 = 0\]
\[{\pi _2}:\left( {x,y,z} \right) = \alpha \left( {1,2,3} \right) + \beta \left( {0,1,1} \right)\;\]
Calcular \(á ng\left( {{\pi _1},{\pi _2}} \right)\).
El plano \({\pi _2}\) está dado en forma vectorial paramétrica, para hallar el ángulo pedido necesitamos \(\overrightarrow {{n_2}} \;\):
\[\overrightarrow {{n_2}} = \left( {1,2,3} \right) \times \left( {0,1,1} \right) = \left( { – 1, – 1,1} \right)\]
\[\overrightarrow {{n_1}} = \left( {1, – 1,0} \right)\;\]
\[\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 0\]
Esto quiere decir que \(\overrightarrow {{n_1}} \bot \overrightarrow {{n_2}} \), entonces el ángulo es \(\theta = 90^\circ \).
La definición de ángulo entre planos nos permite enunciar condiciones de perpendicularidad y de paralelismo entre planos.
Planos perpendiculares y planos paralelos
Sean \({\pi _1}\) y \({\pi _2}\) planos de vectores normales \(\overrightarrow {{n_1}} \) y \(\overrightarrow {{n_2}} \) respectivamente:
\[Planos\;perpendiculares:\;\;\;\;\;{\pi _1} \bot {\pi _2}\;\; \Leftrightarrow \;\;\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 0\]
\[Planos\;paralelos:\;\;\;{\pi _1}\parallel {\pi _2}\;\; \Leftrightarrow \;\;\overrightarrow {{n_1}} \parallel \overrightarrow {{n_2}} \;\; \Leftrightarrow \;\;\overrightarrow {{n_1}} = k\overrightarrow {{n_2}} \;\;\;,\;k \in R\]
Consideremos por ejemplo:
\[{\pi _1}:\;\;2x – 3y + z + 1 = 0\;\;\;\;\;\;\;\;\;\;\overrightarrow {\;{n_1}} = \left( {2, – 3,1} \right)\]
\[{\pi _2}:\;\;4x – 6y + 2z + 5 = 0\;\;\;\;\;\;\;\;\;\;\;\overrightarrow {{n_2}} = \left( {4, – 6,2} \right)\]
\[{\pi _3}:\;\;4x – 6y + 2z + 2 = 0\;\;\;\;\;\;\;\;\;\;\;\overrightarrow {{n_3}} = \left( {4, – 6,2} \right)\]
Como \({n_2}\; = 2\;{n_1}\) , podemos afirmar que \({\pi _1}\) y \({\pi _2}\) son paralelos.
Análogamente, como \({n_3}\; = \;2\;{n_1}\) , los planos \({\pi _1}\) y \({\pi _3}\) también son paralelos. Pero además se verifica que \({d_3}\; = \;2\;{d_1}\), por lo cual \({\pi _1}\) y \({\pi _3}\) son coincidentes, o sea \({\pi _1} = {\pi _3}\).
Distancia de un punto a un plano
Dados un plano \(\pi :\;\;ax + by + cz + d = 0\) y un punto \(A\left( {{x_A},{y_A},{z_A}} \right)\) , nos proponemos calcular la distancia de \(A\) a \(\pi \).
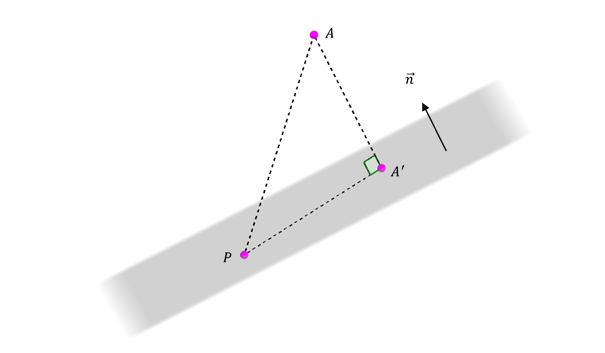
La distancia de \(A\) a \(\pi \) es la longitud del segmento , siendo la proyección ortogonal (perpendicular) de \(A\) sobre \(\pi \).
Consideremos un punto cualquiera \(P\left( {x,y,z} \right)\) perteneciente a \({\rm{\pi }}\).
\[\overrightarrow {A’A} = {\overrightarrow {proy} _{\vec n}}\left( {\overrightarrow {PA} } \right)\]
Entonces
\(dist\left( {A,\pi } \right) = \lVert{\overrightarrow {proy} _{\vec n}}\left( {\overrightarrow {PA} } \right) \rVert \) siendo \(P\) un punto cualquiera del plano
Veamos un ejemplo, dados:
\[\pi :\;\;x + 2y + 3z + 1 = 0\]
\[A\left( {0,2,1} \right)\]
Calcular \(dist\left( {A,\pi } \right)\)
Recordemos que la norma de la proyección de un vector en la dirección de otro se calcula así:
\[\lVert{\overrightarrow {proy} _{\vec n}}\left( {\overrightarrow {PA} } \right) \rVert = \frac{{\left| {\overrightarrow {PA} .\vec n} \right|}}{{\lVert\vec n\rVert}}\]
Tomemos un punto cualquiera del plano, por ejemplo \(P\left( { – 1,0,0} \right).\;\)Entonces
\[\overrightarrow {PA} = \left( {1,2,1} \right)\]
\[dist\left( {A,\pi } \right) = \lVert {\overrightarrow {proy} _{\vec n}}\left( {\overrightarrow {PA} } \right)\rVert = \frac{{\left| {\overrightarrow {PA} .\vec n} \right|}}{{\lVert\vec n\rVert}} = \frac{{\left| {\left( {1,2,1} \right).\left( {1,2,3} \right)} \right|}}{{\sqrt {{1^2} + {2^2} + {3^2}} }} = \frac{8}{{\sqrt {14} }}\]
A continuación deduciremos una fórmula que permite calcular en forma muy sencilla la distancia de un punto a un plano.
Sean:
\[\pi :\;\;ax + by + cz + d = 0\]
\[A\left( {{x_A},{y_A},{z_A}} \right)\]
Habíamos visto que:
\[d\left( {A,\pi } \right) = \lVert{\overrightarrow {proy} _{\vec n}}\left( {\overrightarrow {PA} } \right)\rVert\;\;\;\;\;\;siendo\;P\left( {x,y,z} \right) \in \pi \]
\[\overrightarrow {PA} = \left( {{x_A} – x,{y_A} – y,{z_A} – z} \right)\]
\[\vec n = \left( {a,b,c} \right)\]
Entonces:
\[\lVert{\overrightarrow {proy} _{\vec n}}\left( {\overrightarrow {PA} } \right)\rVert = \frac{{\left| {\overrightarrow {PA} .\vec n} \right|}}{{\lVert\vec n\rVert}} = \frac{{\left| {a\left( {{x_A} – x} \right) + b\left( {{y_A} – y} \right) + c\left( {{z_A} – z} \right)} \right|}}{{\lVert\vec n\rVert}}\]
\[\lVert{\overrightarrow {proy} _{\vec n}}\left( {\overrightarrow {PA} } \right) \lVert= \frac{{\left| {a{x_A} + b{y_A} + c{z_A} + d} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\]
Concluimos que:
Retomemos el ejemplo que habíamos desarrollado:
\[\pi :\;\;x + 2y + 3z + 1 = 0\]
\[A\left( {0,2,1} \right)\]
De acuerdo con la fórmula demostrada, la distancia es:
\[dist\left( {A,\pi } \right) = \frac{{\left| {\;0 + 4 + 3 + 1} \right|}}{{\sqrt {{1^2} + {2^2} + {3^2}} }} = \;\frac{8}{{\sqrt {14} }}\]
Tal como habíamos calculado antes pero… ¡más fácil!
Distancia entre planos paralelos
Dados dos planos \({\pi _1}\) y \({\pi _2}\;\;\;\)paralelos, ¿cómo podemos hallar la distancia entre ambos?
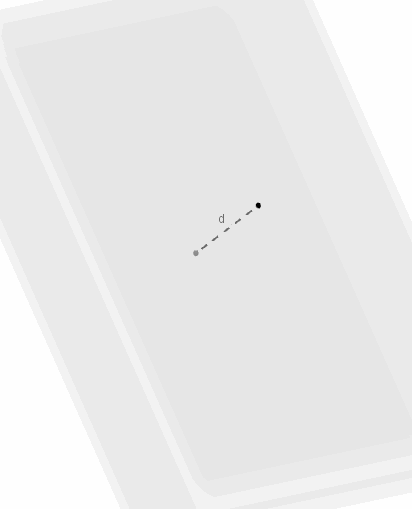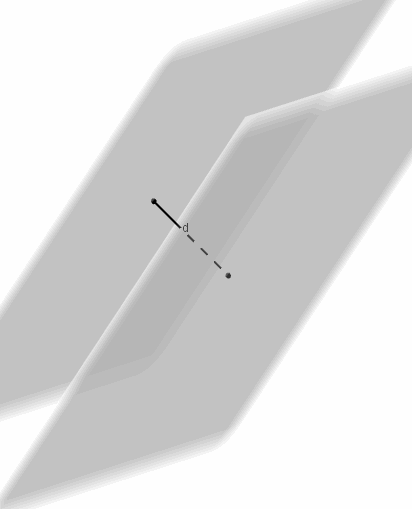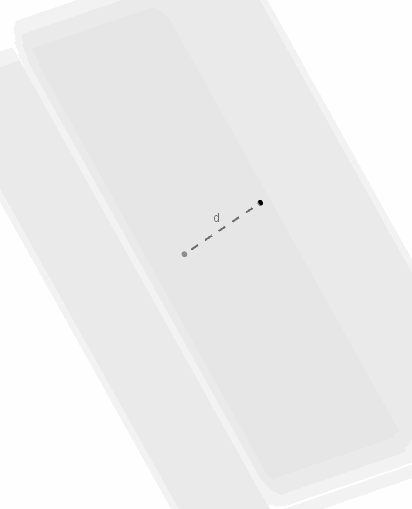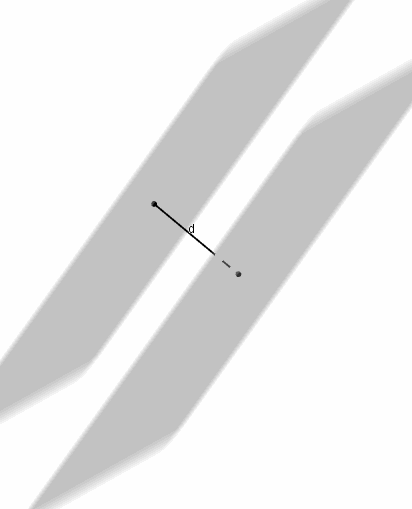
Consideremos los siguientes planos paralelos:
\({\pi _1}:\;\;2x – 3y + z + 1 = 0\;\;\;\;\;,\;\;\;\;\) \({\pi _2}:\;\;4x – 6y + 2z + 5 = 0\;\;\;\;\;\;\;\;\;\;\;\)
Todos los puntos de \({\pi _1}\) están a la misma distancia de \({\pi _2}\) , por lo tanto podemos elegir un punto cualquiera de \({\pi _1}\) y calcular su distancia a \({\pi _2}\) . Por ejemplo: \({P_1}\left( {0,0, – 1} \right)\)
Aplicamos la fórmula de distancia de un punto a un plano:
\[d\left( {{\pi _1},{\pi _2}} \right) = d\left( {{P_1},{\pi _2}} \right) = \frac{{\left| {4.0 – 6.0 + 2.\left( { – 1} \right) + 5} \right|}}{{\sqrt {{4^2} + {{\left( { – 6} \right)}^2} + {2^2}} }} = \frac{3}{{\sqrt {56} }}\]
Observación: Si los planos no son paralelos, la distancia entre ambos es 0.

