En las unidades anteriores vimos que el álgebra de vectores y el álgebra de matrices presentan similitudes. Pudimos observar que las propiedades de la suma (de vectores o de matrices) y del producto por un escalar son idénticas en ambos conjuntos. En esta unidad, generalizaremos el concepto de vector a partir de estas propiedades en común que …
Distancias y proyecciones
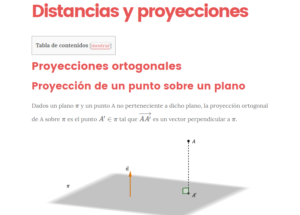
Proyecciones ortogonales Proyección de un punto sobre un plano Dados un plano \(\pi \) y un punto A no perteneciente a dicho plano, la proyección ortogonal de A sobre \(\pi \) es el punto \(A' \in \pi \) tal que \(\overrightarrow {AA'} \) es un vector perpendicular a \(\pi \). \[A' = pro{y_\pi }\left( A \right)\;\;\;si\;y\;só …
Recta en R3
Ecuaciones de la recta en R3 Sabemos que una recta en \({\mathbb{R}^2}\) puede expresarse por la ecuación: \[y = ax + b\] Pero ¿qué representa esta ecuación en \({\mathbb{R}^3}\)? En \({\mathbb{R}^3}\) es un plano paralelo al eje \(z\), y en \({\mathbb{R}^2}\) es una recta: Para definir un plano es suficiente conocer un vector …