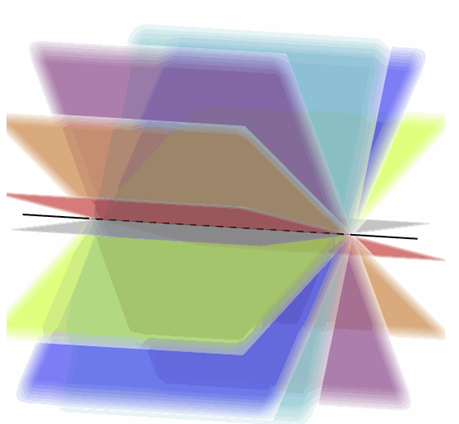
Sean \({\pi _1}\) y \({\pi _2}\) dos planos no paralelos: \[{\pi _1}:\;\;{a_1}\;x + {b_1}\;y + {c_1}\;z + {d_1} = 0\] \[{\pi _2}:\;\;{a_2}\;x + {b_{2\;}}y + {c_2}\;z + {d_2} = 0\] La intersección de dos planos no paralelos es una recta. Se denomina haz de planos al conjunto de planos que pasan por dicha recta. Uno podría imaginarse al haz …
Ángulos y distancias
Ángulo entre dos planos Sean los planos \({\pi _1}\;:\;\;{a_1}x\; + \;{b_1}y\; + \;{c_1}z\; + \;{d_1}\; = \;0\) y \({\pi _2}\;:\;\;{a_2}x\; + \;{b_2}y\; + \;{c_2}z\; + \;{d_2}\; = \;0\). Dichos planos forman dos ángulos suplementarios, como muestra la figura: …
Matrices y sistemas de ecuaciones lineales
Introducción Habíamos visto que una recta en \({\mathbb{R}^3}\) puede definirse a través de un sistema de 2 ecuaciones lineales con 3 incógnitas. Por ejemplo: \[r:\;\left\{ {\begin{array}{*{20}{c}}{x + z = 1}\\{x - y - z = 3}\end{array}} \right.\] Este sistema puede expresarse de un modo sencillo como un producto de matrices, como …
[Leer más...] acerca deMatrices y sistemas de ecuaciones lineales