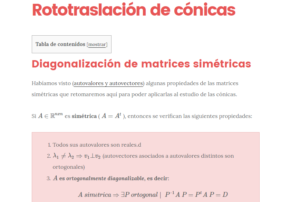
Diagonalización de matrices simétricas Habíamos visto (en autovalores y autovectores) algunas propiedades de las matrices simétricas que retomaremos aquí para poder aplicarlas al estudio de las cónicas. Si \(A \in {\mathbb{R}^{nxn}}\) es simétrica ( \(A = {A^t}\) ), entonces se verifican las siguientes propiedades: Todos sus autovalores …
Potencias de una matriz diagonalizable
Sea \(A \in {\mathbb{R}^{n \times n}}\) diagonalizable. Es decir, existe \(P \in {\mathbb{R}^{n \times n}}\) inversible tal que: \[{P^{ - 1}}AP = D\] donde \(D\) es una matriz diagonal. Recordemos que: \[A\;es\;diagonalizable\; \Leftrightarrow \;A\;tiene\;n\;autovectores\;LI\;en\;{\mathbb{R}^n}\] En la diagonal \(D\) que se obtiene están los …
[Leer más...] acerca dePotencias de una matriz diagonalizable
Ecuaciones paramétricas de las cónicas (circunferencia, elipse, parábola e hipérbola)
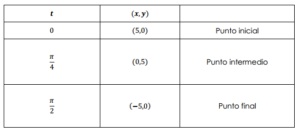
Ecuaciones paramétricas de una recta en \({\mathbb{R}^2}\) Nosotros ya vimos cómo parametrizar rectas en \({\mathbb{R}^2}\) y en \({\mathbb{R}^3}\): Un ejemplo de parametrización de una recta sería: \[\left\{ {\begin{array}{*{20}{c}}{x = 2t}\\{y = t - 1}\end{array}\;\;\forall t \in \mathbb{R}} \right.\] \[t = \frac{x}{2}\] \[y = …