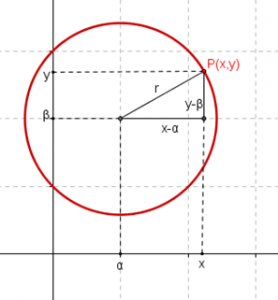
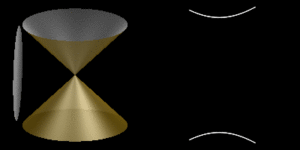Todos conocen las circunferencias, saben que pueden trazarse con un compás. Les resultará natural la siguiente definición: La circunferencia es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. \[Centro:C\left( {\alpha ,\beta } \right)\] \[\mathcal{C} = \left\{ {P\left( {x,y} \right){\rm{|}}d\left( {P,C} …
Introducción a cónicas
Definición de lugar geométrico Dada una ecuación \(F\left( {x,y} \right) = 0\) se denomina lugar geométrico al conjunto de los puntos \(P\left( {x,y} \right)\) de \({\mathbb{R}^2}\) que verifican la ecuación. Ejemplo 1 Consideremos que la ecuación \(F\left( {x,y} \right) = 0\) es: \[{x^2} - 4xy = 0\] ¿Qué tipo de lugar geométrico …
Diagonalización de una transformación lineal
Autovalores y autovectores de una transformación lineal Sea \(T:V \to V\) una transformación lineal: \(\lambda \in \mathbb{R}\) es autovalor de \(T\) si y sólo si \(\exists v \in V\) no nulo, tal que \(T\left( v \right) = \lambda .v\) \(v\) es el autovector asociado a \(\lambda \). Si \(V\) fuera un espacio de polinomios, entonces \(v\) …
[Leer más...] acerca deDiagonalización de una transformación lineal