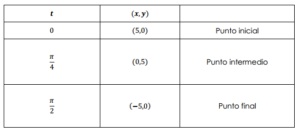
Ecuaciones paramétricas de una recta en \({\mathbb{R}^2}\) Nosotros ya vimos cómo parametrizar rectas en \({\mathbb{R}^2}\) y en \({\mathbb{R}^3}\): Un ejemplo de parametrización de una recta sería: \[\left\{ {\begin{array}{*{20}{c}}{x = 2t}\\{y = t - 1}\end{array}\;\;\forall t \in \mathbb{R}} \right.\] \[t = \frac{x}{2}\] \[y = …
Cónicas, parametrización y superficies cuádricas
Hipérbola
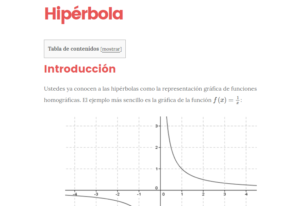
Introducción Ustedes ya conocen a las hipérbolas como la representación gráfica de funciones homográficas. El ejemplo más sencillo es la gráfica de la función \(f\left( x \right) = \frac{1}{x}\): A continuación estudiaremos las hipérbolas desde otra perspectiva. Definición de hipérbola Dados dos puntos \({F_1}\) y \({F_2}\) llamados focos, …
Elipse
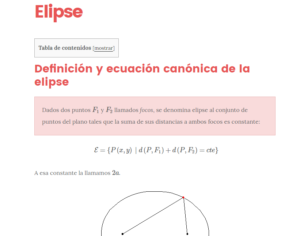
Definición y ecuación canónica de la elipse Dados dos puntos \({F_1}\) y \({F_2}\) llamados focos, se denomina elipse al conjunto de puntos del plano tales que la suma de sus distancias a ambos focos es constante: \[\mathcal{E} = \left\{ {P\left( {x,y} \right)\;|\;d\left( {P,{F_1}} \right) + d\left( {P,{F_2}} \right) = cte} \right\}\] A esa …