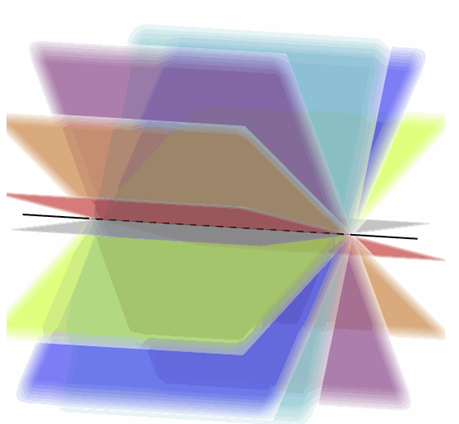
Sean \({\pi _1}\) y \({\pi _2}\) dos planos no paralelos: \[{\pi _1}:\;\;{a_1}\;x + {b_1}\;y + {c_1}\;z + {d_1} = 0\] \[{\pi _2}:\;\;{a_2}\;x + {b_{2\;}}y + {c_2}\;z + {d_2} = 0\] La intersección de dos planos no paralelos es una recta. Se denomina haz de planos al conjunto de planos que pasan por dicha recta. Uno podría imaginarse al haz …
Vectores, recta y plano.
En esta primera unidad de Álgebra y Geometría Analítica trabajaremos con vectores en R3, extendiendo al espacio tridimensional las operaciones definidas en R2 y definiendo nuevas operaciones que permitirán ampliar el campo de aplicación. Esta unidad se centra en el estudio de planos y rectas en R3.
A medida que recorran los temas desarrollados, podrán apreciar que los vectores resultan una herramienta potente para la resolución de diferentes problemas de la geometría analítica: intersecciones, distancias, ángulos, proyecciones, etc. Los conceptos trabajados en esta unidad se retomarán con frecuencia en otras unidades de la materia, proporcionando un marco geométrico que facilita la comprensión del estudio de sistemas de ecuaciones lineales, espacios vectoriales, transformaciones lineales y otros temas.

Objetivos:
-Realizar las operaciones vectoriales básicas en R3, aplicar sus propiedades y conocer su interpretación geométrica.
-Aplicar el álgebra vectorial a la resolución de una gama amplia de problemas geométricos.
-Caracterizar planos y rectas en R3 mediante sus diferentes ecuaciones y representarlos gráficamente.
-Describir haces (familias) de planos sujetos a una condición geométrica.
-Investigar posiciones relativas entre planos, entre rectas y entre planos y rectas.
-Identificar rectas coplanares y alabeadas.
-Resolver problemas de distancias, de ángulos y de proyecciones.
Ángulos y distancias
Ángulo entre dos planos Sean los planos \({\pi _1}\;:\;\;{a_1}x\; + \;{b_1}y\; + \;{c_1}z\; + \;{d_1}\; = \;0\) y \({\pi _2}\;:\;\;{a_2}x\; + \;{b_2}y\; + \;{c_2}z\; + \;{d_2}\; = \;0\). Dichos planos forman dos ángulos suplementarios, como muestra la figura: …
Ecuaciones del plano
Deducción de la ecuación general del plano Dada una dirección en \({\mathbb{R}^3}\), existen infinitos planos perpendiculares a la misma. Si conocemos además un punto del plano, éste queda determinado de forma única. Nos proponemos hallar la ecuación del plano \(\pi \) que pasa por \({P_0}\left( {{x_0},{y_0},{z_0}} \right)\) y es perpendicular …