Definición de número complejo
Un número complejo \(z\) se define como un par ordenado de números reales:
\[z = \left( {a,b} \right)\;\;\;con\;\;a,b \in \mathbb{R}\]
donde el primer elemento del par ordenado se llama parte real del número complejo, y el segundo elemento se llama parte imaginaria:
\[Re\left( z \right) = a\]
\[Im\left( z \right) = b\]
En los números complejos se definen las siguientes operaciones:
\[\left( {a,\;b} \right)\; + \;\left( {c,\;d} \right)\; = \;\left( {a\; + \;c\;,\;b\; + \;d} \right)\]
\[\left( {a,\;b} \right)\;.\;\left( {c,\;d} \right)\; = \;\left( {ac\; – \;bd\;,\;ad\; + \;bc} \right)\]
Con estas operaciones, puede demostrarse que el conjunto de los números complejos tiene las mismas propiedades que los reales con la suma y el producto. No nos extenderemos desarrollando esta cuestión algebraica porque en la práctica lo usual es operar con otras expresiones de los números complejos, como veremos a continuación.
Podemos identificar de manera natural los complejos de parte imaginaria nula con los números reales:
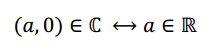
Por otra parte, los números de parte real nula: \(z = \left( {0,b} \right)\) se denominan imaginarios puros. Se define la unidad imaginaria:
Podemos entonces deducir otra forma de expresar un número complejo:
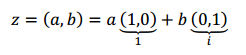
Observación: en algunos textos de Física y de Ingeniería la unidad imaginaria se designa como \(j\) , para no confundir con la \(i\) que suele indicar la intensidad de corriente eléctrica.
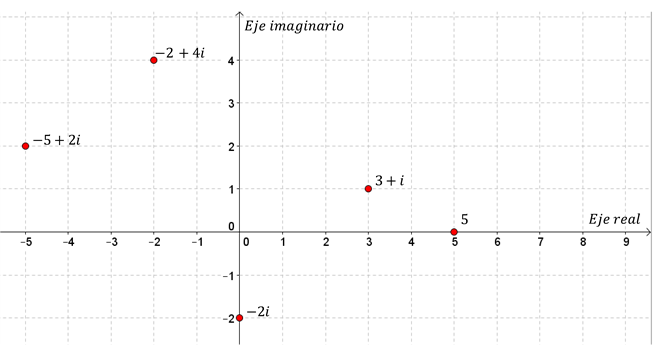
Dado que hemos definido un número complejo como un par ordenado de números reales, es natural interpretarlo como un punto del plano. En el eje de abscisas (eje real) ubicaremos los complejos de parte imaginaria nula. Y en el eje de ordenadas (eje imaginario) ubicaremos los imaginarios puros:
Operaciones en forma binómica
Suma y resta
Si \({z_1}\; = \;a + bi\) y \({z_2}\; = \;c + di\), entonces:
\[{z_1}\; + \;{z_2}\; = \;\left( {a\; + \;bi} \right)\; + \;\left( {c\; + \;di} \right)\; = \;\left( {a + c} \right)\; + \;\left( {b + d} \right)i\]
Análogamente: \({z_1}\; – \;{z_2}\; = \;\left( {a\; – \;c} \right)\; + \;\left( {b\; – \;d} \right)i\)
Multiplicación
\[{z_1}\;.\;{z_2}\; = \left( {a\; + \;bi} \right).\;\left( {c + di} \right) = \;ac\; + \;adi\; + \;bic\; + \;bd{i^2}\left[ 1 \right]\]
¿Cuánto vale \({i^2}\)?
De acuerdo con la multiplicación definida:
\[\left( {a,\;b} \right).\;\left( {c,\;d} \right) = \;\left( {ac\; – \;bd\;,\;ad\; + \;bc} \right)\left[ 2 \right]\]
Para \(i\; = \;\left( {0,\;1} \right)\) resulta:
\({i^2} = \left( {0,\;1} \right)\;.\;\left( {0,\;1} \right)\; = \;\left( { – 1,\;0} \right)\)que identificamos con el número real \(\left( { – 1} \right)\).
En resumen:
Reemplazando en \(\left[ 1 \right]\) resulta:
\[{z_1}\;.\;{z_2}\; = \left( {\;ac – bd} \right) + i\left( {ad + bc} \right)\]
Pueden verificar que es coherente con la definición \(\left[ 2 \right]\).
Conjugado de un número complejo
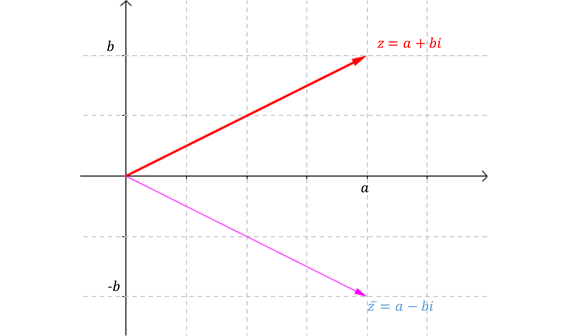
El conjugado de \(z = a + bi\) , se define así:
\[\bar z = a – bi\]
Observamos que \(z\) y \(\bar z\) son simétricos respecto del eje real, como muestra la siguiente figura:
Propiedades:
1) \(z\; + \;\bar z = a + bi + a – bi = 2a = \;2\;Re\left( z \right)\)
2) \(z\; – \;\bar z\; = a + bi – \left( {a – bi} \right) = 2bi = \;2i.Im\left( z \right)\)(recordar que \(Im\left( z \right) \in \mathbb{R}\) )
3) \(z.\bar z = \left( {a + bi} \right)\left( {a–bi} \right) = {a^2}–abi + bia–{b^2}{i^2} = \left( {{a^2} + {b^2}} \right) \in \mathbb{R} > 0\;\)para todo \(z \ne 0\)
División en complejos
Esta última propiedad nos permite calcular el cociente entre dos números complejos.
Sean \({z_1} = a + bi\) , \({z_2} = c + di\)
Para hallar\({z_1}/{z_2}\)multiplicamos el numerador y el denominador por el conjugado del denominador:
\[\frac{{{z_1}}}{{{z_2}}} = \frac{{{z_1}}}{{{z_2}}}.\frac{{\overline {{z_2}} }}{{\overline {{z_2}} }}\]
Entonces:
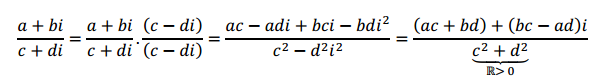
Ejemplos
Sean los números complejos:
\[{z_1} = 2 + 3i\;\;\;;\;\;\;\;{z_2} = 1 – i\;\;\;;\;\;\;\;\;{z_3} = – 3 + i\;\;\;;\;\;\;{z_4} = 1 – i\]
Calcular:

Resolución
Ítem a
\[{z_1} – 2{z_2} = \left( {2 + 3i} \right) – 2\left( {1 – i} \right) = 2 – 2 + i\left( {3 + 2} \right) = 5i\]
Ítem b
\[{z_1}.{z_3} = \;\left( {2 + 3i} \right)\left( { – 3 + i} \right) = – 6 + 2i – 9i + 3{i^2} = – 9 – 7i\]
Ítem c
\[{z_2}^2 + {z_3} = {\left( {1 – i} \right)^2} + \left( { – 3 + i} \right) = 1 – 2i + {i^2} – 3 + i = – 3 – i\]
Ítem d
\[\frac{{{z_4}}}{{{z_3}}} = \frac{{1 – i}}{{ – 3 + i}} = \frac{{1 – i}}{{ – 3 + i}}.\frac{{\left( { – 3 – i} \right)}}{{\left( { – 3 – i} \right)}} = \frac{{ – 3 + 3i – i + {i^2}}}{{9 – {i^2}}} = \frac{{ – 4 + 2i}}{{10}} = – \frac{2}{5} + \frac{1}{5}i\]
Ítem e
\[\frac{{{z_1}}}{{{z_4}}} = \frac{{2 + 3i}}{{1 – i}}.\frac{{1 + i}}{{1 + i}} = – \frac{1}{2} + \frac{5}{2}i\]
Soluciones complejas de ecuaciones cuadráticas
¡Hemos encontrado un número cuyo cuadrado es \(\left( { – 1} \right)\)!
¿Cuánto da \({\left( { – i} \right)^2}\) ?
A partir de ahora, podremos resolver ecuaciones como ésta:
\[{x^2} + 1 = 0\]
Esta ecuación tan sencilla, no tiene solución en \(\mathbb{R}\), pero sí tiene solución en \(\mathbb{C}\):
\[{S_\mathbb{C}} = \left\{ {\;i\;,\; – i\;} \right\}\]
Generalizando, la ecuación cuadrática
\[{x^2} + a = 0\;\;\;,\;con\;\;a > 0\]
no tiene solución en \(\mathbb{R}\) pero tiene dos soluciones en \(\mathbb{C}\): \({x_{1,2}} = \pm \;i\sqrt a \)
Ejemplo
Resolver las ecuaciones:
a) \({x^2} + 5\; = \;0\;\;\)
b) \({x^2} – 4x + 5 = 0\)
Resolución
Ítem a
\[{x^2} + 5 = 0\;\;\;\; \Rightarrow \;\;\;{x^2} = – 5\;\;\;\; \Rightarrow \;\;\;\;x = \sqrt 5 \;i\;\;\;\; \vee \;\;\;x = – \sqrt 5 \;i\]
Ítem b
Podemos usar la fórmula resolvente:
\[\frac{{ – \left( { – 4} \right) \pm \sqrt {{4^2} – 4.1.5} }}{2} = \frac{{4 \pm 2i}}{2} = 2 \pm i\]
\[\; \Rightarrow \;\;\;x = 2 + i\;\; \vee \;\;x = 2 – i\]
Potencias de \(i\)
Las potencias de la unidad imaginaria tienen un comportamiento cíclico, como veremos a continuación:
\[{i^0} = 1\]
\[{i^1} = i\]
\[{i^2} = – 1\]
\[{i^3} = {i^2}.i = – i\]
\[{i^4} = {i^3}.i = 1\]
\[{i^5} = {i^4}.i = i\]
Y así sucesivamente.
¿Cómo podemos determinar cualquier potencia de \(i\) , por ejemplo \({i^{514}}\) ? Dividiendo el exponente por 4, se obtiene: \(514 = 128.4 + 2\)
Entonces resulta:
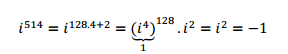
O sea que: \({i^{514}} = {i^2}\) , siendo \(2\) el resto de dividir 514 por 4.
En resumen:
\({i^n} = {i^r}\) , siendo \(r\) el resto de la división de \(n\) por 4 (\(n \in \mathbb{N}\))
Videos relacionados con números complejos

