Sean \({\pi _1}\) y \({\pi _2}\) dos planos no paralelos:
\[{\pi _1}:\;\;{a_1}\;x + {b_1}\;y + {c_1}\;z + {d_1} = 0\]
\[{\pi _2}:\;\;{a_2}\;x + {b_{2\;}}y + {c_2}\;z + {d_2} = 0\]
La intersección de dos planos no paralelos es una recta. Se denomina haz de planos al conjunto de planos que pasan por dicha recta. Uno podría imaginarse al haz de planos como si fueran las hojas de un libro abierto:

Puede demostrarse que la ecuación del haz de planos que pasan por la recta de intersección entre \({\pi _1}\;y\;\;{\pi _2}\;\;\)es la siguiente:
\[{k_1}\left( {{a_1}x + {b_1}y + {c_1}z + {d_1}} \right) + {k_2}\left( {{a_2}x + {b_2}y + {c_2}z + {d_2}} \right) = 0\;\;\;\;\;,\;\;\;{k_1},{k_2} \in \mathbb{R}\]
\[Haz\;de\;planos\;que\;pasan\;por\;la\;recta\;\;\;r = {\pi _1} \cap {\pi _2}\]
Para cada par de valores de \({k_1}\) y \({k_2}\) se obtiene un plano que pasa por la recta \(r\).
Si \({k_1}\; = 0\) y \({k_2} \ne 0\), se obtiene la ecuación del plano \({\pi _2}.\)
Si \({k_2} = 0\) y \({k_1} \ne 0\), se obtiene la ecuación del plano \({\pi _1}\).
Si suponemos que alguna de las constantes es diferente de cero, por ejemplo \({k_1} \ne 0\) , podemos dividir la ecuación del haz por\({k_1}\):
\[\frac{{{k_1}}}{{{k_1}}}\left( {{a_1}x + {b_1}y + {c_1}z + {d_1}} \right) + \frac{{{k_2}}}{{{k_1}}}\left( {{a_2}x + {b_2}y + {c_2}z + {d_2}} \right) = 0\]
Y renombrando \(\frac{{{k_2}}}{{{k_1}}} = k\) queda:
\[\left( {{a_1}x + {b_1}y + {c_1}z + {d_1}} \right) + k\left( {{a_2}x + {b_2}y + {c_2}z + {d_2}} \right) = 0\]
Esta expresión se llama haz reducido. ¿De dónde proviene el nombre de «reducido»?
Falta \({\pi _2}\;\) porque \({\pi _2}\) se corresponde con \({k_1} = 0\). Por lo tanto, en el haz reducido están todos los planos que pasan por \(r = {\pi _1} \cap {\pi _2}\) excepto \({\pi _2}.\)
Ejemplo
Dados los planos:
\[{\pi _1}:\;x + 2y + 3z + 1 = 0\]
\[{\pi _2}:\;\;3x – 5y + z + 10 = 0\]
Encontrar la ecuación de un plano que pase por la recta de intersección entre \({\pi _1}\) y \({\pi _2}\) y que:
a) Sea paralelo al eje \(x\)
b) Sea perpendicular al plano \(x + y + z = 0\)
Se pide encontrar «un plano que pase por la recta de intersección entre \({\pi _1}\) y \({\pi _2}\)«, entonces podemos armar el haz de planos que pasa por dicha recta:
\[\alpha \left( {x + 2y + 3z + 1} \right) + \beta \left( {3x – 5y + z + 10} \right) = 0\]
Parte A
Para que el plano sea paralelo al eje \(x\) su vector normal debe ser \(\vec n = \left( {0,\;b,\;c} \right)\). O sea, el plano debe ser de la forma \(by + cz + d = 0\).
Reescribimos el haz como sigue:
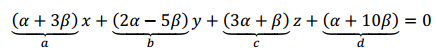
Para que sea paralelo al eje \(x\), \(\alpha + 3\beta = 0\;\; \Rightarrow \alpha = – 3\beta \)
Reemplazando:
\[ – 11\beta y – 8\beta z + 7\beta = 0\]
\[\beta \;\left( { – 11y – 8z + 7} \right) = 0\]
\[{\pi _3}\;\;:\;\;\; – 11y – 8z + 7 = 0\]
Parte B
Ahora queremos un plano del haz que sea perpendicular al plano \(x + y + z = 0\). Dos planos son perpendiculares si sus vectores normales son perpendiculares.
Luego:
\[\left( {1,1,1} \right)\left( {\alpha + 3\beta ,2\alpha – 5\beta ,3\alpha + \beta } \right) = 0\;\]
\[6\alpha – \beta = 0\]
\[\beta = 6\alpha \]
Reemplazando:
\[19\alpha x – 28\alpha y + 9\alpha z + 61\alpha = 0\]
\[\alpha \left( {19x – 28y + 9z + 61} \right) = 0\]
\[19x – 28y + 9z + 61 = 0\]

