Puntos en \({\mathbb{R}^3}\)
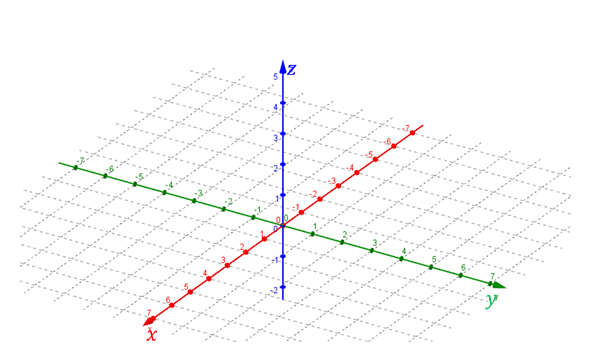
Para ubicar un punto en \({\mathbb{R}^3}\) usaremos como sistema de referencia una terna de ejes perpendiculares entre sí:
- eje \(\color{red}{x}\) (eje de abscisas, en rojo)
- eje \(\color{green}{y}\) (eje de ordenadas, en verde)
- eje \(\color{blue}{z}\) (eje de cotas, en azul)
los cuales se cortan en el punto O (origen de coordenadas).
En el siguiente esquema se ven los tres planos que quedan determinados:
- el plano \(\color{blue}{xy}\) (en azul)
- el plano \(\color{green}{xz}\) ( en verde)
- el plano \(\color{red}{yz}\) (en rojo)
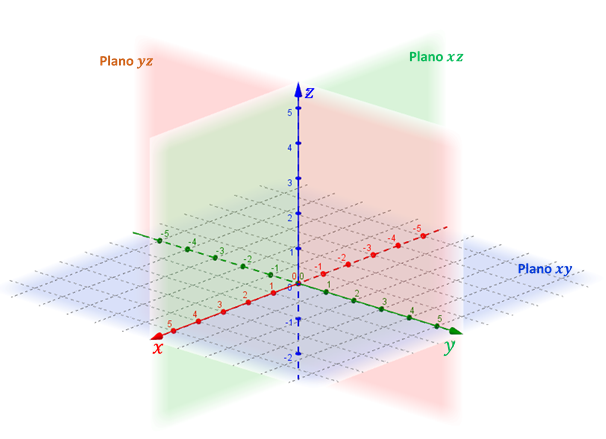
Estos planos se conocen como planos coordenados. El nombre del plano \(xy\) viene de que este plano contiene al eje \(x\) y al eje \(y\). En forma análoga se derivan los nombres de los otros dos planos.
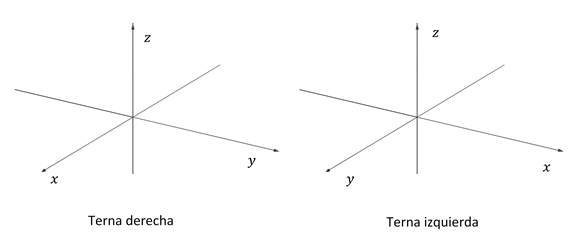
Se puede demostrar que hay dos formas diferentes de armar un sistema de referencia con tres ejes perpendiculares. Una de esas formas se conoce con el nombre de terna derecha (que es la que usaremos en esta materia y la que hemos presentado recién) y la otra como terna izquierda:
Vectores en \({\mathbb{R}^3}\)
Queda establecido un sistema de coordenadas donde todo punto de \({\mathbb{R}^3}\) se define mediante una terna ordenada de números reales: \(P\left( {x,y,z} \right)\), y tiene asociado un vector posición \(\vec p\; = \;\overrightarrow {OP} \; = \;\left( {x,\;y,\;z} \right)\).
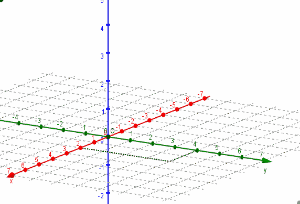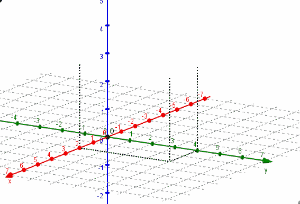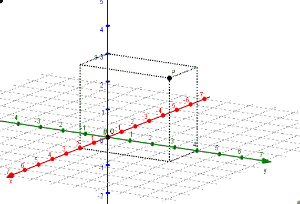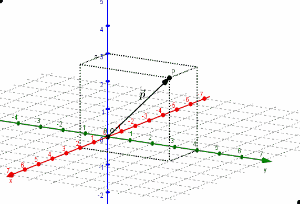
Para dar un ejemplo en el siguiente esquema graficamos al punto \(P\left( {2,4,3} \right)\), y su vector posición \(\vec p = \overrightarrow {OP} \):
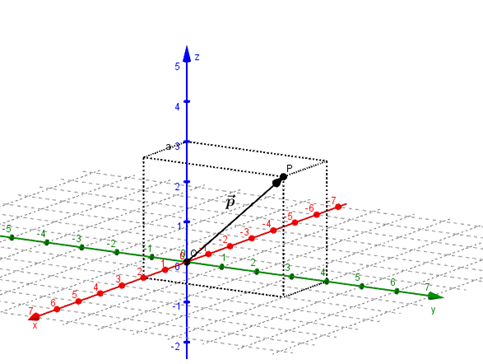
Hemos tomado la misma escala sobre cada uno de los ejes. Pero, como en \({\mathbb{R}^2}\), es posible tomar una escala diferente para cada eje.
En el siguiente GIF les mostramos cómo podría hacerse la gráfica del punto paso a paso:
Operaciones y nociones básicas sobre vectores en \({\mathbb{R}^3}\)
Sean \(\vec v = \left( {{v_x},{v_y},{v_z}} \right)\) y \(\vec w = \left( {{w_x},{w_y},{w_z}} \right)\) vectores de \({\mathbb{R}^3}\).
A continuación definimos algunas operaciones y nociones básicas:
- Igualdad: \(\vec v\; = \;\vec w\;\;\; \Leftrightarrow \;\;\;{v_x} = {w_x}\;,\;\;\;{v_y} = {w_y}\;,\;\;\;{v_z} = \;{w_z}\)
- Suma: \(\vec v + \vec w = \left( {{v_x} + {w_x}\;,\;\;{v_y} + {w_y}\;\;,\;\;{v_z} + {w_z}} \right)\)
- Vector nulo: \(\vec 0\; = \;\left( {0,0,0} \right)\)
- Opuesto de \(\vec v\): \( – \vec v = \left( { – {v_x}, – {v_y}, – {v_z}} \right)\)
- Resta: \(\vec v – \vec w = \vec v + \left( { – \vec w} \right) = \left( {{v_x} – {w_x},{v_y} – {w_y},{v_z} – {w_z}} \right)\)
El producto de un escalar por un vector se define:
\[\vec v = \left( {{v_x},{v_y},{v_z}} \right)\;\;,\;\;k \in \mathbb{R}\;\;\;,k.\vec v = \left( {k.{v_x},k.{v_y},k.{v_z}} \right)\;\]
\(k.\vec v\) es un vector tal que:
- Tiene igual dirección que el vector \(\vec v\)
- Sentido: Si \(k > 0\) entonces \(\vec v\) y \(k.\vec v\) tienen el mismo sentido, si \(k < 0\;\;\;\)entonces \(\;\;\;\;\;\vec v\;\;\) y \(k.\vec v\) tienen sentido opuesto. Si \(\;k = 0\), entonces \(0.\vec v = \vec 0\).
- \(k.\vec v = \left| k \right|\vec v\) . El módulo del vector \(k.\vec v\) es \(\left| k \right|\) veces el módulo del vector \(\vec v\).
¿Cómo es la longitud del vector \(k.\vec v\) respecto de la de \(\vec v\;\)?
Si \(\left| k \right| > 1\) entonces \(\lVert k.\vec v\rVert > \lVert \vec v\rVert\)
Si \(\left| k \right| < 1\) entonces \(\lVert k.\vec v\rVert < \lVert \vec v\rVert\)
Si \(\left| k \right| = 1\) entonces \(\lVert k.\vec v\rVert = \lVert \vec v\rVert\)
Notación
\(\lVert \vec v\rVert\): módulo o norma de un vector
\(\left| k \right|:\;\)módulo o valor absoluto de un número real
La definición de producto de un escalar por un vector permite enunciar una condición para que dos vectores (no nulos) sean paralelos:
\[\vec v\parallel \vec w\;\; \Leftrightarrow \;\;\;\vec v\; = \;k.\vec w\;\;\;con\;k \in \mathbb{R}\]
Ejemplo 1
Dados \(\vec u = \left( {1, – 1,1} \right)\;,\;\vec v = \left( {2,0,2} \right)\;\;y\;\overrightarrow {\;w} = \left( { – 1,3, – 1} \right)\) , ¿Existen \(\alpha ,\beta \in \mathbb{R}\) tales que
\(\vec w = \alpha .\vec u + \beta .\vec v\;\)?
Para responderlo escribiremos la igualdad y trataremos de calcular \(\alpha \), y \(\beta \):
\[\left( { – 1,3, – 1} \right) = \alpha .\left( {1, – 1,1} \right) + \beta .\left( {2,0,2} \right)\;\]
\[\left( { – 1,3, – 1} \right) = \left( {\alpha + 2\beta , – \alpha ,\alpha + 2\beta } \right)\]
\[\left\{ {\begin{array}{*{20}{c}}{ – 1 = \alpha + 2\beta }\\{3 = – \alpha }\\{ – 1 = \alpha + 2\beta }\end{array}} \right.\; \Rightarrow \;\;\alpha = – 3 \wedge \beta = 1\]
\[\left( { – 1,3, – 1} \right) = – 3.\left( {1, – 1,1} \right) + 1.\left( {2,0,2} \right)\;\]
Como existen \(\alpha ,\beta \in \mathbb{R}\) tales que \(\vec w = \alpha .\vec u + \beta .\vec v\) , diremos que \(\vec w\) es combinación lineal de \(\vec u\) y \(\vec v\). Más adelante desarrollaremos el concepto de combinación lineal.
Podemos visualizar esto en un gráfico:
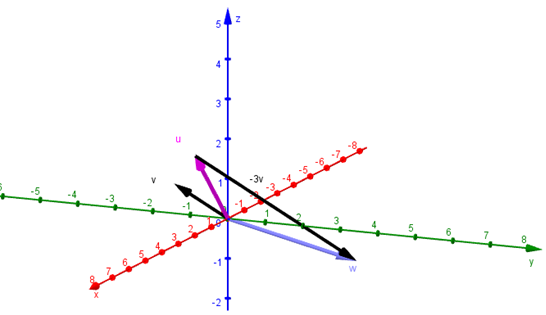
Pero esto puede llevarnos a la pregunta:
Dados tres vectores \(\vec u,\;\overrightarrow {\;v} ,\;\overrightarrow {\;w} \) de \({\mathbb{R}^3}\), ¿es siempre posible encontrar los números reales \(\alpha \;y\;\beta \) tales que \(\vec w = \alpha .\vec u + \beta .\vec v\) ?
Veamos otro ejemplo para responderla.
Ejemplo
Si los vectores fueran:
\[\vec u = \left( {2, – 3,4} \right)\]
\[\vec v = \left( { – 5,1,0} \right)\]
\[\vec w = \left( {4,2,1} \right)\]
Veamos si existen \(\alpha ,\beta \in \mathbb{R}\) tal que \(\vec w = \alpha .\vec u + \beta .\vec v\;\):
\[\left( {4,2,1} \right) = \alpha \left( {2, – 3,4} \right) + \beta .\left( { – 5,1,0} \right)\]
\[\left( {4,2,1} \right) = \left( {2\alpha , – 3\alpha ,4\alpha } \right) + \left( { – 5\beta ,1\beta ,0} \right)\]
\[\left( {4,2,1} \right) = \left( {2\alpha – 5\beta , – 3\alpha + 1\beta ,4\alpha } \right)\]
\[\left\{ {\begin{array}{*{20}{c}}{2\alpha – 5\beta = 4}\\{ – 3\alpha + \beta = 2}\\{4\alpha = 1}\end{array}} \right.\]
Es un sistema con tres ecuaciones y dos incógnitas. Podemos despejar \(\alpha \;y\;\beta \) a partir de dos de las ecuaciones (por ejemplo las dos últimas):
\[\alpha = \frac{1}{4}\]
\[\beta = \frac{{11}}{4}\]
Pero luego debemos verificar si estos valores satisfacen primera ecuación.
Reemplazamos en: \(2\alpha – 5\beta = 4\):
\[\frac{2}{4} – \frac{{55}}{4} \ne 4\]
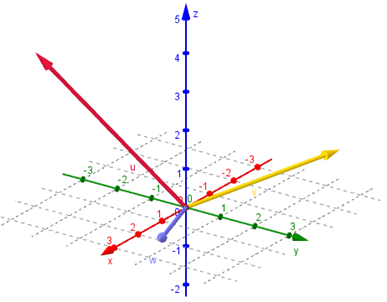
No se verifica la ecuación, por lo tanto no existen los escalares \(\alpha \;y\;\beta \) que satisfagan la igualdad. En otras palabras, diremos que \(\vec w\) no es una combinación lineal de \(\vec u\) y de \(\vec v\).
Como puede observarse en la imagen, los tres vectores no están contenidos en un mismo plano (no son coplanares), entonces ninguno de ellos puede obtenerse como combinación lineal de los otros dos:
Propiedades de la suma de vectores y del producto por un escalar
Sean \(\vec u,\vec v,\vec w \in {\mathbb{R}^3}\;\;y\;\;\alpha ,\;\beta \in \mathbb{R}\).
Vimos que: \(\vec u + \vec v \in {\mathbb{R}^3}\) y \(\alpha \vec u \in {\mathbb{R}^3}\). Estas operaciones verifican las siguientes propiedades:
- \(\vec u + \vec v = \vec v + \vec u\;\;\;\;\)
- \(\left( {\vec u + \vec v} \right) + \vec w = \vec u + \left( {\vec v + \vec w} \right)\;\;\;\;\)
- \(\vec u + \vec 0 = \vec 0 + \vec u = \vec u\;\;\;\;\;\)
- \(\vec u + \left( { – \vec u} \right) = \left( { – \vec u} \right) + \vec u = \vec 0\)
- \(\alpha \left( {\vec u + \vec v} \right) = \alpha \vec u + \alpha \vec v\)
- \(\left( {\alpha + \beta } \right)\vec u = \alpha \vec u + \beta \vec u\)
- \(\alpha \left( {\beta \vec u} \right) = \left( {\alpha \beta } \right)\vec u\)
- \(1\vec u = \vec u\)
Módulo o norma de un vector en \({\mathbb{R}^3}\)
Nos interesa hallar una fórmula para calcular el módulo o norma de un vector. En \({\mathbb{R}^3}\) el módulo es la longitud del vector. Para deducirla usaremos los triángulos rectángulos que quedan determinados tal como se muestra en la siguiente figura:
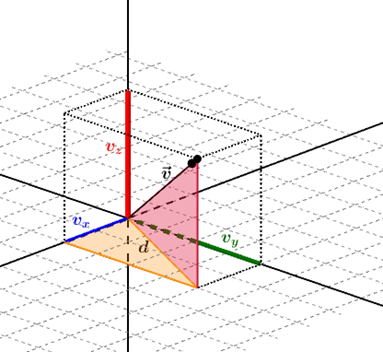
Aplicando el teorema de Pitágoras sobre el triángulo sombreado de naranja:
\[{d^2} = v_x^2 + v_y^2\;\;\;\;\;\;\;\;\left( 1 \right)\]
Aplicando el teorema de Pitágoras sobre el triangulo sombreado de rosa:
\[{\lVert \vec v\rVert^2} = {d^2} + v_z^2\;\;\;\;\;\;\;\;\;\left( 2 \right)\;\]
Sustituyendo \(\left( 1 \right)\) en \(\left( 2 \right)\):
\[{\lVert \vec v\rVert^2} = v_x^2 + v_y^2 + v_z^2\]
Aplicando raíz cuadrada a ambos miembros:
Propiedades del módulo o norma de un vector
- \(\ \lVert \vec v\rVert \ge 0\;\;\; \wedge \;\;\;\lVert \vec v\rVert = 0 \Leftrightarrow \;\vec v = \vec 0\)
- \(\;\lVert k.\vec v \rVert = \left| k \right|\;\lVert \vec v\rVert,\;\;k \in \mathbb{R}\;\)
- Desigualdad triangular: \(\lVert \vec v + \vec w\rVert \le \lVert \vec v \rVert + \lVert \vec w \rVert\)
El nombre de desigualdad triangular se conecta con la propiedad que dice: «La longitud de cada lado de un triángulo es menor que la suma de las longitudes de los otros dos».
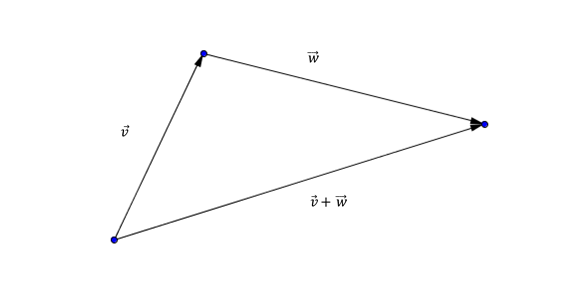
¿Qué condiciones tienen que cumplir los vectores \(\vec v\) y \(\vec w\) para que se verifique la igualdad: \(\lVert \vec v + \vec w \rVert = \lVert \vec v \rVert + \lVert \vec w\rVert \;\)?
Ejemplo
Sean \(v = \left( { – 1,1,2} \right)\) y \(w = \left( {3,0, – 4} \right)\;\) calcular:
a) \(\lVert \vec v\rVert\)
b) \(\lVert – 2\vec v\rVert\)
c) \(\lVert \vec w\rVert\)
d) \(\lVert \vec v + \vec w\rVert\)
Resolución
\[\lVert \vec v\rVert = \sqrt {{{\left( { – 1} \right)}^2} + {1^2} + {2^2}} = \sqrt 6 \]
\[ \lVert – 2\vec v\rVert\ = \sqrt {{{\left( { – 2} \right)}^2} + {2^2} + {4^2}} = \sqrt {24} = 2\sqrt 6 \]
\[\lVert \vec w\rVert\ = \sqrt {{3^2} + {0^2} + {{\left( { – 4} \right)}^2}} = 5\]
\[\lVert \vec v + \vec w\rVert = \lVert \left( {2,1, – 2} \right)\rVert = \sqrt {{2^2} + {1^2} + {{\left( { – 2} \right)}^2}} = 3\]
Observemos que \( \lVert \vec v + \vec w\rVert \ne \lVert \vec v\rVert + \lVert \vec w\rVert\)
Vector determinado por dos puntos
Dados los puntos \(A\left( {{X_A},{Y_A},{Z_A}} \right)\) y \(B\left( {{X_B},{Y_B},{Z_B}} \right)\), el vector \(\overrightarrow {AB} \), con origen en \(A\) y extremo en \(B\), puede obtenerse cómo sigue:
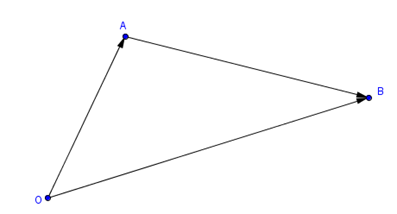
\[\overrightarrow {OA} + \overrightarrow {AB} = \overrightarrow {OB} \]
\[ \Rightarrow \overrightarrow {AB} = \overrightarrow {OB} – \overrightarrow {OA} = \left( {{X_B},{Y_B},{Z_{,B}}} \right) – \left( {{X_A},{Y_A},{Z_A}} \right)\]
\[ \Rightarrow \overrightarrow {AB} = \left( {{X_B} – {X_A},{Y_B} – {Y_A},{Z_B} – {Z_A}} \right)\]
Ejemplo
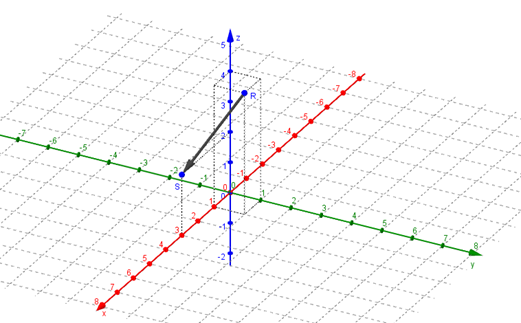
Sean \(R\left( {1,1,4} \right)\) y \(S\left( {3,0,2} \right)\) dos puntos de \({\mathbb{R}^3}\), hallar las componentes del vector \(\overrightarrow {RS} \).
Según hemos visto:
\[\overrightarrow {RS} = \left( {3 – 1,\;0 – 1,\;2 – 4} \right) = \left( {2, – 1, – 2} \right)\]
Veamos esto en un gráfico:
Distancia entre dos puntos
Problema
¿Cómo podríamos calcular la distancia entre \(R\left( {1,1,4} \right)\) y \(S\left( {3,0,2} \right)\)?
Para hallar esta distancia armamos el vector \(\overrightarrow {RS} \) (o \(\overrightarrow {SR} \) ) y calculamos su módulo:
\[\overrightarrow {RS} = \left( {2, – 1, – 2} \right)\]
\[\lVert \overrightarrow {RS}\rVert = \sqrt {{2^2} + {{\left( { – 1} \right)}^2} + {{\left( { – 2} \right)}^2}} = \sqrt {4 + 1 + 4} = \sqrt 9 = 3\]
\[ \Rightarrow d\left( {R,S} \right) = 3\]
En general
Dados dos puntos \(A\left( {{x_A},{y_A},{z_A}} \right)\) y \(B\left( {{x_B},{y_B},{z_B}} \right)\) la distancia entre los mismos se calcula:
Problema
Encontrar, si es posible, todos los puntos del eje \(z\) cuya distancia al punto \(A\left( {3,2,1} \right)\) es \(5\).
Es recomendable hacer una figura de análisis del problema:
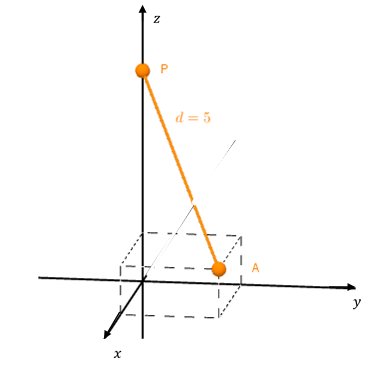
Un punto del eje \(z\) tiene la forma \(P\left( {0,0,z} \right)\). Construyamos el vector desde un punto genérico cualquiera del eje \(z\) hasta \(A\).
\[\overrightarrow {PA} = \left( {3,\;2,\;1 – z} \right)\]
Se pide que el módulo (o norma) de \(\overrightarrow {PA} \) sea 5, entonces:
\[\overrightarrow {PA} = \sqrt {{3^2} + {2^2} + {{\left( {1 – z} \right)}^2}} = \sqrt {13 + 1 – 2z + {z^2}} = \sqrt {14 – 2z + {z^2}} = 5\]
\[25 = 14 – 2z + {z^2}\;\; \Rightarrow {z^2} – 2z – 11 = 0\;\]
\[z = \frac{{2 + \sqrt {4 – 4.1.\left( { – 11} \right)} }}{2}\;\;\;\; \vee \;\;\;\;z = \frac{{2 – \sqrt {4 – 4.1.\left( { – 11} \right)} }}{2}\;\;\;\]
\[z = \frac{{2 + \sqrt {48} }}{2}\;\;\;\; \vee \;\;\;\;z = \frac{{2 – \sqrt {48} }}{2}\;\;\;\]
\[z = 1 + \sqrt {12} \cong 4,46\;\;\;\; \vee \;\;\;\;z = 1 – \sqrt {12} \cong – 2,46\;\;\]
Hemos llegado a que \(z\) puede tomar dos valores distintos. Entonces existen dos puntos del eje \(z\) cuya distancia al punto \(A\left( {3,2,1} \right)\) es 5. Son:
\[{P_1}\left( {0,\;0,\;1 + \sqrt {12} } \right)\;\;\; \wedge \;\;\;{P_2}\left( {0,\;0,\;1 – \sqrt {12} } \right)\]
Expresión canónica de un vector
Recordemos que todo vector de \({\mathbb{R}^2}\) puede expresarse como combinación lineal de los versores canónicos \( \check i = \left( {1,0} \right)\) y \( \check j = \left( {0,1} \right)\).
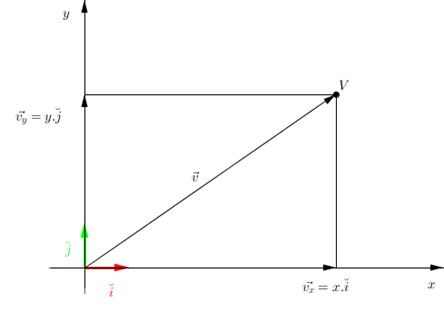
\[\vec v = \left( {x,y} \right)\]
\[\vec v = x\left( {1,0} \right) + y\left( {0,1} \right)\]
\[\vec v = x.\check i + y.\check j \]
En forma análoga, todo vector de \({\mathbb{R}^3}\) puede expresarse como combinación lineal de los versores canónicos:
\[\check i = \left( {1,0,0} \right)\]
\[\check j = \left( {0,1,0} \right)\]
\[\check k = \left( {0,0,1} \right)\]
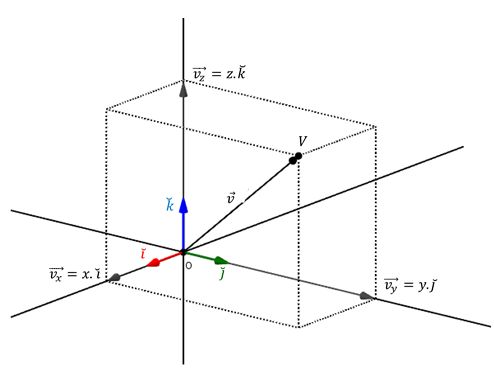
\[\vec v = \left( {x,y,z} \right) = x\left( {1,0,0} \right) + y\left( {0,1,0} \right) + z\left( {0,0,1} \right)\]
\(\vec v = x.\check i + y.\check j + z.\check k \) (expresión canónica)
Ángulos directores y cosenos directores de un vector
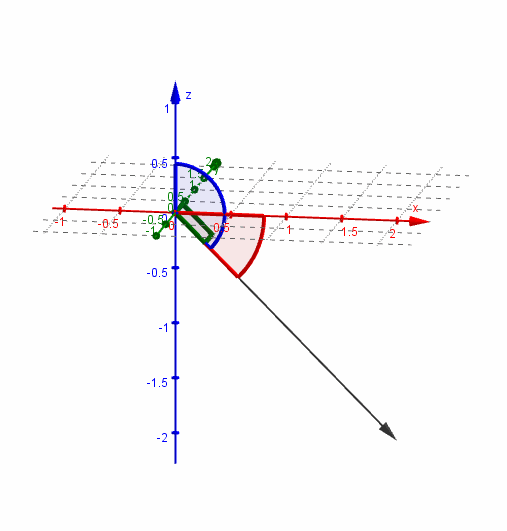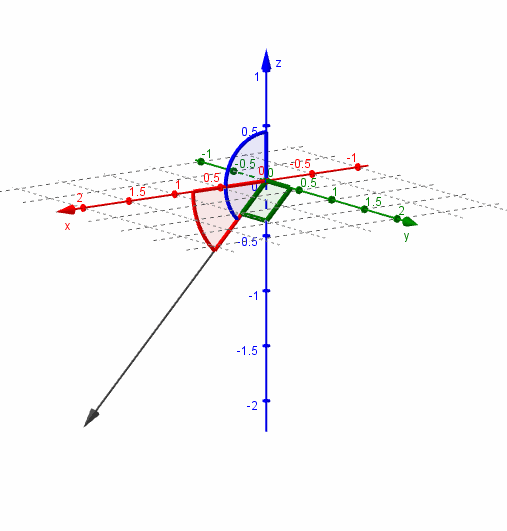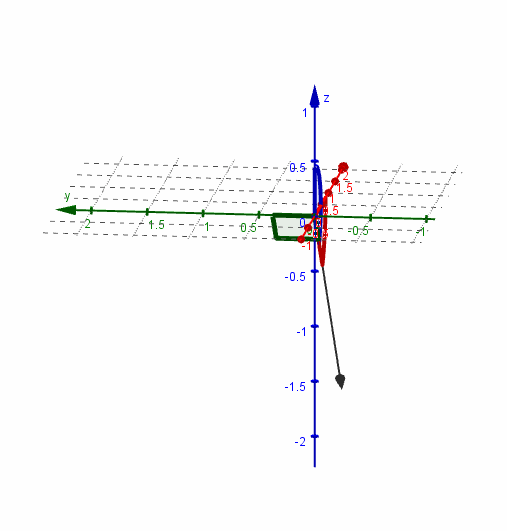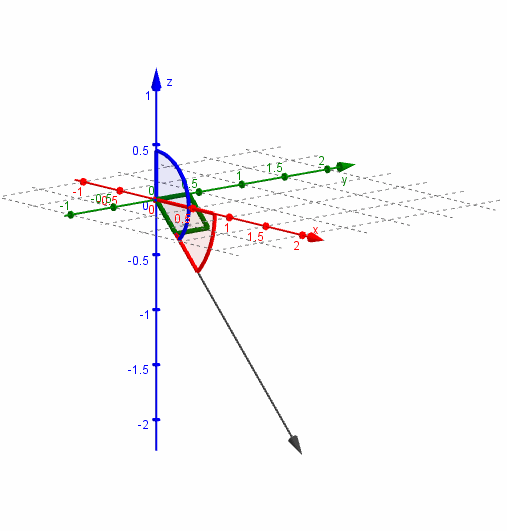
Se denominan ángulos directores de un vector a los ángulos determinados por el vector y cada uno de los semiejes positivos, como se muestra en la siguiente figura:
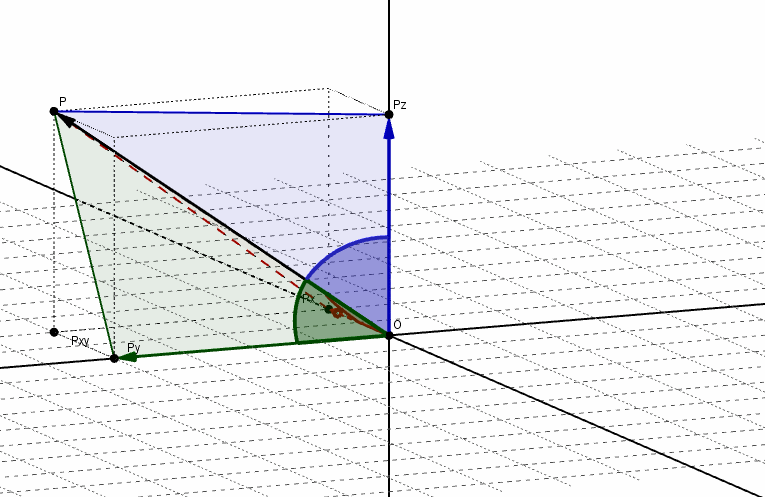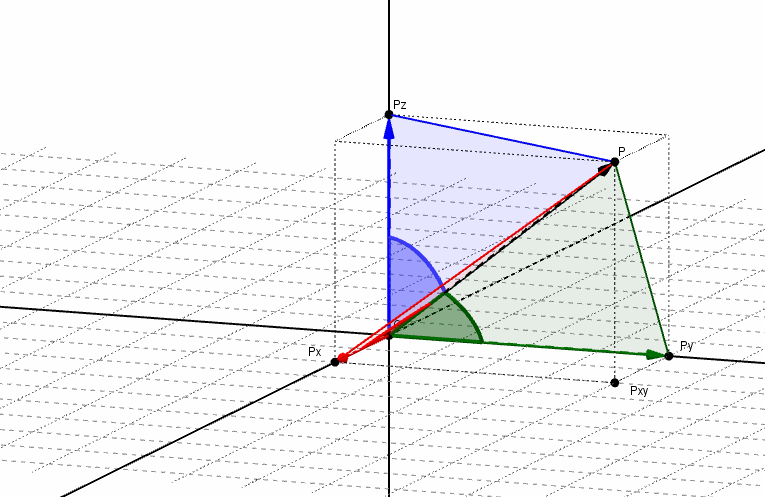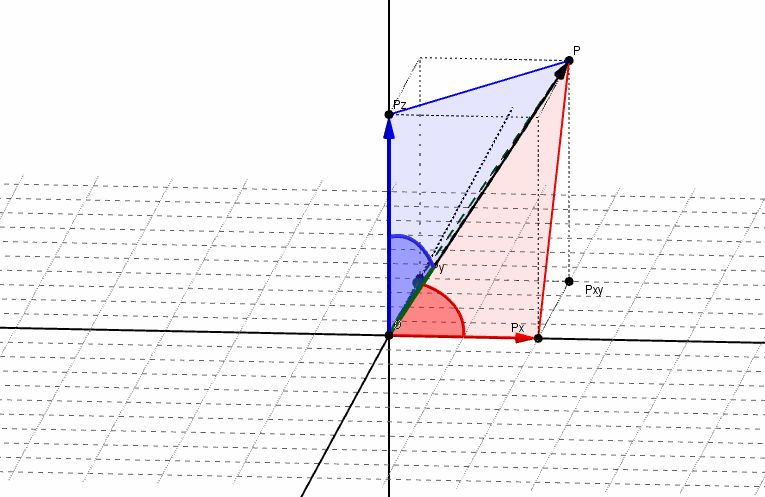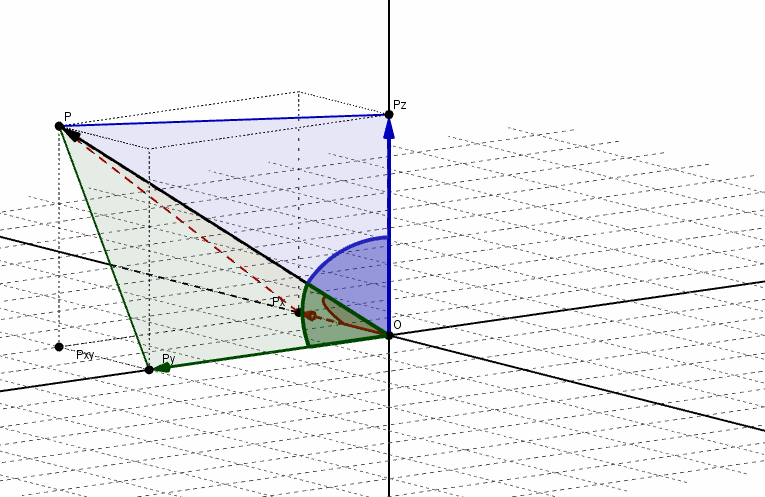
Los cosenos de dichos ángulos se llaman cosenos directores del vector. Aplicando relaciones trigonométricas, podemos obtener los cosenos directores:
\[\cos \left( \alpha \right) = \frac{{{v_x}}}{{\lVert \vec v\rVert}}\;\;,\;\;\;cos\left( \beta \right) = \frac{{{v_y}}}{{\lVert \vec v\rVert}}\;\;,\;\;\cos \left( \gamma \right) = \frac{{{v_z}}}{{\lVert \vec v\rVert}}\]
Por lo tanto, los ángulos directores son:
\[\alpha = arcos\left( {\frac{{{v_x}}}{{\lVert \vec v\rVert}}} \right)\;\;,\;\;\;\beta = arcos\left( {\frac{{{v_y}}}{{\lVert \vec v\rVert}}} \right)\;\;,\;\;\gamma = arcos\left( {\frac{{{v_z}}}{{\lVert \vec v\rVert}}} \right)\]
Donde \(\alpha ,\beta ,\gamma \) están comprendidos entre \(0\) y \(\pi \).
Propiedad
\[{\cos ^2}\left( \alpha \right) + {\cos ^2}\left( \beta \right) + {\cos ^2}\left( \gamma \right) = 1\]
Demostración
Sustituyamos los cosenos por los cocientes correspondientes:
\[{\cos ^2}\left( \alpha \right) + {\cos ^2}\left( \beta \right) + {\cos ^2}\left( \gamma \right) = {\left( {\frac{{{v_x}}}{{\lVert \vec v\rVert}}} \right)^2} + {\left( {\frac{{{v_y}}}{{\lVert \vec v\rVert}}} \right)^2} + {\left( {\frac{{{v_z}}}{{\lVert \vec v\rVert}}} \right)^2} = \frac{{v_x^2 + v_y^2 + v_z^2}}{{{{\vec v}^2}}} = \frac{{{{\lVert \vec v\rVert}^2}}}{{{{\lVert \vec v\rVert}^2}}} = 1\]
Ejemplo
Hallar los ángulos directores de \( \vec v = \left( {2,0, – 2} \right)\)
Resolución
Hallemos el módulo del vector:
\[\lVert \vec v\rVert = \sqrt {{2^2} + {0^2} + {{\left( { – 2} \right)}^2}} = \sqrt 8 = 2\sqrt 2 \]
Ahora calculamos los ángulos con el arco coseno de los cocientes:
\[\alpha = \arccos \left( {\frac{2}{{2\sqrt 2 }}} \right) = 45^\circ \]
\[\beta = \arccos \left( {\frac{0}{{2\sqrt 2 }}} \right) = 90^\circ \]
\[\gamma = \arccos \left( {\frac{{ – 2}}{{2\sqrt 2 }}} \right) = 135^\circ \]
Veamos una gráfica del vector y sus ángulos directores:
Versor asociado a un vector
Dado un vector no nulo \(\vec v\), se denomina versor asociado al vector unitario (de módulo 1) que tiene igual dirección y sentido que \(\vec v\).
Dado \(\vec v\) distinto de \(\vec 0\), su versor asociado se obtiene así:
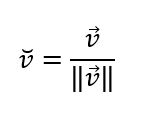
Tomando en cuenta los cosenos directores,
\[\vec v = \left( {\lVert \vec v\rVert\cos \alpha \;,\;\;\;\lVert \vec v\rVert\cos \beta \;,\;\;\;\lVert \vec v\rVert\cos \gamma } \right)\]
Entonces
\[\frac{{\vec v}}{{\lVert \vec v\rVert}} = \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over v} = \left( {\cos \alpha \;,\;\cos \beta \;,\cos \gamma \;} \right)\]
O sea, las componentes del versor \(\check v \) son los cosenos directores de \(\vec v\).

