Sea \(A \in {\mathbb{R}^{n \times n}}\) diagonalizable. Es decir, existe \(P \in {\mathbb{R}^{n \times n}}\) inversible tal que:
\[{P^{ – 1}}AP = D\]
donde \(D\) es una matriz diagonal.
Recordemos que:
\[A\;es\;diagonalizable\; \Leftrightarrow \;A\;tiene\;n\;autovectores\;LI\;en\;{\mathbb{R}^n}\]
En la diagonal \(D\) que se obtiene están los autovalores ordenados de acuerdo con el orden de los autovectores en las columnas de \(P\):
\[{P^{ – 1}}AP = D = \left( {\begin{array}{*{20}{c}}{{\lambda _1}}&0&0\\0& \ddots &0\\0&0&{{\lambda _n}}\end{array}} \right)\]
Cómo veremos a continuación esta relación permite calcular fácilmente potencias de matrices diagonalizables.
Considerando que \({P^{ – 1}}.A.P = D\) y multiplicando a la izquierda por \(P\) y a la derecha por \({P^{ – 1}}\), se obtiene:
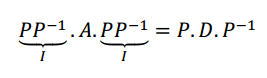
\[ \Rightarrow \;\;\;A = PD{P^{ – 1}}\]
Ahora, calculemos \({A^2}\):
\[{A^2} = \left( {PD{P^{ – 1}}} \right).\left( {PD{P^{ – 1}}} \right) = PD{P^{ – 1}}.PD{P^{ – 1}}\]
El producto de matrices es asociativo, entonces:
\[{A^2} = P\;D\;I\;D\;{P^{ – 1}}\]
\[{A^2} = P{D^2}{P^{ – 1}}\]
En general, en términos prácticos, es mucho más sencillo calcular \({D^2}\) que \({A^2}\), y más aún en caso de que los exponentes sean mayores.
Las potencias de una matriz diagonal se obtienen calculando las potencias de los elementos que están en la diagonal principal:
\[D = \left( {\begin{array}{*{20}{c}}{{\lambda _1}}& \ldots &0\\ \vdots & \ddots & \vdots \\0& \ldots &{{\lambda _n}}\end{array}} \right)\;\; \Rightarrow \;\;{D^k} = \left( {\begin{array}{*{20}{c}}{{\lambda _1}^k}& \ldots &0\\ \vdots & \ddots & \vdots \\0& \ldots &{{\lambda _n}^k}\end{array}} \right)\]
En conclusión hemos encontrado que para cualquier matriz \(A\) diagonalizable:
Ejemplo 1
Calcular \({A^{10}}\) , siendo \(A = \left( {\begin{array}{*{20}{c}}1&3\\2&2\end{array}} \right)\)
Resolución
Vamos a intentar diagonalizar \(A\) para no tener que calcular:
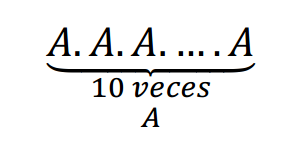
Si \(A\) es diagonalizable será posible hacer:
\[{A^{10}} = P{D^{10}}{P^{ – 1}}\]
Veamos si \(A\) es diagonalizable. Se puede verificar que sus autovalores son:
\[{\lambda _1} = 4\;\;\;,\;\;\;{\lambda _2} = – 1\]
Ya es posible afirmar que es diagonalizable, porque autovectores asociados a autovalores distintos son LI.
El lector puede verificar que los autoespacios son los siguientes:
\[{S_{{\lambda _1} = 4}} = \left\{ {\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right):\;\;y = x} \right\}\]
\[{S_{{\lambda _2} = – 1}} = \left\{ {\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right):\;\;y = – \frac{2}{3}x} \right\}\]
Luego podemos armar la matriz \(P\):
\[P = \left( {\begin{array}{*{20}{c}}1&3\\1&{ – 2}\end{array}} \right)\]
Obtenemos su inversa:
\[{P^{ – 1}} = \left( {\begin{array}{*{20}{c}}{\frac{2}{5}}&{\frac{3}{5}}\\{\frac{1}{5}}&{ – \frac{1}{5}}\end{array}} \right)\]
Calculamos el producto:
\[{P^{ – 1}}AP = \left( {\begin{array}{*{20}{c}}4&0\\0&{ – 1}\end{array}} \right) = D\]
Por la propiedad que hemos visto:
\[{A^{10}} = P{D^{10}}{P^{ – 1}}\]
\[ \Rightarrow \;\;\;\;{A^{10}} = \left( {\begin{array}{*{20}{c}}1&3\\1&{ – 2}\end{array}} \right)\left( {\begin{array}{*{20}{c}}{{4^{10}}}&0\\0&{{{\left( { – 1} \right)}^{10}}}\end{array}} \right).\left( {\begin{array}{*{20}{c}}{\frac{2}{5}}&{\frac{3}{5}}\\{\frac{1}{5}}&{ – \frac{1}{5}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{419431}&{629145}\\{419430}&{629146}\end{array}} \right)\]

