El siguiente es el enunciado y resolución completa del primer parcial de álgebra y geometría analítica tomado el día 22-04-2017, en el curso semi-presencial.

EJERCICIO 1
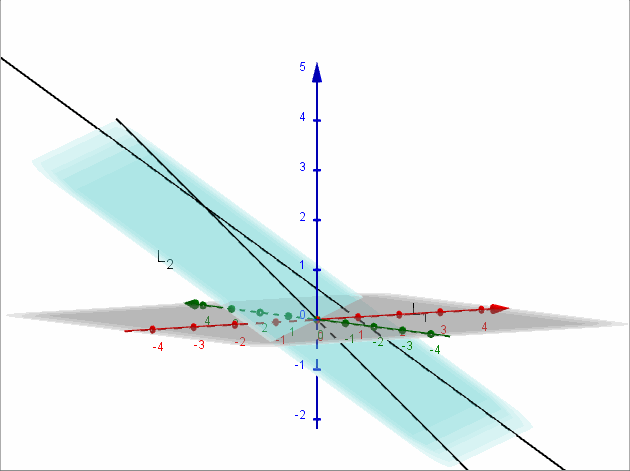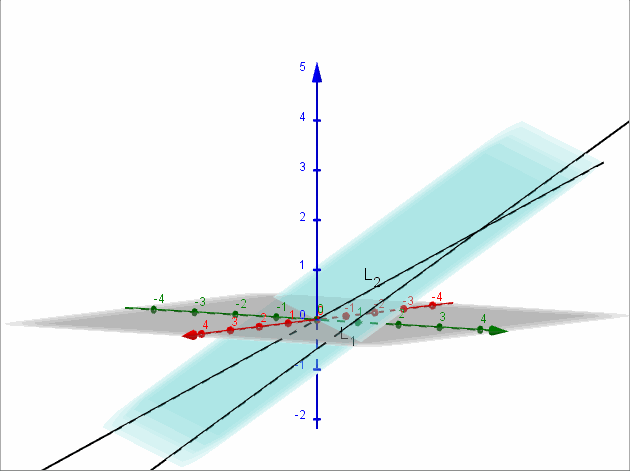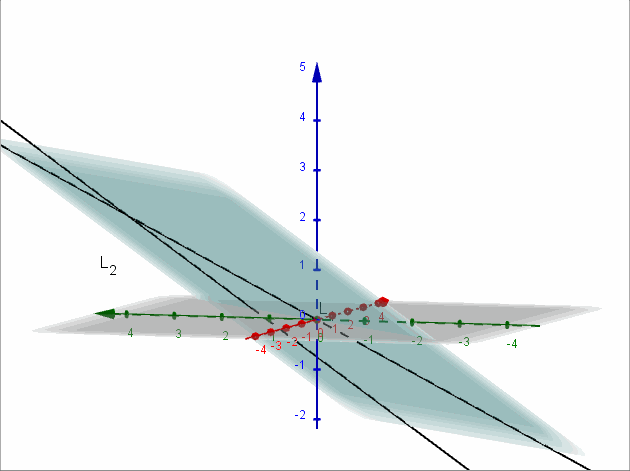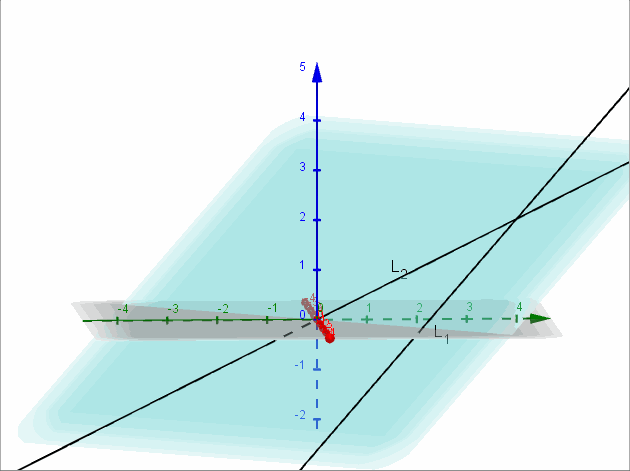
Sean \({L_1}:\left( {x,y,z} \right) = \left( {2,2,a} \right) + \beta \left( {1, – 1, – 1} \right)\) y \({L_2}:\left( {x,y,z} \right) = \left( {a,2,1} \right) + \lambda \left( {0,2,1} \right)\)
Encontrar, si es posible, \(a \in \mathbb{R}\) para que las rectas \({L_1}\) y \({L_2}\) sean coplanares. Para el valor de \(a\) obtenido, hallar el plano contiene a las rectas dadas.
Resolución
Queremos que \({L_1}\) y \({L_2}\) sean coplanares. Podemos plantear la condición de coplanaridad y despejar \(a\):
\({L_1}\) y \({L_2}\) son coplanares \( \Leftrightarrow \overrightarrow {{v_1}} \times \overrightarrow {{v_2}} \left( {\overrightarrow {{P_1}{P_2}} } \right) = 0\)
Construimos un vector \(\overrightarrow {{P_1}{P_2}} \), tomando los puntos de paso de las ecuaciones:
\[\overrightarrow {{P_1}{P_2}} = \left( {a,2,1} \right) – \left( {2,2,a} \right) = \left( {a – 2,0,1 – a} \right)\]
Ahora calculamos el producto vectorial entre los vectores directores de las rectas:
\[\overrightarrow {{v_1}} \times \overrightarrow {{v_2}} = \left| {\begin{array}{*{20}{c}}i&j&k\\1&{ – 1}&{ – 1}\\0&2&1\end{array}} \right| = \left( {1, – 1,2} \right)\]
Calculamos el producto escalar:
\[\overrightarrow {{v_1}} \times \overrightarrow {{v_2}} \left( {\overrightarrow {{P_1}{P_2}} } \right) = \left( {1, – 1,2} \right)\left( {a – 2,0,1 – a} \right) = 0\]
\[ \Rightarrow a – 2 + 2 – 2a = 0\]
\[ \Rightarrow a = 0\]
Para que las rectas sean coplanares debe ser \(a = 0\).
Para hallar la ecuación del plano que las contiene recordemos que un vector normal del plano se puede hallar con el producto vectorial de los vectores directores de las rectas. Ese producto ya lo hicimos y obtuvimos el vector \(\left( {1, – 1,2} \right)\).
Entonces la ecuación del plano debe ser:
\[{\rm{\;}}x – y + 2z + d = 0\]
Para hallar el valor de \(d\) podemos reemplazar en la ecuación del plano por un punto \(\left( {2,2,0} \right) \in \pi \):
\[2.0 + d = 0 \Rightarrow d = 0\]
Finalmente la ecuación del plano que las contiene queda:
\[x – y + 2z = 0\]
EJERCICIO 2
Dado el plano \(\pi :{\rm{\;}}\left( {x,{\rm{\;}}y,{\rm{\;}}z} \right) = \left( {0,{\rm{\;}}1,{\rm{\;}}2} \right) + {t_1}{\rm{\;}}\left( { – 1,{\rm{\;}} – 1,{\rm{\;}}2} \right) + {\rm{\;}}{t_2}{\rm{\;}}\left( {1,{\rm{\;}}1,{\rm{\;}}0} \right)\) con \({t_1},{\rm{\;}}{t_2} \in \mathbb{R}\).
a) Hallar la proyección ortogonal del punto \(A\left( {2,1,3} \right)\) sobre el plano \(\pi \).
b) Obtener todos los puntos del eje \(y\) que distan \(\sqrt 2 \) unidades del plano \(\pi \).
Resolución del ejercicio 2
Ítem a
Hallemos primero la ecuación general del plano. Hacemos el producto de los vectores directores del plano:
\[\overrightarrow {{n_\pi }} = \left| {\begin{array}{*{20}{c}}i&j&k\\{ – 1}&{ – 1}&2\\1&1&0\end{array}} \right| = \left( { – 2,2,0} \right)\]
Entonces una ecuación es:
\[\pi : – 2x + 2y + d = 0\]
Cómo sabemos que el punto \(\left( {0,1,2} \right) \in \pi \), debe satisfacer la ecuación del plano:
\[ \Rightarrow 2 + d = 0\]
\[ \Rightarrow {\rm{d}} = – 2\]
\[ \Rightarrow {\rm{\;}}\pi : – 2x + 2y – 2 = 0\]
Dividiendo ambos miembros por 2 nos queda una ecuación simplificada:
\[\pi : – x + y – 1 = 0\]
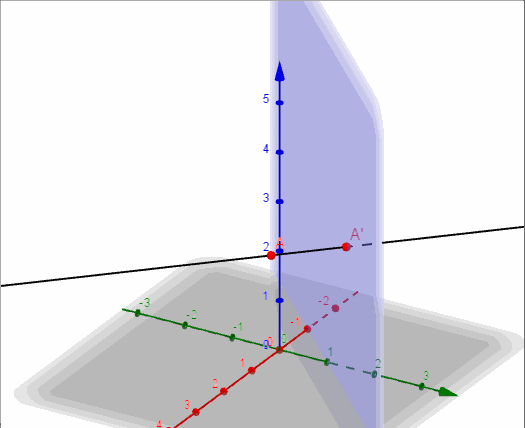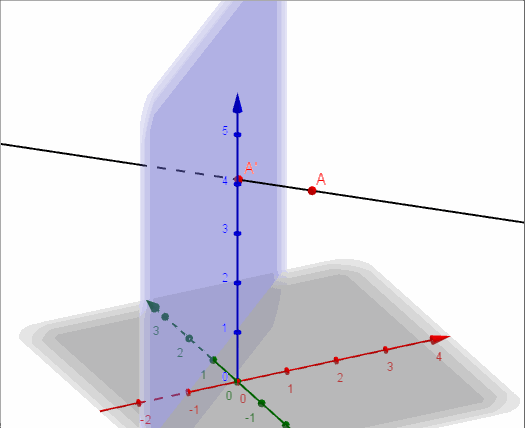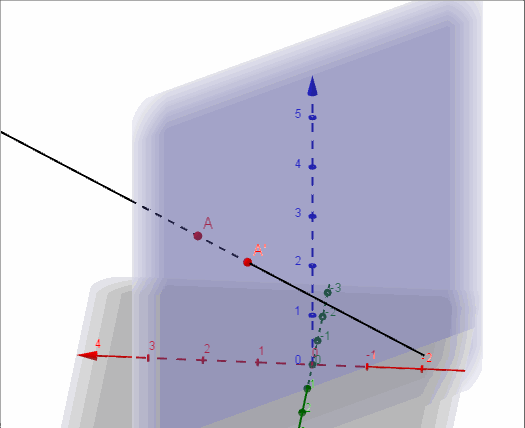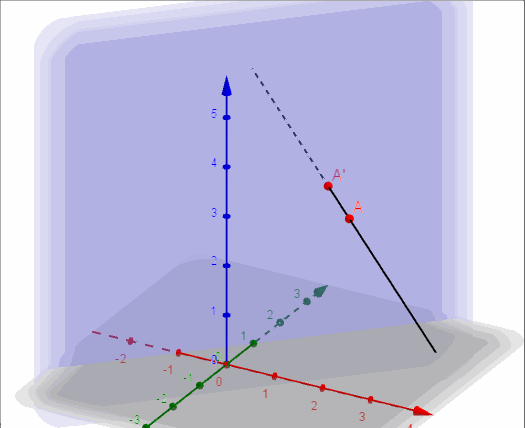
Ahora construimos una recta auxiliar perpendicular a \(\pi \) que pasa por \(A\):
\[r:\left( {x,y,z} \right) = \left( {2,1,3} \right) + \lambda \left( { – 1,1,0} \right)\]
\[r:{\rm{\;}}\left\{ {\begin{array}{*{20}{c}}{x = 2 – \lambda }\\{y = 1 + \lambda }\\{z = 3}\end{array}} \right.\]
Y buscamos la intersección entre la recta \(r\) y el plano \(\pi \):
\[ – \left( {2 – \lambda } \right) + \left( {1 + \lambda } \right) – 1 = 0\]
\[ \Rightarrow 2\lambda – 2 = 0\]
\[ \Rightarrow \lambda = 1\]
\[r \cap \pi = A{\rm{‘}} = \left( {1,2,3} \right)\]
Ítem b
Un punto del eje \(y\) es de la forma \({P_y} = \left( {0,y,0} \right)\). Reemplazamos en la ecuación de distancia de punto a un plano:
\[d\left( {{P_y},\pi } \right) = \frac{{\left| { – 0 + y – 1} \right|}}{{\sqrt {{{\left( { – 1} \right)}^2} + {1^2} + {0^2}} }} = \sqrt 2 \]
\[ \Rightarrow \frac{{\left| {y – 1} \right|}}{{\sqrt 2 }} = \sqrt 2 \]
\[ \Rightarrow \left| {y – 1} \right| = 2\]
\[ \Rightarrow y = 3{\rm{\;\;}} \vee {\rm{\;\;}}y = – 1\]
Entonces los puntos del eje \(y\) que están a \(\sqrt 2 \) del plano \(\pi \) son:
\({P_1}\left( {0,3,0} \right)\) o bien \({P_2}\left( {0, – 1,0} \right)\)

EJERCICIO 3
Calcule el valor del determinante de A matriz de orden 3, sabiendo que \(\left| B \right| = 2\) y \(2{A^2}.{B^{ – 1}} = I\).
Resolución del ejercicio 3
Queremos calcular \(\det \left( A \right)\). Para eso partimos de la expresión:
\[2{A^2}.{B^{ – 1}} = I\]
Los determinantes deben ser iguales:
\[\det \left( {2{A^2}{B^{ – 1}}} \right) = \det \left( I \right)\]
Usando propiedades podemos despejar \(\det \left( A \right)\):
\[ \Rightarrow {2^3}{\left[ {\det \left( A \right)} \right]^2}.\frac{1}{{\det \left( B \right)}} = 1\]
\[ \Rightarrow 8{\left[ {\det \left( A \right)} \right]^2}.\frac{1}{2} = 1\]
\[ \Rightarrow {\left[ {\det \left( A \right)} \right]^2} = \frac{1}{4}\]
\[ \Rightarrow \left| {\det \left( A \right)} \right| = \frac{1}{2}\]
\[ \Rightarrow \det \left( A \right) = \frac{1}{2}{\rm{\;\;\;\;\;}}o{\rm{\;}}bien{\rm{\;\;\;\;}}\det \left( A \right) = – \frac{1}{2}\]
Las propiedades usadas fueron:
\[\det \left( {k.A} \right) = {k^n}\det \left( A \right)\]
\[\det \left( {A.B} \right) = \det \left( A \right).\det \left( B \right)\]
\[\det \left( {{A^k}} \right) = {\left[ {\det \left( A \right)} \right]^k}\]
\[\det \left( {{B^{ – 1}}} \right) = \frac{1}{{\det \left( B \right)}}\]
EJERCICIO 4
Halle las ecuaciones que definen al subespacio S, una base y su dimensión, siendo \(S = gen\left\{ {x + 1,\;\;{x^2} – 2x,\;\;{x^2} + 2x + 4} \right\} \subset {P_2}\).
Resolución del ejercicio 4
El subespacio \(S\) está definido por un conjunto generador. Queremos definirlo por sus ecuaciones.
Si un vector \(a{x^2} + bx + c\) de \({P_2}\) pertenece a \(S\) debe ser combinación lineal de los vectores del conjunto generador:
\[a{x^2} + bx + c = \alpha \left( {x + 1} \right) + \beta \left( {{x^2} – 2x} \right) + \gamma \left( {{x^2} + 2x + 4} \right)\]
Distribuyendo y reagrupando:
\[a{x^2} + bx + c = \left( {\beta + \gamma } \right){x^2} + \left( {\alpha – 2\beta + 2\gamma } \right)x + \left( {\alpha + 4\gamma } \right)\]
Dos polinomios son iguales si sus respectivos coeficientes son iguales:
\[\left\{ {\begin{array}{*{20}{c}}{\beta + \gamma = a}\\{\alpha – 2\beta + 2\gamma = b}\\{\alpha + 4\gamma = c}\end{array}} \right.\]
Usemos el método de eliminación de Gauss para hallar la o las ecuaciones de \(S\):
\[\left( {\begin{array}{*{20}{c}}0&1&1& \vdots &a\\1&{ – 2}&2& \vdots &b\\1&0&4& \vdots &c\end{array}} \right)\mathop \to \limits_{{F_3} – {F_2}} \left( {\begin{array}{*{20}{c}}0&1&1& \vdots &a\\1&{ – 2}&2& \vdots &b\\0&2&2& \vdots &{c – b}\end{array}} \right)\mathop \to \limits_{{F_3} – 2{F_1}} \left( {\begin{array}{*{20}{c}}0&1&1& \vdots &a\\1&{ – 2}&2& \vdots &b\\0&0&0& \vdots &{c – b – 2a}\end{array}} \right)\]
Entonces para los vectores de \(S\) debe cumplirse la igualdad:
\[c – b – 2a = 0\]
\[S = \left\{ {a{x^2} + bx + c \in {P_2}\;|\;c – b – 2a = 0} \right\}\]
\({P_2}\) es un espacio vectorial de dimensión 3. Cómo se obtiene una única ecuación (una única restricción) que define a \(S \subset {P_2}\), entonces \(S\) debe tener dimensión \(2\) (una base de \(S\) tiene dos vectores).
Pero el conjunto generador de \(S\) tiene tres vectores. Tenemos que eliminar a uno de ellos. Por ejemplo, podemos ver que el tercer vector del conjunto generador de S es combinación lineal de los primeros dos:
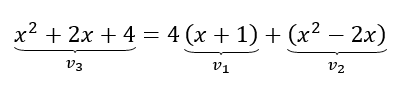
También es \({v_2}\) combinación lineal de \({v_1}\) y \({v_3}\), y \({v_1}\) combinación lineal de \({v_2}\) y \({v_3}\). Hay que quitar a alguno de esos vectores (cualquiera de los tres).
Entonces una base de \(S\) puede ser:
\[{B_S} = \left\{ {x + 1,{x^2} – 2x} \right\}\]
\[\dim \left( S \right) = 2\]
EJERCICIO 5
Dados los subespacios
\({S_1} = \left\{ {\left( {\begin{array}{*{20}{c}}a&b\\c&d\end{array}} \right) \in {\mathbb{R}^{2 \times 2}}\;\;|\;\;\;4a + b + kc = 0} \right\}\) y \({S_1} = \left\{ {\left( {\begin{array}{*{20}{c}}a&b\\c&d\end{array}} \right) \in {\mathbb{R}^{2 \times 2}}\;\;|\;\;\;a + b + c – 3d = 0 \wedge a + d = 0} \right\}\)
a) Halle \(k\), si existe, para que \(\dim \left( {{S_1} \cap {S_2}} \right) = 2\)
b) Para \(k = 1\), halle una base de \({S_1} \cap {S_2}\).
Resolución del ejercicio 5
Ítem a
\({\mathbb{R}^{2 \times 2}}\) es un espacio vectorial de dimensión 4. Para que \({S_1} \cap {S_2}\) tenga dimensión 2, tiene que tener sólo dos ecuaciones/restricciones. Veamos cuánto debe valer \(k\) para que \({S_1} \cap {S_2}\) esté definido por dos ecuaciones.
Los vectores del subespacio \({S_1} \cap {S_2}\) deben cumplir las ecuaciones de \({S_1}\) y también las de \({S_2}\):
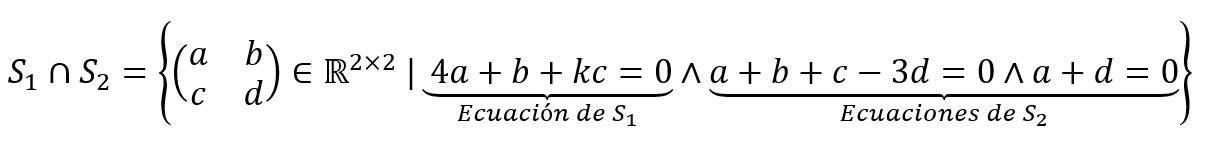
Escribamos a las tres ecuaciones ordenadamente y completando coeficientes para analizar si acaso alguna de esas ecuaciones es redundante:
\[\left\{ {\begin{array}{*{20}{c}}{4a + b + kc + 0d = 0}\\{a + b + c – 3d = 0}\\{a + 0b + 0c + d = 0}\end{array}} \right.\]
Podemos analizarlo más fácilmente escribiendo la matriz ampliada y realizando operaciones elementales entre filas:
\[\left( {\begin{array}{*{20}{c}}4&1&k&0& \vdots &0\\1&1&1&{ – 3}& \vdots &0\\1&0&0&1& \vdots &0\end{array}} \right)\mathop \to \limits_{{F_3} \leftrightarrow {F_1}} \left( {\begin{array}{*{20}{c}}1&0&0&1& \vdots &0\\1&1&1&{ – 3}& \vdots &0\\4&1&k&0& \vdots &0\end{array}} \right)\]
\[\mathop \to \limits_{\begin{array}{*{20}{c}}{{F_2} – {F_1}}\\{{F_3} – 4{F_1}}\end{array}} \left( {\begin{array}{*{20}{c}}1&0&0&1& \vdots &0\\0&1&1&{ – 4}& \vdots &0\\0&1&k&{ – 4}& \vdots &0\end{array}} \right)\mathop \to \limits_{{F_3} – {F_2}} \left( {\begin{array}{*{20}{c}}1&0&0&1& \vdots &0\\0&1&1&{ – 4}& \vdots &0\\0&0&{k – 1}&0& \vdots &0\end{array}} \right)\]
\[\left\{ {\begin{array}{*{20}{c}}{1a + 0b + 0c + 1d = 0}\\{0a + 1b + 1c – 4d = 0}\\{0a + 0b + \left( {k – 1} \right)c + 0d = 0}\end{array}} \right.\]
Para que se elimine la tercera ecuación y queden sólo dos ecuaciones que definan al subespacio, debe ser:
\[k – 1 = 0\]
\[ \Rightarrow k = 1\]
Con \(k = 1\), la dimensión de \({S_1} \cap {S_2}\) es \(2\).
Ítem b
Si \(k = 1\) las ecuaciones son (las leemos desde la versión simplificada obtenida con operaciones elementales de filas):
\[\left\{ {\begin{array}{*{20}{c}}{a + d = 0}\\{b + c–4d = 0}\end{array}} \right.\;\; \Rightarrow \;\left\{ {\begin{array}{*{20}{c}}{a = – d}\\{b = 4d – c}\end{array}} \right.\]
Entonces una matriz de \({S_1} \cap {S_2}\) es de la forma:
\[\left( {\begin{array}{*{20}{c}}{–d}&{4d – c}\\c&d\end{array}} \right)\]
Podemos expresarla así:
\[\left( {\begin{array}{*{20}{c}}{–d}&{4d – c}\\c&d\end{array}} \right) = c\left( {\begin{array}{*{20}{c}}0&{–1}\\1&0\end{array}} \right) + d\left( {\begin{array}{*{20}{c}}{–1}&4\\0&1\end{array}} \right)\]
Luego una base es:
\[{B_{{S_1} \cap {{\rm{S}}_2}}} = \left\{ {\left( {\begin{array}{*{20}{c}}0&{–1}\\1&0\end{array}} \right),\left( {\begin{array}{*{20}{c}}{–1}&4\\0&1\end{array}} \right)} \right\}\]

