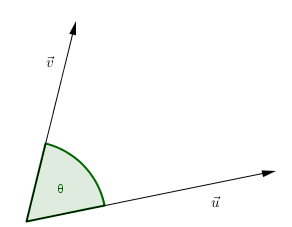
Producto escalar en \({\mathbb{R}^3}\)
Sean \(\vec u\;,\;\vec v \in {\mathbb{R}^3}\), y \(\theta \) el ángulo entre \(\vec u\) y \(\vec v\), entonces el producto escalar entre \(\vec u\) y \(\vec v\) se define como sigue:
Ejemplo
Hallar \(\vec u.\vec v\) para \(\vec u = \left( {0,0,1} \right)\;,\;\vec v = \left( {0,3, – 3} \right)\)
Resolución
Hagamos una gráfica para visualizar el ángulo entre los dos vectores:
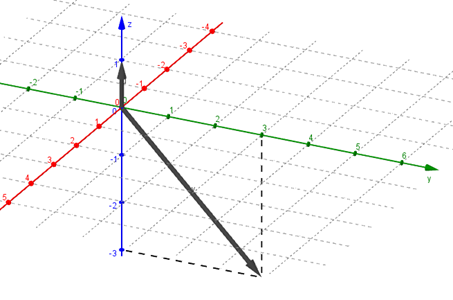
Calculemos los módulos de \(\vec u\). y \(\vec v\):
\[\lVert \vec u\rVert = 1\]
\[\lVert \vec v\rVert = \sqrt {{3^2} + {{\left( { – 3} \right)}^2}} = \sqrt {18} = 3\sqrt 2 \;\;\]
A partir del gráfico podemos determinar que el ángulo entre los vectores es \(\theta = 135^\circ \), o en radianes: \(\theta = \frac{3}{4}\pi \).
Calculemos el producto escalar:
\[\vec u.\vec v = 1.\sqrt {18} .\cos \left( {135^\circ } \right) = 3\sqrt 2 .\left( { – \frac{{\sqrt 2 }}{2}} \right) = – 3\]
Pero no siempre es tan sencillo. Consideremos los vectores:
\[\vec u = \left( { – 3,5,8} \right)\;\;\;\;\;,\;\;\;\;\;\;\vec v\; = \left( {1,1,1} \right)\]
Si quisiéramos calcular el producto escalar entre \(\vec u\) y \(\vec v\), deberíamos conocer el ángulo comprendido entre dichos vectores.
Usando el teorema del coseno se puede deducir otra fórmula para calcular el producto escalar en función de las componentes de los vectores.
Sean \(\vec u = \left( {{u_x},{u_y},{u_z}} \right)\;,\;\;\vec v = \left( {{v_x},{v_y},{v_z}} \right) \in {\mathbb{R}^3}\), entonces:
Para los vectores dados, resulta:
\[\vec u\;.\vec v\; = \;\left( { – 3} \right).1\; + \;5\;.1\; + \;8.1\; = \;10\]
Propiedades del producto escalar
1) \(\vec u.\vec v\; = \;\vec v.\vec u\)
2) \(\vec u.\left( {\vec v\; + \;\vec w} \right)\; = \;\vec u.\vec v\; + \;\vec u.\vec w\)
3) \(k\;\left( {\vec u.\vec v} \right) = \;\left( {k\vec u.\vec v} \right) = \;\vec u.\left( {k\vec v} \right)\;,\;k \in \mathbb{R}\)
4) \(\vec v.\vec v\; = \;\left( {{v_x},{v_y},{v_z}} \right).\;\left( {{v_x},{v_y},{v_z}} \right) = v_x^2 + v_y^2 + v_z^2 = {\lVert \vec v\rVert^2} > 0\;\forall \vec v \ne \vec 0\)
De (4) se deduce que: \(\lVert \vec v\rVert = \sqrt {\vec v.\vec v} \)
Ángulo entre vectores
Dados \(\vec u,\overrightarrow {\;v} \) vectores no nulos de \({\mathbb{R}^3}\), queremos hallar el ángulo entre ellos.
Si \(\theta \) es el ángulo entre \(\vec u\;\;y\;\;\vec v\), de las definiciones [1] y [2] de producto escalar resulta:
\[\cos \left( \theta \right) = \left( {\frac{{\vec u.\vec v}}{{\lVert \vec u\rVert \lVert \vec v\rVert}}} \right)\]
Por ejemplo, si \[\vec u = \left( {1,1,3} \right)\]
\[\vec v = \left( { – 1,0,4} \right)\;\]
\[\theta = \arccos \left( {\frac{{1.\left( { – 1} \right) + 1.0 + 3.4}}{{\sqrt {{1^2} + {1^2} + {3^2}} .\sqrt {{{\left( { – 1} \right)}^2} + {0^2} + {4^2}} \;\;}}} \right)\]
\[\theta = \arccos \left( {\frac{{11}}{{\sqrt {11} .\sqrt {17} \;\;}}} \right) \cong 36,44^\circ \]
Condición de perpendicularidad entre vectores
Sean \(\vec u\;,\;\vec v\) no nulos,
\[\vec u.\vec v = 0 \Leftrightarrow \;\cos \left( \theta \right) = 0 \Leftrightarrow \theta = \frac{\pi }{2}\;\]
Esto permite enunciar una condición de perpendicularidad:
Ejercicio para el lector 1
Dados \(\vec u = \left( {1,2,3} \right)\;\;\;\)y \(\;\;\vec v = \left( {0,2,5} \right)\;\;\)encontrar todos los vectores perpendiculares a \(\vec u\) y a \(\vec v\) de módulo 3.
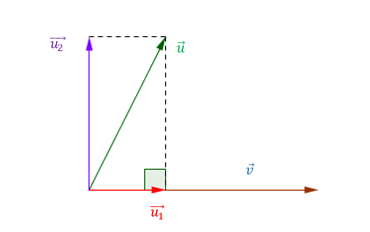
Proyección de un vector en la dirección de otro
El producto escalar es útil en problemas en los que se tiene interés en descomponer un vector como suma de vectores perpendiculares.
Dados dos vectores no nulos \(\vec u\) y \(\vec v\) , nos proponemos descomponer \(\vec u\) como suma de un vector paralelo a \(\vec v\;\;\)y otro perpendicular a \(\vec v.\;\) O sea:
\(\vec u = \overrightarrow {{u_1}} + \overrightarrow {{u_2}} \) , \(\overrightarrow {{u_1}} \parallel \vec v\;\) y \(\;\overrightarrow {\;{u_2}} \bot \vec v\)
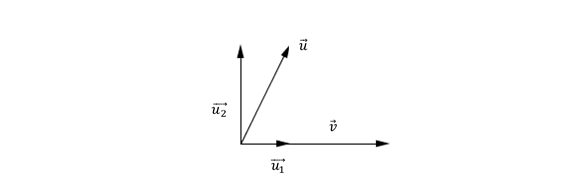
\[\overrightarrow {{u_1}} \parallel \vec v\; \Leftrightarrow \;\;\overrightarrow {{u_1}} = k\vec v\;\;,\;k \in \mathbb{R}\;\;\; \Rightarrow \;\;\vec u = k\vec v + \overrightarrow {{u_2}} \]
Podemos aplicar a ambos miembros producto escalar por \(\vec v\). Teniendo en cuenta que \(\overrightarrow {{u_2}} .\vec v = 0\) por ser perpendiculares, resulta:
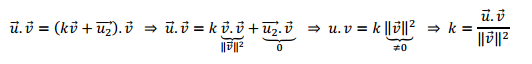
Entonces:
\[\overrightarrow {{u_1}} = \left( {\frac{{\vec u.\vec v}}{{{\lVert \vec v\rVert^2}}}} \right)\vec v\]
Este vector es la proyección de\(\;\vec u\;\)en la dirección de\(\;\vec v\) :
El vector \({\vec u_2}\;\) puede obtenerse por diferencia:
\[\vec u = \overrightarrow {{u_1}} + \overrightarrow {{u_2}} \;\; \Rightarrow \;\overrightarrow {{u_2}} = \vec u – \overrightarrow {{u_1}} \]
Recordemos que \(\overrightarrow {{u_2}} \) debe ser perpendicular a \(\;\vec v\).
Para resolver algunos problemas geométricos, es útil calcular el módulo del vector de proyección:
\[\lVert {\overrightarrow {proy} _{\vec v}}\left( {\vec u} \right)\rVert = \left| {\frac{{\vec u.\vec v}}{{{\lVert \vec v \rVert^2}}}} \right|\ \lVert \vec v \rVert = \frac{{\left| {\vec u.\vec v} \right|}}{{{\lVert \vec v \rVert^2}}}\;\lVert \vec v \rVert\; = \;\frac{{\left| {\vec u.\vec v} \right|}}{{\lVert \vec v \rVert}}\]
Ejemplo
Descomponer \(\vec u = \left( {1,2,1} \right)\) como suma de un vector paralelo a \(\vec v = \left( {0,1, – 1} \right)\) más otro perpendicular a \(\vec v\).
Primero buscamos \(\overrightarrow {{u_1}} \) :
\[\overrightarrow {{u_1}} = {\overrightarrow {proy} _{\vec v}}\left( {\vec u} \right) = \left( {\frac{{\vec u.\vec v}}{{{{\lVert \vec v\rVert}^2}}}} \right)\vec v = \left( {\frac{{\left( {1,2,1} \right).\left( {0,1, – 1} \right)}}{{{0^2} + {1^2} + {{\left( { – 1} \right)}^2}}}} \right)\left( {0,1, – 1} \right)\]
\[ = \frac{{0 + 2 – 1}}{2}\;\left( {0,1, – 1} \right) = \left( {0,\;\frac{1}{{\;2}}, – \frac{1}{2}} \right)\]
\[\overrightarrow {{u_2}} = \vec u – \overrightarrow {{u_1}} = \left( {1,2,1} \right) – \left( {0,\;\frac{1}{{\;2}}, – \frac{1}{2}} \right) = \left( {1,\;\frac{3}{2},\frac{3}{2}} \right)\]
Comprobación: \(\;\;\overrightarrow {{u_2}} \bot \vec v\)
\[\left( {1,\;\frac{3}{2},\frac{3}{2}} \right).\left( {0,1, – 1} \right) = 0\]

