Ecuaciones de la recta en R3
Sabemos que una recta en \({\mathbb{R}^2}\) puede expresarse por la ecuación:
\[y = ax + b\]
Pero ¿qué representa esta ecuación en \({\mathbb{R}^3}\)? En \({\mathbb{R}^3}\) es un plano paralelo al eje \(z\), y en \({\mathbb{R}^2}\) es una recta:
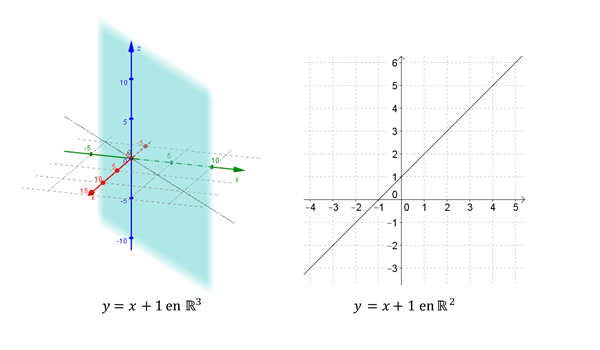
Para definir un plano es suficiente conocer un vector perpendicular al plano y un punto del mismo. ¿Qué datos permiten definir una recta en \({\mathbb{R}^3}\)?
Para definir en forma vectorial una recta en \({\mathbb{R}^3}\), es suficiente conocer un punto de la recta y un vector director que indique la dirección de la misma, o sea un vector paralelo a la recta.
Ecuación vectorial de la recta
Dados un vector \(\vec v = \left( {{v_1},{v_2},{v_3}} \right)\) y un punto \({P_0}\left( {{x_0},{y_0},{z_0}} \right)\), nos proponemos hallar la ecuación de la recta \(r\) que pasa por el punto \({P_0}\) y es paralela al vector \(\vec v\).
Consideremos un punto \(P\left( {x,y,z} \right)\) perteneciente a la recta r. El vector \(\overrightarrow {{P_0}P} \;\) resultará paralelo al vector director \(\vec v\):
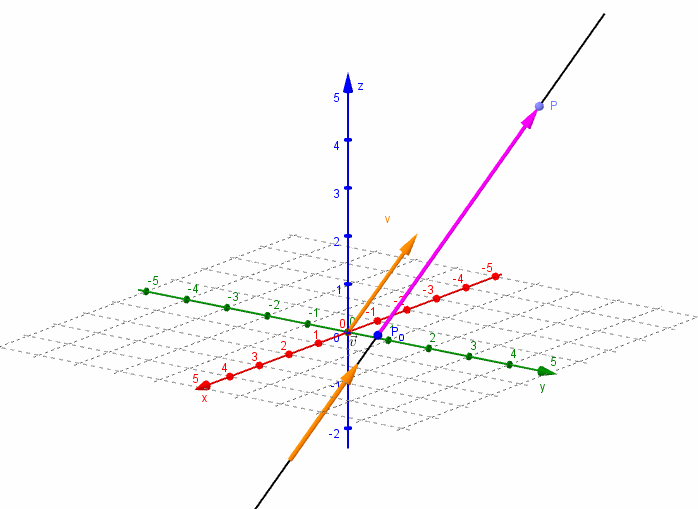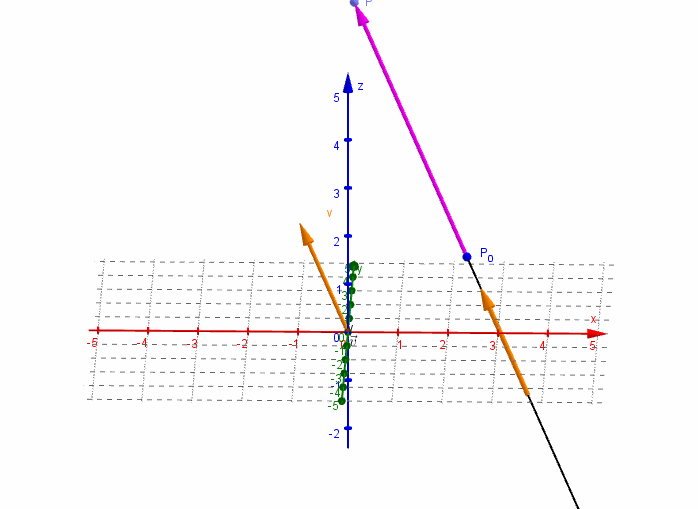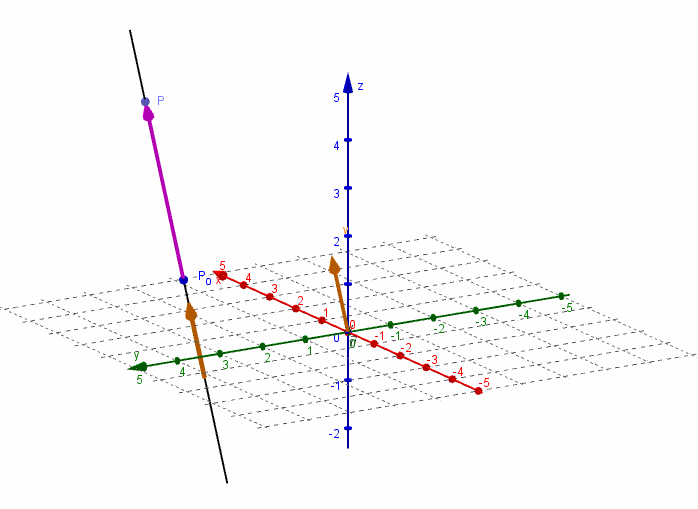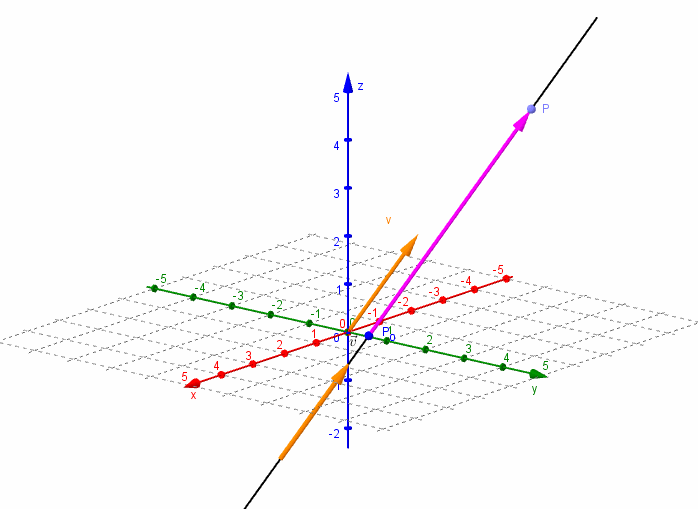
\[\overrightarrow {{P_0}P} = \alpha \vec v\]
\[\left( {x – {x_0},y – {y_0},z – {z_0}} \right) = \alpha \left( {{v_1},{v_2},{v_3}} \right)\]
Ejemplo
Hallar la ecuación vectorial de la recta que pasa por los puntos \(M\left( {3,2,1} \right)\) y \(S\left( { – 1,1,0} \right)\).
Tenemos como datos dos puntos de la recta, entonces los vectores \(\overrightarrow {MS} \) y \(\overrightarrow {SM} \) son paralelos a dicha recta. Elegimos uno de ellos como vector director:
\[\vec v = \overrightarrow {MS} = \left( { – 4, – 1, – 1} \right)\]
Podemos tomar cualquiera de los dos puntos dados cómo punto de paso, por ejemplo \(M\). Entonces la ecuación es:
\[\left( {x,y,z} \right) = \left( {3,2,1} \right) + \alpha \left( { – 4, – 1, – 1} \right)\;\;\;,\;\;\;\alpha \in \mathbb{R}\;\;\;\;\;ecuació n\;vectorial\;de\;la\;recta\;MS\]
Para cada valor de \(\alpha \in \mathbb{R}\;,\;\)se obtiene un punto de la recta. Por ejemplo, si \(\alpha = \; – 1\) se obtiene el punto \({P_1}\left( {7,3,2} \right) \in r.\)
¿\(\left( {5, – 3,1} \right) \in r\;\)?
Veamos si existe algún valor de \(\alpha \) que verifique esta ecuación vectorial:
\[\left( {5, – 3,1} \right) = \left( {3,2,1} \right) + \alpha \left( { – 4, – 1, – 1} \right)\]
\[\left\{ {\begin{array}{*{20}{c}}{3 – 4\alpha = 5}\\{2 – \alpha = – 3}\\{1 – \alpha = 1}\end{array}} \right.\;\]
Este sistema es incompatible, así que el punto no pertenece a la recta.
¿Para qué valor de \(\alpha \) se obtiene el punto \(S\)?
Ecuaciones paramétricas de la recta
Hemos visto que la ecuación vectorial de una recta es:
\[\left( {x,y,z} \right) = \left( {{x_0},{y_0},{z_0}} \right) + \alpha \left( {{v_1},{v_2},{v_3}} \right)\]
Por igualdad de vectores:
\(\left\{ {\begin{array}{*{20}{c}}{x = {x_0} + \alpha \;{v_1}}\\{y = {y_0} + \alpha \;{v_2}}\\{z = {z_0} + \alpha \;{v_3}}\end{array}} \right.\) \(\alpha \in \mathbb{R}\)
Éstas son las ecuaciones cartesianas paramétricas de la recta.
Ecuaciones simétricas de la recta
Si \(\;{v_1},{v_2},{v_3}\;\) son distintos de cero, entonces:
\[\alpha = \frac{{x – {x_o}}}{{{v_1}}}\;\;\;,\;\;\;\;\alpha = \frac{{y – {y_o}}}{{{v_2}}}\;\;\;\;\;,\;\;\;\;\alpha = \frac{{z – {z_o}}}{{{v_3}}}\]
Igualando, resulta:
\[\frac{{x – {x_o}}}{{{v_1}}} = \frac{{y – {y_o}}}{{{v_2}}} = \frac{{z – {z_o}}}{{{v_3}}}\;\;\;\;\;\;\;\;Ecuaciones\;simé tricas\;de\;la\;recta\]
Ejemplo
Consideremos la ecuación vectorial de la recta \(MS\):
\[\left( {x,y,z} \right) = \left( {3,2,1} \right) + \alpha \left( { – 4, – 1, – 1} \right)\;\;\;,\;\;\;\alpha \in \mathbb{R}\;\]
¿Cómo podemos obtener las ecuaciones paramétricas de la recta? Simplemente por igualdad de vectores escribimos:
\[\left\{ {\begin{array}{*{20}{c}}{x = 3 – 4\alpha }\\{y = 2 – \alpha }\\{z = 1 – \alpha }\end{array}} \right.\;\;\alpha \in \mathbb{R}\;\;\;\;\;\;,\;\;\;\;\;\;Ecuaciones\;paramé tricas\;de\;la\;recta\;MS\]
Para obtener las ecuaciones simétricas, despejamos el parámetro e igualamos:
\[\alpha = \frac{{x – 3}}{{ – 4}}\;\;,\;\;\;\alpha = \frac{{y – 2}}{{ – 1}}\;\;,\;\;\alpha = \frac{{z – 1}}{{ – 1}}\]
\[\frac{{x – 3}}{4} = y – 2 = z – 1\;\;\;\;\;\;\;,\;\;\;Ecuaciones\;simé tricas\;de\;la\;recta\;MS\]
Recta definida como intersección de dos planos
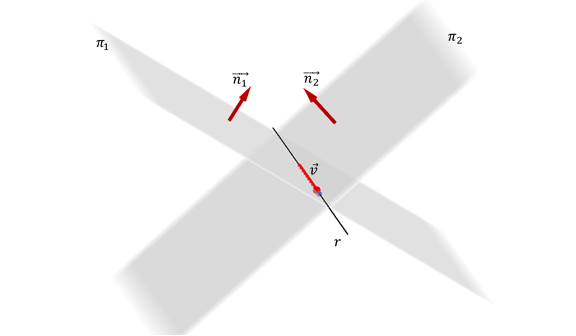
Dos planos no paralelos \(\;{\pi _{1\;}}:\;{a_1}x + {b_1}y + {c_1}z + {d_1} = 0\) y \({\pi _2}\;:\;{a_2}x + {b_2}y + {c_2}z + {d_2} = 0\) determinan al cortarse una recta en R3 que queda expresada por el sistema de ecuaciones lineales:
\[r:\;\;\left\{ {\begin{array}{*{20}{c}}{\;{a_1}x + {b_1}y + {c_1}z + {d_1} = 0}\\{\;{a_2}x + {b_2}y + {c_2}z + {d_2} = 0}\end{array}} \right.\;\]
Ejemplo
Consideremos el siguiente ejemplo:
\[r:\;\left\{ {\begin{array}{*{20}{c}}{\;x + y + z + 1 = 0\;\;\;\;\;\;\;\;{\pi _1}}\\{\;x – y – z + 2 = 0\;\;\;\;\;\;\;\;{\pi _2}}\end{array}} \right.\]
Éste es un sistema de \(2\;x\;3\) (de 2 ecuaciones con 3 incógnitas) cuyo conjunto solución es la recta \(r\).
¿Cómo podemos hallar un vector director de la recta y un punto de la misma?
Para obtener \(\vec v\) , debe tenerse en cuenta que:
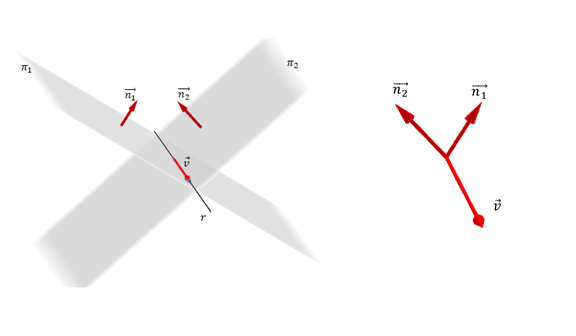
Por lo tanto \(\overrightarrow {{n_1}} \; \times \overrightarrow {{n_2}} \;\) es un vector paralelo a \(r\). Así encontramos un vector director de \(r\):
\[\vec v = \overrightarrow {{n_1}} \; \times \overrightarrow {{n_2}} = \left( {0,2, – 2} \right)\]
Para hallar un punto \({P_0} \in r\) , podemos fijar el valor de una de las variables en el sistema de ecuaciones que define a la recta, por ejemplo fijemos arbitrariamente \(z\; = \;0\)
Reemplazando en el sistema, nos queda:
\[\left\{ {\begin{array}{*{20}{c}}{\;x + y + 1 = 0\;\;\;\;\;\;\;\;}\\{\;x – y + 2 = 0\;\;\;\;\;\;\;\;}\end{array}} \right.sistema\;2×2\]
Resolviendo este sistema, obtenemos: \(x = – \;\frac{3}{2}\;\;\;,\;\;\;y = \;\frac{1}{2}\) por lo cual un punto de la recta es \({P_0}\left( { – \;\frac{3}{2}\;,\;\frac{1}{2},0} \right)\).
Con la información obtenida, estamos en condiciones de escribir la ecuación vectorial de la recta:
\[r:\left( {x,y,z} \right) = \left( { – \;\frac{3}{2}\;,\;\frac{1}{2},0} \right) + \lambda \left( {0,2, – 2} \right)\;\;\;,\;\;\;\lambda \; \in R\]
Observación: Si para buscar un punto de la recta fijáramos \(x\; = \;0\) (en lugar de \(z\; = \;0\)), nos quedaría el siguiente sistema: \(\left\{ {\begin{array}{*{20}{c}}{y + z + 1 = 0\;\;\;\;\;\;\;\;}\\{\; – y – z + 2 = 0\;\;\;\;\;\;\;\;}\end{array}} \right.\)que es incompatible.
¿Por qué se produce esta incompatibilidad? Porque no hay ningún punto de la recta en el plano \(x\; = \;0\), o sea la recta no interseca al plano \(x = 0\).
En resumen:
Dada una recta \(r:\;\;\left\{ {\begin{array}{*{20}{c}}{\;{a_1}x + {b_1}y + {c_1}z + {d_1} = 0}\\{\;{a_2}x + {b_2}y + {c_2}z + {d_2} = 0}\end{array}} \right.\;\;\;\;\)
podemos obtener un vector director calculando el producto vectorial \(\overrightarrow {{n_1}} \; \times \overrightarrow {{n_2}} \) .
Para obtener un punto de la recta, fijamos arbitrariamente el valor de una de las variables y resolvemos el sistema 2×2 resultante.
Ejemplo
Retomemos el ejemplo anterior:
\[r:\;\left\{ {\begin{array}{*{20}{c}}{\;x + y + z + 1 = 0\;\;\;\;\;\;\;\;{\pi _1}}\\{\;x – y – z + 2 = 0\;\;\;\;\;\;\;\;{\pi _2}}\end{array}} \right.\]
Otra forma de obtener la ecuación vectorial de la recta es resolver el sistema de ecuaciones que la define.
Escribimos la matriz ampliada asociada al sistema:
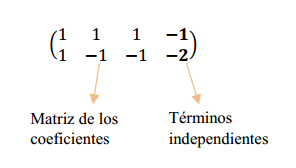
Aplicamos operaciones elementales entre filas para resolver el sistema de ecuaciones:
\[\left( {\begin{array}{*{20}{c}}1&1&1&{ – 1}\\1&{ – 1}&{ – 1}&{ – 2}\end{array}} \right)\mathop \to \limits_{{F_2} \to \;{F_2} – {F_1}} \left( {\begin{array}{*{20}{c}}1&1&1&{ – 1}\\0&{ – 2}&{ – 2}&{ – 1}\end{array}} \right)\]
\[\mathop \to \limits_{{F_2} \to \; – \frac{1}{2}{F_2}} \left( {\begin{array}{*{20}{c}}1&1&1&{ – 1}\\0&1&1&{0,5}\end{array}} \right)\mathop \to \limits_{{F_1} \to {F_1} – {F_2}} \left( {\begin{array}{*{20}{c}}1&0&0&{ – 1,5}\\0&1&1&{0,5}\end{array}} \right)\]
\[\left( {\begin{array}{*{20}{c}}1&0&0&{ – 1,5}\\0&1&1&{0,5}\end{array}} \right)\]
Y ahora escribimos el sistema simplificado:
\[\left\{ {\begin{array}{*{20}{c}}{x = – 1,5}\\{y + z = 0,5}\end{array}\;} \right.\]
O sea:
\[\left\{ {\begin{array}{*{20}{c}}{x = – 1,5}\\{y = 0,5 – z}\end{array}\;} \right.\]
Entonces el conjunto solución se puede expresar así:
\[S = \left\{ {\left( {x,y,z} \right) \in {\mathbb{R}^3}\;|\;\;x = – 1,5\;\; \wedge \;\;y = 0,5 – z} \right\}\]
Y podemos escribir la ecuación vectorial de la recta \(r\):
\[\left( {x,y,z} \right) = \left( { – 1,5\;\;;\;\;0,5 – z\;\;;\;\;z} \right)\]
Llamando \(z = \lambda \) , resulta:
\[r:\;\;\left( {x,y,z} \right) = \left( { – 1,5\;;\;0,5\;;0} \right) + \lambda \;\left( {0, – 1,1} \right)\;\;\;,\;\;\;\lambda \in \mathbb{R}\]
Videos con ejercicios resueltos sobre recta en R3

