Enunciado del segundo parcial de álgebra [10-11-2018]

Ejercicio 1
Sea la transformación lineal \(T:{\mathbb{R}^3} \to {\mathbb{R}^3}\) tal que \(M{\left( T \right)_{BE}} = \left( {\begin{array}{*{20}{c}}a&{ – 1}&0\\3&{ – 3a}&1\\0&0&2\end{array}} \right)\), siendo las bases \(B = \left\{ {\left( {2,\;0,\;0} \right),\;\left( {0, – 1,\;0} \right),\;\left( {0,\;0,\;1} \right)} \right\}\) y \(E\) canónica de \({\mathbb{R}^3}\)
a) Hallar los valores de ¿\({\rm{a}} \in \mathbb{R}\) tal que \(\dim Nu\left( T \right) = 1\)?
b) Para \(a = – 1\) analizar justificando si \(\left( { – 4, – 2,\;0} \right) \in Nu\left( T \right)\)
Resolución del ejercicio 1
Resolución en video:
Ejercicio 2
Determinar si las siguientes afirmaciones son V o F. Justificar la respuesta.
a) \(T:V \to V\) es una transformación lineal tal que \(\dim \left( {Nu\left( T \right)} \right) > 1 \Rightarrow T\) es biyectiva
b) \(\alpha \in \mathbb{R}\) es un autovalor de la matriz \(A\) \( \Rightarrow \) el sistema de ecuaciones \(\left( {A – \alpha I} \right)X = 0\) admite sólo la solución trivial.
Resolución del ejercicio 2
Ítem a
Sabemos que \(T\) es una transformación lineal de \(V\) a \(V\). Es decir que el dominio y codominio son el mismo conjunto (y tienen la misma dimensión).
Entonces podemos usar el teorema que afirma que:
Sea \(F:V \to W\) una \(TL\), \(dim\left( V \right) = dim\left( W \right) = n\) Puede afirmarse que: \(F\) es inyectiva ⇔ \(F\) es sobreyectiva ⇔ \(F\) es biyectiva.
Para que sea biyectiva debería ser inyectiva.
Pero por otra parte sabemos que una TL es inyectiva \( \Leftrightarrow \) \(Nu\left( T \right) = \left\{ {{0_V}} \right\}\)
Como \(\dim \left( {Nu\left( T \right)} \right) > 1\),\(\;T\) no es inyectiva, y entonces tampoco es biyectiva.
La afirmación es falsa.
Ítem b
Si \(\alpha \) es autovalor, esto significa que \(\left( {A – \alpha I} \right).X = 0\) es un sistema compatible indeterminado (las infinitas soluciones son los autovectores de \(A\) asociados a \(\alpha \).
La afirmación es falsa.
Que el sistema \(\left( {A – \alpha I} \right).X = 0\) es SCI se basa en la definición de autovalor. Buscamos los infinitos vectores no nulos que se transforman en un múltiplo escalar de sí mismos.
Para más detalle leer la explicación sobre autovalores y autovectores.
Ejercicio 3
Si \(M = \left( {\begin{array}{*{20}{c}}3&1&2\\0&a&0\\1&{ – 1}&2\end{array}} \right)\), hallar los valores de \(a\) para los cuales la matriz \(M\) es diagonalizable.
Resolución ejercicio 3
Recordemos que para determinar si una matriz \(A \in {\mathbb{R}^{n \times n}}\) es diagonalizable debemos determinar si tiene \(n\) autovectores linealmente independientes.
Para eso vamos a hallar sus autovalores. Después analizar el autoespacio asociado a los autovalores. Y de esa forma vamos a saber si se puede o no obtener tres vectores linealmente independientes.
Los autovalores se obtienen resolviendo la ecuación característica de la matriz:
\[det\left( {\begin{array}{*{20}{c}}{3 – \lambda }&1&2\\0&{a – \lambda }&0\\1&{ – 1}&{2 – \lambda }\end{array}} \right) = \left( {3 – \lambda } \right)\left| {\begin{array}{*{20}{c}}{a – \lambda }&0\\{ – 1}&{2 – \lambda }\end{array}} \right| + 1.\left| {\begin{array}{*{20}{c}}1&2\\{a – \lambda }&0\end{array}} \right| = 0\]
\[ = \left( {3 – \lambda } \right)\left( {a – \lambda } \right)\left( {2 – \lambda } \right) + 1.\left( { – 2.\left( {a – \lambda } \right)} \right) = 0\]
\[ = \left( {3 – \lambda } \right)\left( {a – \lambda } \right)\left( {2 – \lambda } \right) + \left( { – 2} \right)\left( {a – \lambda } \right) = 0\]
\[ = \left( {a – \lambda } \right).\left[ {\left( {3 – \lambda } \right)\left( {2 – \lambda } \right) – 2} \right] = 0\]
\[ = \left( {a – \lambda } \right).\left[ {6 – 5\lambda + {\lambda ^2} – 2} \right] = 0\]
\[ = \left( {a – \lambda } \right).\left[ {4 – 5\lambda + {\lambda ^2}} \right] = 0\]
\[ = \left( {a – \lambda } \right).\left( {\lambda – 1} \right).\left( {\lambda – 4} \right) = 0\]
Los autovalores son:
\[\lambda = a \vee \lambda = 1 \vee \lambda = 4\]
Sabemos que autovalores diferentes están asociados a autovectores LI.
Así que si \(a \ne 1 \wedge a \ne 4\), la martiz es diagonalizable.
Pero ¿si \(a = 1\) o si \(a = 4\)? ¿Qué ocurre? Tenemos que analizarlo.
Si \(a = 1\), entonces \(\lambda = 1\) será autovalor doble. Tendremos que analizar la dimensión del autoespacio asociado.
Si \(a = 4\), entonces \(\lambda = 4\) será autovalor doble. Tendremos que analizar la dimensión del autoespacio asociado.
Caso \(a = 1\).
\[Autovectores\;de\;M:\;\;\;1\;\left( {doble} \right)\;\;4\;\left( {simple} \right)\]
Autoespacio asociado a \(\lambda = 1\) (autovalor doble).
\[\left( {\begin{array}{*{20}{c}}2&1&2\\0&0&0\\1&{ – 1}&1\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\{\begin{array}{*{20}{c}}y\\z\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\0\\0\end{array}} \right)\]
La dimensión del autoespacio asociado a \(\lambda = 1\) es igual a 1.
No coinciden dimensión algebraica y geométrica. No se puede hallar tres autovectores LI. No es diagonalizable la matriz para \(a = 1.\)
Caso \(a = 4\).
\[Autovectores\;de\;M:\;\;\;1\;\left( {simple} \right)\;\;4\;\left( {doble} \right)\]
Autoespacio asociado a \(\lambda = 4\) (autovalor doble).
\[\left( {\begin{array}{*{20}{c}}{ – 1}&1&2\\0&0&0\\1&{ – 1}&{ – 2}\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\{\begin{array}{*{20}{c}}y\\z\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\0\\0\end{array}} \right)\]
La dimensión del autoespacio asociado a \(\lambda = 4\) es igual a 2.
Coinciden dimensión algebraica y geométrica. Se puede hallar tres autovectores LI. La matriz M es diagonalizable la matriz para \(a = 4.\)
Ejercicio 4
Sea la ecuación: \({x^2} + A{y^2} + {z^2} – 2z = 0\)
a) Hallar el/los valores de A para los cuales corresponda a una superficie cilíndrica.
b) Para \(A = \frac{1}{4}\) identificar y graficar la superficie. Identifique la intersección de la superficie con el plano \(y = 2\) e identifíquelo en el gráfico.
Resolución del ejercicio 4
Ítem a
La ecuación de una superficie cilíndrica es tal que le “falta” una de las variables.
Por ejemplo:
\({x^2} + {y^2} = 1\;\)Es un cilindro circular con eje paralelo al eje \(z\) (“falta” la letra z en la ecuación).
\({x^2} – {z^2} = 1\) es un cilindro hiperbólico con eje paralelo al eje y (“falta” la letra y en la ecuación).
Considerando esto… la única forma de que la expresión \({x^2} + A{y^2} + {z^2} – 2z = 0\) represente una superficie cilíndrica es que \(A = 0\) para que falte la \(y\) de la ecuación.
Ítem b
Reemplazamos \(A = \frac{1}{4}\) en la ecuación:
\[{x^2} + \frac{1}{4}{y^2} + {z^2} – 2z = 0\]
Completamos cuadrados en \(z\):
\[{x^2} + \frac{1}{4}{y^2} + {z^2} – 2z + 1 – 1 = 0\]
\[{x^2} + \frac{1}{4}{y^2} + {\left( {z – 1} \right)^2} – 1 = 0\]
\[{x^2} + \frac{1}{4}{y^2} + {\left( {z – 1} \right)^2} = 1\]
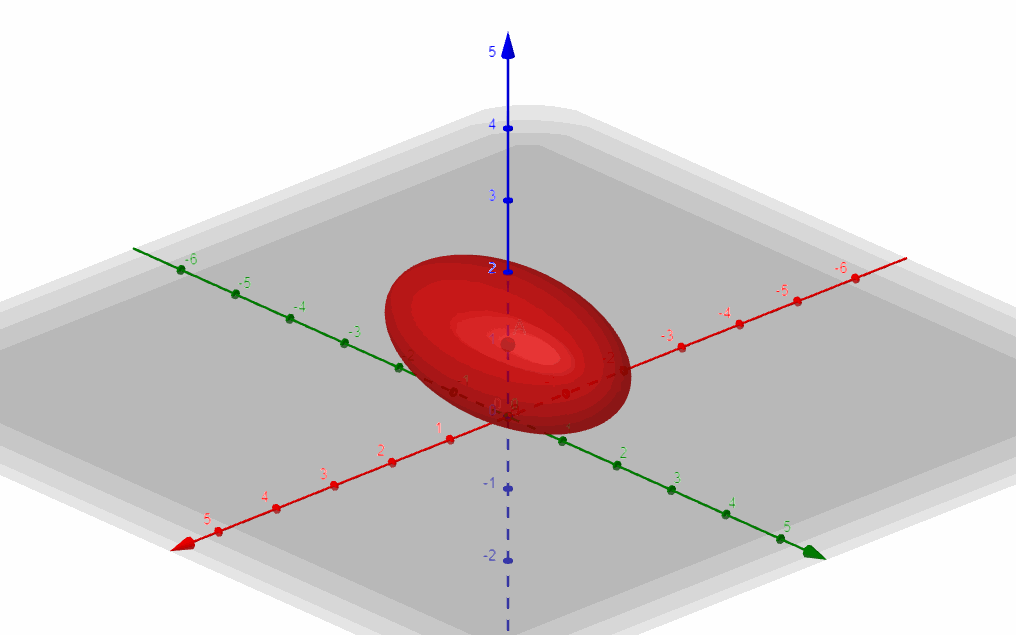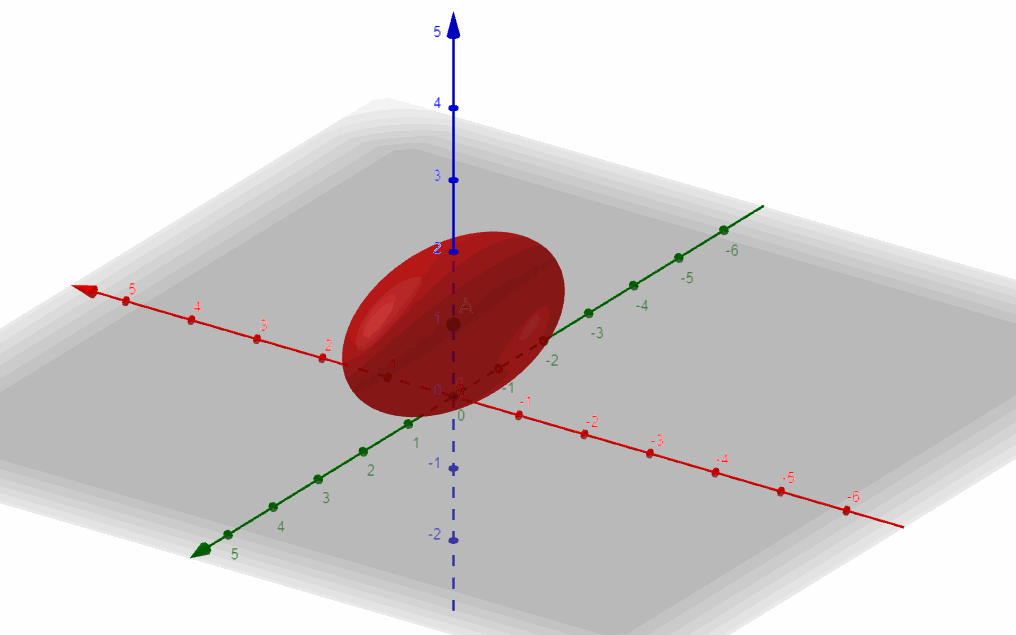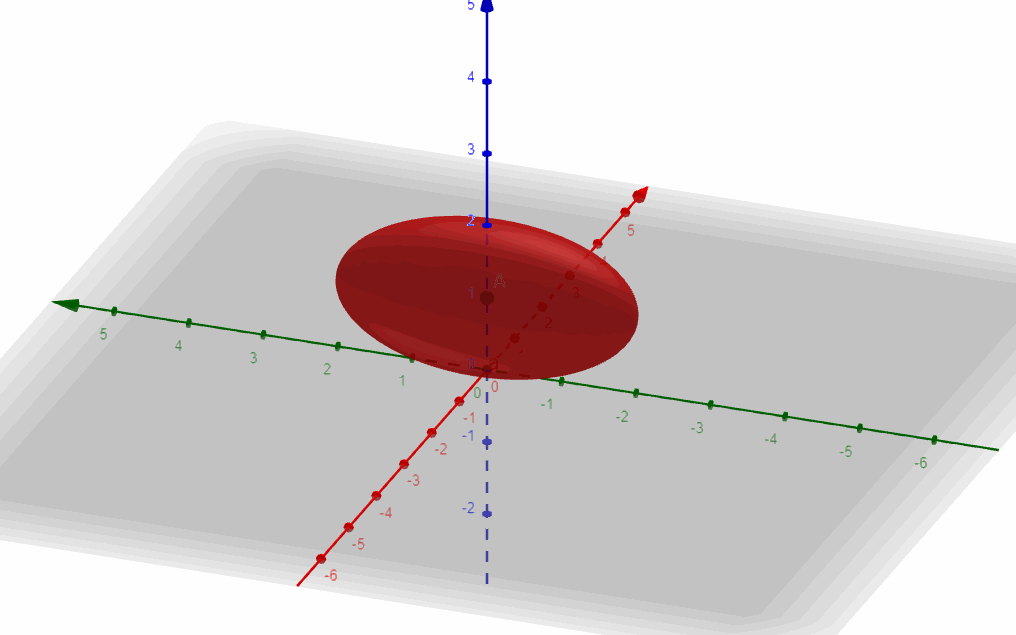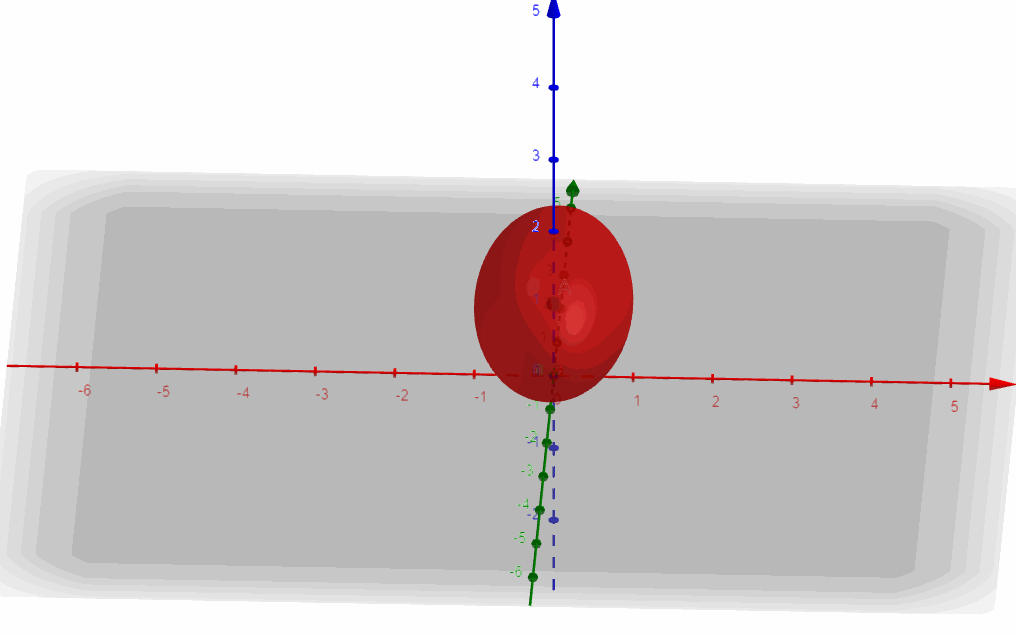
Es la ecuación de un elipsoide centrado en \(\left( {0,0,1} \right)\).
Ejercicio 5
Determinar el conjunto de puntos del plano complejo que satisfacen:
\(\left| {Z – \left( {3 – 4i} \right)} \right| \le 2\) y \(Im\left( Z \right) \le – 4\) \(Z \in \mathbb{C}\)
Representar gráficamente.
Resolución del ejercicio 5
Una forma de pensarlo consiste en:
Escribir a \(z\) en forma binómica:
\[z = x + i.y\]
Identificar su parte real y su parte imaginaria:
\[Re\left( z \right) = Re\left( {x + i.y} \right) = x\]
\[Im\left( z \right) = Im\left( {x + i.y} \right) = y\]
Reemplazar en las condiciones dadas:
\(\left| {x + i.y – \left( {3 – 4i} \right)} \right| \le 2\) y \(y \le – 4\)
Agrupar parte real e imaginaria dentro de la expresión del módulo:
\(\left| {\left( {x – 3} \right) + i.\left( {y + 4} \right)} \right| \le 2\) y \(y \le – 4\)
Calcular el módulo del complejo:
\(\sqrt {{{\left( {x – 3} \right)}^2} + {{\left( {y + 4} \right)}^2}} \le 2\) y \(y \le – 4\)
Elevar al cuadrado a ambos miembros para obtener la ecuación de un círculo:
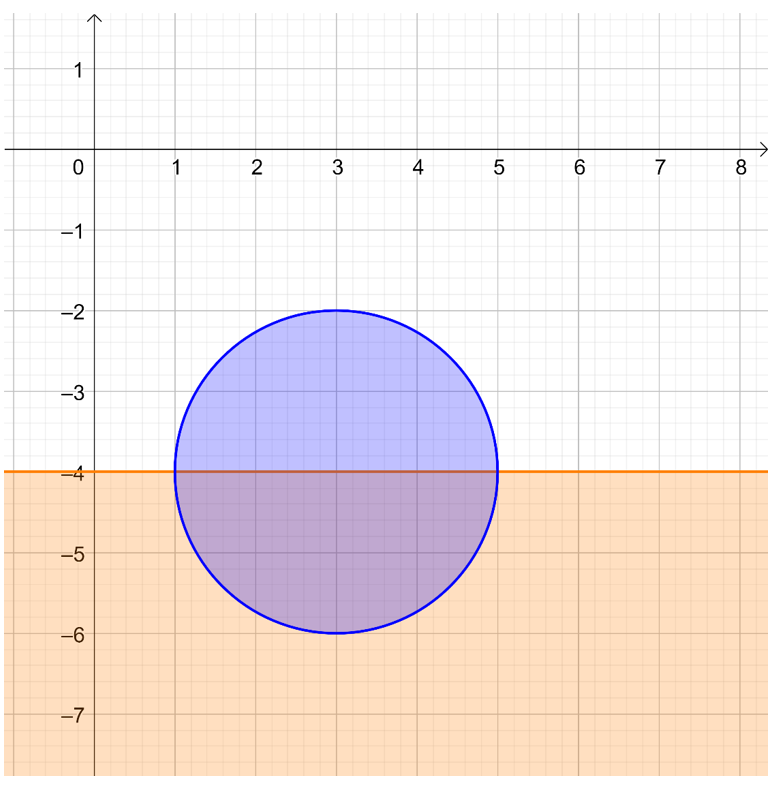
\({\left( {x – 3} \right)^2} + {\left( {y – \left( { – 4} \right)} \right)^2} \le 4\) y \(y \le – 4\)
La expresión \({\left( {x – 3} \right)^2} + {\left( {y – \left( { – 4} \right)} \right)^2} \le 4\) representa un círculo centrado en (3,-4) con radio 2. Incluye el borde y el interior. La expresión \(y \le – 4\) es un semiplano: el de los puntos que tienen parte imaginaria menor a -4. El semiplano de los puntos en los que \(y \le – 4\). Las dos condiciones juntas determinan la mitad de un círculo: